생산적 모델 - 변이형 오토인코더

복습: 오토인코더 (Auto-encoder, AE)

간단히 요약하자면, 매우 단순한 형태의 AE는 다음과 같다:

• 우선, 오토인코더는 값을 입력받고 이를 아핀 변환^{affine transformation}, $\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$ 여기에서 $f$는 (요소별) 활성 함수, 을 통해 은닉 상태^{hidden state}로 매핑한다. 이것이 바로 인코더^encoder 단계이다. 여기서 $\boldsymbol{h}$ 는 코드^code 라고도 불린다.
• 다음으로 $\hat{\boldsymbol{x}} = g(\boldsymbol{W}_x \boldsymbol{h} + \boldsymbol{b}_x)$, 에서 $g$ 는 활성 함수이다. 이것은 디코더^decoder 단계이다.

자세한 설명은, 7 주차 강의 노트를 참조하기 바란다.

변이형 오토인코더^VAE에 관한 직관 및 고전적인 오토인코더와의 비교

다음으로, 생성 모델의 한 유형인 변이형 오토인코더 (또는 VAE)를 소개한다. 그런데 대체 왜 우리는 생성 모델^{generative models}에 관심을 가질까? 이에 대해 답하자면, 판별 모델^{discriminative model}은 주어진 관측에 대해 예측을 하는 것을 배우지만, 생성 모델^{generative model}은 데이터 생성 프로세스를 시뮬레이션 하는 것을 목표로 한다. 한 가지 효과는 생성적 모델이 근본적인 인과 관계를 더 잘 이해하여 더 나은 일반화를 이뤄낼 수 있다는 것이다.

여기서 VAE는 이름에 (오토인코더와의 구조적 혹은 설계적 유사성으로 인해)”오토인코더” (AE) 를 포함하고 있지만, VAE와 AE의 구성에는 큰 차이점이 있다는 것을 알아둘 필요가 있다. 아래의 그림 1 을 참조하기 바란다.

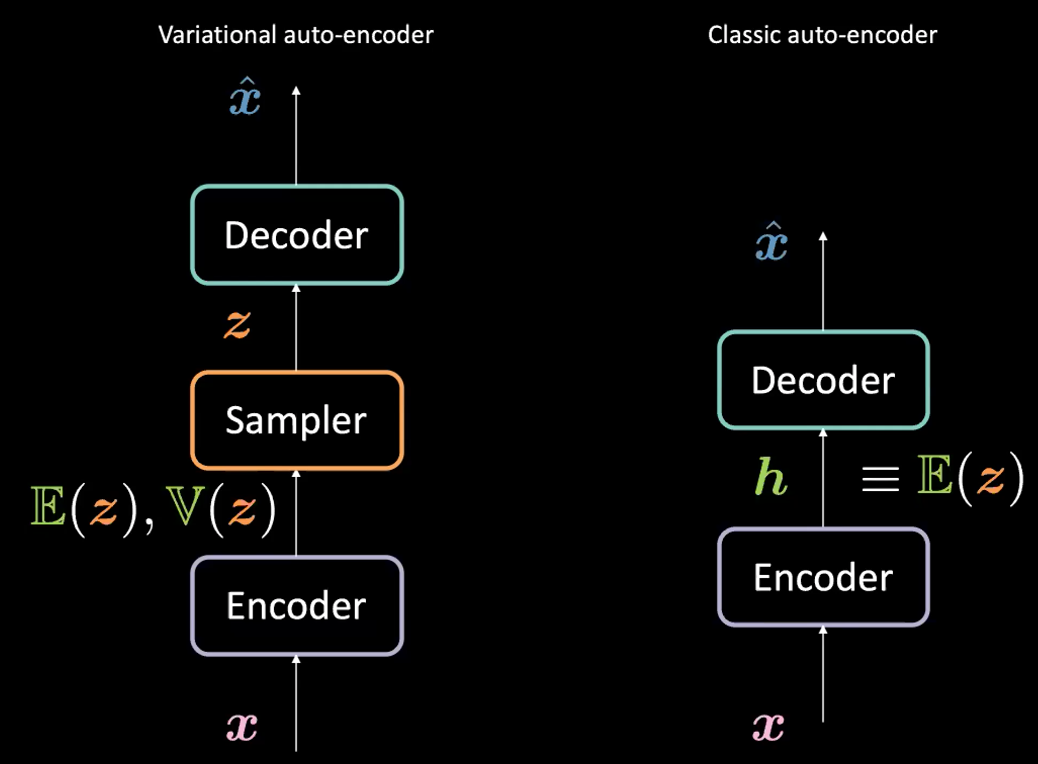
그림. 1: VAE vs. 고전적 AE

변이형 오토인코더 (VAE) 와 고전적인 오토인코더 (AE) 사이의 차이점은 무엇일까?

VAE의 경우:

• 먼저 인코더 단계: $\boldsymbol{x}$ 을 입력으로 인코더에 넘긴다. AE 에서 은닉 표현 $\boldsymbol{h}$ (코드)을 생성하는 대신에, VAE의 코드는 둘로 구성되어 있다: $\mathbb{E}(\boldsymbol{z})$ 와 $\boldsymbol{z}$ 을 잠재 변수로 가지고 평균이 $\mathbb{E}(\boldsymbol{z})$ 이고 분산이 $\mathbb{V}(\boldsymbol{z})$ 인 가우시안 분포를 따르는 $\mathbb{V}(\boldsymbol{z})$. 일반적으로 가우시안 분포를 인코딩된 분포로 사용하지만 다른 분포도 사용될 수 있다.
  • 인코더는 $\mathcal{X}$ 에서 $\mathbb{R}^{2d}$ 로 향하는 함수가 된다: $\boldsymbol{x} \mapsto \boldsymbol{h}$ (여기에서 $\boldsymbol{h}$ 을 $\mathbb{E}(\boldsymbol{z})$ 와 $\mathbb{V}(\boldsymbol{z})$ 의 연결을 나타낸다.)
• 다음으로, 인코더로 매개변수화 된 위의 분포에서 $\boldsymbol{z}$ 을 샘플로 추출한다. 특히, $\mathbb{E}(\boldsymbol{z})$ 와 $\mathbb{V}(\boldsymbol{z})$ 는 잠재 변수 $\boldsymbol{z}$ 를 생성하는 샘플러^sampler 로 전달된다.
• 이 다음, $\boldsymbol{z}$ 가 $\hat{\boldsymbol{x}}$ 을 생성하기 위한 디코더로 전달된다.
  • 이 디코더는 $\mathcal{Z}$ 에서 $\mathbb{R}^{n}$ 로의 함수: $\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$ 이다.

실제로 고전적인 오토인코더의 경우, $\boldsymbol{h}$ 을 VAE 공식 속 벡터 $\E(\boldsymbol{z})$ 로 생각할 수 있다. 즉, VAE와 AE 사이의 주된 차이점은 VAE가 생성 프로세스를 가능하게 하는 좋은 잠재 공간을 가지고 있다는 것이다.

VAE 목적 (손실) 함수

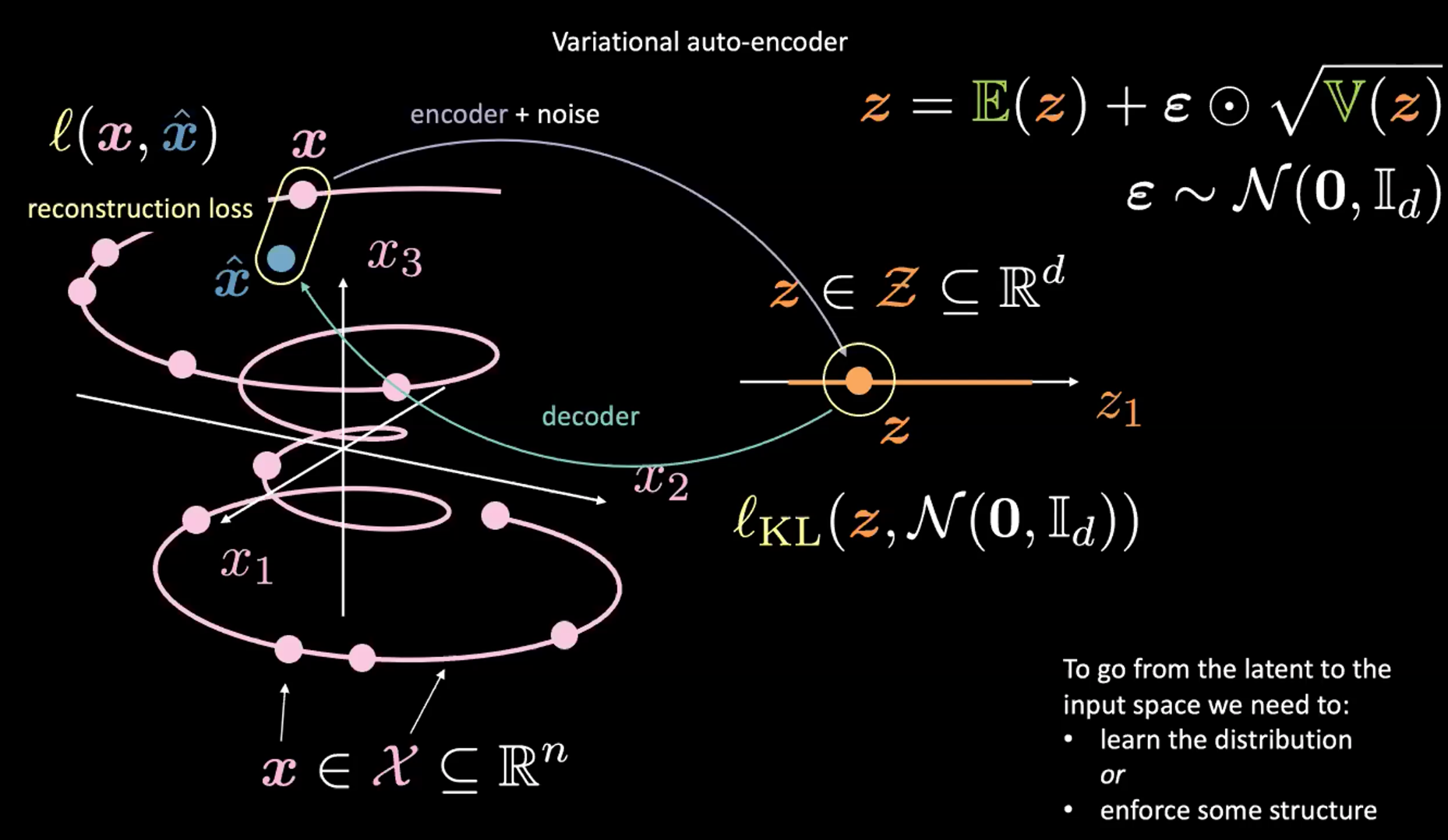
그림. 2: 입력 공간에서 잠재 공간으로의 매핑

위의 그림 2 에서 지금은 오른쪽 상단 모퉁이 부분 (다음 섹션에서 설명할 재매개변수화^{reparameterisation} 트릭^trick) 은 무시하기 바람.

먼저, 인코더와 노이즈를 통해 입력 공간 (왼쪽) 에서 잠재 공간^{latent space</spu> (오른쪽) 으로 인코딩한다. 다음으로 잠재 공간 (오른쪽) 에서 출력 공간 (왼쪽)으로 디코딩한다. 잠재 공간에서 입력 공간으로 가려면 (생성 프로세스), 우리는 (잠재 코드) 분포를 배우거나 어떤 구조를 적용해야 한다. 이 경우에 VAE 는 잠재 공간에 어떤 구조를 적용한다.}

평소처럼 VAE 를 훈련시키기 위해 손실 함수를 최소화한다. 따라서 손실 함수는 재구성^{reconstruction}하는 항과 정규화^{regularization} 하는 항으로 이루어진다.

• 재구성 항은 최종 레이어 (그림의 왼쪽 부분) 에 있다. 이것은 그림에서 $l(\boldsymbol{x}, \hat{\boldsymbol{x}})$ 에 해당한다.
• 정규화 항은 특정한 가우시안 구조를 잠재 공간 (그림의 오른쪽 부분)에 적용하기 위해 잠재 레이어에 위치한다. 이를 위해 벌칙(페널티) 항 $l_{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d))$ 를 사용한다. 이 항이 없으면 VAE 는 고전적인 오토인코더처럼 작동하여 과적합으로 이어질 수 있고, 우리가 원하는 생성 특징을 갖지 못한다.

샘플링 $\boldsymbol{z}$ 에 대한 논의(재매개변수화 트릭^{reparameterisation trick})

VAE 의 인코더가 내놓은 분포를 어떻게 샘플링 해야 할까? 위의 내용에 따르면, $\boldsymbol{z}$ 를 얻기 위해 가우시안 분포에서 샘플을 추출한다. 그러나 이 방법은 문제가 있는데, 왜냐면 우리가 VAE 모델을 훈련시키기 위해 경사하강법을 수행할 때, 샘플링 모듈을 통해 어떻게 역전파^{backpropagation}을 수행해야 하는지 모르기 때문이다.

대신에 우리는 $\boldsymbol{z}$ 를 “샘플링” 하기 위해 재매개변수화 트릭 을 사용한다. $\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$ 인 조건에서 $\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$ 를 이용한다. 이 경우, 훈련에서의 역전파가 가능하다. 구체적으로, 위 식에서 그래디언트는 (요소 별) 곱셈과 덧셈을 거쳐간다.

VAE 손실 함수 분리하기

잠재 변수 추정 및 재구성 손실 시각화

위에서 언급한 것과 같이 VAE의 손실 함수는 재구성 항과 정규화 항의 두 부분을 갖는다. 우리는 이를 다음과 같이 써 볼 수 있다.

손실 함수의 각 항이 지니는 목적을 시각화 하기 위해, 추정된 각각의 $\boldsymbol{z}$ 값을 $2d$ 공간의 원으로 생각해 볼 수 있는데, 여기서 $\mathbb{E}(\boldsymbol{z})$ 이 원의 중심이고 주변 영역은 $\mathbb{V}(\boldsymbol{z})$ 에 의해 결정되는 $\boldsymbol{z}$ 의 가능한 값이다.

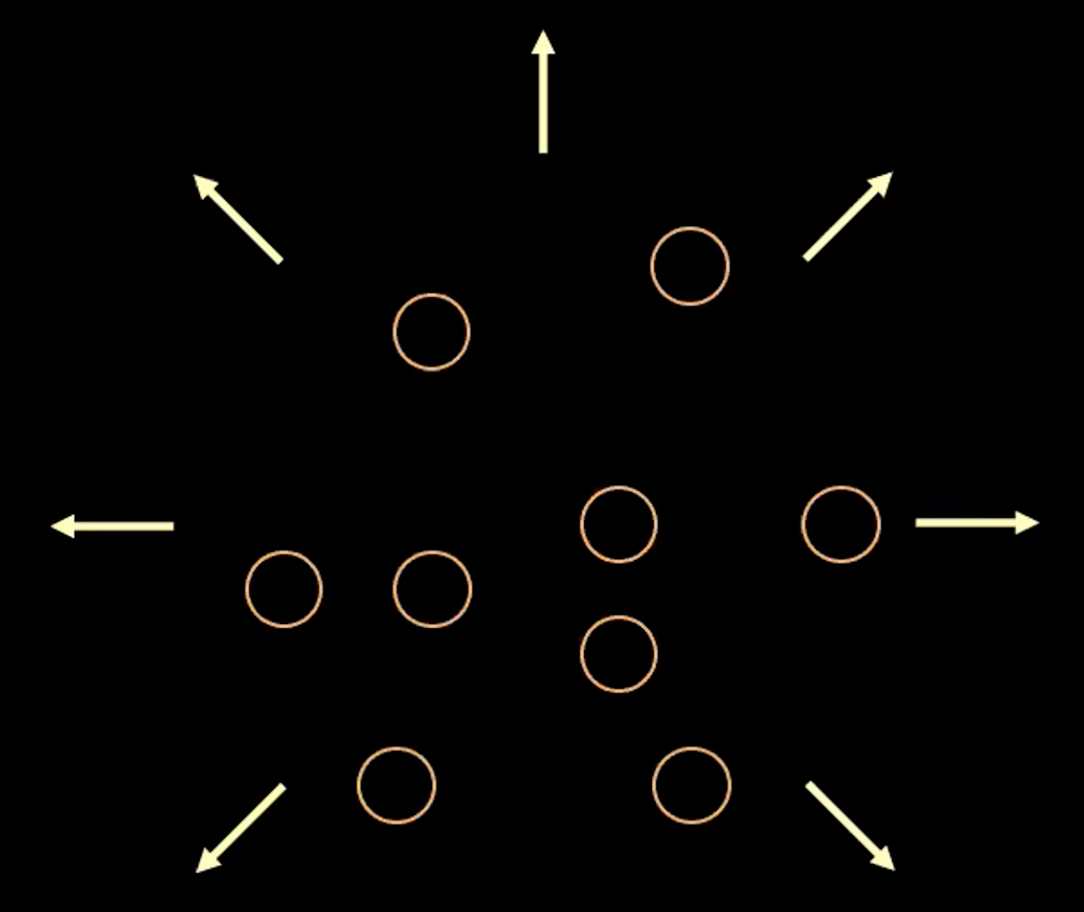
그림. 3: 잠재 공간에서의 벡터 $z$ 를 원으로 시각화

위의 그림 3에서, 각각의 원은 추정된 $\boldsymbol{z}$ 의 영역을 나타내며, 화살표는 어떻게 재구성 항이 각각의 추정된 값들을 다른 값으로 밀어내는지를 보여주며 이에 대한 자세한 설명은 아래에 있다.

만약 $z$ 의 추정된 값들 중 어느 두 개 사이에 겹치는 부분이 있다면, (시가적으로 두 원이 겹치는 경우) 이는 재구성 할 때의 모호성</sup>ambiguity</sup>을 만들어낸다. 왜냐하면 겹치는 부분 안에 있는 점들은 두 원본 입력 모두에 매핑될 수 있기 때문이다. 따라서 재구성 손실은 점들을 서로 밀어낸다.

그러나 우리가 재구성 손실을 사용하면, 추정된 값들은 서로 서로를 계속해서 밀어낼 것이고, 결국 전체 시스템은 폭발할 수 있다. 이 부분이 바로 벌칙 항이 소개되는 지점이다.

Note: 이진^binary 입력의 경우 재구성 손실은 다음과 같고

실제값^{real valued} 입력의 재구성 손실은 다음과 같다

벌칙^penalty 항

두 번째 항은 평균이 $\mathbb{E}(\boldsymbol{z})$ 이고 분산이 $\mathbb{V}(\boldsymbol{z})$ 인 가우시안 분포와 표준 정규 분포에서 나온 $\boldsymbol{z}$ 사이의 상대 코트로피^{relative entropy}(두 분포 사이의 거리 측정) 이다. VAE 손실 함수의 이 항을 전개하면 다음을 얻는다:

합계의 각 표현식에는 4 개이 항이 있다. 아래에서는 그림 4 의 처음 세 개 항을 작성하고 그래프를 그려본다.

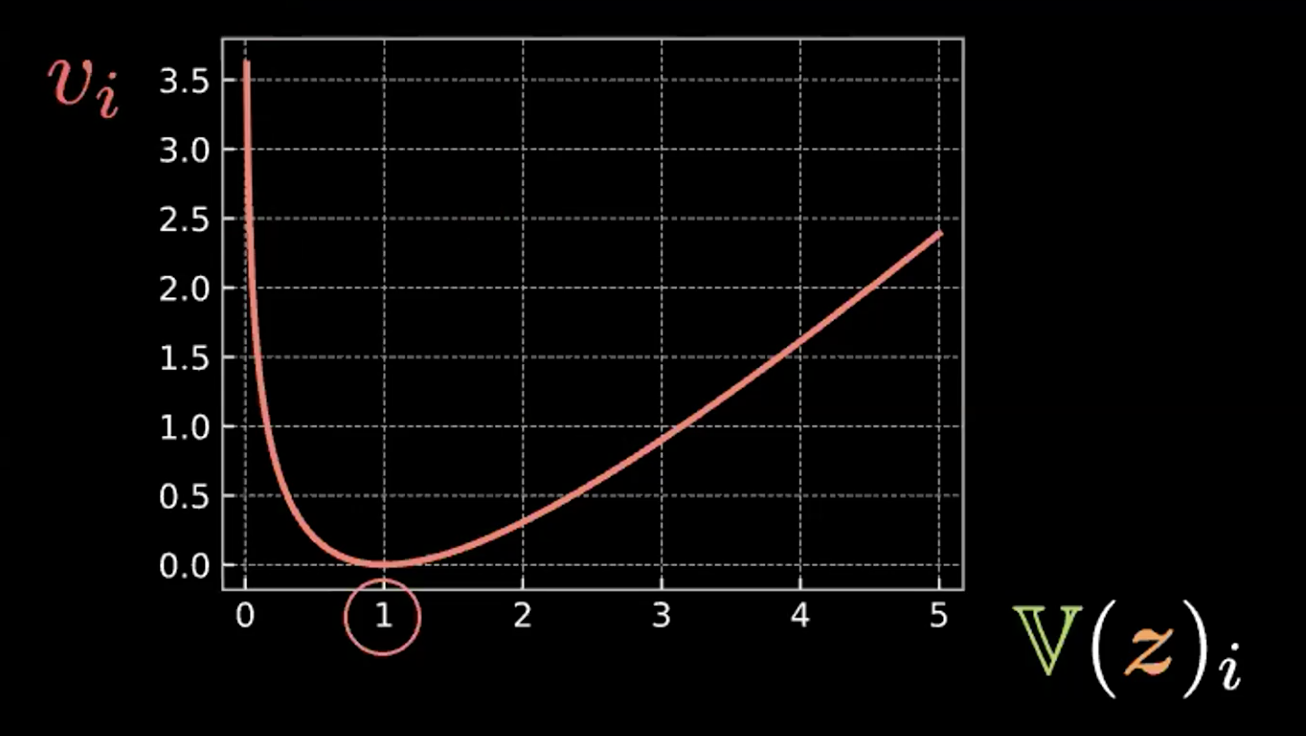
그림. 4: 상대 엔트로피가 원들의 분산이 1이 되도록 하는 방법을 보여주는 그림

따라서 $z_i$ 의 분산이 1일 때 이 표현식이 최소화되는 것을 확인할 수 있다. 그러므로 우리의 벌칙 손실은 추정한 잠재 변수들의 분산을 약 1로 유지시킨다. 시각적으로 표현하면, 위의 “원”들이 약 1의 반지름을 가질 것임을 뜻한다.

마지막 항 $\mathbb{E}(z_i)^2$ 은 $z_i$ 사이의 거리를 최소화하여서 재구성 항이 초래할 수 있는 “폭발” 을 방지한다.

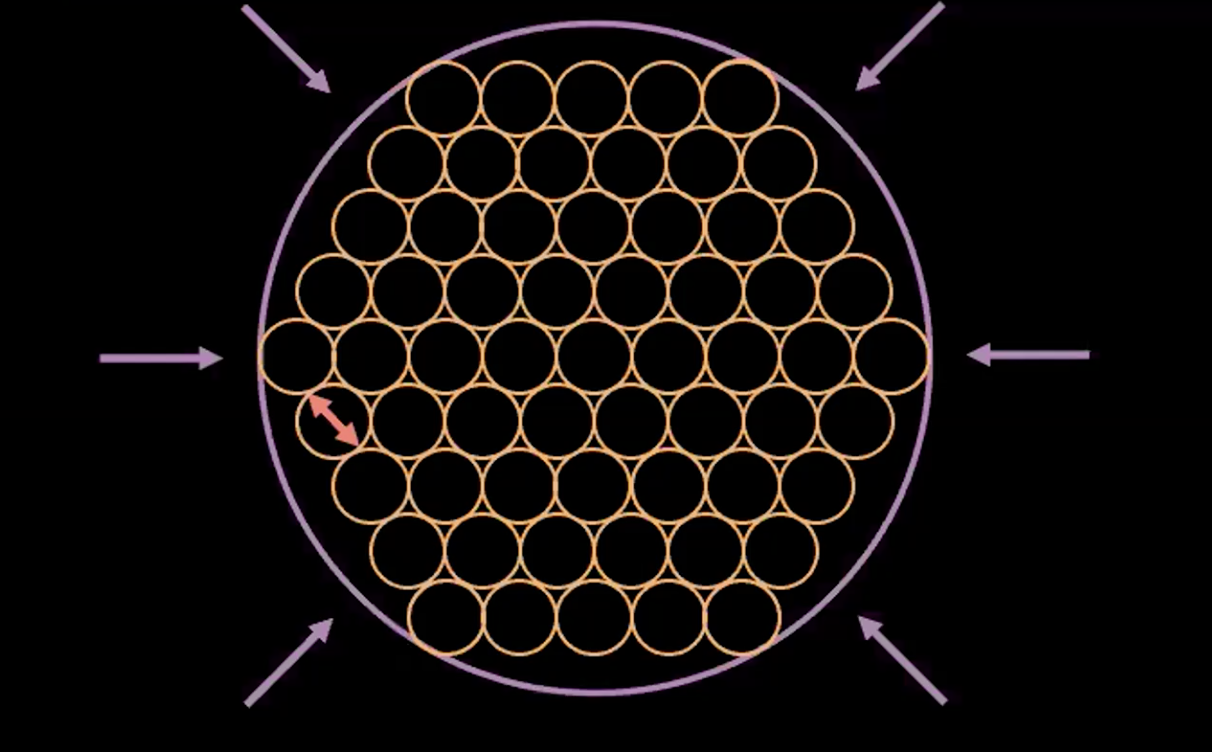
그림. 5: VAE의 "원 안의 원들^{bubble of bubble"} 해석

위의 그림 5는 VAE 손실이 각 점들의 추정된 분산을 약 1로 유지하면서 추정된 잠재 변수들이 서로 겹치지 않고 최대한 가깝게 우치하도록 어떻게 밀어붙이는지 보여준다.

참고: VAE 손실 함수의 $\beta$는 재구성과 벌칙 항에 가중치를 부여하는 방법을 지시하는 하이퍼파라미터^{hyperparameter}이다.

변이 오토인코더^{Variational Autoencoder} (VAE) 구현

주피터 노트북은 여기에서 확인할 수 있다.

이 노트북에서는 VAE를 구현하고 MNIST 데이터셋에 대해 훈련시킨다. 이 다음 정규 분포에서 $\boldsymbol{z}$ 를 샘플링하고 디코더에 투입하여 결과를 비교한다. 마지막으로 $\boldsymbol{z}$ 가 2D 투영^projection에서 어떻게 변하는지 살펴본다.

참고: 사용된 MNIST 데이터셋의 픽셀 값은 $[0, 1]$ 범위에 위치하도록 정규화 되었다.

인코더와 디코더

1. VAE 모듈에서 인코더와 디코더를 정의한다.
2. 인코더의 마지막 선형 레이어에서, $2d$ 사이즈로 출력값의 크기를 정하는데, 처음 $d$ 값은 평균이고 나머지 $d$ 값은 분산이다. 앞서 재매개변수화 트릭에서 설명한 것처럼 이러한 평균과 분산을 사용하여 $\boldsymbol{z} \in R^d$ 에서 샘플링을 진행한다.
3. 디코더의 마지막 레이어에서 우리는 시그모이드^sigmoid 활성화 함수를 이용해서 출력값의 범위가 입력값의 범위와 유사한 $[0, 1]$ 에 위치하도록 한다.

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

재매개변수화^{Reparameterisation}와 ‘포워드^forward’ 함수

재매개변수화 함수의 경우, 모델이 훈련 모드에 있을 때, 로그 분산 (logvar) 에서 표준 편차(std)를 계산한다. 분산이 음이 되지 않도록 하기 위해 분산 대신 로그 분산을 사용하고, 분산을 취하는 것은 분산의 전체 범위 확보를 보장하여 훈련 과정을 더욱 안정적으로 만든다.

훈련 과정 중에, 재매개변수화 함수는 훈련에서 역전파를 수행할 수 있도록 재매개변수화 트릭을 수행한다. 앞서 강의에서 설명했던 노란색 원들의 개념에 연결짓기 위해 함수가 호출될 때 마다 점 eps = std.data.new(std.size()).normal_() 을 그린다. 그래서 이를 100회 수행하면, 정규 분포이기 때문에 대략적으로 구^sphere의 모형을한 100개의 점을 얻는다. 그리고 선 eps.mul(std).add_(mu)은 이 구가 mu를 중심으로 반경이 std 가 되도록 한다.

포워드 함수의 경우 먼저 인코더에서 mu (전반) 그리고 logvar (후반)를 계산하고, 재매개변수화 함수를 통해 $\boldsymbol{z}$ 를 계산한다. 최종적으로 디코더의 출력을 반환한다.

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        eps = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

VAE에 대한 손실 함수

여기에서 우리는 재구성 손실 (이진 교차 엔트로피^{binary cross entropy})와 상대 엔트로피 (KL 발산^divergence 페널티)를 정의한다.

def loss_function(x_hat, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + KLD

새로운 샘플 생성

모델을 훈련시킨 뒤에, 정규 분포에서 임의의 $z$ 를 샘플링하여 디코더에 투입할 수 있다. 그림 6에서 디코더가 전체 잠재 공간을 모두 “덮지” 않았기 때문에 결과물이 좋지 않은 것을 볼 수 있다. 이는 모델을 더 많은 에폭^epochs의 학습을 통해 개선될 수 있다.

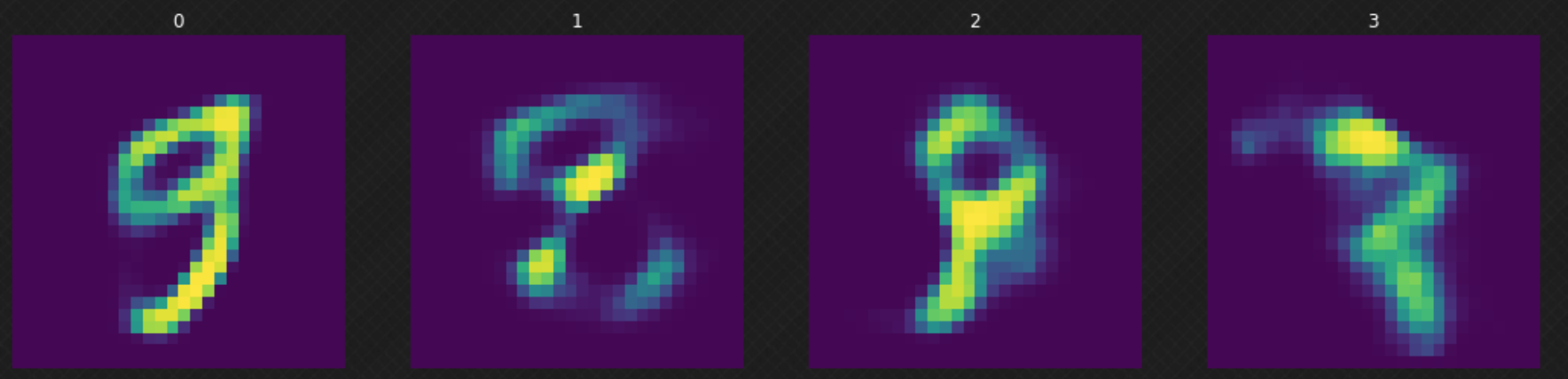
그림. 6: 잠재 공간 속 랜덤 이동

한 숫자가 다른 숫자로 어떻게 변화하는지 볼 수 있는데, 이는 오토인코더를 사용했더라면 불가능했을 부분이다. 잠재 공간으로 진입하면, 디코더의 출력은 여전히 제대로인것을 알 수 있다. 아래의 그림 7은 숫자 $3$이 어떻게 $8$로 변화하는지 보여준다.

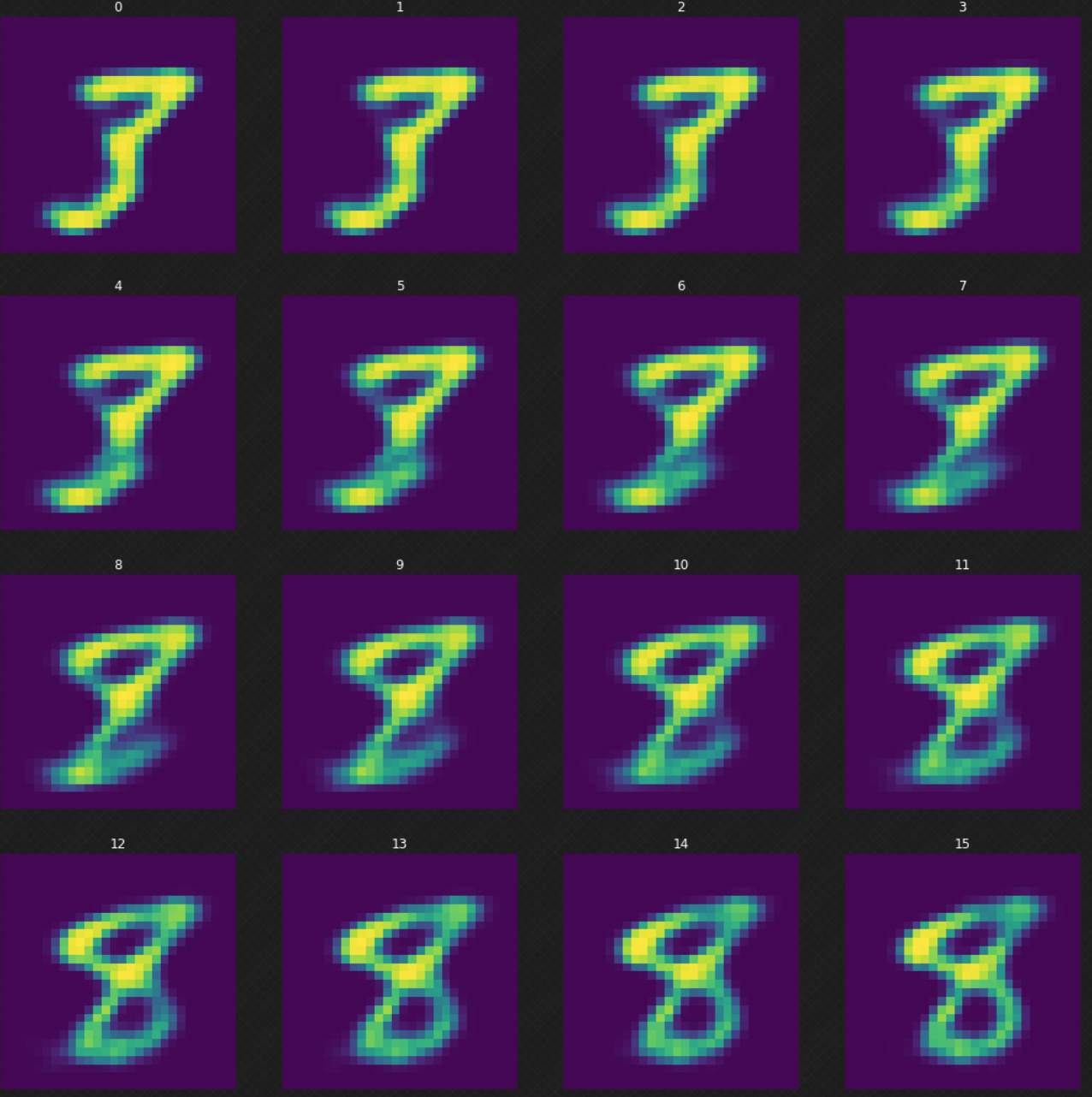
그림. 7: 숫자 3에서 8로의 변화

평균의 투영

마지막으로 훈련 중/후에 잠재 공간이 어떻게 변하는지 살펴보자. 그리 8에서 이어지는 차트는 2D 공간에 투영된, 각각의 색상상이 하나의 숫자를 의미하는, 인코더 출력의 평균이다. 에폭 0 에서는 클래스 중 매우 일부만 모여있고 전체적으로 여기저기 퍼져 있는 것을 볼 수 있다. 모델의 훈련이 진행되어감에 따라, 잠재 공간은 더욱 잘 정의되고 클래스 (숫자)들은 클러스터를 형성하기 시작한다.

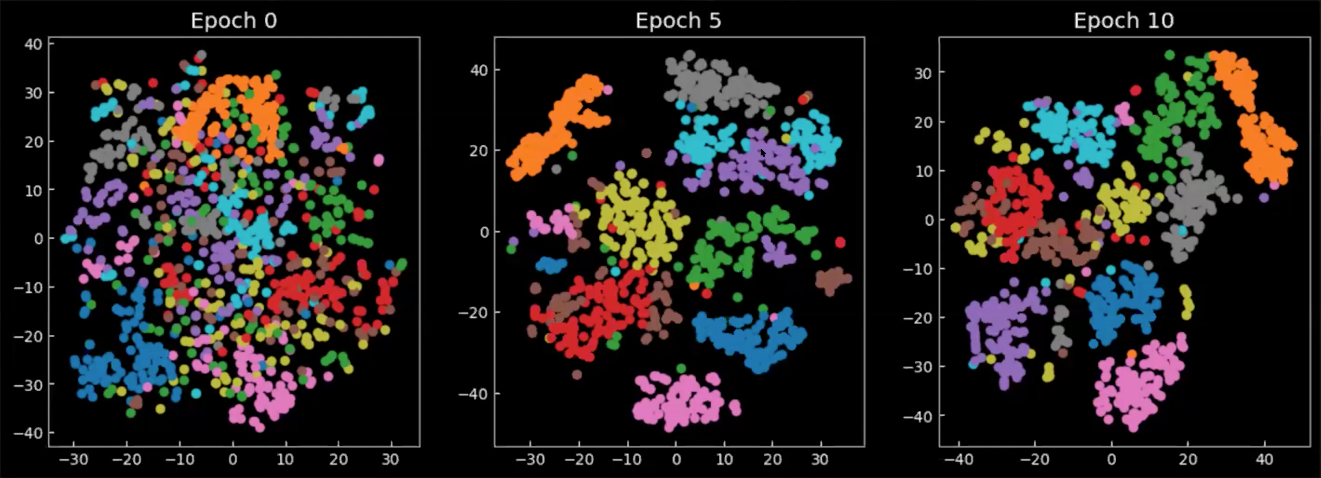
그림. 8: 잠재 공간에서 평균 $\E(\vect{z})$ 의 2D 투영