정규화 잠재 변수 에너지 기반 모델^{Regularized Latent Variable Energy Based Models}

정규화 잠재 변수 EBM

잠재 변수를 포함하는 모델은 관측된 입력 $x$ 와 추가적인 잠재 변수 $z$ 에 따라 예측 $\overline{y}$ 의 분포를 만들어 낼 수 있다. 에너지 기반 모델 또한 잠재 변수를 가질 수 포함할 수 있다.

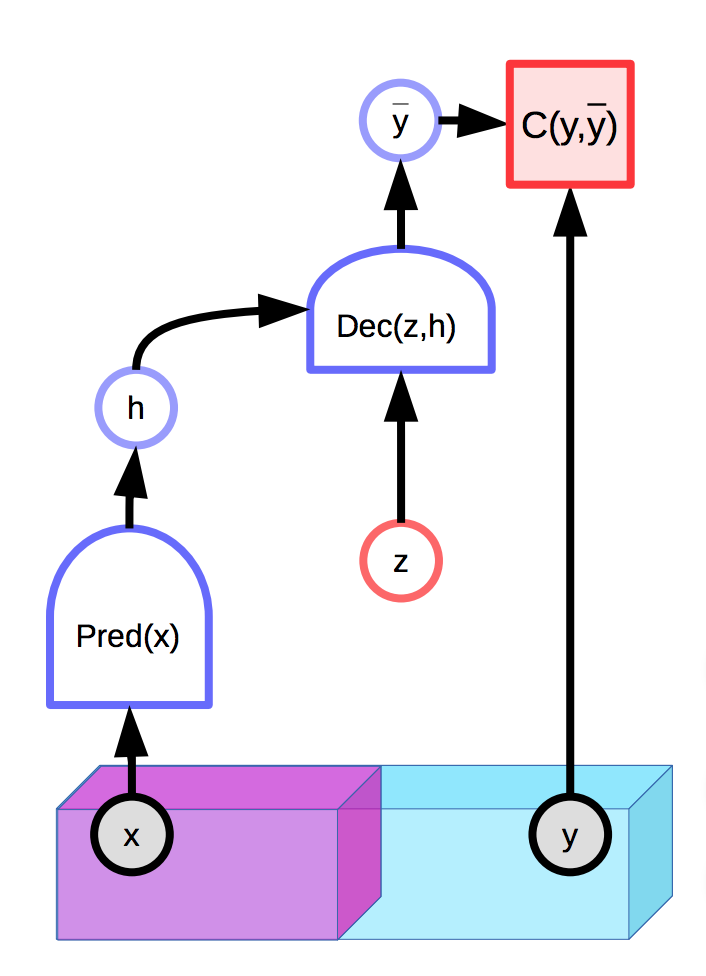
그림. 1: 잠재 변수를 가지는 EBM의 예시

이에 대한 자세한 내용은 이전 강의 노트에서 확인하기 바란다.

안타깝게도, 만일 잠재 변수 $z$ 가 최종 예측 $\overline{y}$ 를 만들어내는데 지나친 표현력^{expressive power}을 갖게 되면, 모든 실제 출력 $y$ 는 적절하게 선택된 $z$ 를 바탕으로 입력 $x$ 에서 완벽하게 재구성된다. 이는 $y$ 와 $z$ 모두에 대해 추론^inference 과정 동안 에너지가 최적화되어, 모든 지점의 에너지 함수 값이 0이 됨을 의미한다.

이에 대한 자연스러운 해결책은 잠재 변수 $z$ 의 정보 용량을 제한하는 것이다. 이를 수행하는 한 방법은 잠재 변수를 정규화 하는 것이다:

이 방법은 값이 작은 $z$ 의 공간과 이에 대해 낮은 에너지를 갖는 $y$ 의 공간을 제어하는 값을 제한한다. $\lambda$ 의 값은 이러한 트레이드오프^trade-off를 조절한다. $R$ 의 유용한 예시는 $L_1$ 놈^norm인데, 이는 거의 모든곳에서 미분이 가능한 유효 차원의 근사치로 볼 수 있다. $L_2$ 놈을 제한하면서 $z$ 에 노이즈를 추가하여 정보 내용 (VAE)도 제한할 수 있다.

스파스 코딩(희소 코딩)

스파스 코딩은 기본적으로 구간별^piecewise 선형 함수를 이용해 데이터를 근사하고자 하는 무조건 정규화를 이용한 잠재 변수 EBM의 예시이다.

$n$-차원 벡터 $z$ 는 $m « n$ 인 0이 아닌 구성요소를 최대한으로 보유하려는 경향이 있다. 그러면 각각의 $Wz$ 는 $W$ 의 $m$ 개 칼럼의 스팬(생성)^span에 속하게 된다.

각각의 최적화 단계 후에는 행렬 $W$ 와 잠재 변수 $z$ 는 $W$의 열의 $L_2$ 놈의 합으로 정규화된다. 이를 통해 $W$ 와 $z$ 가 무한대와 0 으로 발산하지 않도록 한다.

FISTA

그림. 2: FISTA 연산 그래프

FISTA (fast ISTA, 빠른 ISTA)는 $\Vert y - Wz\Vert^2$ 와 $\lambda \Vert z\Vert_{L^1}$ 두 항을 번갈아 가면서 최적화 하며 $z$ 에 대한 스파스 코딩 에너지 함수 $E(y,z)$ 를 최적화하는 알고리즘이다. $Z(0)$ 를 초기화하고 다음의 규칙에 따라 반복적으로 $Z$ 를 업데이트 한다:

내부 표현식 $Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$ 은 $\Vert y - Wz\Vert^2$ 항의 그래디언트^gradient 단계이다. 이 다음, $\text{Shrinkage}$ 함수는 값을 0 쪽으로 이동하여 $\lambda \Vert z\Vert_{L_1}$ 항을 최적화한다.

LISTA

FISTA 는 고차원의 대규모 데이터셋 (예. 이미지)에 적용하기에는 굉장히 비용 소모가 크다. 이를 보다 효율적으로 만드는 한 가지 방법은 최적의 잠재 변수 $z$ 를 예측하도록 네트워크를 훈련시키는 것이다:

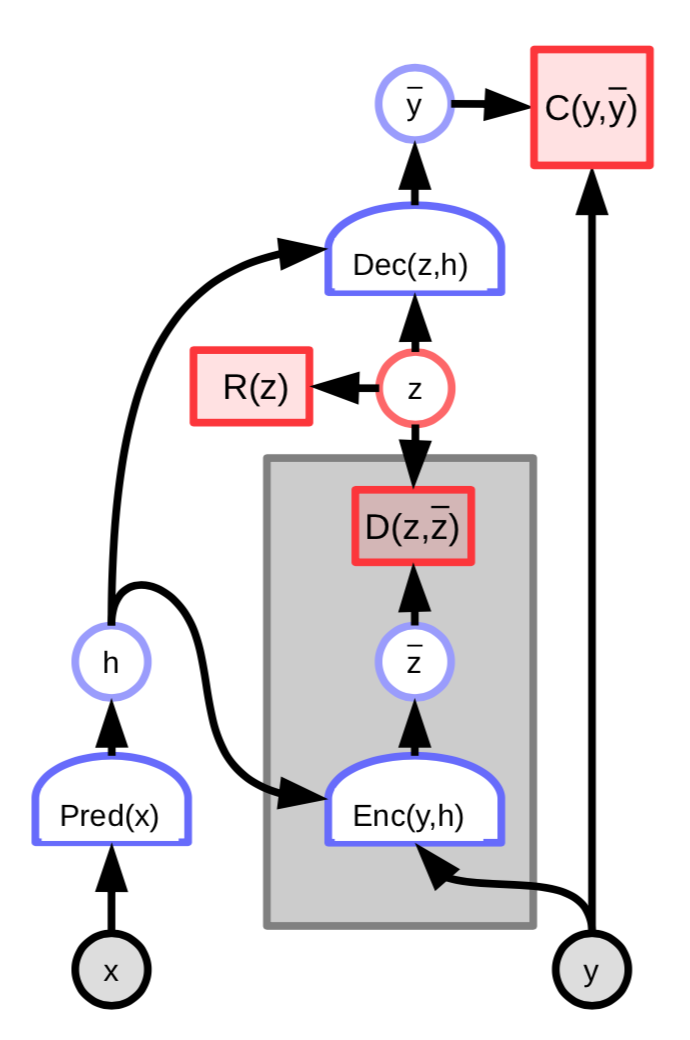
그림. 3: 잠재 가변 인코더를 가지는 EBM

그러면 이 에너지의 아키텍쳐에는 예측된 잠재 변수 $\overline z$ 와 최적의 잠재 변수 $z$ 의 차이를 측정하는 추가 항이 더해진다:

추가적으로 다음을 정의하고

다음과 같이 작성한다

이 업데이트 규칙은 반복적으로 잠재 변수 $z$ 를 결정하는 매개변수 $W_e$ 를 학습하는 순환 신경망으로 이해할 수도 있다. 이 신경망은 정해진 $K$ 시간 단계 동안 실행되고 $W_e$ 의 그래디언트는 표준 BPTT^{standard backpropagation-through-time}를 사용해서 계산된다. 훈련이 완료된 네트워크는 FISTA 알고리즘보다 적은 반복으로도 좋은 $z$ 를 만들어낸다.

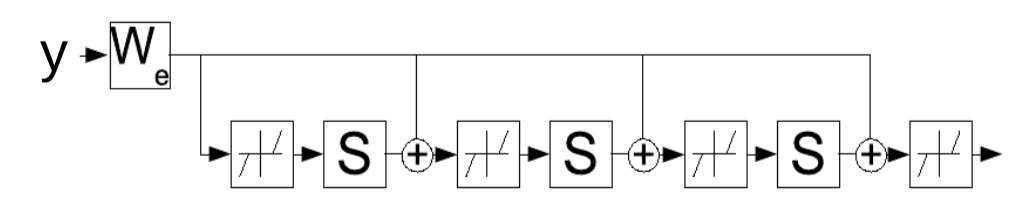
그림. 4: 시간의 흐름에 따라 펼쳐져 제시된 순환 신경망으로써의 LISTA.

스파스 코딩 예시

256 차원의 잠재 벡터를 갖는 스파스 코딩 시스템이 MNIST 손글씨 숫자 데이터에 적용되면, 이 시스템은 전체 트레이닝 데이터 셋을 유사하게 재현해 낼 수 있는 선형으로 결합할 수 있는 256 스트로크 세트를 학습한다. 스파스 정규화^{sparse regularizer}는 이 데이터가 작은 수의 스트로크만으로도 재현될 수 있도록한다.

그림. 5: MNIST에 대한 스파스 코딩. 각 이미지는 $W$ 의 칼럼을 학습함.

스파스 코딩 시스템이 자연 이미지 조각에 대해 훈련되면, 학습되는 특징은 방향 있는 가장자리(모서리)에 반응하는 가버(Garbor) 필터이다. 이러한 특징은 초기의 동물 시각 시스템에서 학습되는 특징과 유사하다.

합성곱 스파스 코딩

이미지와 이미지의 특징 맵 ($z_1, z_2, \cdots, z_n$)이 주어졌다고 가정하자. 그러면 각각의 특징 맵을 커널 $K_i$ 와 곱 ($*$) 할 수 있다. 이를 통해 재구성된 것을 다음과 같이 간단하게 계산할 수 있다:

이는 재구성이 $Y=\sum_{i}W_iZ_i$ 로 수행된 원래의 스파스 코딩과 다르다. 보통의 스파스 코딩에서는, 가중치가 $Z_i$ 의 계수로 주어지는 칼럼의 가중합을 가진다. 합성공 스파스 코딩에서는, 여전히 선형 연산이지만 이제 사전 행렬^{dictionary matrix}은 특징 맵의 모음이고 각각의 특징 맵을 각각의 커널과 곱해서 결과값을 합한다.

자연 이미지에 대한 합성곱 스파스 오토인코더

그림.6 획득한 필터 및 기저 함수^{basis functions}. 선형 합성곱 디코더^decoder

인코더와 디코더의 필터는 매우 비슷하게 생겼다. 인코더는 간단히 말해서 합성곱 후에 비선형 함수를 거치고 이어서 스케일을 변경하기 위한 대각^diagonal 레이어를 갖는다. 그 다음 코드 제약 조건에 희소성^sparsity을 갖는다. 디코더는 단순히 합성곱 선형 디코더이고 여기에서의 재구성은 제곱 오류^{square error}이다.

따라서, 필터를 만약에 단 하나만 적용한다면 이것은 중앙 서라운드 타입^{centre surround type} 필터이다. 두 개의 필터를 이용하면 이상한 모양의 필터를 얻게 된다. 네 개의 필터가 있다면, 방향이 있는 가장자리^{oriented edges} (가로 및 세로), 즉 각 필터마다 2개의 극성^polarity을 얻는다. 여덟개의 필터가 있으면 서로 다른 8개 방향에서 방향이 있는 가장자리를 얻을 수 있다. 16개의 필터로는 중앙부를 중심으로 더 많은 방향에서 그와 같은 가장자리를 얻는다. 필터의 갯수를 늘려감에 따라, 가장자리를 감지해 내는 것 이외에도 더 많은 수의 다양한 필터를 얻고, 뿐만 아니라 다양한 방향과 중심부 등을 감지해 내는 것들도 얻는다.

이러한 현상은 우리 뇌의 시각 피질에서 관찰된 것과 유사하기 때문에 흥미로워 보인다. 따라서 이는 곧 우리가 완전히 비지도적인 방식으로 굉장히 좋은 특징들을 학습해 낼 수 있다는 것을 의미한다.

부수적으로, 이러한 특징들을 가져와서 합성곱 신경망에 장착하고 어떤 작업에 대해 훈련시키면, 이미지에 대해 처음부터 훈련시키는 것보다 더 나은 결과물을 얻는 것은 아니다. 그렇지만, 이 과정 중에는 성능을 크게 향상 시킬 수 있는 부분이 있다. 예를 들어서, 샘플의 수가 충분히 많지 않거나 카테고리가 거의 없는 경우에는 순수하게 지도적인^supervised 방식을 통해 훈련시키면 우리는 품질이 낮은 특징만을 얻는다.

그림. 7 컬러 이미지에 대한 합성곱 스파스 인코딩

위의 그림은 컬러 이미지의 또 다른 예시이다. 디코딩 커널 (오른쪽)의 크기는 9x9 이다. 이 커널은 전체 이미지에 대해 합성곱 방식으로 적용된다. 왼쪽의 이미지는 인코더의 스파스 코드이다. $Z$ 벡터는 흰색 또는 검은색(회색이 아닌 것) 구성 요소가 거의 없는 매우 희소한 공간이다.

변이형 오코인코더^{Variational autoencoder}

변이형 오토인코더는 정규화된 잠재 변수 EBM에서 희소성 부분만을 제외한 것과 유사한 구조를 가지고 있다. 대신에, 코드의 정보 내용은 노이즈 때문에 제한된다.

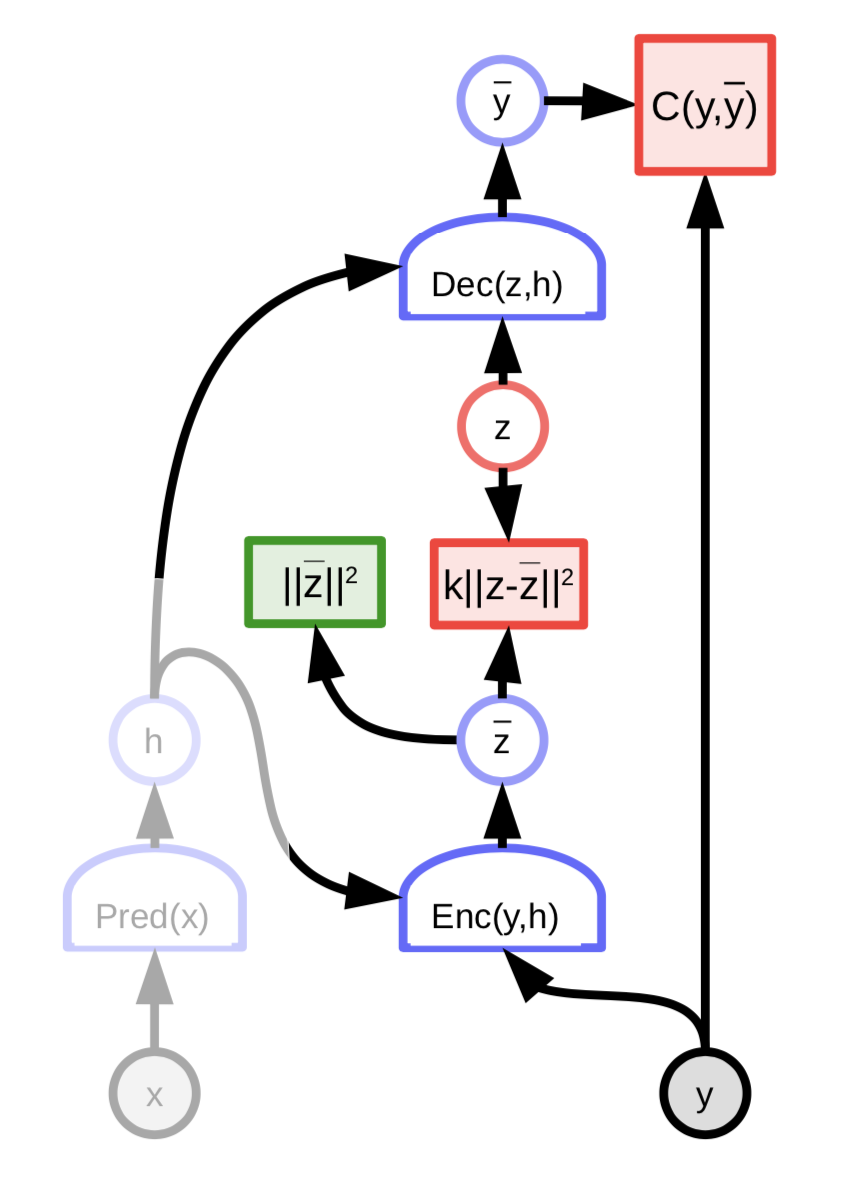
그림. 8: 변이형 오토인코더의 구조

잠재 변수 $z$ 는 $z$ 에 대한 에너지 함수를 최소화하여 계산되는게 아니다. 대신에, 에너지 함수는 로그 값이 ${\overline z}$ 에 연결되는 비용의 분포에 따라 랜덤하게 $z$ 를 샘플링하는 것으로 간주된다. 이 분포는 평균이 ${\overline z}$ 인 가우시안 분포이고 이에 따라 ${\overline z}$ 에 가우시안 노이즈가 추가된다.

가우시안 노이즈가 추가된 코드 벡터는 그림 9(a)에서 보이는 것과 같이 퍼지 볼^{fuzzy ball}로 시각화 될 수 있다.

|

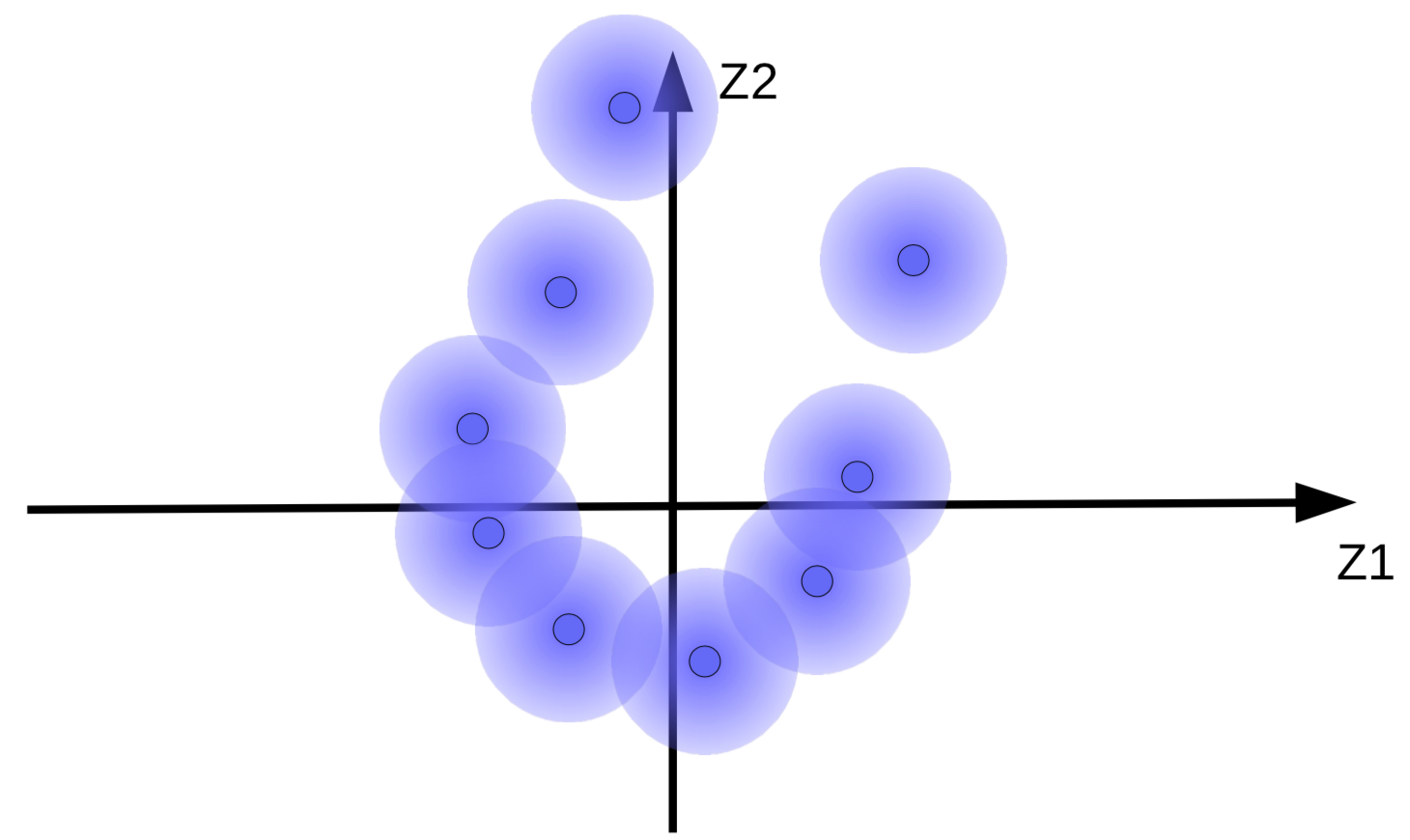
(a) 원래의 퍼지 볼 세트

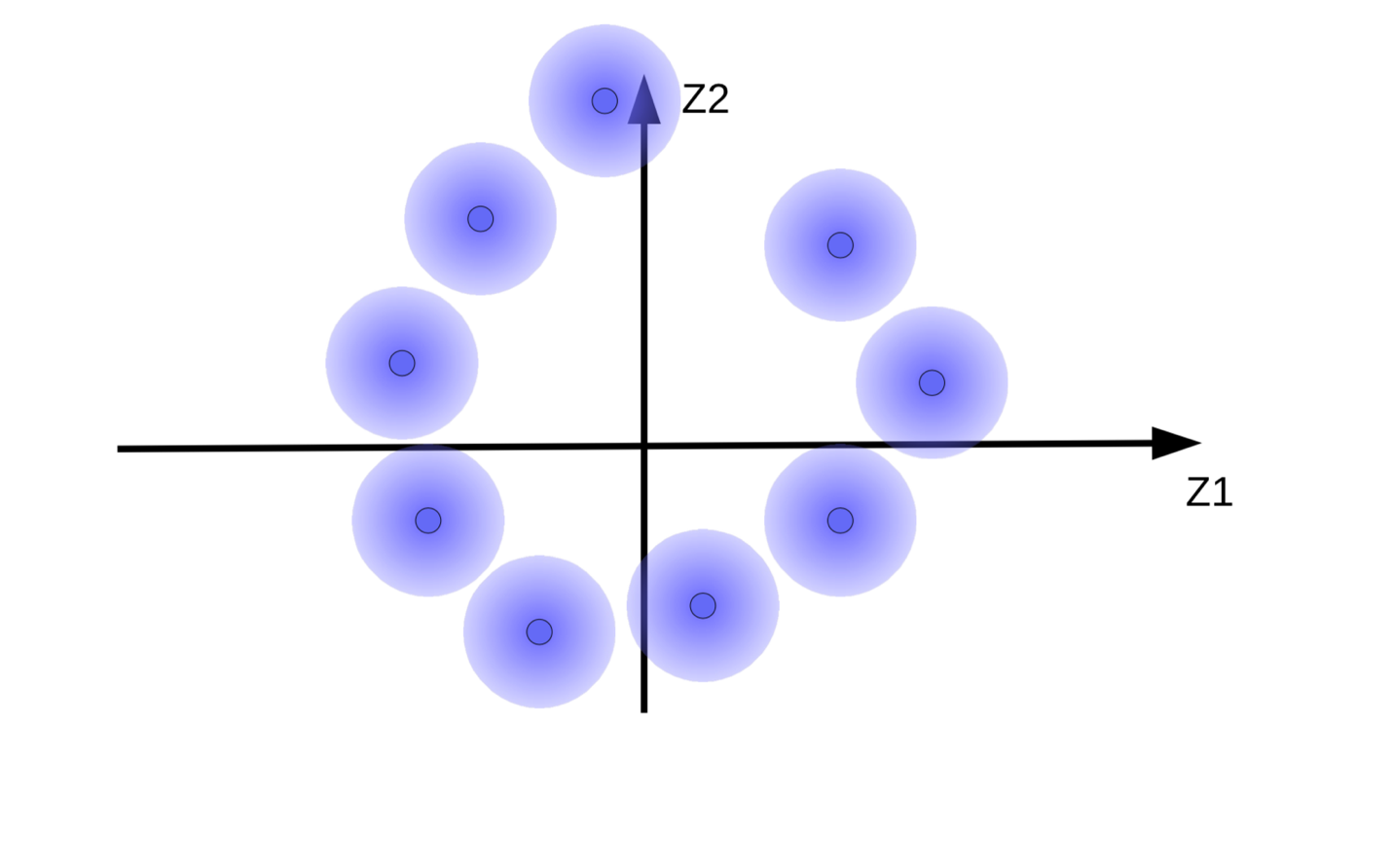
(b) 정규화 없는 에너지 최소화 과정에 따른 퍼지볼의 움직임

이 시스템은 코드 벡터 ${\overline z}$ 를 가능한한 크게 만들어서 $z$(노이즈)의 영향을 최소화 하고자 한다. 이는 그림 9(b) 에서 보이는 것과 같이 퍼지 볼들이 원점에서 멀리 떨어져 떠다니게 한다. 코드 벡터를 크게 만드려고 하는 또 다른 이유는 재구성 중에 디코더가 서로 다른 샘플을 혼동하게 하는 퍼지 볼 사이의 겹침^overlapping을 방지하기 위해서이다.

하지만 만일 매니폴드가 있다면, 우리는 퍼지 볼들이 그 주변에서 클러스터링 되기를 원한다. 따라서 코드 벡터는 평균과 분산이 0에 까까워지도록 정규화된다. 이를 위해 그림 10과 같이 코드 벡터들을 원점과 스프링으로 연결한다.

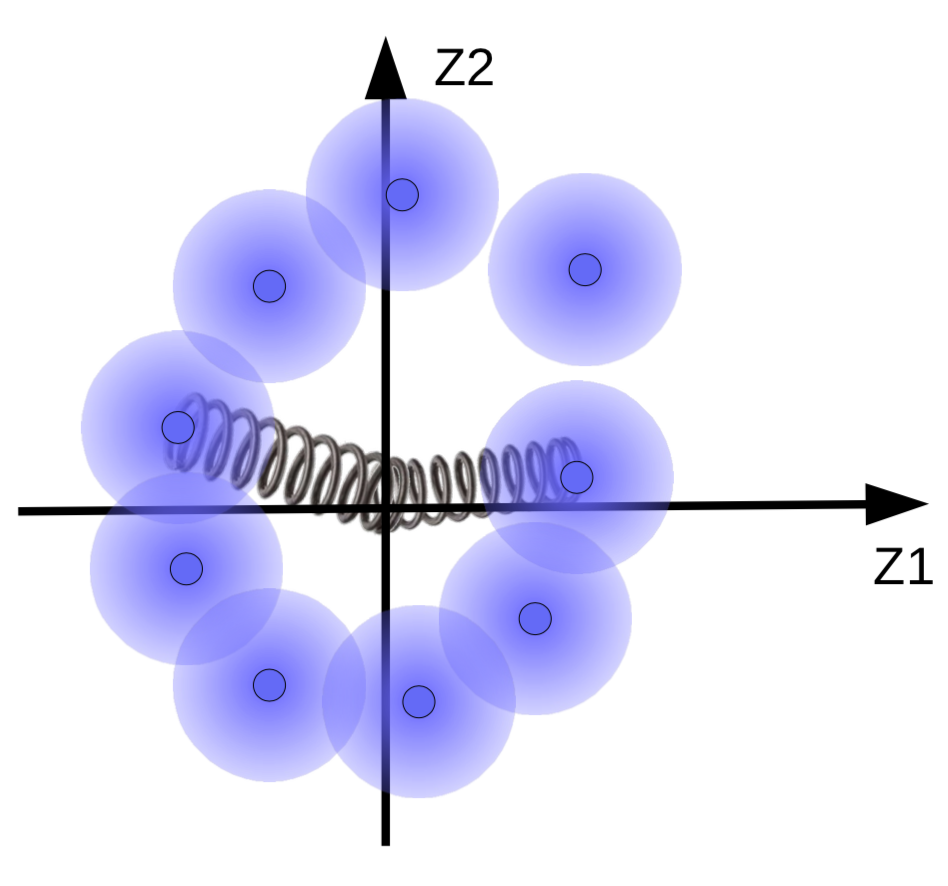
그림. 10: 스프링과 함께 시각화된 정규화의 효과

스프링의 강도는 퍼지 볼이 원점과 얼마나 가까이 위치할지를 결정한다. 만일 스프링이 너무 약하다면 퍼지 볼이 원점으로부터 굉장히 멀리에 위치한다(날아가 버린다). 그리고 이게 너무 강하면, 퍼지 볼들은 원점에 지나치게 가까이 붙어버려서 높은 에너지 값을 낳는다. 이를 방지하기 위해서, 시스템은 해당 샘플이 유사한 경우에만 이 구(퍼지 볼)^sphere들이 서로 겹치는 것을 허용한다.

퍼지 볼의 크기를 조정하는 것 또한 가능하다. 이 부분은 퍼지 볼의 사이즈가 너무 크거나 작아서 서로 붙어버리지 않도록 분산을 1에 가깝게 만드는 페널티 함수 (KL 발산(KL Divergence))에 의해 제한된다.