오토인코더^Autoencoders 입문

오토인코더 응용

이미지 생성

그림. 1 에서 어떤 얼굴이 가짜인지 알 수 있을까? 사실 두 사진 모두 StyleGan2 생성기로부터 만들어진 이미지이다. 얼굴 자체의 세세한 부분은 매우 사실적이지만, 배경은 이상하게 보인다 (왼쪽: 흐릿함, 오른쪽: 기형의 물체). 이는 신경망이 얼굴 샘플에 대해서 훈련되기 때문이다. 배경은 훨씬 더 높은 변동성^variability를 갖는다. 여기서 데이터 매니폴드^manifold는 얼굴 이미지의 자유도^{degrees of freedom}와 동일한 대략 50 차원을 갖는다.

그림. 1: StyleGan2을 통해 생성된 얼굴들

픽셀 공간^{Pixel Space}와 잠재 공간^{Latent Space} 사이의 보간^{Interpolation} 차이

그림. 2: 개와 새

픽셀 공간에서 개와 새의 이미지 (그림. 2)를 선형으로 보간하면^{linearly interpolate}, 그림. 3에서 볼 수 있듯 두 이미지의 페이딩 오버레이^{fading overlay}가 나타난다. 왼쪽 상단에서 오른쪽 하단으로 갈수록, 개 이미지의 가중치가 감소하고 새 이미지의 가중치는 증가한다.

그림. 3: 보간의 결과

만일 두 개의 잠재 공간 표현^{latent space representation}을 보간하고 디코더^decoder에 투입하면, 그림. 4에서 확인할 수 있듯, 개에서 새로의 변환^{transformation}을 얻는다.

그림. 4: 디코더에 투입한 결과

당연하게도, 잠재 공간이 이미지 구조를 파악하는데 더욱 좋다.

변환 예시^{Transformation Examples}

그림. 5: 확대^Zoom

그림. 6: 이동^Shift

그림. 7: 밝기^Brightness

그림. 8: 회전^Rotation (회전은 3D 일 수 있음)

이미지 초 고해상도^{Super-resolution}

이 모델은 이미지의 해상도를 높이고^{upscale images}, 원래 얼굴을 재건하는 것을 목표로 한다. 그림.9 에서 왼쪽에서 오른쪽으로 첫 번째 열은 16x16 입력 이미지이고, 두 번째는 표준 bicubic 보간^{Standard bicubic interpolation}을 통해 얻을 수 있는 이미지이고, 세 번째는 신경망에 의해 생성된 출력이며, 마지막 오른쪽은 실제^{ground truth} 이미지이다. (https://github.com/david-gpu/srez)

그림. 9: 원래 얼굴 재건하기^{reconstructing original faces}

출력 이미지에서 학습 데이터에 편향^bias이 있어서 재건된 얼굴이 부정확함을 분명하게 알 수 있다. 예를 들어서, 왼쪽 상단 아시안 남자는 불균형한 훈련 이미지 데이터로 인해 유럽인처럼 보이는 이미지로 출력되었다. 왼쪽 하단에서 여성의 재건된 얼굴 이미지의 경우, 훈련 데이터에서 다양한 각도에서 촬영된 이미지가 부족하여 이상하게 보인다.

이미지 복원^inpainting

그림. 10: 얼굴에 회식 패치^patch 넣기

그림. 10과 같이 얼굴에 회색 패치를 넣으면 이미지가 훈련 매니폴드에서 멀어진다. 그림. 11의 얼굴 재건은 에너지 함수 최소화^{Energy function minimization}를 통해 훈련 매니폴드에서 가장 가까운 샘플 이미지를 찾아 수행된다.

그림. 11: 그림. 10에서 재건된 이미지

이미지 설명(캡션)^caption

그림. 12: 이미지 예시에 대한 설명

그림 12의 텍스트 설명에서 이미지로의 번역은 중요한 시각적 정보와 관련된 텍스트의 특징 표현을 추출하고, 이를 이미지로 디코딩하여 이루어진다.

오토인코더는 무엇인가?

오토인코더는 비지도^unsupervised 방식으로 훈련된 인공 신경망으로, 먼저 데이터에 인코딩 된 표현을 학습한 다음, 학습 된 인코딩 표현에서 입력 데이터를 (가능한한 가깝게) 생성하는 것을 목표로 한다. 따라서, 오토인코더의 출력은 입력에 대한 예측이다.

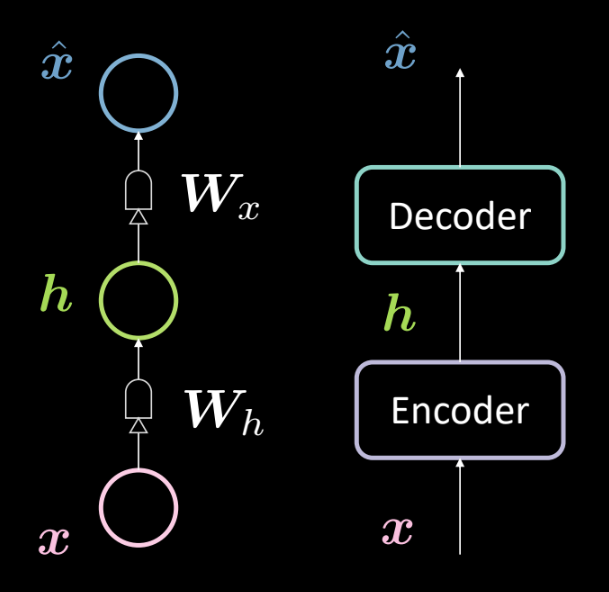
그림. 13: 기본 오토인코더의 아키텍쳐^architecture

그림 13은 기본 오토인코더의 아키텍쳐를 보여준다. 이전과 마찬가지로, 인코더 ($\boldsymbol{W_h}$로 정의되는 아핀 변환^{affine transformation} 후 스쿼싱^squashing)를 거치는 입력 $\boldsymbol{x}$으로 맨 아래서부터 시작한다. 이는 중간 은닉층^{hiddenn layer} $\boldsymbol{h}$을 형성한다. 이는 디코더 (또 다른 $\boldsymbol{W_x}$ 로 정의되는 아핀 변환 다음에 또 다른 스쿼싱이 뒤따름)의 대상이 된다. 그러면 모델의 입력에 대한 예측/재건인 출력 $\boldsymbol{\hat{x}}$ 이 생성된다. 우리는 이를 관습^convention에 따라 3층 신경망으로 부른다.

다음 방정식을 사용해서 위의 네트워크를 수학적으로 표현할 수 있다:

또한 다음의 차원을 지정할 수 있다:

참고: PCA를 나타내기 위해서, $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$ 로 정의된 타이트 가중치^{tight weights} (또는 묶인^tied 가중치)를 가질 수 있다.

왜 오토인코더를 사용할까?

이 시점에서, 입력을 왜 예측할 필요가 있는지, 그리고 오토인코더를 어떻게 응용할 수 있는지 의문을 가질 수 있다.

오토인코더의 주요^primary 응용 분야는 이상 감지^{anomaly detection} 또는 이미지 노이즈 제거^{image denoising}이다. 오토인코더의 작업이 매니폴드 즉 주어진 데이터 매니폴드에 있는 데이터를 재건하는 것임을 알고 있고, 오토인코더가 해당 매니폴드 안에 존재하는 입력만 재건할 수 있기를 원한다. 따라서 우리는 모델이 훈련 중에 관찰한 것들만을 재건할 수 있도록 제한하고, 따라서 새로운 입력에 존재하는 어떠한 변화^variation도 제거되는데, 왜냐하면 이 모델은 이러한 미세한 변화^{perturbations}에 영향을 받지 않을^insensitive 것이기 때문이다.

오토인코더의 또 다른 응용은 이미지 압축기^compressor이다. 만일 입력 차원 $n$ 보다 낮은 중간 차원 $d$ 를 갖고 있다면, 인코더는 압축기로 사용될 수 있고, 은닉 표현^{hidden representation} (코딩 된 표현)은 특정 입력의 모든 (또는 대부분) 정보를 전달하지만 적은 공간을 차지한다.

재건^{Reconstruction} 손실

이제 일반적으로 사용하는 재건 손실에 대해 살펴보자. 데이터셋의 전체적인 손실은 샘플 손실 당 평균으로 주어진다. 즉,

입력이 범주형^categorical이면, 교차 엔트로피 손실^{Cross-Entropy loss}를 사용해서 다음과 같은 샘플당 손실을 계산할 수 있다.

그리고 입력이 실수값^real-valued, 다음과 같이 주어지는 평균 제곱 오차^{Mean Squared Error} 손실을 사용할 수 있다.

완전하지 않은^Under-/과잉-완전^{over-complete} 은닉층^{hidden layer}

은닉층의 $d$ 차원이 입력의 $n$ 차원 보다 작으면 완전^complete 은닉층 아래에 있다고 말한다. 마찬가지로, $d>n$ 일 때, 과잉-완전^{over-complete} 은닉층이라고 부른다. 그림. 14는 왼쪽에서 완전하지 않은^{under-complete} 은닉층을 보여주고 과잉-완전 은닉층을 오른쪽에서 보여주고 있다.

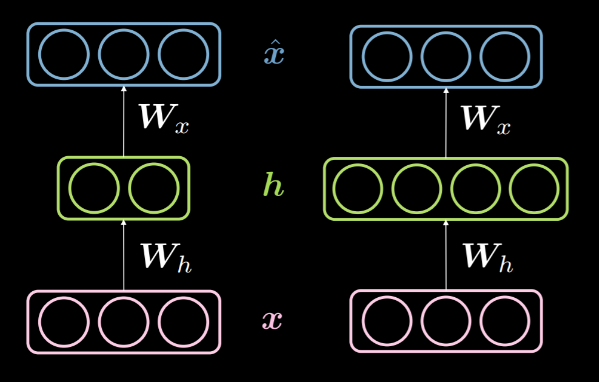
그림. 14: 완전하지 않은 *vs.* 과잉-완전 은닉층

위에서 논의한 바와 같이, 완전하지 않은 은닉층은 입력 정보를 더 낮은 차원으로 인코딩하기 때문에 정보를 압축^compression하는 데에 사용할 수 있다. 반면에, 과잉-완전 층에서는 입력보다 차원이 높은 인코딩을 사용한다. 이는 최적화를 더 용이하게 한다.

입력을 재건하고자 하기 때문에, 이 모델은 모든 입력 특성을 은닉층에 복사하고 출력으로 전달해서 본직적으로 항등 함수^{identity function} 으로 기능하는 경향이 있다. 이는 이 모델이 아무것도 학습하지 못했다는 것을 의미하기 때문에 이런 결과는 피해야한다. 따라서, 정보 병목 현상^bottleneck을 적용해서 추가적인 제약을 해야 한다. 은닉층이 훈련 중에 관찰된 구성으로만 가능 구성을 제한해서 이를 수행한다. 이는 (입력 공간의 하위 집합으로 제한된) 선택적 재건^{selective reconstruction} 을 허용하고 매니폴드에 없는 모든 것에는 둔감하게 만든다.

완전하지 않은^{under-complete} 층은 은닉층이 입력을 복사하기에 충분하지 않은 차원을 가지기 때문에 항등함수로 동작할 수 없다는 것을 유의해야 한다. 따라서 완전하지 않은 은닉층은 과잉-완전 은닉층에 비해서 과적합^overfit할 가능성이 적지만, 여전히 과적합할 수는 있다. 예를 들어서, 강력한 인코더와 디코더가 주어졌을 때, 모델은 단순하게 하나의 숫자를 각각의 데이터 포인트에 연결하고 이 매핑^mapping을 학습할 수 있다. 정규화 방법^{regularization methods}, 아키텍처 방법^{architectural methods} 등과 같은 과적합을 방지하는 몇 가지 방법이 있다.

노이즈 제거^Denoising 오토인코더

그림.15는 노이즈 제거 오토인코더의 매니폴드와 이것이 어떻게 작동하는지 직관적으로 여준다.

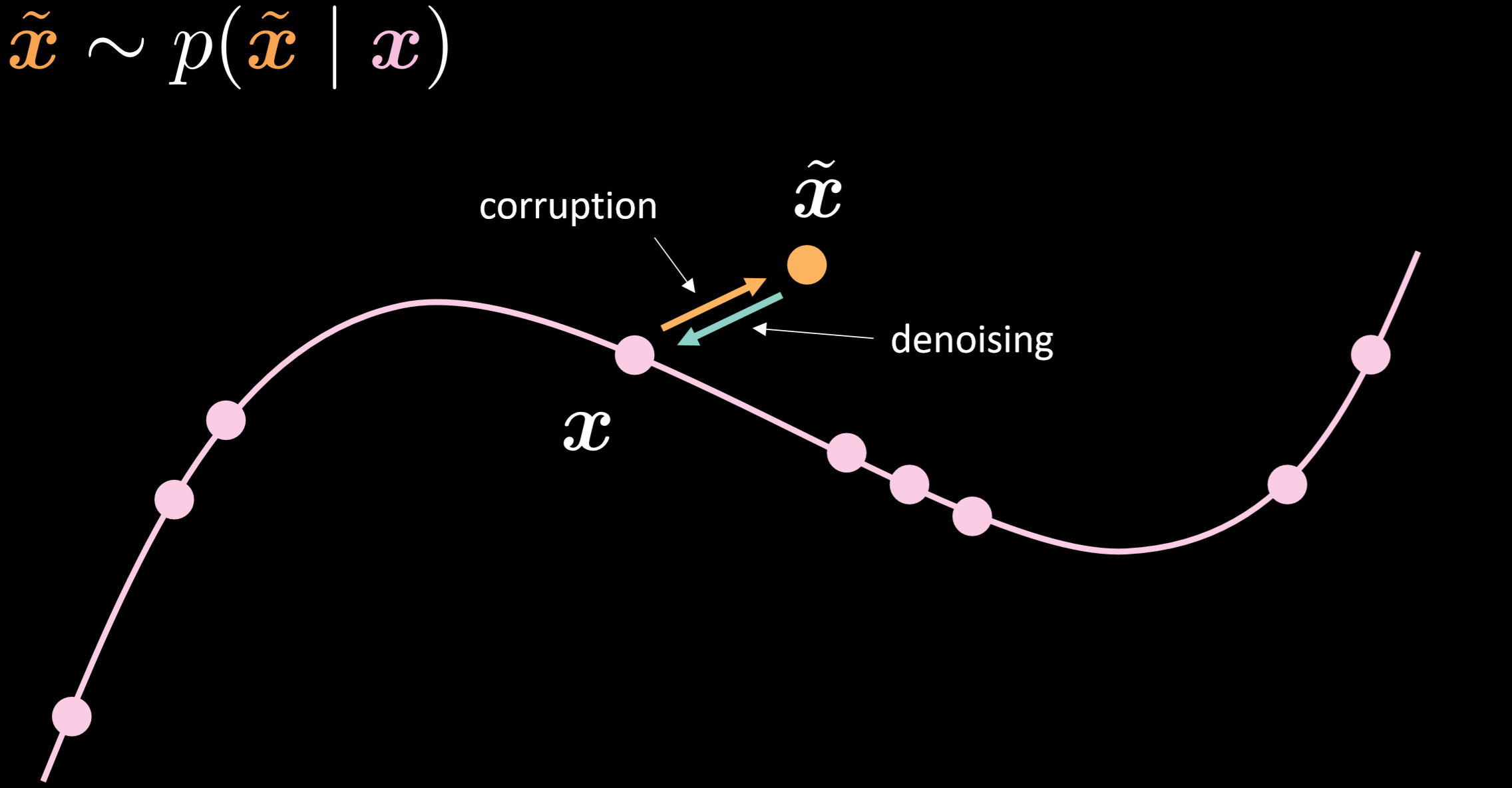
그림. 15: 노이즈 제거 오토인코더

이 모델에서는 현실에서 관찰되는 것과 동일한 잡음 분포^{noisy distribution}을 주입한다고 가정해서, 이를 통해 견고하게 복구하는 법을 배울 수 있도록 한다. 입력과 출력을 비교하면, 이미 매니폴드 데이터 위에 있는 포인트들은 움직이지 않았고, 매니폴드에서 멀리 떨어진 포인트들은 많이 움직인 것을 확인할 수 있다.

그림.16 은 입력 데이터와 출력 데이터 사이의 관계를 보여준다.

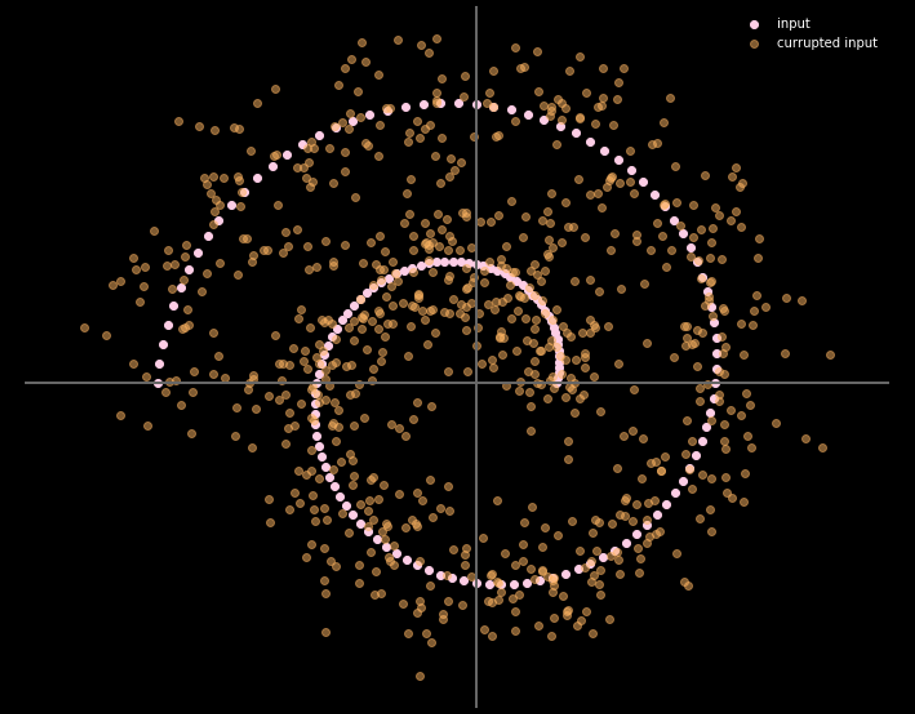
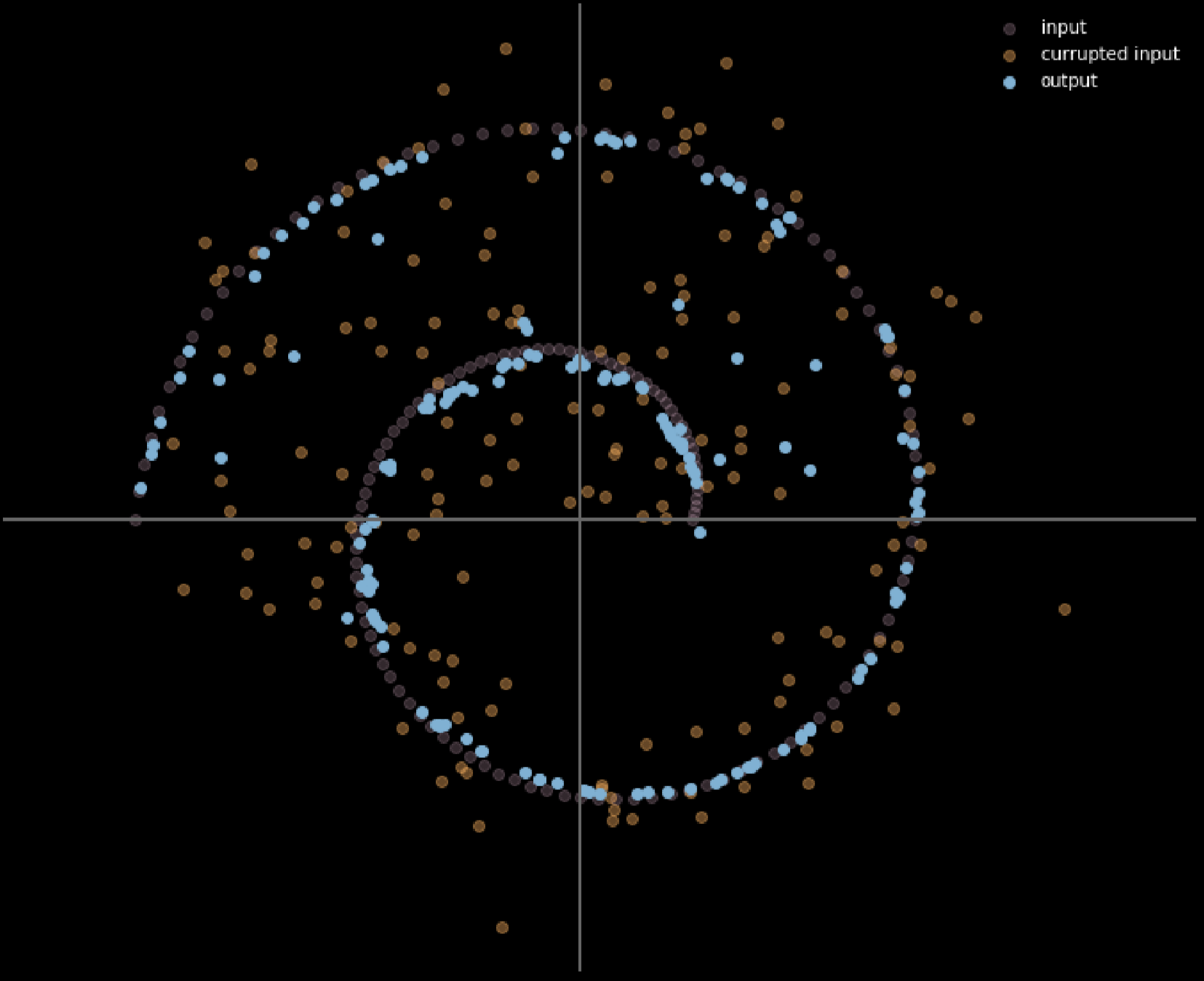
그림. 16: 노이즈 제거 오토인코더의 입력과 출력

또한 다른 색상을 사용해서 각 입력 포인트의 이동 거리를 나타낼 수 있다. 그림. 17은 이 다이어그램^diagram을 보여준다.

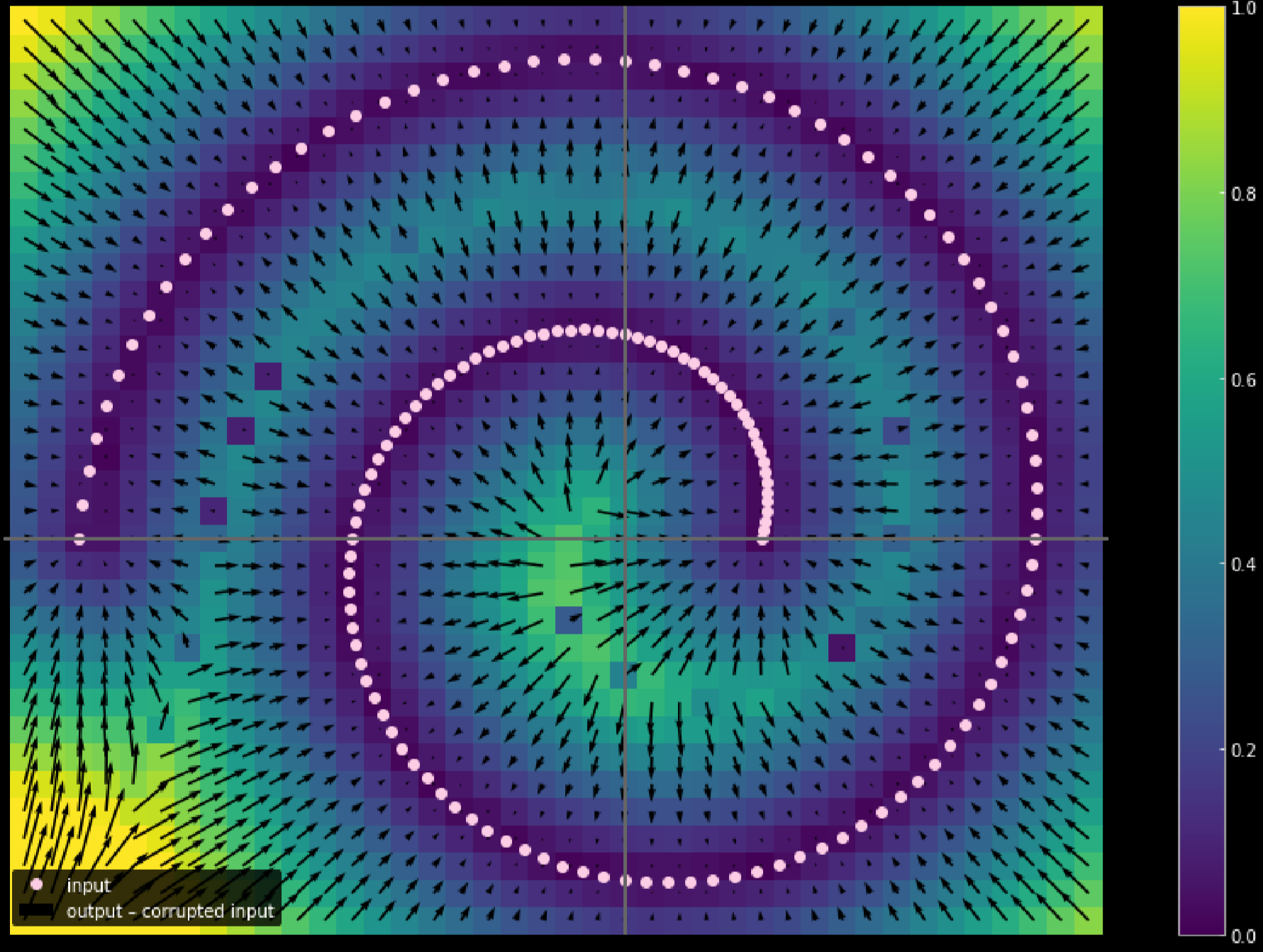
그림. 17: 입력 데이터의 이동 거리 측정

색상이 밝을수록, 데이터 포인트의 이동거리가 길어진다. 다이어그램에서 구석에 있는 점은 1 단위에 가깝게 이동한 반면, 2개 지점^branches 안의 데이터 포인트들은 훈련 과정 중에 위쪽 및 아래쪽 지점으로부터 끌어당겨^attracted지므로 전혀 움직이지 않았음을 알 수 있다.

수축형^Contractive 오토인코더

그림.18은 수축형 오토인코더의 손실 함수와 그 매니폴드를 보여준다.

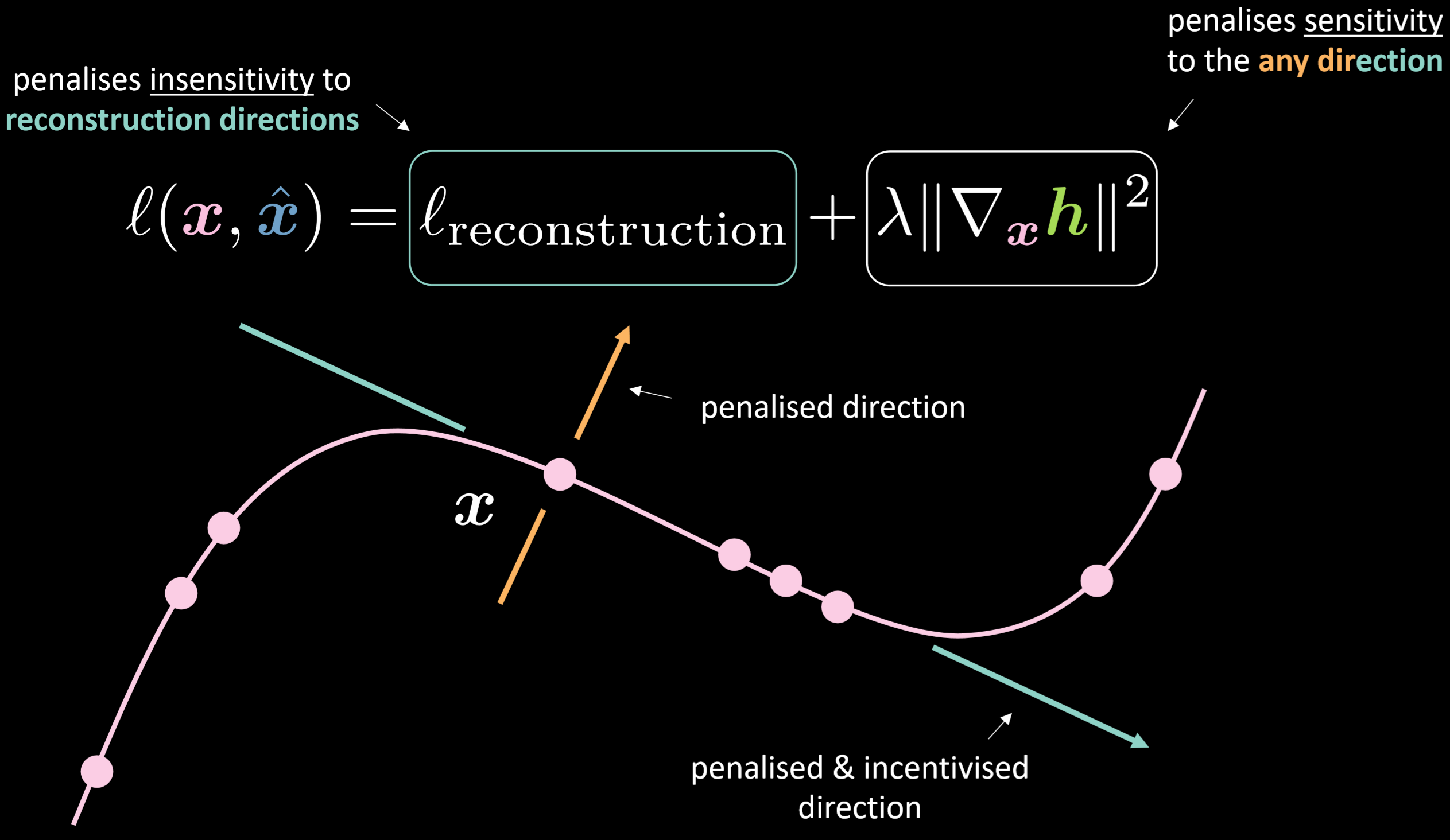
그림. 18: 수축형 오토인코더

손실 함수에는 재건^{reconstruction} 항에 입력에 대한 은닉 표현 그래디언트^gradient의 제곱 놈^norm을 더한 것이 포함된다. 따라서, 전체 손실은 입력의 변화에 따른 은닉층의 변화를 최소화한다. 이것의 이점은 모델이 재건의 방향에 대해 민감하게 반응하도록 하는 반면, 이 외의 다른 방향으로는 둔감하게 만든다는 것이다.

그림.19는 이러한 오토인코더가 일반적으로 어떻게 작동하는지 보여준다.

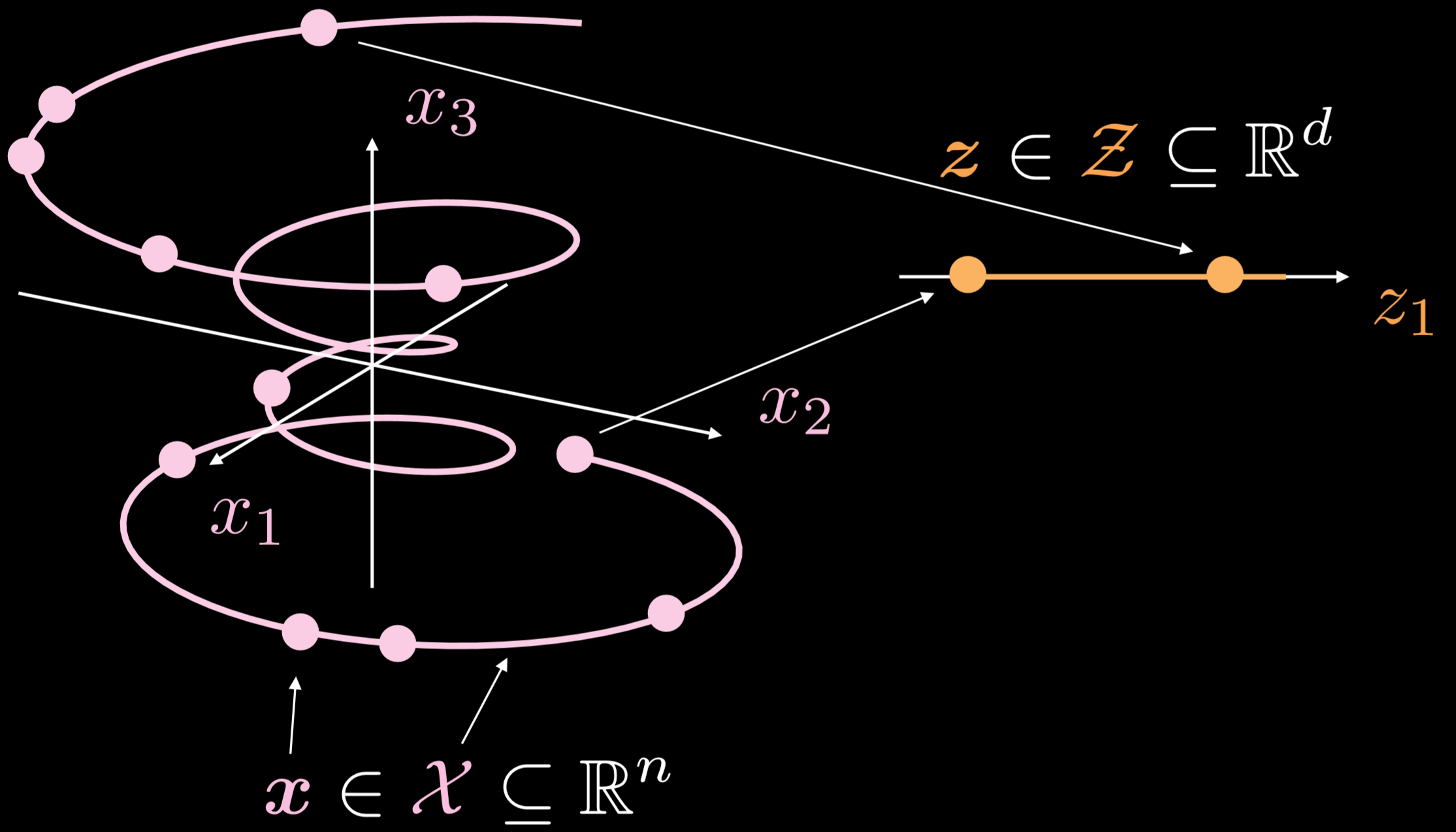
그림. 19: 기본 오토인코더

훈련 매니폴드는 3차원으로 진행하는 단일 차원^{single-dimensional} 개체이다. $\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$ 에서, 오토인코더의 목표는 구부러진 선을 \boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$ 에서 한 방향으로 펼치는 것이다. 결과적으로, 입력 레이어의 데이터 포인트가 잠재 레이어의 데이터 포인트로 변환된다. 이제 우리는 입력 공간의 데이터 포인트와 잠재 공간의 데이터 포인트 사이의 대응성^{correspondence}을 가지게 되었지만, 입력 공간과 잠재 공간의 영역 사이에는 대응성을 갖고 있지 않다. 다음으로, 디코더를 사용해서 잠재 레이어의 데이터 포인트를 변환해서 의미있는 출력 레이어를 생성한다.

오토인코더 구현 - 노트북

이에 대한 주피터 노트북은 여기에서 확인할 수 있다.

이 노트북에서는, 표준 오토인코더와 노이즈 제거 오토인코더를 구현하고 출력을 비교해본다.

오토인코더 모델 아키텍처 및 재건 손실 정의

$28 \times 28$ 이미지와 30-차원의 은닉층을 사용한다. 변환^{transformation} 과정은 $784\to30\to784$ 순서로 진행된다. 쌍곡 탄젠트^{hyperbolic tangent} 함수를 인코더와 디코더 과정에 적용해서 출력 범위를 $(-1, 1)$ 으로 제한할 수 있다. 평균 제곱 오차^{Mean Squared Error} (MSE) 손실이 해당 모델의 손실 함수로 사용된다.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

표준^Standard 오토인코더 훈련시키기

PyTorch를 사용하여 표준 오토인코더를 훈련시키려면 훈련 루프^loop에 다음의 5가지 방법을 넣어야 한다:

순방향 진행^{Going forward}:

1) output = model(img) 를 호출해서 모델을 통해 입력 이미지를 보낸다.
2) criterion(output, img.data) 를 사용해서 손실을 계산한다.

역방향 진행^{Going backward}:

3) optimizer.zero_grad() 값이 누적되지 않도록 그래디언트^gradient를 지운다.
4) 역전파^{Back propagation}: loss.backward()
5) 뒤로 이동^{Step backwards}(역주. 매개변수 업데이트): optimizer.step()

그림. 20은 표준 오토인코더의 출력을 보여준다.

그림. 20: 표준 오토인코더 출력

노이즈제거^Denoising 오토인코더 훈련시키기

노이즈제거 오토인코더의 경우, 다음의 단계를 추가해야 한다:
1) nn.Dropout() 를 호출해서 무작위로 뉴런을 끄기^{randomly turning off neurons}.
2) 노이즈 마스크^mask 생성하기: do(torch.ones(img.shape)).
3) 좋은 이미지^{good images}를 바이너리^binary 마스크에 곱해서 나쁜 이미지^{bad images} 만들기: img_bad = (img * noise).to(device).

그림. 21은 노이즈제거 오토인코더의 출력을 보여준다.

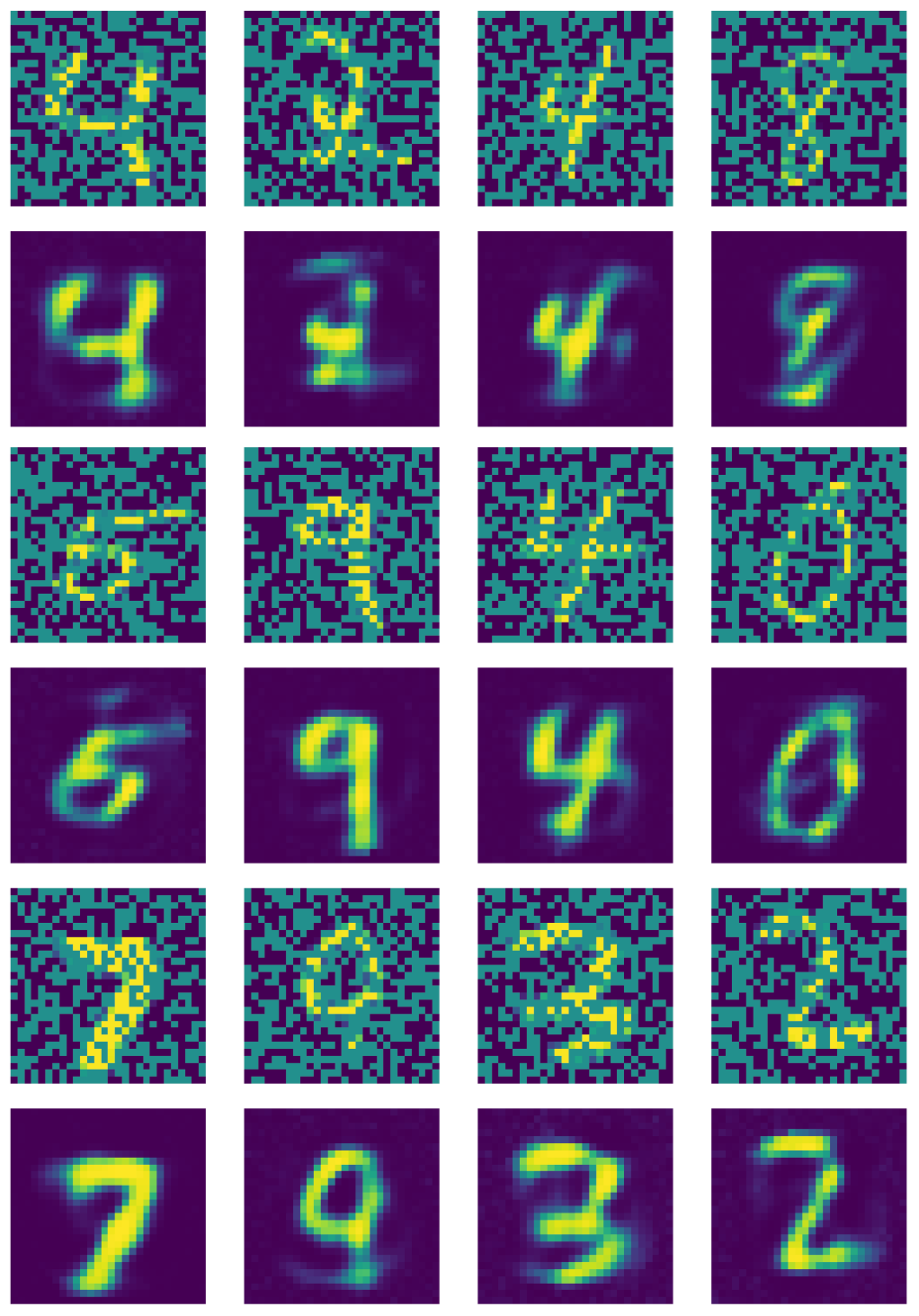
그림. 21: 노이즈제거 오토인코더의 출력

커널 비교^{Kernels comparison}

입력층의 차원이 $28 \times 28 = 784$ 임에도 불구하고, 이미지의 검은색 픽셀의 갯수 때문에 은닉층은 500 차원의 과잉-완전 층임을 알아둘 필요가 있다. 아래는 완전하지 않은^{under-complete} 표준 오토인코더에 사용되는 커널의 예시이다. 명확히 확인할 수 있듯이, 숫자가 있는 영역의 픽셀은 일종의 패턴의 감지를 나타내는 반면, 이 영역 바깥의 픽셀은 기본적으로 무작위이다. 이는 표준 오토인코더가 숫자가 있는 영역 외부의 픽셀에 관해서는 신경쓰지 않음을 나타낸다.

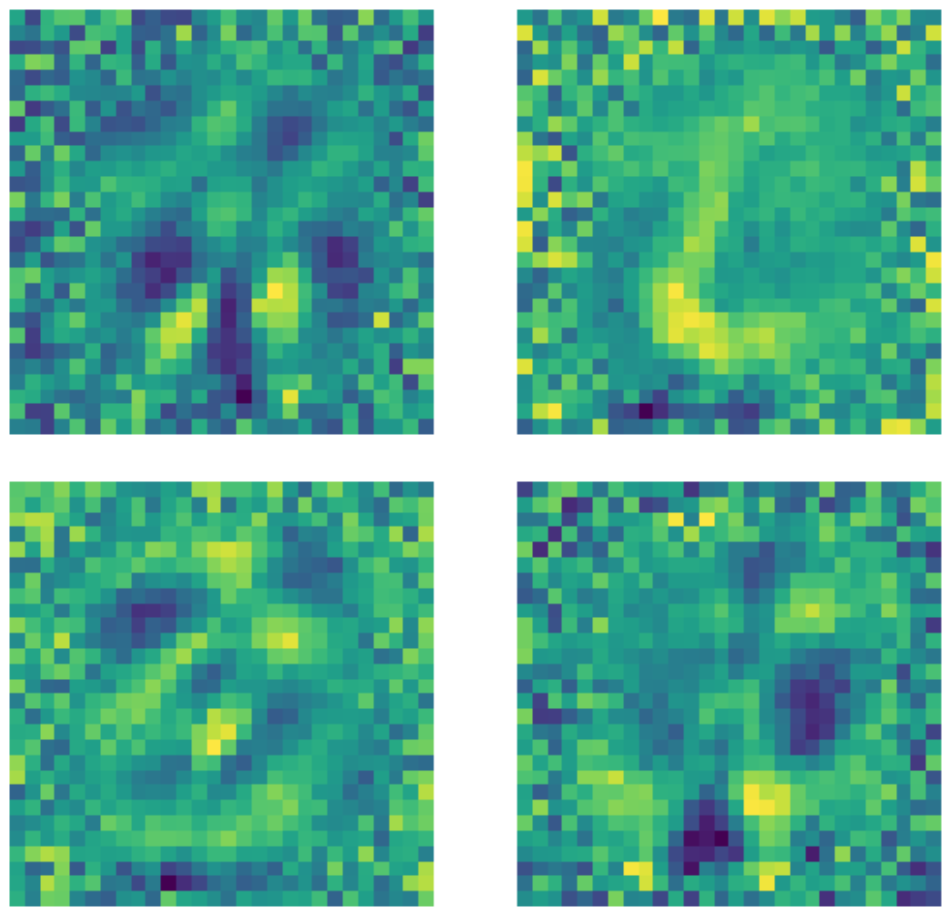
그림 22: 표준 AE 커널들.

반면에, 모델을 적합^fitting시키기 전에 드롭아웃 마스크를 각 이미지에 적용한 노이즈제거 오토인코더의 경우 다른 일이 발생한다. 패턴을 학습하는 모든 커널은 숫자가 존재하는 영역 외부의 픽셀을 일정한 값으로 설정한다. 드롭아웃 마스크가 이미지에 적용되자, 모델이 숫자 영역 외부의 픽셀까지 신경을 쓰게 된 것이다.

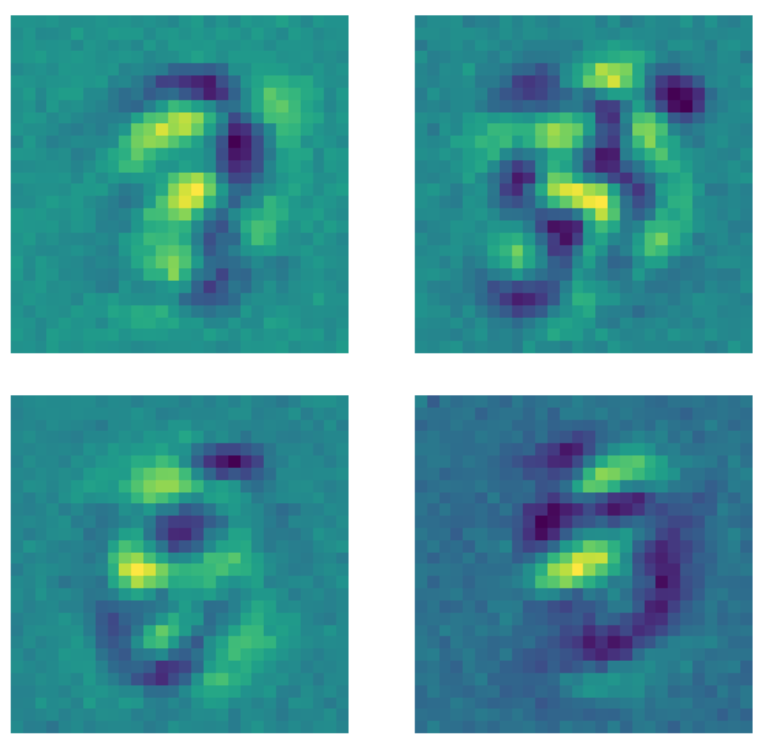
그림 23: 노이즈제거 AE 커널들.

가장 최신의 모델보다^{Compared to the state of the art}, 우리의 오토인코더가 실제로 더 작동한다!! 결과는 아래에서 확인할 수 있다.

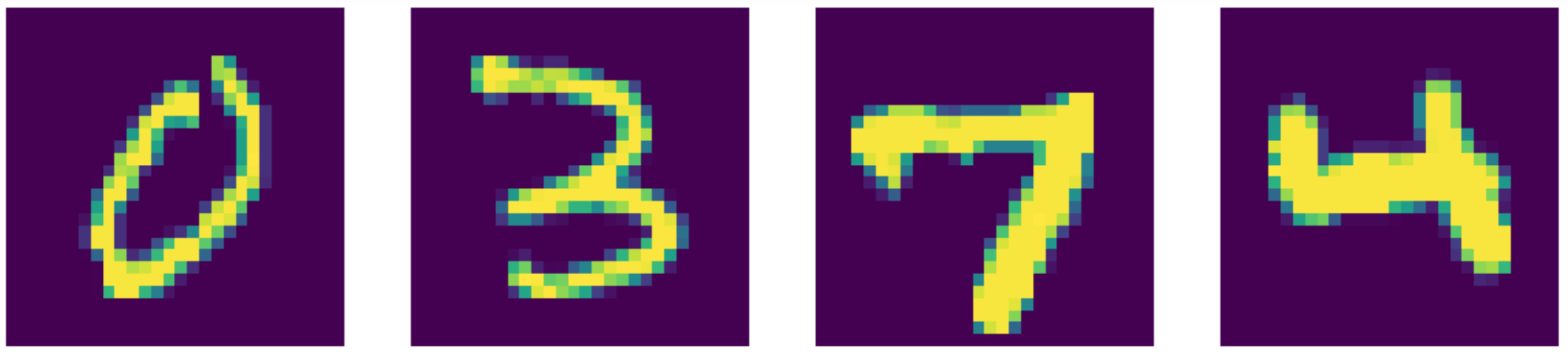
그림 24: 입력 데이터 (MNIST 숫자들).

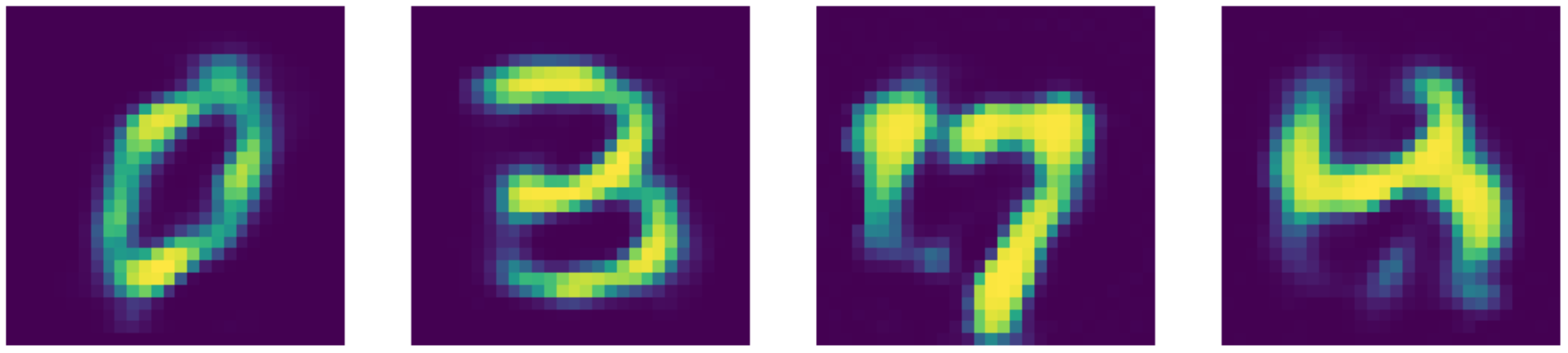
그림 25: 노이즈제거 AE 재건^{reconstructions}.

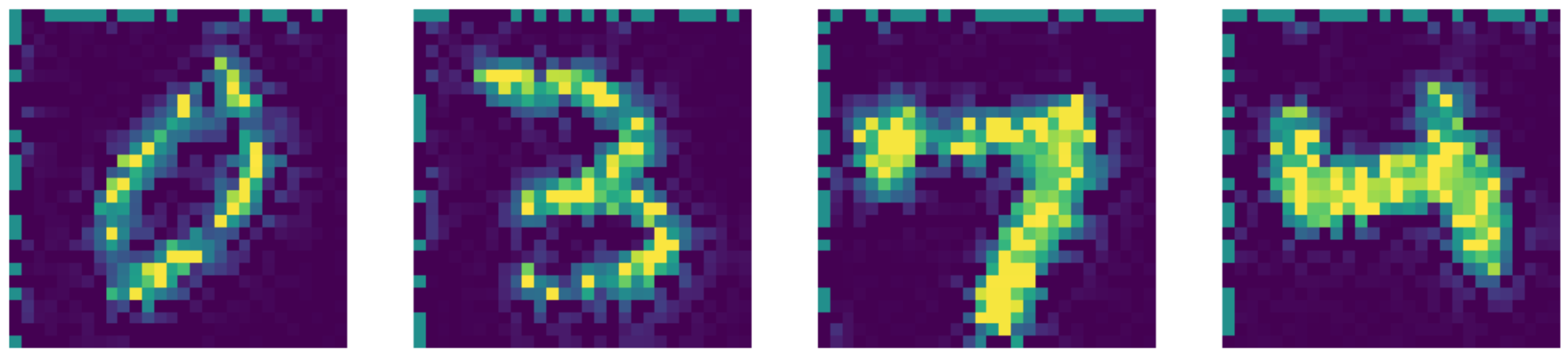
Figure 26: Telea inpainting output.

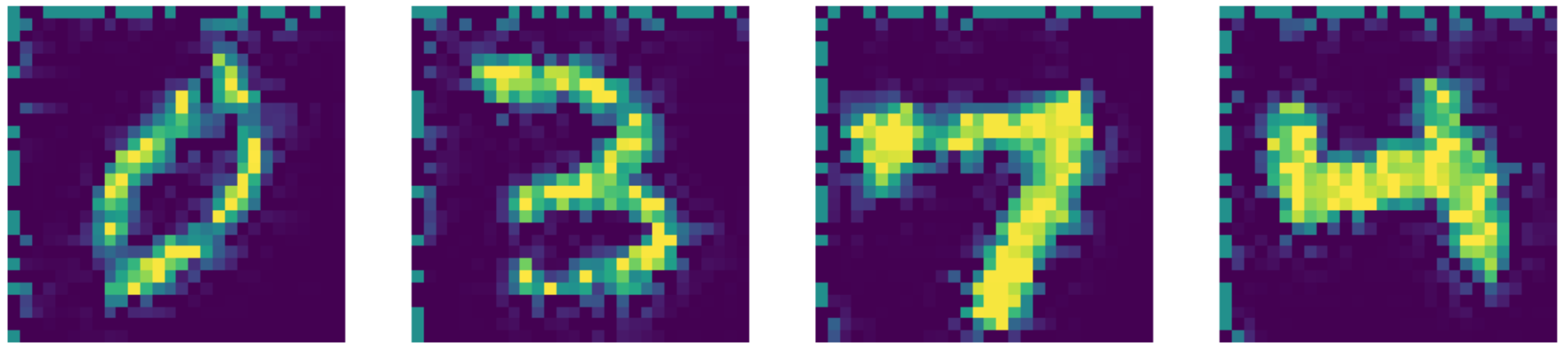
Figure 27: Navier-Stokes inpainting output.