세부 사항 및 예제가 포함된 SSL, EBM

자기 지도 학습 ^{Self Supervised Learning}

자기지도 학습은 지도학습과 비지도학습 모두를 포함한다. 자기지도 사전 텍스트 작업^{SSL pretext task}의 목적은 입력 데이터를 다시 잘 표현해 내고 이것을 이어지는 지도학습에서 사용할 수 있도록 하는 것이다. 자기지도 학습 모델은 데이터의 일부를 바탕으로 그 나머지를 예측하도록 훈련된다. 예를 들어, BERT는 자기지도 학습 기술을 이용해 학습되었고, Denoising Auto-encoder는 특히 자연어 처리 부문에서 최신의 성과를 보이고 있다.

그림. 1: 자기 지도 학습 ^{Self Supervised Learning}

자기지도 학습은 과제는 다음과 같은 작업으로 정의 할 수 있다:

• 과거로부터 미래를 예측하는 것.
• 보이는 것을 바탕으로 보이지 않는 것^{the masked}을 예측하는 것.
• 가용할 수 있는 모든 부분을 바탕으로 가려진 부분을 예측하는 것.

예를 들어, 카메라가 움직일 때 시스템이 다음 프레임을 예측하도록 학습되면, 이 시스템은 암묵적으로 깊이와 시간의 흐름에 대해 학습한다. 이는 시스템이 시야에서 사라진 물체가 사라지는 것이 아니라 지속적으로 존재한다는 것과 움직이는 물체와 움직이지 않는 물체 그리고 배경을 구분할 수 있도록 한다. 뿐만 아니라 중력과 같은 직관적인 물리학에 대해서도 학습하게 된다.

최신의 NLP 시스템 (BERT)은 거대한 신경망을 사전 학습^pre-train시키는 데에 자기지도 학습을 이용한다. 문장에서 일부 단어를 제거한 다음에 사전 학습 대상이 되는 시스템이 이 누락된 단어를 예측하도록 한다. 이는 매우 성공적이었다. 비슷한 아이디어가 컴퓨터 비전 분야에서도 시도되었다. 아래의 이미지에서 확인할 수 있듯, 이미지를 촬영하고 그 이미지 일부분을 제거한 다음 모델이 이렇게 누락된 부분을 예측하도록 학습시킬 수 있다.

그림. 2: 컴퓨터 비전 부문에서 활용된 예시 결과

컴퓨터 비전 부문에서 위와 같은 방식으로 학습된 모델이 누락 된 공간을 채울 수는 있었지만, NLP 시스템과 같은 수준의 성과를 이뤄내지는 못했다. 컴퓨터 비전 시스템에 대한 입력 값으로 이러한 모델에서 생성된 내부 표현을 사용한다면, 이 모델은 ImageNet에서 지도학습 방식으로 사전 학습된 모델을 이길 수 없다. 이 지점에서 NLP와 컴퓨터 비전 시스템 사이의 차이는 NLP는 이산적^discrete인 반면, 이미지는 연속적^continuous이라는 것이다. 이산 영역에서 우리는 불확실성을 표현하는 방법을 알고 있고, 가능한 출력에 대해 큰 소프트맥스^softmax값을 사용할 수 있지만, 연속적 영역에서는 그렇게 할 수 없기 때문에 각 시스템의 성과에 차이가 있었다.

지능형 시스템^{intelligent system} (AI 에이전트)은 지능적인 결정을 내리기 위해 주변 환경 및 자신에 대한 자체적인 행동의 결과를 예측할 수 있어야 한다. 우리를 둘러싼 세계가 완전히 결정론적이지 않고, 기계와 인간의 두뇌에는 모든 가능성을 설명할 수 있을 만큼의 컴퓨팅 파워가 없기 때문에 우리는 AI 시스템에게 고차원 공간 속의 불확실성 아래에서도 예측을 해 낼 수 있도록 훈련시켜야 한다. 이를 위해 에너지 기반^Energy-based모델이 굉장히 유용할 수 있다.

비디오의 다음 프레임을 예측하기 위해 최소 제곱^{Least Squares}을 사용해 학습된 신경망은 흐릿한 이미지 결과물을 만들어내는데, 이는 모델이 미래를 정확하게 예측할 수 없어서 이에 따른 손실값을 줄이기 위해 훈련 데이터에서 다음 프레임의 모든 가능성을 평균내 버리기 때문이다.

다음 프레임 예측을 위한 잠재 변수 에너지 기반 모델:

선형 회귀 분석과 다르게, 잠재 변수 에너지 기반 모델은 우리가 세계에 대해 알고 있는 것 뿐만 아니라 실제에서 일어난 일들에 대한 정보를 제공하는 잠재 변수를 사용한다. 이 두 가지 정보의 조합은 실제로 발생하는 것들에 가까운 예측을 해 내는데 활용될 수 있다.

이러한 모델은 시스템 에너지를 최소화하는 잠재 변수를 이용한 예측을 바탕으로 입력 $x$ 와 실제 출력 $y$ 사이의 호환성을 평가하는 시스템으로 생각할 수 있다. 압력 $x$ 를 관찰하고 이 입력 $x$ 와 잠재 변수들 $z$ 과의 다양한 조합을 이용해 예측값 $\bar{y}$ 를 생성하여 시스템의 에너지, 예측 오류를 최소화 하는 것을 선택한다.

뽑아내는 잠재 변수에 따라 우리는 가능한 모든 예측값을 얻을 수 있다. 잠재 변수는 입력 $x$ 에 없는 출력 $y$ 와 관련된 중요한 정보로 간주할 수 있다.

스칼라 값^scalar-value 에너지 함수는 두 가지 버전을 가진다:

1. 조건부^conditional $F(x, y)$ - $x$ 와 $y$ 사이의 호환성을 측정
2. 무조건부^{unconditional} $F(y)$ - $y$ 의 구성 요소 사이의 호환성 측정

에너지 기반 모델 학습시키기:

$F(x, y)$ 를 매개변수화 하기 위한 에너지 기반 모델을 훈련시키는 두 개의 학습 모델 클래스가 있다.

1. 대조적^Contrastive 방법: $F(x[i], y[i])$ 을 밀어 내리고, 다른 점들 $F(x[i], y’)$ 을 밀어 올리는 것
2. 구조적^{Architectural} 방법: 낮은 에너지 영역의 크기가 정규화를 통해 제한되거나 최소화되는 $F(x, y)$ 를 만들어내는 것

에너지 함수를 형성하는 일곱개의 전략이 있다. 대조적 방법은 밀어 올릴 점들을 골라내는 방식에서 차이가 발생한다. 반면 구조적 방법은 코드의 정보 용량을 제한하는 방식에서 차이가 있다.

대조적 방법의 예시는 최대 우도 학습^{Maximum Likelihood learning}이다. 에너지는 표준화되지 않은 음의 로그 밀도 함수로 간주될 수 있다. 깁스 분포^{Gibbs distribution} 는 x 가 주어진 상태에서 y 의 우도^likelihood 를 제공한다. 이는 다음과 같은 식으로 표현될 수 있다:

\(P(Y \mid W) = \frac{e^{-\beta E(Y,W)}}{\int_{y}e^{-\beta E(y,W)}}\)

최대 우도는 분자를 크게하고, 분모를 작게해서 우도 값을 최대화 하고자 한다. 이는 아래에서 주어진 것과 같이 $-\log(P(Y \mid W))$ 을 최소화 하는 것과 같다.

하나의 샘플 Y에 대한 음의 로드 우도 손실^{negative log likelihood loss}의 경사값은 다음과 같다:

위의 경사값에서, 데이터포인트 $Y$ 의 경사값에서의 첫 번째와 두 번째 항은 전체 $Y$s 에 대한 에너지 기댓값을 제공한다. 즉, 우리가 경사 하강법을 적용할 때 첫 번째 항은 주어진 데이터포인트 $Y$에 대해서 에너지를 줄이려고 하고, 두 번째 항은 다른 모든 $Y$s 를 바탕으로 에너지를 증가시키려고 한다.

에너지 함수의 기울기는 대체로 매우 복잡하고, 따라서 이것의 적분을 계산하고, 추정하고, 근사하는 것은 대부분의 경우 다루기가 어려워서^intractable 굉장히 흥미로운 케이스가 된다.

잠재 변수 에너지 기반 모델

잠재 변수 모델의 주요 장점은 잠재 변수를 이용한 다양한 예측이 가능하다는 것이다. $z$ 가 어떤 집합 안에서 변함에 따라, $y$ 는 가능한 예측값을 원소로 하는 매니폴드(다양체)^manifold 에서 변화한다. 이에 대한 몇가지 예는 다음과 같다:

1. K-means
2. 희소 데이터 모델링^{Sparse modeling}
3. GLO

이는 아래의 두 종류 중 하나이다:

1. $y$ 가 $x$ 의 종속 변수인 조건부^conditional 모델
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. y 사이의 호환성을 측정하는 스칼라 값의 에너지 함수 F(y), 무조건부^{unconditional} 모델
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

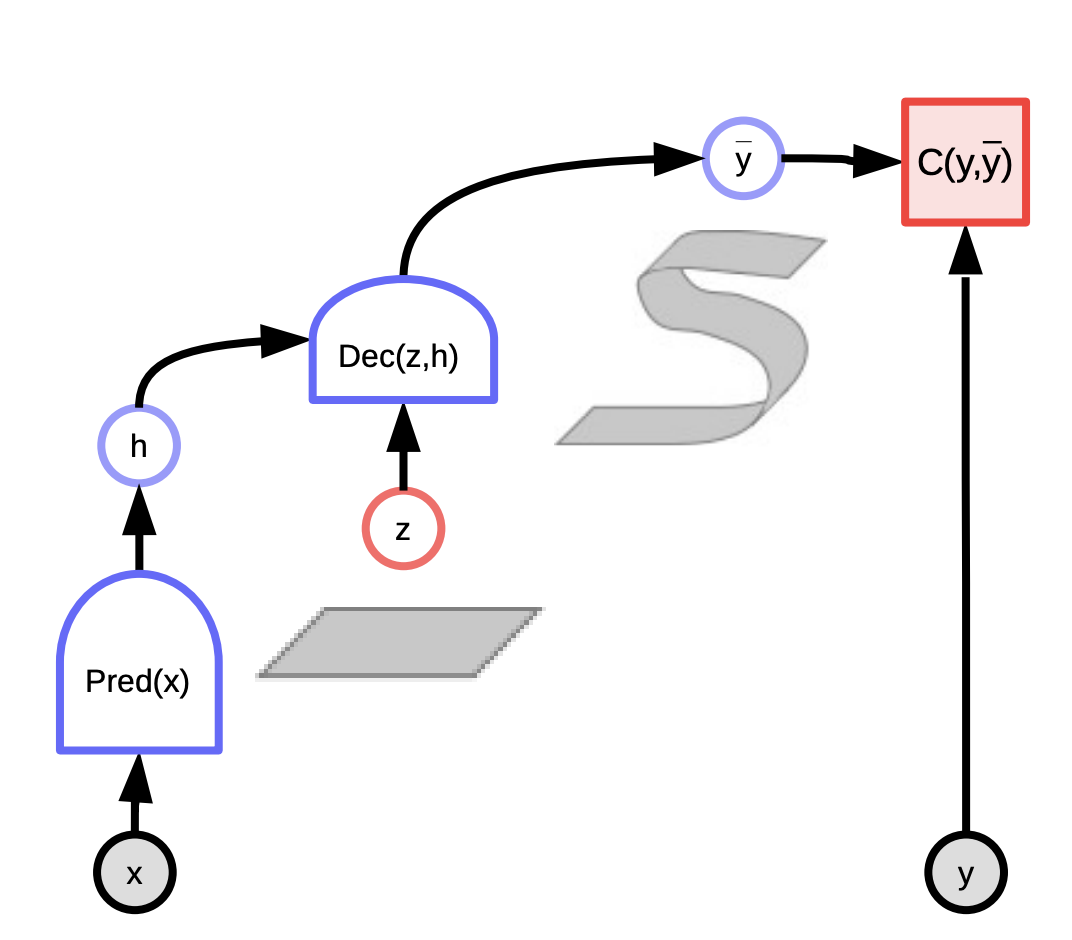
그림. 3: 잠재 변수 EBM

잠재 변수 EBM 예시: K-means

K-means는 간단한 클러스터링 알고리즘으로써 $y$ 의 분포르 모델링 하려 하는 에너지 기반 모델로도 간주될 수 있다. 에너지 함수는 $z$ 가 원-핫^one-hot 벡터인 $E(y,z) = \Vert y-Wz \Vert^2$ 이다.

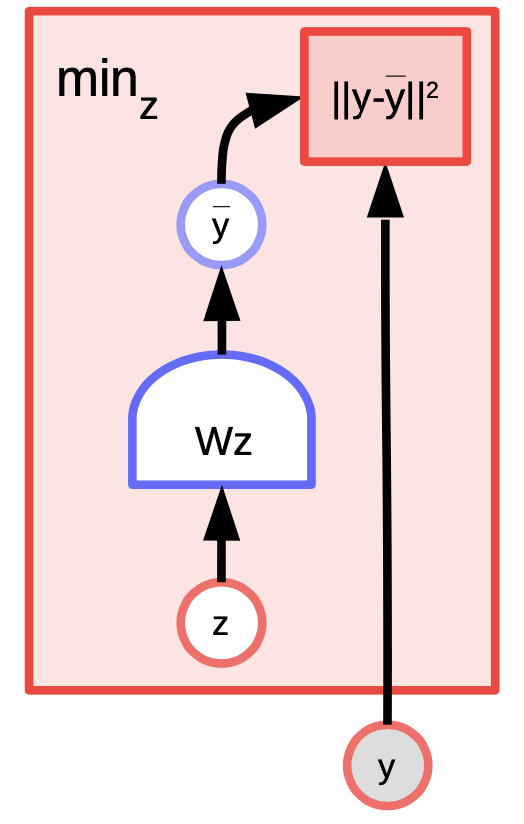
그림. 4: K-means 예시

$y$ 와 $k$ 값이 주어지면, $W$ 의 어떤 $k$ 개 가능한 열^columns 들이 재구성^{reconstruction} 오류 혹은 에너지 함수를 최소화 하는지 파악하여 추론할 수 있다. 알고리즘 훈련을 위해서, $z$ 를 찾아서 $y$ 와 가장 가까운 $W$ 의 열을 선택하고 여기서 경사하강법^GD을 수행하고 이 과정을 반복하여 목표하는 최솟값으로 더 가까이 접근하는 방식을 채택할 수 있다. 그러나, 좌표^coordinate 경사 하강법은 실제로 더 빠르고 효과적으로 작동한다.

아래의 그림에서 분홍색 나선 주변의 데이터 포인트를 관찰할 수 있다. 이 선을 둘러싼 검은 얼룩 자국은 W에 따른 각 프로토타입 모델 주변의 quadratic wells에 해당한다.

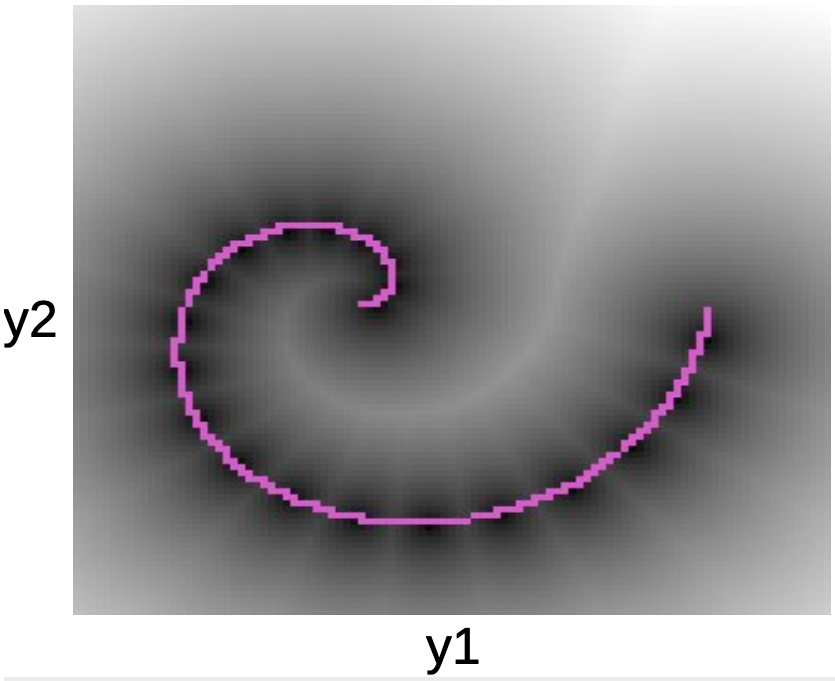
그림. 5: 나선형 그림

에너지 함수에 대해 알게되면, 다음과 같은 질문에 대해 답을 할 수 있게된다:

1. $y_1$ 의 점이 주어졌을 때, $y_2$ 를 예측해 낼 수 있는가?
2. $y$ 가 주어졌을 때, 이 데이터 매니폴드^manifold 와 가장 가까운 점을 찾아낼 수 있는가?

K-means 는 (대조적 방법과 반대인) 구조적 방법에 속한다. 따라서 우리는 에너지를 아무데나 밀어 올리지 않고, 특정 지역의 에너지를 낮춘다. 한 가지 단점은 $k$ 의 값이 결정되면, 에너지 값이 $0$ 인 데이터 포인트가 단 $k$ 로 한정된다는 것과, 다른 모든 포인트의 에너지 값은 그 데이터 포인트에서 멀어질수록 이차적으로^{quadratically} 증가하는 높은 값을 갖는다는 점이다.

대조적 방법

얀 르쿤 박사에 따르면 모든 사람이 언젠가는 구조적 방법을 사용할 것이지만, 현 시점에서는 이미지 데이터에 대해 잘 동작하는 것은 대조적 방법이다. 에너지 표면의 윤곽^contours과 데이터 포인트들을 보여주는 아래 그림을 참고하자. 이상적으로, 우리는 에너지 표현이 데이터 매니폴드 위에서 최소의 에너지를 갖기를 바란다. 따라서 에너지 훈련 예제 주변의 에너지 값 (즉, F(x,y)의 값) 을 낮추려고 하지만 , 이것 만으로는 충분하지 않을 수 있다. 따라서 높은 에너지값을 가져야 하는데 낮은 에너지값을 가지고 있는 부분의 $y$ 값을 올린다.

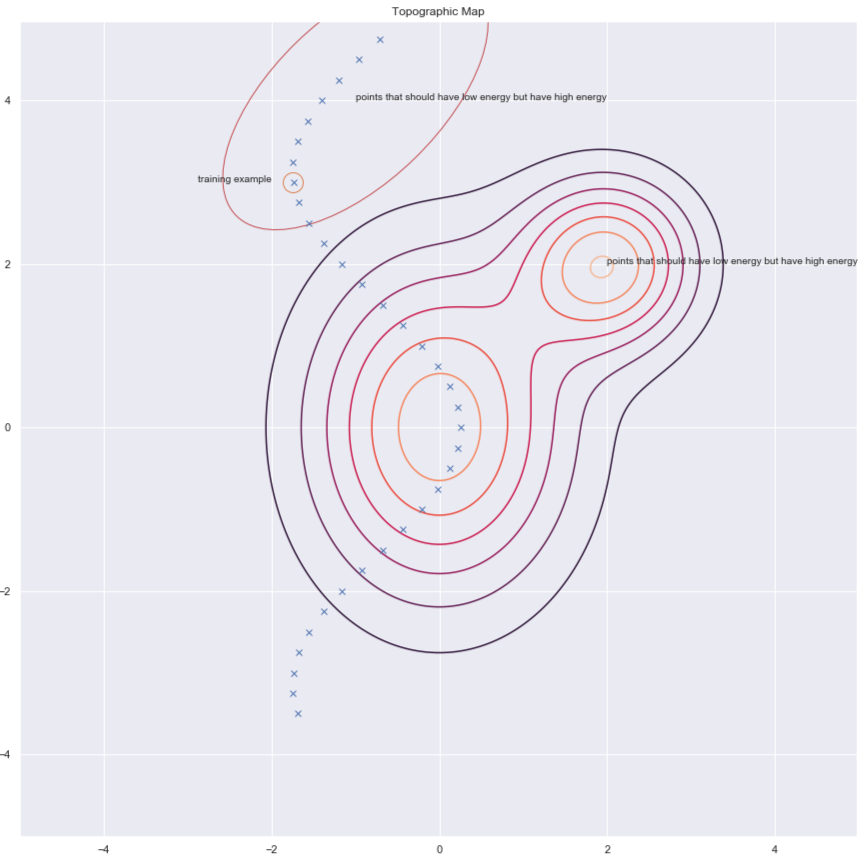
그림. 6: 대조적 방법

우리가 에너지 값을 높이고자 하는 $y$ 후보들을 찾는 몇 가지 방법이 있다. 이 방법의 몇 가지 예시는 다음과 같다:

1. Denoising Autoencoder^{디노이징 오토인코더}
2. Contrastive Divergence^{대조 발산}
3. 몬테 카를로^{Monte Carlo}
4. 마르코프 체인 몬테 카를로^{Markov Chain Monte Carlo}
5. 해밀토니안 몬테 카를로^{Hamiltonian Monte Carlo}

Denoising Autoencoders와 Constrasive Divergence에 대해 간단히 설명하겠다.

Denoising Autoencoder (DAE)

$y$ 를 찾는 방법 중의 하나는 아래의 그림에서 녹색 화살표로 표시된 것과 같이 훈련 예제 무작위로 교란시켜 에너지를 높이는 것이다.

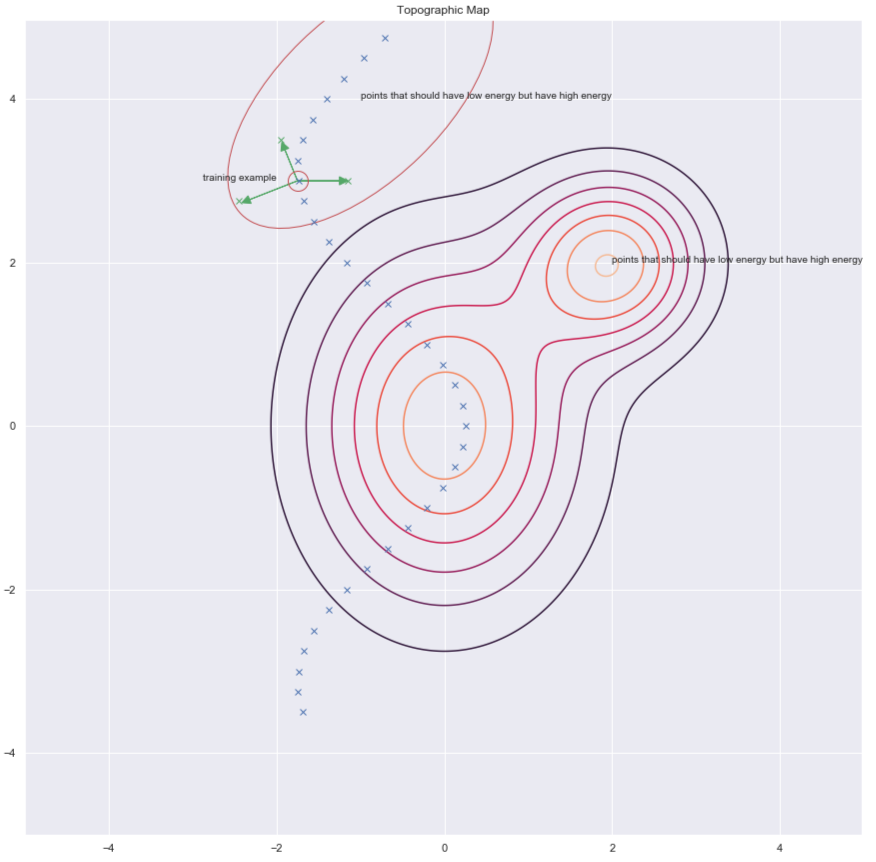
그림. 7: 지형도^{Topographic map}

데이터 포인트가 손상되면^corrupted, 에너지를 여기로 올릴 수 있다. 이러한 작업을 모든 데이터 포인트에 대해서 충분히 많은 횟수로 실행하면, 에너지 샘플이 훈련 예제를 중심으로 모인다. 이어지는 그림은 이 훈련이 어떻게 이뤄지는지 보여준다.

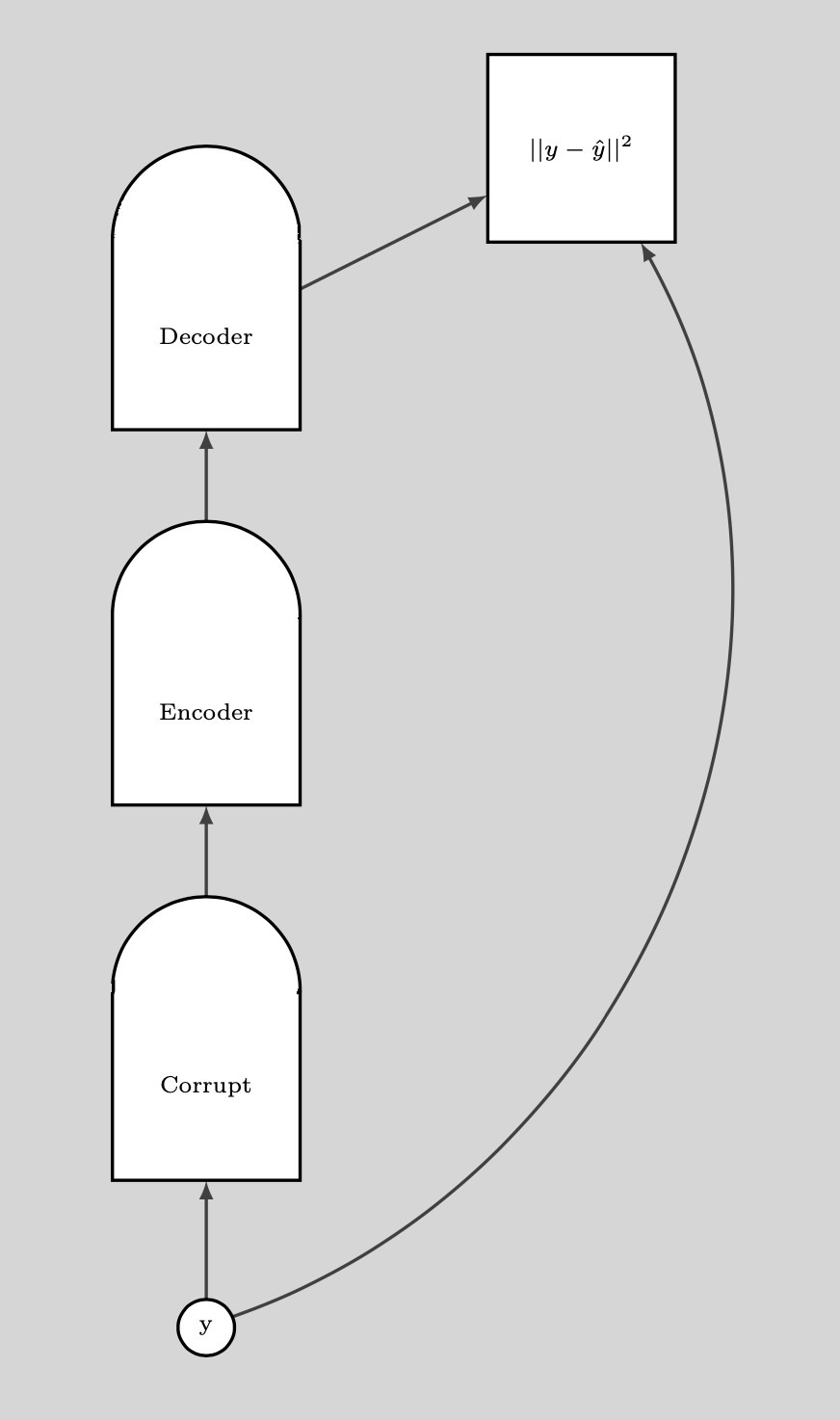
그림. 8: 훈련 과정

훈련 단계:

1. $y$ 점을 하나 잡고 이것을 손상시킴
2. 이렇게 손상된 데이터 포인트에서 원본 데이터를 재구성해 낼 수 있도록 인코더^Encoder와 디코더^Decoder를 훈련시킴 만일 DAE 이 올바르게 훈련 되면, 데이터 매니폴드에서 멀어짐에 따라 에너지 값이 2차적으로^{quadraticallly} 증가한다.
   The following plot illustrates how we use the DAE.

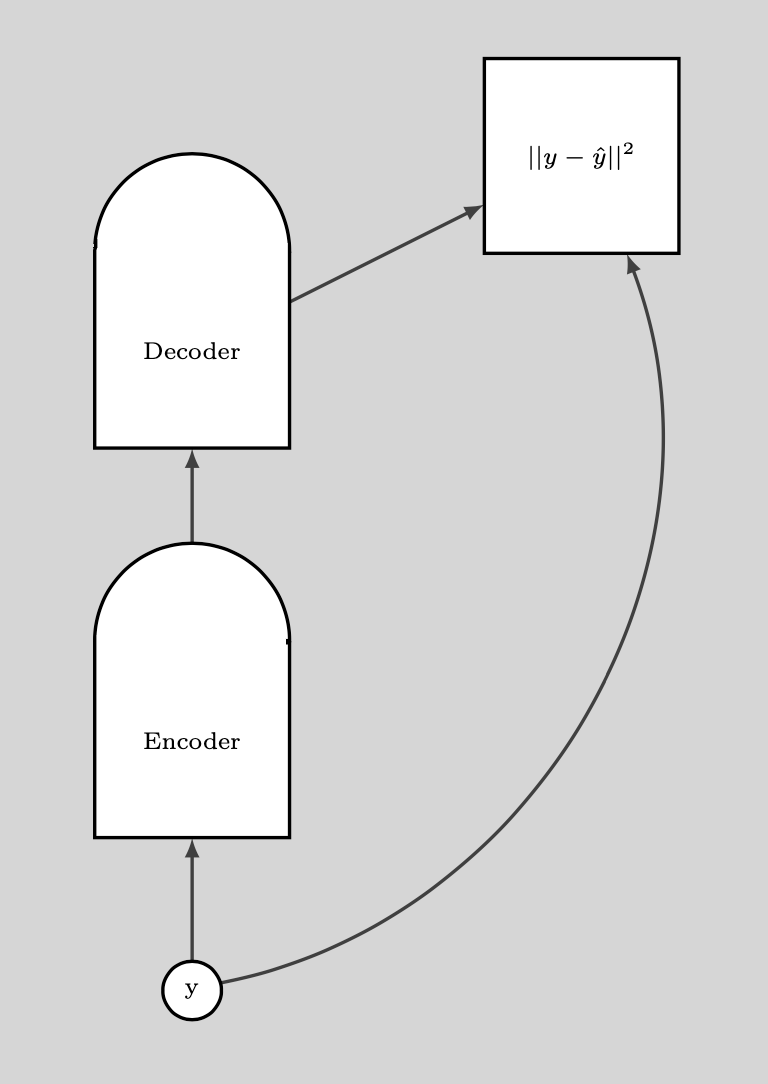
그림. 9: DAE가 이용되는 방식

BERT

BERT 는 텍스트를 이산적인 공간에서 처리하였다는 점을 제외하면 비슷한 방식으로 훈련되었다. 손상 기법^{the corruption technique}은 일부 단어를 가리고^masking 재구성 단계에서 이를 예측하는 방식으로 구성된다. 따라서 이는 masked autoencoder^{마스킹된 오코인코더}라고도 부른다.

Contrastive Divergence

Contrastive Divergence 는 우리가 에너지를 끌어올리고자 하는 $y$ 를 더 똑똑하게 찾는 방법을 제시한다. 훈련 지점에 임의의 킥^kick을 주고 경사 하강법을 이용해 에너지 함수를 낮춘다. 궤도의 끝에서, 우리가 착지하는 지점의 에너지 값을 증가시킨다. 이 과정은 아래의 그림에서 녹색 선을 통해 표현된다.

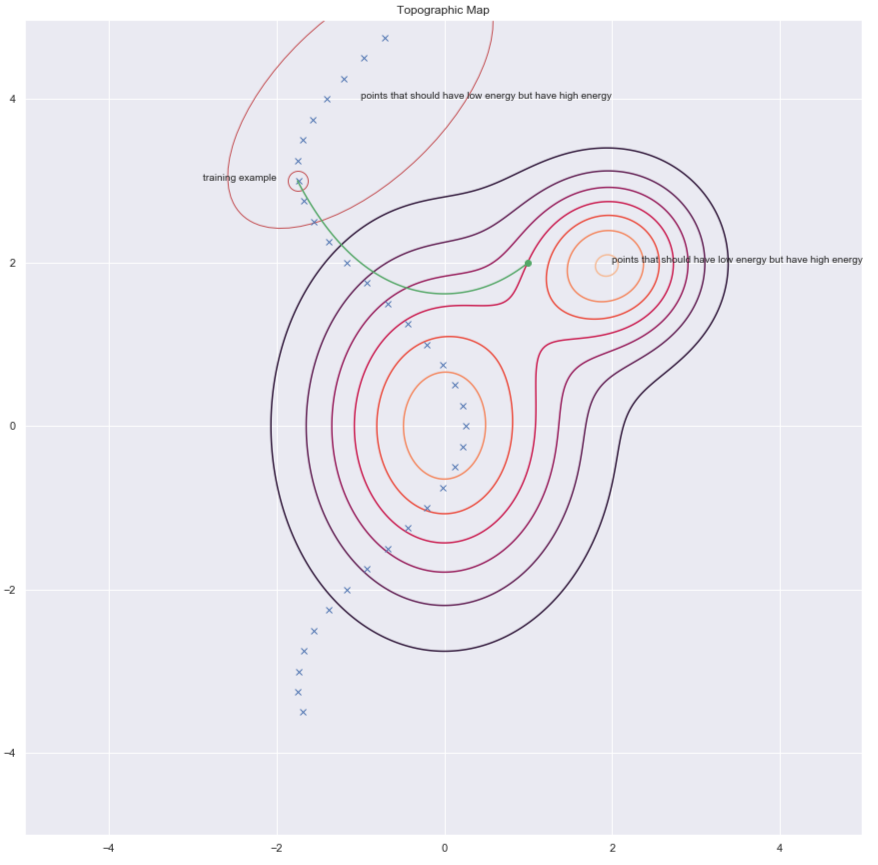
그림. 10: Contrastive Divergence