Energy-Based Models

개요

이 문서는 모델 정의에 새로운 방식을 소개한다. 에너지 기반 모델^{energy-based model}은 한데 아울러 지도^supervised, 비지도^unsupervised, 자기지도^{self-supervised} 모델을 정의하는데 도움을 주고, $x$ 변수들을 바탕으로 $y$ 값들을 출력한다. 피드 포워드 신경망^{feed-forward nets}에는 2가지의 주요 문제점이 있다:

1. 만약 추론^inference 과정이 여러곂의 가중합^{weighted sums} 보다 더 복잡한 계산이라면 어떻게 될까?
2. 만약 하나의 입력값이 여러개의 출력값을 가질수 있다면 어떻게 될까? 예: 비디오의 미래 프레임 예측. 기본적으로 분류^{classification} 신경망에서 우리는 이 신경망을 각 부류별로 스코어^score를 발산함을 위해 학습시킨다. 하지만, 이는 사진과 같은 연속적 고차원 정의역^{continuous high dimensional domain}에는 가능하지 않으며 (사진에는 소프트맥스^softmax를 적용할 수 없다!) 출력값이 이산적^discrete이여도 굉장히 큰 표본공간^{sample space}을 가질 수 도 있다. 예를 들어, 문서는 크나큰 수의 조합^combinations을 이루고 있으며, 에너지 기반 모델은 위와 같은 양상들을 모델하는데 더 나은 체계를 제시한다.

에너지 기반 모델 접근법

에너지 기반 모델은 $x$에서 $y$를 분류하는 것 보다, 특정 ($x$, $y$)의 짝들이 서로 맞는지 아닌지를 예측한다. 다시 말해, $x$에 양립하는 $y$를 찾는 것이다. $F(x,y)$가 낮은 $y$를 찾으며 우리는 문제를 제기할 수 있다. 예를 들어,

• $y$는 $x$의 정확한 고해상도 이미지인가?
• 문서A는 문서B의 좋은 번역문인가?

정의

에너지 기반 모델은 다음과 같이 정의된다: $F: \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$ 이며 $F(x,y)$가 $(x,y)$의 의존도^dependency를 설명한다 . (이 에너지는 추론에 는 사용되지만 학습에 사용되지 않는다는 것을 주목.) 추론은 다음 공식과 같이 주어진다: \(\check{y} = \displaystyle \text{argmin}_y \left \{ F(x,y)\right \}\)

해결책: 경사도 기반 추론^{gradient-based inference}

에너지 함수는 매끄럽고^smooth 미분 가능한 함수여야 경사도-기반 방법을 추론에 사용할 수 있다. 추론을 실행하기 위해서, 이 함수를 기울기하강^{gradient descent}을 이용해 양립적인 $y$를 찾는데 검색한다. 이 외에도 극소값을 얻기 위한 많은 다른 경사도 기법들이 있다. 여담: 그래프 모델은 에너지 기반 모델의 특수한 경우이다. 에너지 함수는 에너지 항들의 합으로 분해가 되는데, 각 에너지 항들은 우리가 사용하는 일부 변수들을 설명한다. 에너지 함수가 특정 구조로 짜여진다면, 우리가 추론 하고자 하는 에너지 항들의 최소합을 찾는 효율적인 추론 알고리즘들이 존재한다.

잠재변수를 가진 에너지 기반 모델

출력값 $y$는 $x$와 우리가 값을 모르는 추가 변수 $z$ (잠재변수)에 의해 결정되며, 이 잠재변수^{latent variable}는 보조정보^{auxiliary information}를 제공한다. 예로, 잠재변수는 글뭉치 사이사이 각 단어들의 경계를 알려줄 수 있고, 이는 사람들의 띄어쓰기 없는 손글씨를 해석하는데 큰 도움이 된다. 또한, 프랑스어와 같이 각 단어들의 사이가 미세하여 단어 사이를 해독하기 어려운 언어들을 해독하는데에도 매우 유용하다. <!–

Inference

To do inference with latent variable EBM, we want to simultaneously minimize energy function with respect to y and z.

And this is equivalent to redefining the energy function as: \(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\), which equals to: \(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z))\). When $\beta \rightarrow \infty$, then $\check{y} = \text{argmin}_{y}F(x,y)$. –>

추론

잠재변수를 가진 에너지 기반 모델을 추론하기 위해서는 에너지 함수를 y와 z에 대하여 동시에 최소화 해야한다.

그리고 이는 에너지 함수를 다음과 같이 재정립하는 것과 같다: \(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\) 이것은 다음과 같다\(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z))\) $\beta \rightarrow \infty$ 일때, $\check{y} = \text{argmin}_{y}F(x,y)$.

잠재변수를 허용하는 또 다른 큰 장점은 잠재변수를 변화시킴으로써 예측 출력값 $y$를 가능한 예측값 다양체^manifold 에 따라 변화 가능하게 만드는 것이다 (아래 그래프에서 보여지는 리본): $F(x,y) = \text{argmin}_{z} E(x,y,z)$.

이는 기계가 단 한 가지의 결과값이 아닌 여러가지의 출력값을 갖는 것을 가능케한다.

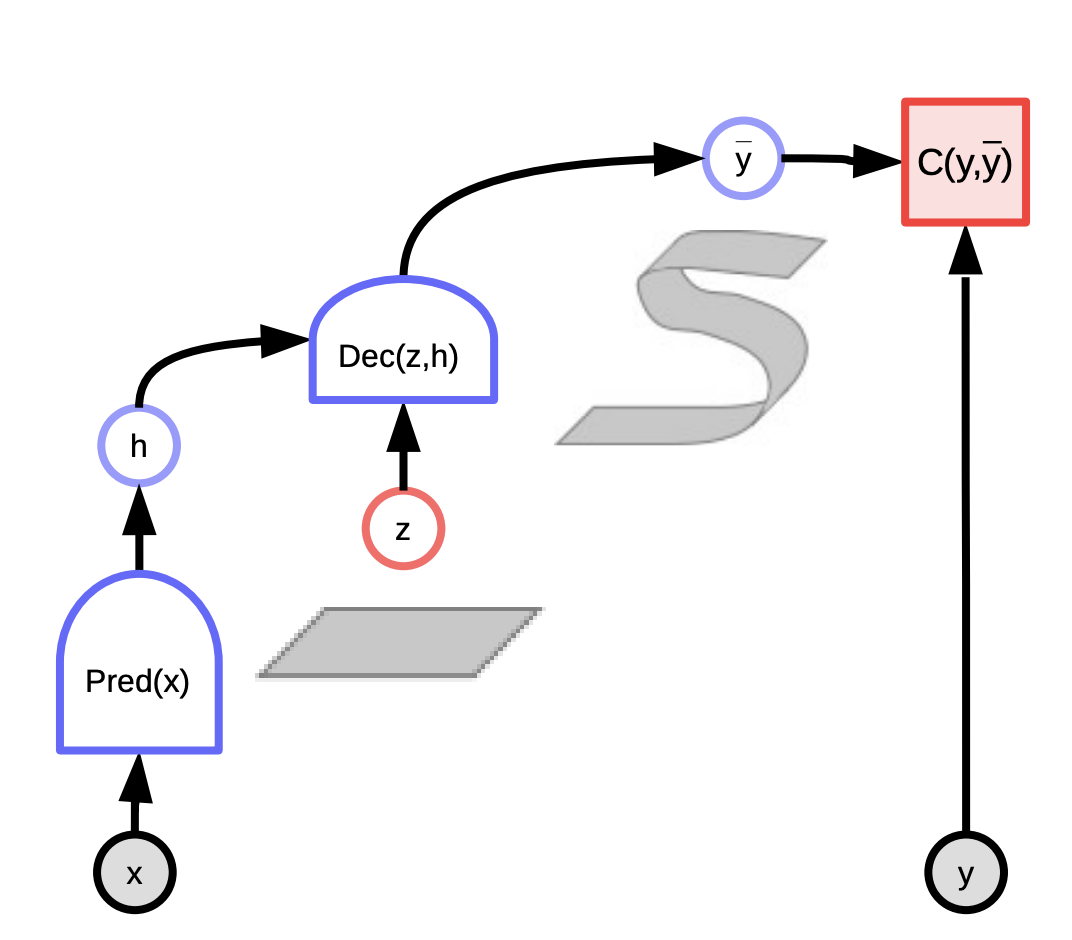
Fig. 1: 에너지 기반 모델의 산출 그래프

예제

한 예로 비디오 예측이 있다. 비디오 예측을 사용하기에 좋은 응용법이 많이 있는데, 그 중 하나는 비디오 압축 시스템이고, 다른 하나는 자율 주행 차에서 찍힌 비디오를 사용하여 다른 차들이 어떻게 행동할지 예측하는 것이다.

또 다른 예는 번역이다. 한 언어를 다른 언어로 번역하는 것은 하나의 명확한 답이 존재하는 것이 아니여서, 언어 번역은 항상 어려운 문제로 남아있다. 대게 같은 생각을 표현하는 데에는 여러가지의 방법이 존재하며 사람들은 왜 다른 방식을 택하지 않고 자신들이 표현하는 방식을 선택하였는지 설명하는 것에 어려움을 느낀다. 그러므로 주어진 문서에 시스템이 모든 가능한 번역문을 매개변수화하는 방식은매우 유용하다. 예를 들어, 독일어를 영어로 번역한다고 했을 때, 영문으로된 적절한 다수의 변역문이 있을 수 있고, 특정 매개변수를 변화시킴으로 번역문을 변형시킬수 있을 것이다.

에너지 기반 모델 v.s. 확률 모델

에너지는 비정규화^unnormalised 된 음수 로그 확률로 볼 수 있고, 정규화 이후 깁스-볼츠만 분포^{Gibbs-Boltzmann distribution}를 사용하여 확률로 변환할 수 있다: \(P(y \mid x) = \frac{\exp (-\beta F(x,y))}{\int_{y'}\exp(-\beta F(x,y'))}\)

$\beta$는 양수^{positive constant}이며 모델을 적합하기 위해 조정되어야 한다. $\beta$ 가 클 수록 모델은 더욱이 변동이 심해지고 $\beta$ 가 작을수록 모델은 매끄러워진다. (물리학에서는, $\beta$ 는 역온도^{inverse temperature}를 뜻한다: $\beta \rightarrow \infty$라는 말은 온도가 0으로 수렴한다는 뜻).

이제 만약 y에 주변화^marginalize 를 하면: $P(y \mid x) = \int_z P(y,z \mid x)$, 다음과 같은 수식을 갖게된다. \(\begin{aligned} P(y \mid x) & = \frac{\int_z \exp(-\beta E(x,y,z))}{\int_y\int_z \exp(-\beta E(x,y,z))} \\ & = \frac{\exp \left [ -\beta \left (-\frac{1}{\beta}\log \int_z \exp(-\beta E(x,y,z))\right ) \right ] }{\int_y \exp\left [ -\beta\left (-\frac{1}{\beta}\log \int_z \exp(-\beta E(x,y,z))\right )\right ]} \\ & = \frac{\exp (-\beta F_{\beta}(x,y))}{\int_y \exp (-\beta F_{\beta} (x,y))} \end{aligned}\) 그러므로, 에너지 함수 $F_\beta$^{자유 에너지 Free Energy}를 재정립함으로써, 잠재변수 모델에서의 잠재변수 $z$를 확률적으로 옳바르게 제거 가능하다.

자유 에너지

\(F_{\beta}(x,y) = - \frac{1}{\beta}\log \int_z \exp (-\beta E(x,y,z))\) 위 수식을 계산하는 것은 굉장히 어렵다… 실제로, 이는 거의 불가능에 가깝다. 만약 모델 안에 최소화하고 싶은 잠재변수를 가졌거나, 주변화를 하고 위 공식의 무한 $\beta$극값에 대해 최소화 하려는 잠재변수를 갖는다면, 계산이 가능하기는 하다.

위 $F_\beta(x, y)$ 정의에서, $P(y \mid x)$ 는 그저 깁스-볼츠만 공식의 적용이고 이 과정에서 $z$는 자연히 주변화 되어진다. 물리학자들은 이를 “자유 에너지” 라고 부르기에, $F$라고 표기된다. 그래서 $e$는 에너지,$F$는 자유 에너지이다.

***문제: 확률-기반 모델 또한 주변화가 가능한 잠재변수를 가질 수 있는데, 에너지-기반 모델이 주는 이점을 서술할 수 있는가?

에너지 기반 모델과 확률 기반 모델의 차이점은, 확률 모델은 최소화할 목적함수^{objective function}를 직접 고를 수 없고, 우리가 다루는 모든 항목들이 정규된 분포여야하는 확률적 구조에 얽매여야 한다는 것이다 (변분 방법^{variational methods} 등으로 근사시킬수 있다). 여기서, 이 모델들을 통해 우리가 하고자 하는 것은 결국 의사결정을 내는 것이다. 자동차를 운전시키는 시스템을 만들었다고 가정하고, 그 시스템이 0.8의 확률로 좌회전을 하라고 하고 0.2의 확률로 우회전을 하라고 한다고 해보자. 확률이 0.2든 0.8이라는 것은 전혀 중요치 않다 – 의사결정을 내려야만 하는 우리가 정말 원하는 것은 가장 최적의 의사결정을 만드는 것이다.

그러므로 의사결정을 내려야하는 상황에서 확률은 전혀 쓸모가 없다. 만약 자동화된 시스템에서 나온 출력값과 다른 출력값을 조합 해야하고 (예를 들어, 사람이나 다른 시스템 등), 그 시스템들이 같이 학습되어지지 않아, 서로 따로 학습되었다면, 좋은 결정을 내기위해서는 두개의 시스템의 점수를 조합한 보정 점수가 필요하다. 점수들을 확률로 바꾸는 것이 점수들을 보정하기 위한 단 하나의 방법이다.

다른 모든 방식들은 비슷하거나 혹은 더 못한 것으로 여겨진다. 하지만 의사결정을 내기 위해 끝과 끝을 이어 시스템을 학습을 시키겠다면, 최고의 의사결정에 최고의 점수를 준다는 가정하에, 어떠한 스코어 함수를 사용해도 무방하다. 에너지-기반 모델은 우리가 어떻게 모델을 다룰지, 어떤식으로 학습을 시킬지, 그리고 또 어떤 목적 함수를 사용할지에 대해 더 많은 선택지를 제공한다. 만약 확률적 모델을 고수한다면, 최대우도법^{maximum likelihood}을 사용해야만 한다 – 관찰된 데이터에서의 확률이 최대가 되도록 모델을 학습시켜야한다. 문제는 이러한 방식들은 우리가 사용하는 모델들이 “옳은” 모델이여야 하는 경우에만 사용이 가능하다는 것이다 – 그리고 모델은 절대로 “옳을” 수 없다. 저명한 통계학자인 [Goerge Box]는 이렇게 말하였다, “모든 모델들은 전부 틀렸다. 하지만 그 중 일부는 쓸만하다” 그러므로 특히 고차원 공간에서나 문서들과 같은 조합 공간에서의 확률 모델들은 전부 근사모델이다. 어느 방면으로든 확률 모델은 전부 틀렸고, 저 틀린 모델들을 정규화 시키려한다면, 문제를 더 틀리게 만드는 것이다. 그래서 정규화를 시키지 않는 것이 더 나은 방법이다.

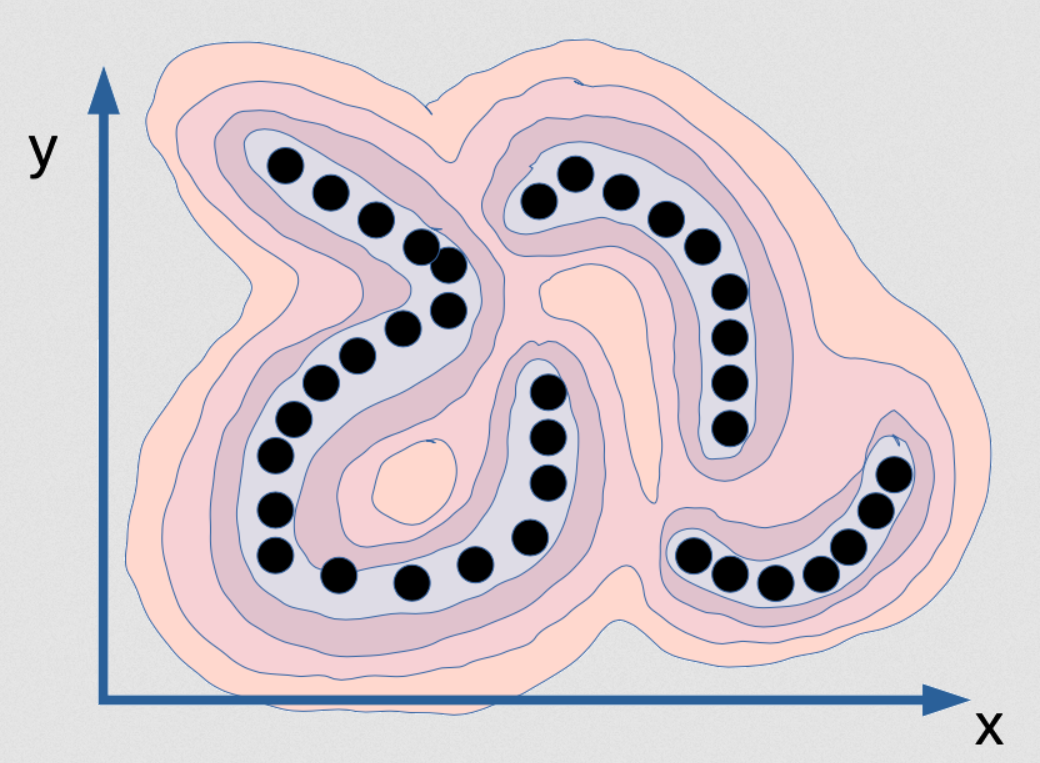
Fig. 2: x 와 y사이의 연관성을 담은 에너지 함수의 시각화

위는 x와 y 간의 의존도를 나타내는 에너지 함수이다. 산맥과 비슷한 형상을 띄고 있으며, 계곡은 검은 점들이 있는 곳이고, 그 주위로는 산들이 즐비해있다. 이제, 위와 같이 확률 모델을 학습시키려 한다고 가정하고, 점들이 무수히 얇은 다양체라고 상상해보자. 그럼 검은 점들의 데이터 분포도는 실제로 그저 한 선으로 되어있으며, 3개의 선이 존재한다. 선들에는 실질적인 넓이가 없으며, 여기에 확률모델을 학습시킨다면 밀도 모델^{density model}은 언제 이 다양체에 있는지 알려줄 것이다.

이 다양체에는 밀도는 무한대이고 $\varepsilon$ 보다 먼 곳들은 전부 0인 모델이 이러한 분포도에는 올바른 모델일 것이다. 밀도가 무한대일 뿐만이 아니라, [x 와 y]의 적분 도한 1이여야 한다. 이는 컴퓨터에 구현시키기 매우 어려운 일이다! 어려운 뿐만이 아니라 기본적으로 거의 불가능에 가깝다. 만약 이 함수를 어떤 종류의 인공 신경망을 통해 계산하려 한다면, 그 인공 신경망은 무한대의 가중치를 가질테고, 또한 모든 정의역에 걸친 출력값의 적분은 1이도록 가중치를 어떻게든 조정을 해야할 것이다. 이건 기본적으로 불가능하다. 이런 특정한 데이터 예를 이용한 정확하고 올바른 확률모델은 불가능하다.

이것은 최대우도법을 위해 필요한 작업이고, 이를 계산 가능한 컴퓨터는 이 세상에 존재하지 않는다. 그렇기에 굳이 신경 쓸 이유는 없다. 이러한 데이터에 딱 맞는 완벽한 밀도 모델을 가지고 있다고 상상해보자. 이는 곧 (x,y) 공간에서의 얇은 판이기에 추론 조차 할 수 없다! 만약 x의 한 값을 주고, “가장 적합한 y값은 얼마인가?”라고 묻는다면, 확률 제로 집합을 제외한 모든 y값은 0의 확률을 갖고 소수의 x값들만 답하는 것이 가능하기 때문에 답을 찾기는 불가능하다. 이러한 x값들은 예로: <!–

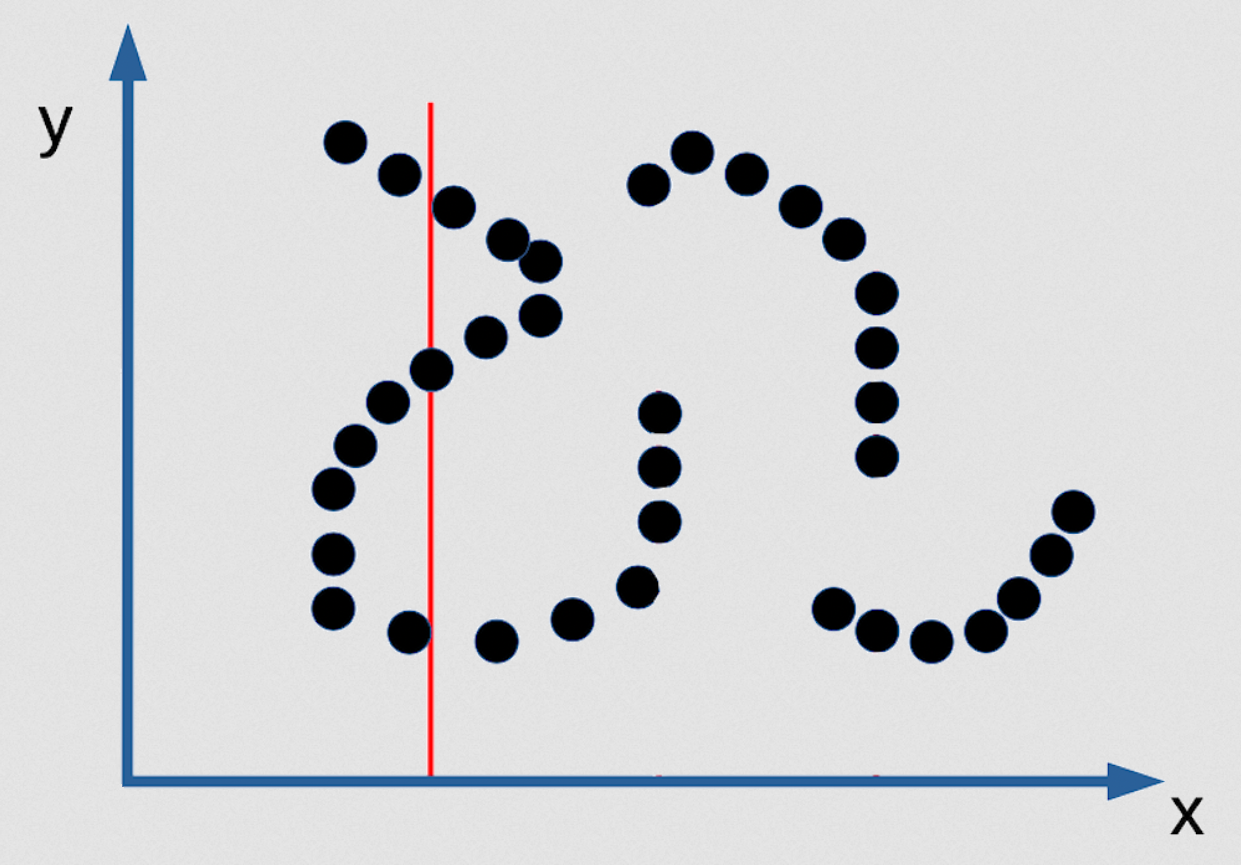
Fig. 3: Example for multiple prediction of EBM as an implicit function

–>

Fig. 3: 예제: 음함수 에너지 기반 모델의 여러 예측값

한 x 값을 기준으로 3개의 y값이 될 수 있으며, 매우 좁기 때문에 찾는 것은 가능치 않다. 이 답을 찾는 추론 알고리즘은 존재하지 않으며, 찾는 단 한 가지의 방도는 대비함수를 매끄럽고 미분가능하게 만들고 하나의 점에서 시작해 기울기 하강법으로 주어진 x 값에서 적절한 y값을 찾는 것이다. 하지만 이것은 데이터 분포도가 위와 같은 특수한 상황이라면 이는 결코 좋은 확률 모델이 될 수 없다. 그러므로 이와 같은 경우는 더 좋은 확률 모델을 만들고자 하는 생각이 오히려 나쁜 결과를 불러온다. 최대우도법은 [이런 경우에서는] 매우 형편없다!

그리고 만약 여러분이 참된 베이즈 학파^Bayesian라면, “아 근데 이건 갖고 있는 밀집함수가 매끄러워야 한다는 사전^prior이 충분히 강하다면 충분히 수정할 수 있어요” 라고 말할 수 있다. 이를 사전이라고 생각 할 수도 있다. 하지만, 베이지안 방식으로 푸는 모든 것이–거기에 로그를 씌우고, 정규화는 생략–결국은 에너지 기반 모델에서 얻을 수 있는 것들이다. (에너지 함수에 추가되는) 규제를 가진 에너지 기반 모델은 가능도가 에너지의 지수인 베이지안 모델과 완전히 똑같으며, $\exp(\text{energy}) \exp(\text{regulariser})$ 는 $\exp(\text{energy} + \text{regulariser})$와 같다. 그리고 지수를 치운다면, 결국 에너지 기반 모델에 규제만 추가된 형식이 된다.

확률 모델과 베이시안 방식 사이에는 유사성이 존재한다, 하지만 최대우도법은 가끔 좋지 않은 결과를 가져오기도 한다. 확률모델이 굉장히 잘못된 고차원 공간에서나 조합공간에서는 더더욱. 이는 이산형 분포에서는 그렇게 크게 잘못된 방식은 아니지만, 연속의 경우 이는 매우 잘못되었다. 그리고 모든 모델은 전부 잘못되었다.