RNN과 LSTM 모델의 구조

개요

RNN은 데이터의 시퀀스^sequence를 다루는 구조의 한 종류이다. 시퀀스란 무엇인가? CNN 수업에서 신호는 도메인에 따라 1차원, 2차원, 3차원도 될 수 있다는 것을 배웠다. 도메인이란 우리가 ‘어디로 부터 매핑을 하였는지’ 와 ‘어디로 매핑을 하는지’에 따라 정의가 내려지며, 도메인은 그저 X에 대한 일시적인 입력이기 때문에, 시퀀스 데이터를 다루는 것은 기본적으로 1차원 데이터를 다루는 것과 동일하다. 그럼에도 불구하고 RNN을 이용해서 두 방향을 가진 2차원 데이터를 다루는 것이 가능하다.

일반^vanilla vs. 순환 ^recurrent 신경망 ^NN

아래는 3개의 레이어를 가진 일반적인 신경망 그림이다(Vanilla라는 단어는 미국식 영단어로 ‘일반적’이라는 뜻을 가진다). 분홍색 방울은 입력값 벡터 x이며, 가운데 은닉층은 초록색으로, 그리고 마지막 파란 레이어는 출력값을 나타낸다. 오른쪽 디지털 전자로 부터의 한 예로, 이것은 현재의 출력값이 오직 현재의 입력값에 의존하는 조합 논리^{combinational logic}와 같다.

Figure 1: 일반적 구조

일반적인 신경망과 다르게, 순환 신경망에서는 현재의 출력은 현재의 입력에만 의존하는게 아니라 위 이미지의 왼쪽과 같이 시스템의 상태 또한 의존한다. 이건 출력이 플립플롭^flip-flop(디지털 전자에서의 기본 메모리 단위)에 또한 의존하는 디지털 전자에서의 순자 논리와 비슷하다. 그러므로, 여기에서 가장 큰 차이점은 일반적인 신경망의 출력은 현재의 입력에만 의존한다는 것이고, RNN의 출력은 시스템의 상태 또한 의존한다는 것이다.

Figure 2: RNN 구조

얀 르쿤 교수의 도표는 한 텐서^tensor에서 다른 텐서로의(하나의 벡터에서 다른 벡터로) 매핑을 표현하고자 뉴런들 사이에 이러한 형태를 더했다. 예를 들어, 위 도표에서의 입력 벡터 x는 위와 같이 새로운 항목들에서 은닉표현^{hidden representation} h로 매핑될 것이다(이 항목들은 회전과 변형의 아핀 변환이다). 그리고 또 하나의 변형을 통해 우리는 은닉 계층에서 마지막 출력으로 가게된다. 비슷하게 RNN 도표에서는 우리는 뉴런들 사이에 같은 추가 항목들을 갖는다.

Figure 3: 얀 르쿤 교수의 RNN 구조

4가지 유형의 RNN 구조와 예시

첫번째 유형은 벡터에서 시퀀스로 이어지는 구조이다 (벡터 → 시퀀스). 입력은 방울 하나이며, 녹색 방울로 표현된 시스템에서 내부 상태에 대한 진화가 이루어진다. 시스템 상태가 진화함에 따라, 매 시간 단계마다 하나의 특정한 출력이 나오게 될 것이다.

Figure 4: 구조 1: 벡터 → 시퀀스

이런 타입의 구조의 한 예는 하나의 이미지를 입력으로 갖고, 입력 이미지를 설명하는 단어의 시퀀스를 출력하는 모델이다. 위 도표에 대해서 설명하자면, 각 파란 방울들은 사전에 있는 영어 단어들의 색인^index을 나타낸다. 예를 들어, 출력 값이 ‘This is a yellow school bus’ 라는 문장이라고 가정해보자. 그렇다면 우리는 처음엔 ‘This’라는 단어의 색인을 갖고, 다음으로는 ‘is’라는 단어의 색인을 갖게 된다. 이런 신경망 결과의 일부는 아래와 같이 나타난다.

예를 들어, 마지막 사진에 대한 설명의 첫번째 열이 “마른 풀밭을 걷고 있는 한 코끼리 무리”와 같이 아주 잘 설명이 되어있는 반면, 두번째 열에서는 실제로 세마리의 강아지가 있지만 “두마리의 개가 풀밭에서 놀고있다”를 출력하고 있다. 마지막 열에서는 더 잘못된 예인, “노란 버스가 주차장에 주차되었다”라고 되어 있다. 일반적으로, 이러한 결과들은 이 신경망이 꽤나 철저하게 망가질 수도 있고, 또 어떤 경우에는 잘 동작할 수 있음을 보여준다.

위와 같은 경우가 바로 이미지를 표현하는 입력 벡터에서 문자나 단어로 이루어진 문장인 시퀀스를 출력하는 신경망의 예이다. 이러한 신경망 구조를 자기회귀 신경망^{autoregressive network}이라고 하며, 자기회귀 신경망은 이전의 출력을 입력으로 피드^feed한 출력을 갖는 신경망이다.

두번째 유형은 시퀀스에서 최종 벡터로 가는 구조이다 (시퀀스 → 벡터). 이 신경망은 심볼들의 시퀀스를 지속적으로 피드하고 끝에서만 최종 출력을 갖는다. 이러한 신경망은 파이썬 코드를 해석하는데 응용될 수도 있다. 예를 들어, 입력으로 다음과 같은 파이썬 프로그램의 코드를 갖는다고 가정해보자.

Figure 5: 구조2: 시퀀스 → 벡터

그렇다면 이 신경망은 위 프로그램의 올바른 답을 출력할 것이다. 다른 예로 다음과 같은 더 어려운 프로그램을 입력으로 갖는다고 한다면

Figure 6: Architecture 2: 시퀀스 → 벡터

12184을 출력할 것이다. 위와 같은 두 예시들은 우리가 이러한 종류의 작업들을 학습시킬 수 있음을 보여준다. 우리는 그저 심볼 시퀀스를 피드하고 최종 출력이 특정값을 갖게하면 된다.

세번째 유형은 시퀀스에서 벡터로 또 그 벡터에서 시퀀스로 이어지는 구조이다 (시퀀스 → 벡터 → 시퀀스). 언어 번역의 대표적인 방법이였던 이 구조는 분홍색인 심볼 시퀀스로 시작하여 하나의 개념을 표현하는 최종 h로 압축된다. 이를테면, 하나의 문장을 입력으로 갖고 임시적으로 표현하려는 뜻과 의미를 나타내는 하나의 벡터로 압축한다. 이후 어떠한 표현을 갖고 있는 축소된 벡터를 받은 신경망이 다른 언어로 다시 펼쳐내는 것이다.

예를 들어, “오늘 나는 매우 행복해” 라는 문장이 이탈리어나 중국어로 번역될 수 있는 것이다. 보통, 이런 신경망은 어떠한 암호화된 문장을 입력으로 갖고, 그것을 압축된 표현으로 변환한다. 최종적으로는, 같은 압축된 형태가 주어졌을 때 이를 해독하게 된다. 최근에는 다음 시간에 다룰 Transformers와 같은 신경망이 언어 번역 작업에서는 이와 같은 신경망보다 더 나은 결과를 내고 있다. 이와 같은 구조는 불과 2 년 전까지만 해도 최첨단^{state of the art}으로 여겨졌다.

Commit suggestion Add suggestion to batch 주성분 분석^PCA을 잠재공간^{latent space}에 적용시켜보면, 아래의 그래프와 같이 의미에 따라 그룹을 이룬다.

Figure 7: 구조 3: 시퀀스 → 벡터 → 시퀀스

확대해보면, 같은 장소에 1월, 11월과 같이, 같은 달을 나타내는 단어가 같은 공간에 군집해 있음을 확인할 수 있다.

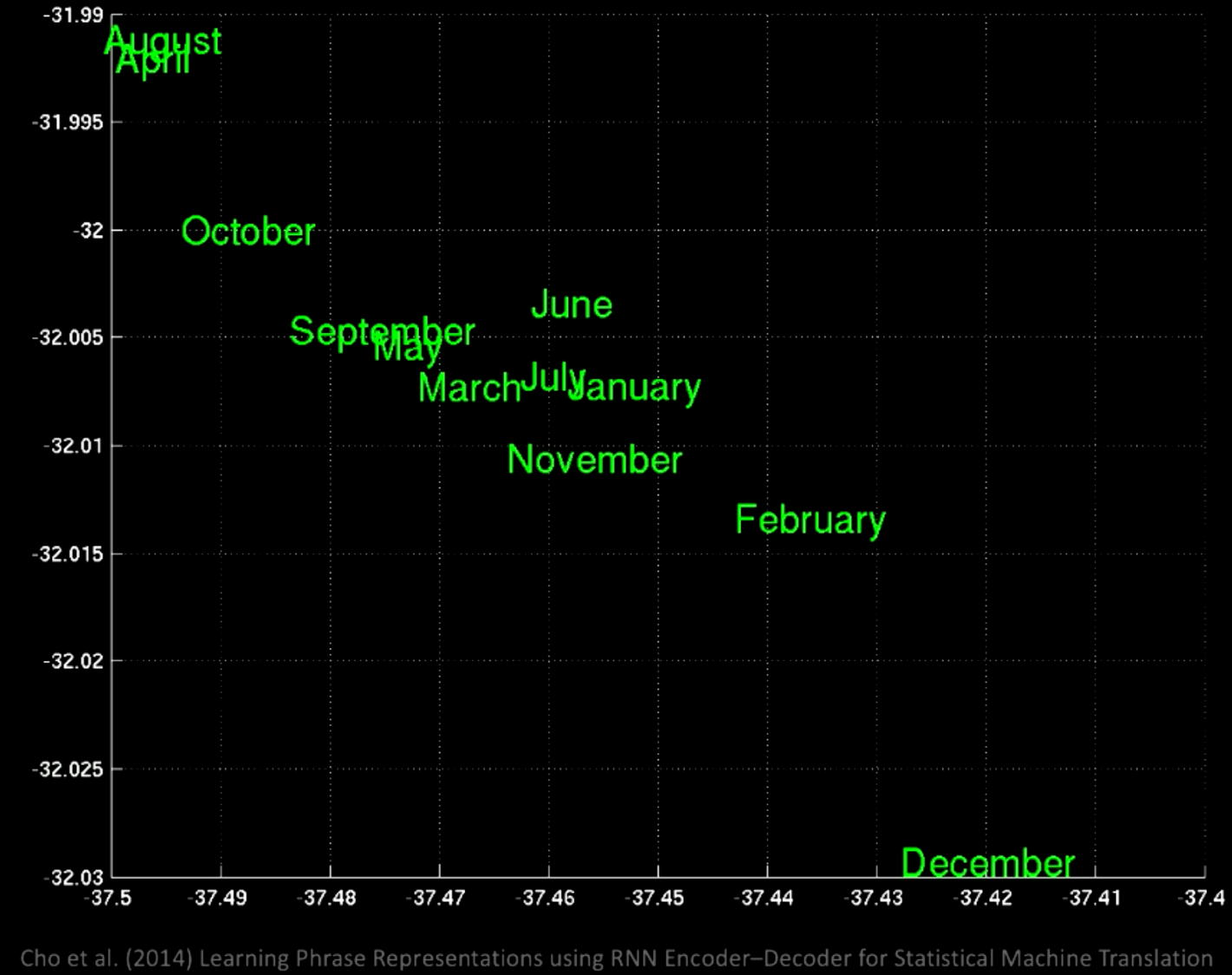
Figure 8: 구조3: 시퀀스 → 벡터 → 시퀀스

다른 부분을 확대해보면, “몇일 전”과 “몇달 전” 등의 구전들을 확인할 수 있다.

Figure 9: 구조 3: 시퀀스 → 벡터 → 시퀀스

이런 예시들에서 우리는 다른 곳에서도 서로 비슷한 의미를 공유하고 있음을 확인할 수 있다.

네번째이자 마지막 유형은 시퀀스에서 시퀀스로 이어지는 구조이다 (시퀀스 → 시퀀스). 이 신경망의 경우, 우리가 입력을 피드를 시작함과 동시에 신경밍은 출력을 갖기 시작한다. 이러한 구조타입의 예로 T9을 들수 있는데, 노키아 핸드폰에서는 (만약 그 시절을 기억하신다면) 문자를 입력함과 동시에 문자 제안의 기능을 가졌다. 다른 예로는 음성을 자막으로 변환하는 기술 또한 있으며, 또 다른 예로 RNN-writer와 같은 텍스트 생성기가 있다. 만약 “토성의 고리가 반짝거릴 때”라고 타이핑하면 텍스트 생성기는 뒤에 내용으로 “두 남자는 서로를 바라보았다” 라는 문장을 제안하는 식이다. 이 신경망은 과학공상소설로 학습되어, 사용자가 무언가를 적으면 그 뒤 내용을 채우는 것에 도움을 준다. 또 다른 하나의 예시는 아래와 같다. 최초의 프롬프트^prompt를 입력하면, 신경망이 나머지를 완성시켜주는 방식이다.

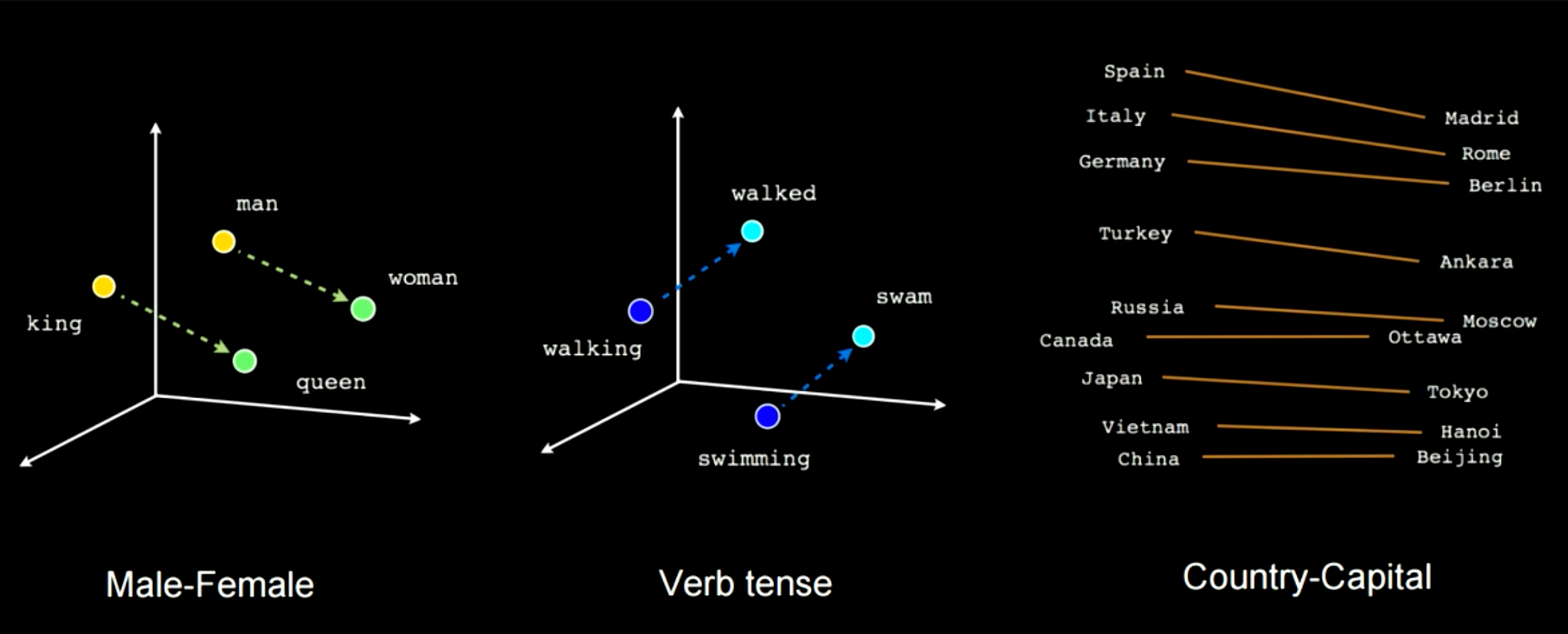
Figure 10: 구조 4: 시퀀스 → 시퀀스

시간에 따른 역전파 ^{Back Propagation through time}

모델 구조

RNN모델을 학습시키기 위해서는, 시간에 따른 역전파^{backpropagation through time (BPTT)}가 반드시 사용되어야 한다. RNN의 모델 구조는 아래와 같이 그려진다. 왼쪽 모형은 루프 ^loop표현을 사용하며 오른쪽 모형은 루프를 풀어 시간에 걸쳐 하나의 줄로 표현된다.

Figure 11: 시간에 따른 역전파

은닉표현^{Hidden representations}은 다음과 같이 표현된다

첫번째 공식은 이전 은닉층^{Hidden layer} 의 배열이 덧붙여져 스택 형태로 되어있는 입력의 회전이 적용된 비선형^non-linear 함수이다. 맨 처음에는 $h[0]$ 는 0으로 설정되고, $W_h$ 는 두 개의 서로 다른 행렬$\left[ W_{hx}\ W_{hh}\right]$로 표현되기에, 가끔씩은 변환^{transformation}이 스택 형태의 입력와 일치하게 다음과 같이 표현된다:

$y[t]$ 는 최종 회전에서 계산되며, 그 후에는 연쇄 법칙를 사용하여 이전 시간 단계에서의 에러를 역전파 연산을 할 수 있다.

언어 모델링에서의 배치화^{Batch-Ification in Language Modeling}

심볼들의 시퀀스를 다룰 때는, 우리는 텍스트를 다른 크기로 배치화시킬 수 있다. 예를 들어, 아래의 도표와 같은 시퀀스를 다룰 때는 시간 도메인이 수직으로 저장된 배치화가 우선 적용되며, 이 경우의 배치 크기는 4로 설정된다.

Figure 12: 배치화

만약 BPTT 주기 $T$가 3이라면, RNN의 첫 입력값 $x[1:T]$와 출력값 $y[1:T]$은 다음과 같다:

RNN을 첫 배치에 실행키려면, 우리는 RNN에 $x[1] = [a\ g\ m\ s]$을 피드시켜야하며, 출력값으로 $y[1] = [b\ h\ n\ t]$를 갖게 해야한다. 은닉표현 $h[1]$은 다음 시간 단계로 보내지며, RNN이 $x[2]$로부터 $y[2]$를 예측하게 도와준다. $h[T-1]$를 마지막 $x[T]$ 과 $y[T]$에 보낸 후, 경사도가 무한으로 전파되지 않도록 $h[T]$와 $h[0]$ 모두의 경사전파과정을 멈추어야한다 (Pytorch에서는 .detach()를 사용하면 된다). 위와 같은 모든 절차는 아래 도표와 같이 표현된다.

Figure 13: 배치화

경사도의 소실과 폭증 ^{Vanishing and Exploding Gradient}

문제점

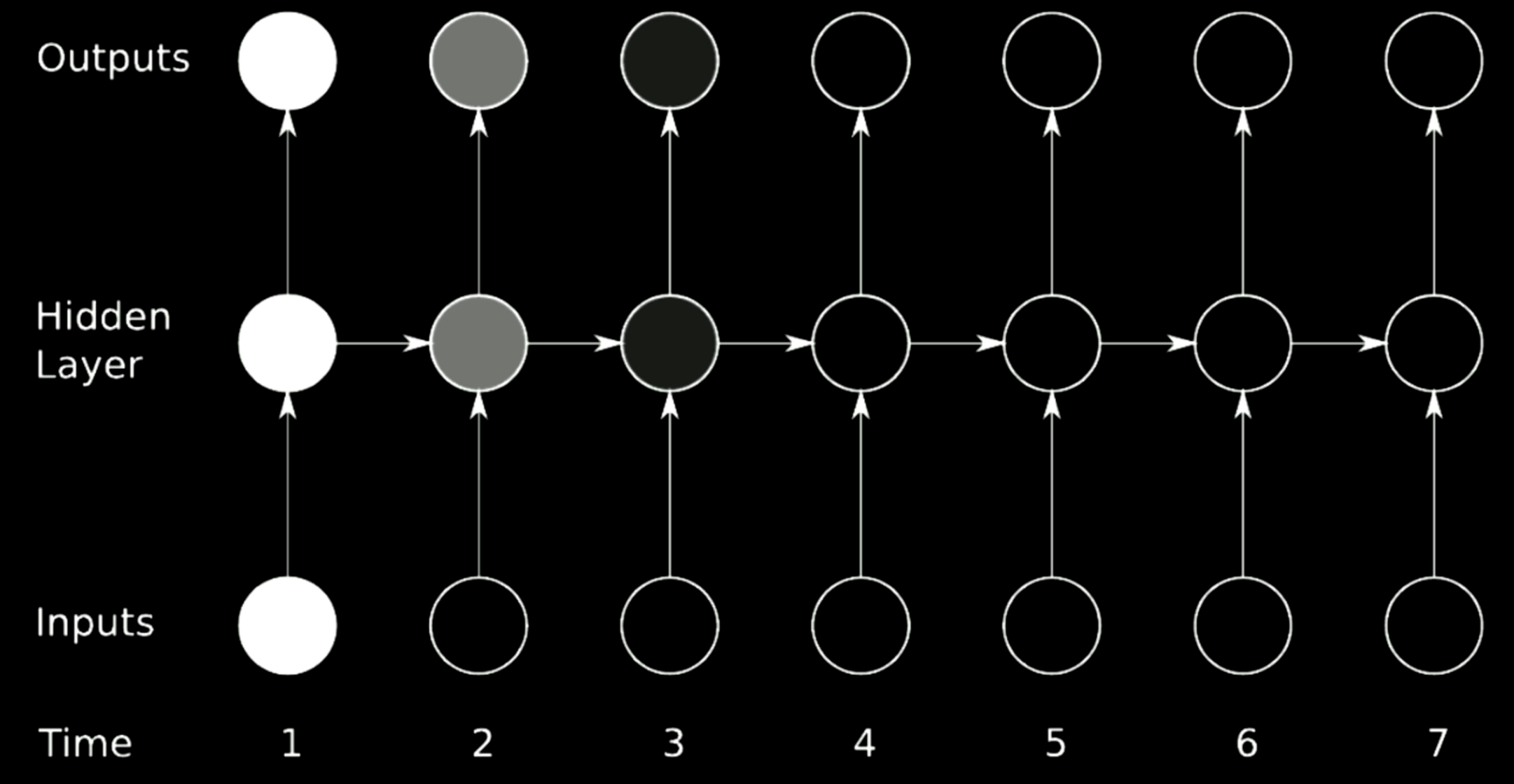
Figure 14: 소실 문제점

위의 도표는 전형적인 RNN 구조이다. RNN에서 이전 단계에 대한 회전을 실행하기 위해서는, 위 모델에서의 오른쪽 방향의 화살표로 표현되는 행렬이 사용된다. 행렬은 출력의 크기를 바꿀 수 있기 때문에, 행렬식^determinant이 1보다 클 경우, 경사도는 시간이 지속될수록 점점 증가하게 되며, 결국엔 경사도의 폭증을 야기한다. 비슷한 맥락으로, 만일 고유치^eigenvalue가 0에 가까울 정도로 작다면, 전파과정에는 경사도가 지속적으로 줄어들게 되며, 결국엔 경사도의 소실을 불러온다.

일반적인 RNN에서 경사도는 받아들일 수 있는 모든 화살표를 통해 전파되어, 경사도를 소신시키거나 폭증시킬 가능성이 높다. 예를 들어 시간 1에서의 경사도가 매우 크다면,(그림에서는 밝은색을 의미한다) 단 한 번의 회전을 통해, 경사도는 매우 크게 줄어들게 되며, 시간 3에서는 결국 사라지게 될 것이다.

해결방안

경사도의 소실과 폭증을 막기 위한 이상적인 방법은 연결을 건너뛰는 것^{skip connection}이다. 이와 같은 과정을 실행하기 위해서, 신경곱^{multiply networks}이 사용된다.

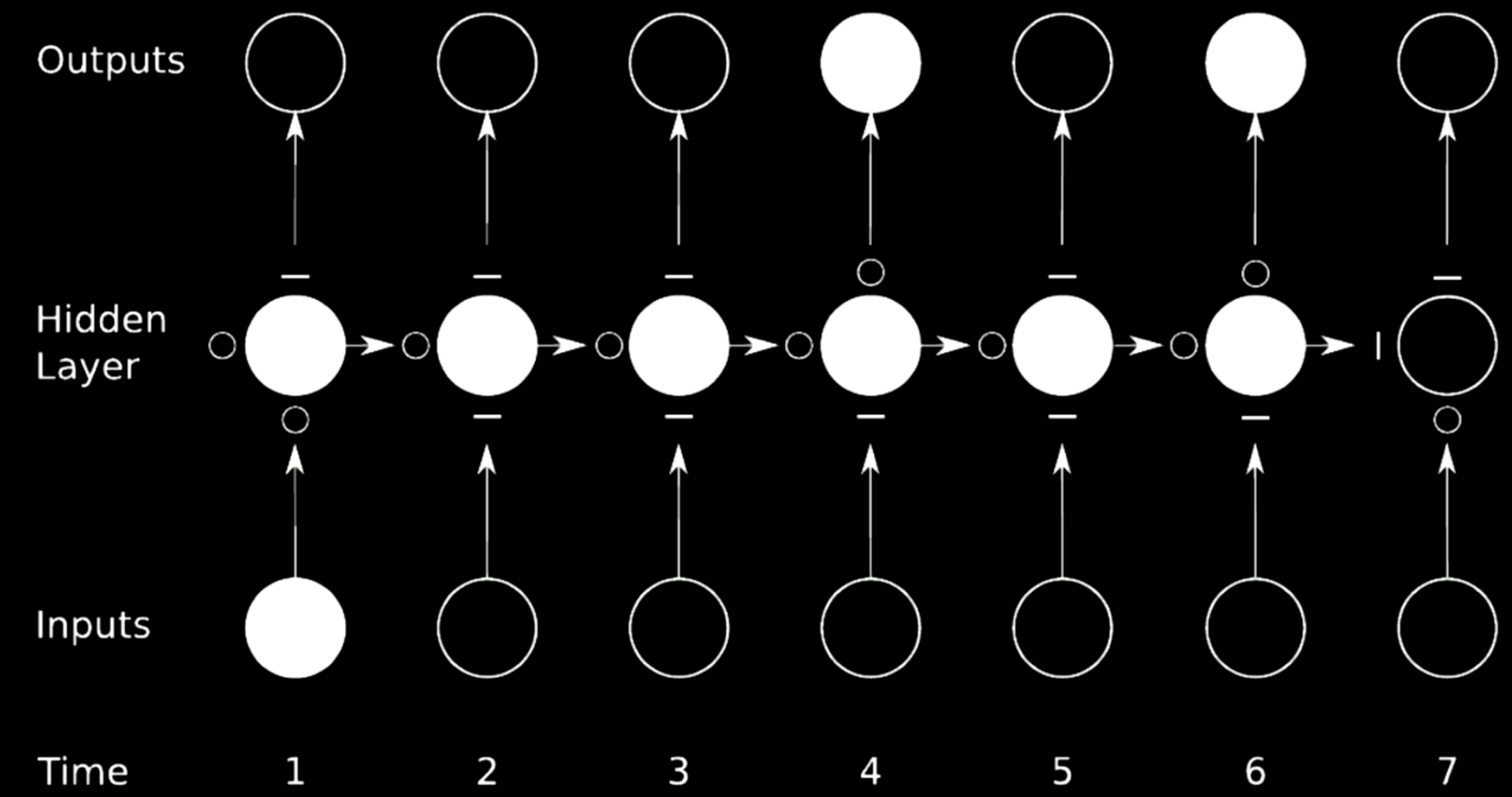
Figure 15: 연결 건너뛰기

위와 같은 경우, 기존의 신경망을 4개 영역으로 나눈다. 첫번째 신경망을 보면, 시간 1에서의 입력값을 갖고 출력값을 은닉망의 처음 중간상태로 보낸다. 이 상태는 경사도를 통과시키는$\circ$와 경사 전파를 막는 $-$로 이루어진 3개의 다른 신경망으로 구성된다. 이러한 기법을 게이트 순환 신경망 ^{gated recurrent network}이라고 한다.

LSTM은 많이 쓰이는 게이트 RNN의 하나로 바로 다음 섹션에서 소개된다.

Long Short-Term Memory

모델 구조

아래는 LSTM을 표현하는 공식이다. 노란색 박스 안에 있는 공식들이 아핀 변환^{affine transformation}이 될 입력 게이트로, 이 입력변환은 후보 게이트인 $c[t]$를 곱함으로 진행된다.

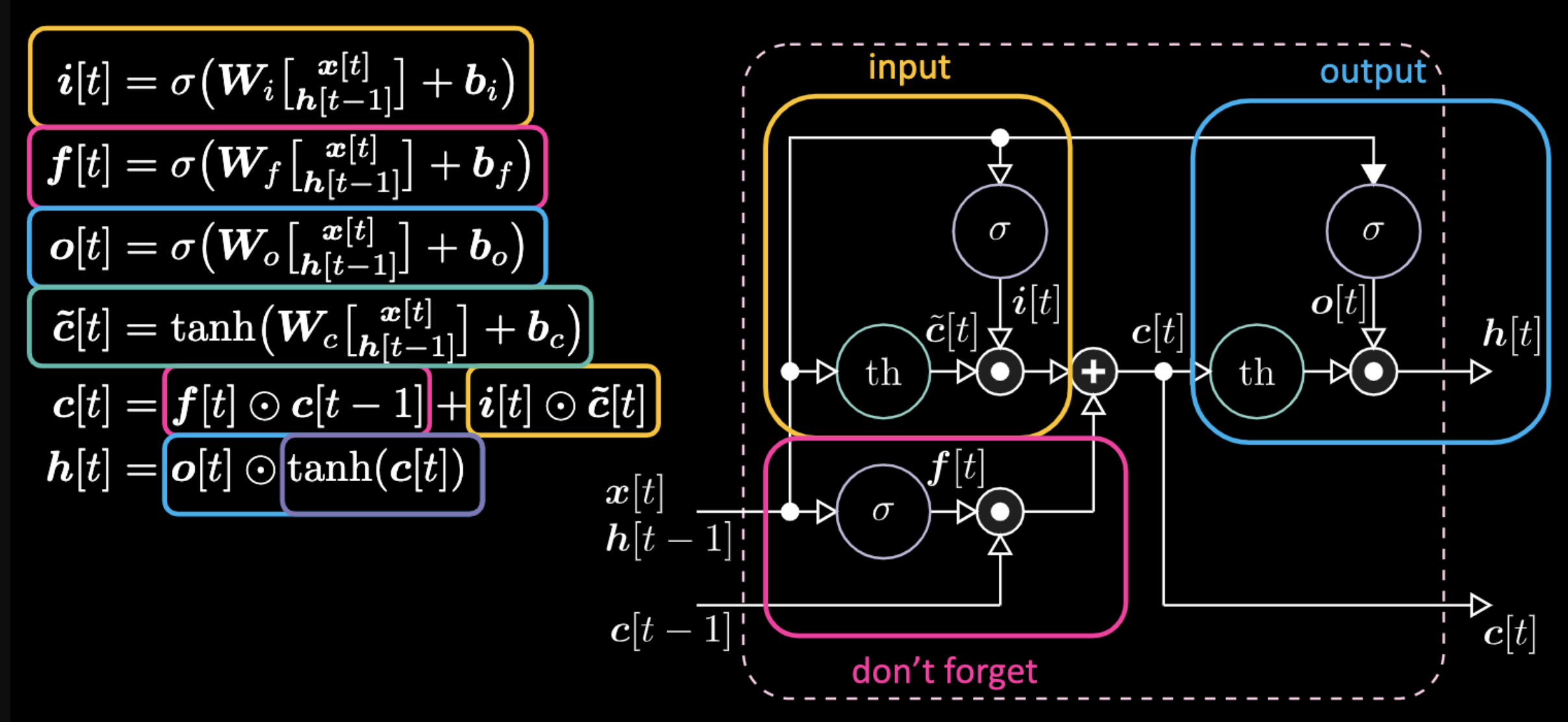
Figure 16: LSTM 구조

돈 포켓 게이트^{don’t forget gate}는 저번 셀 메모리 $c[t-1]$를 곱하고 전체 셀값$c[t]$은 돈 포켓 게이트와 입력 게이트의 합이다. 최종 은닉표현^{hidden representation}은 출력게이트와 유계한^bounded 쌍곡 탄젠트^{hyperbolic tangent} 버전의 세포 $c[t]$의 요소별^elementwise 곱이다. 마지막으로, 후보 게이트 $\tilde{c}[t]$는 간단한 회귀신경망^RNN이기에 우리는 출력을 변조하는$o[t]$, 돈 포켓 게이트 변조를 위한 $f[t]$, 입력 게이트를 변조를 위한 $i[t]$를 갖는다. 모든 메모리와 게이트들간의 상호작용은 전부 곱적용이다. $i[t]$, $f[t]$, $o[t]$ 는 전부 0부터 1까지의 시그모이드^sigmoid이며 0을 곱할시 우리는 닫힌 게이트를 갖는다. 반대로 1을 곱할시, 우리는 열린 게이트를 갖는다.

출력을 막으려면 어떻게 해야할까? 그런 경우에는, 다음과 같이 보라색 내부표현인 $th$를 갖고 출력 게이트에 0에 넣었다고 가정해보자. 그렇다면 출력은 0과 곱해져 0을 갖게되고, 만약 출력 게이트에 1을 넣었다면, 보라색 표현과 같은 값을 갖게된다.

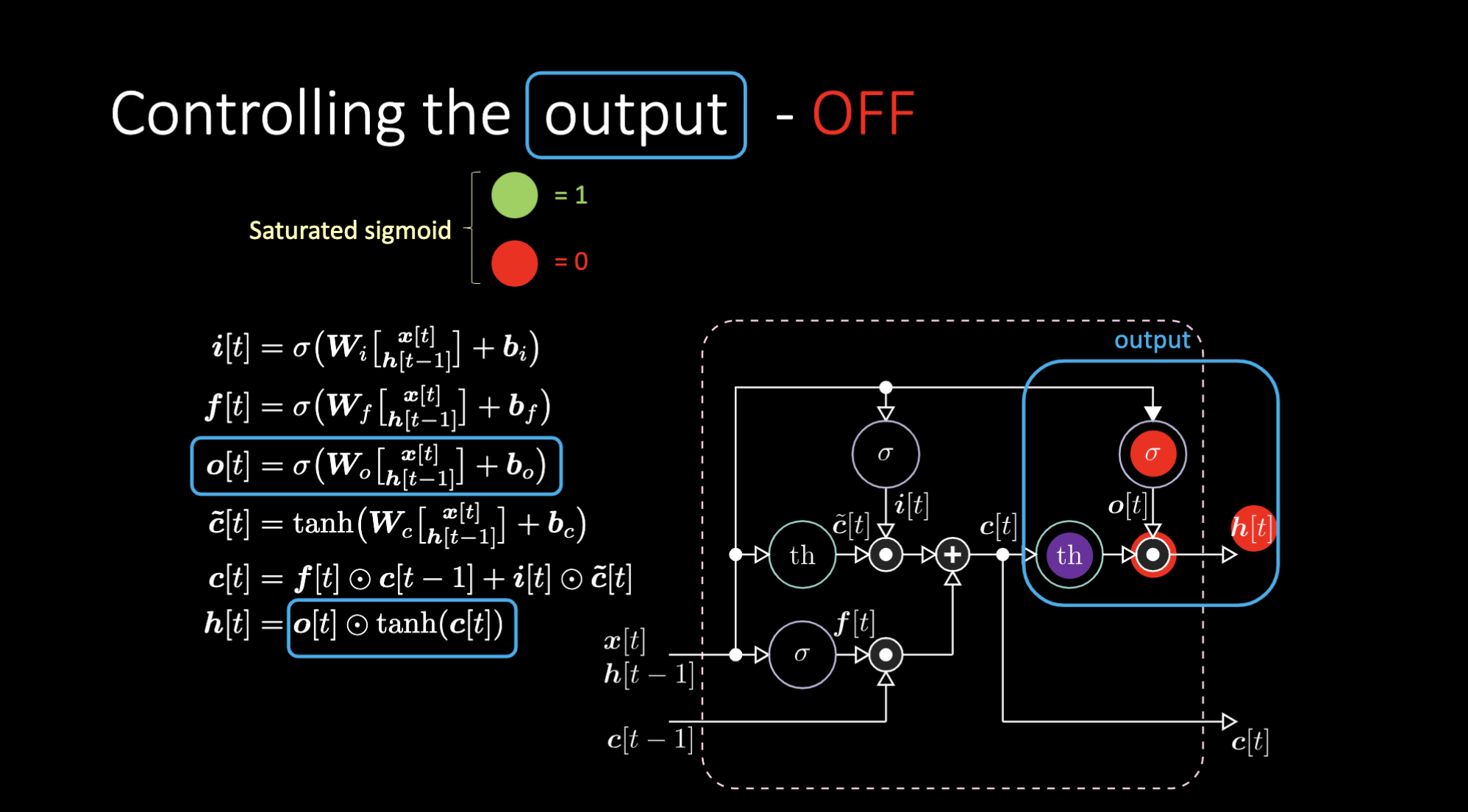
Figure 18: LSTM Architecture - Output Off

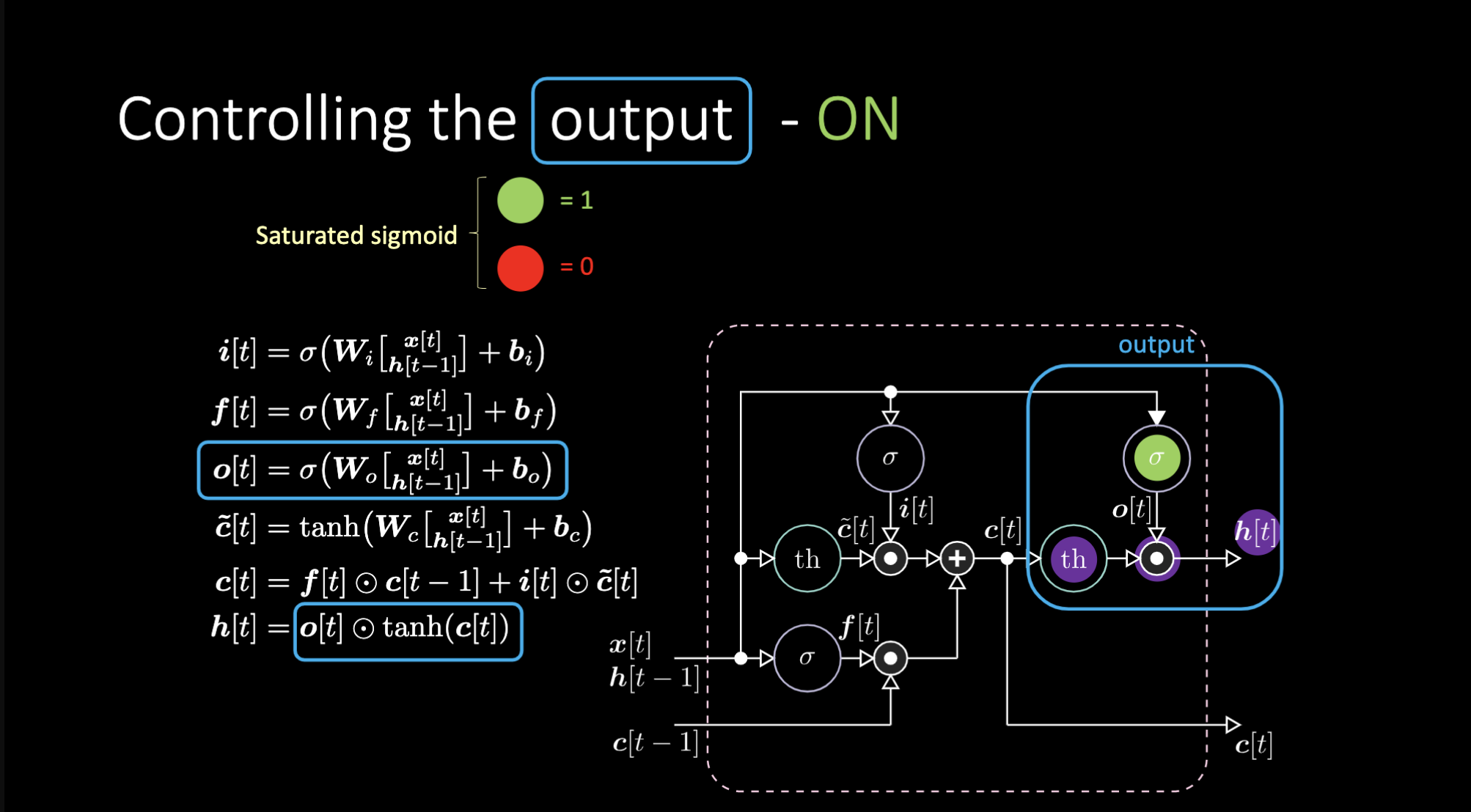
Figure 17: LSTM 구조 - 출력 On

Figure 18: LSTM 구조 - 출력 Off

비슷한 방식으로, 우리는 메모리까지 제어할 수 있다. 예로, $f[t]$ 와 $i[t]$를 0으로 만들어서 메모리를 리셋할 수 있으며, 곱과 합 이후, 메모리는 0만 남게된다. 그 외에는, $f[t]$를 1로 남겨놓고 내부표현 $th$을 0으로 처리하여 메모리를 유지 할 수도 있다. 그러므로 합은 $c[t-1]$를 갖고 밖으로 보냄을 계속한다. 마지막으로, 입력게이트에 1을 갖고, 곱은 보라색을 가지며, 그러고 돈 포켓 게이트에 0을 설정한다면, 정말로 잊게되는 것이다.

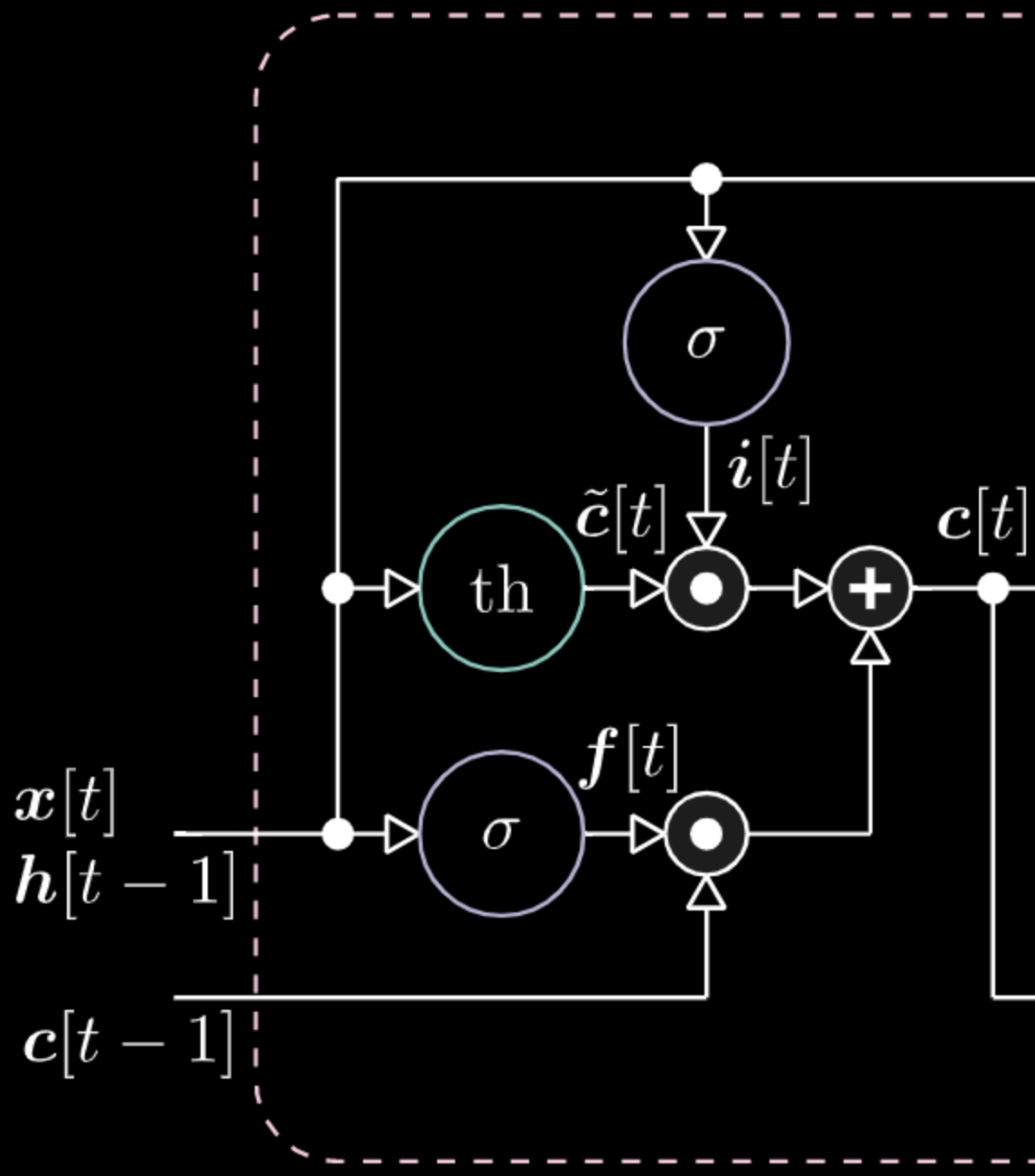
Figure 19: 메모리 셀 시각화

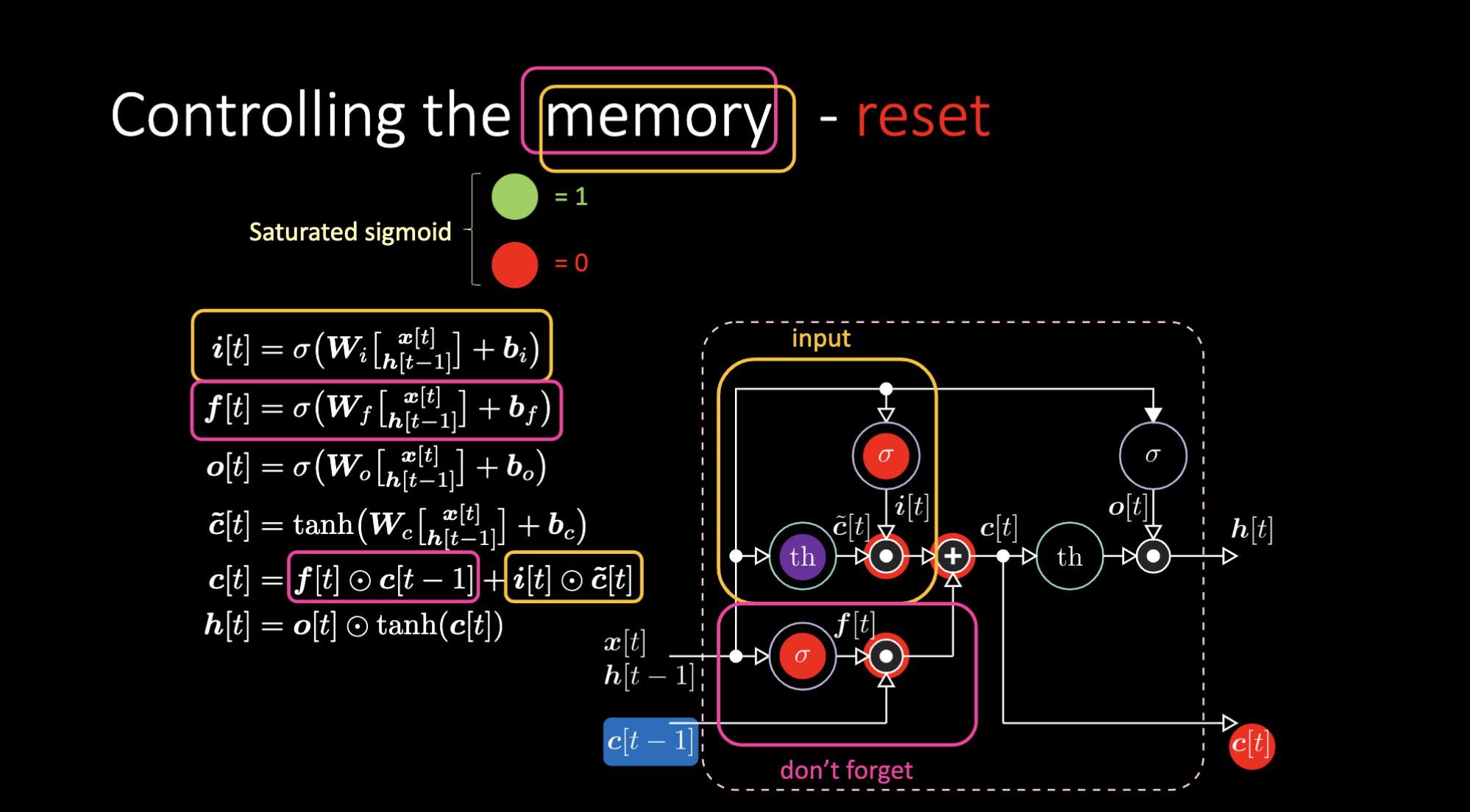
Figure 20: LSTM 구조- 메모리 리셋

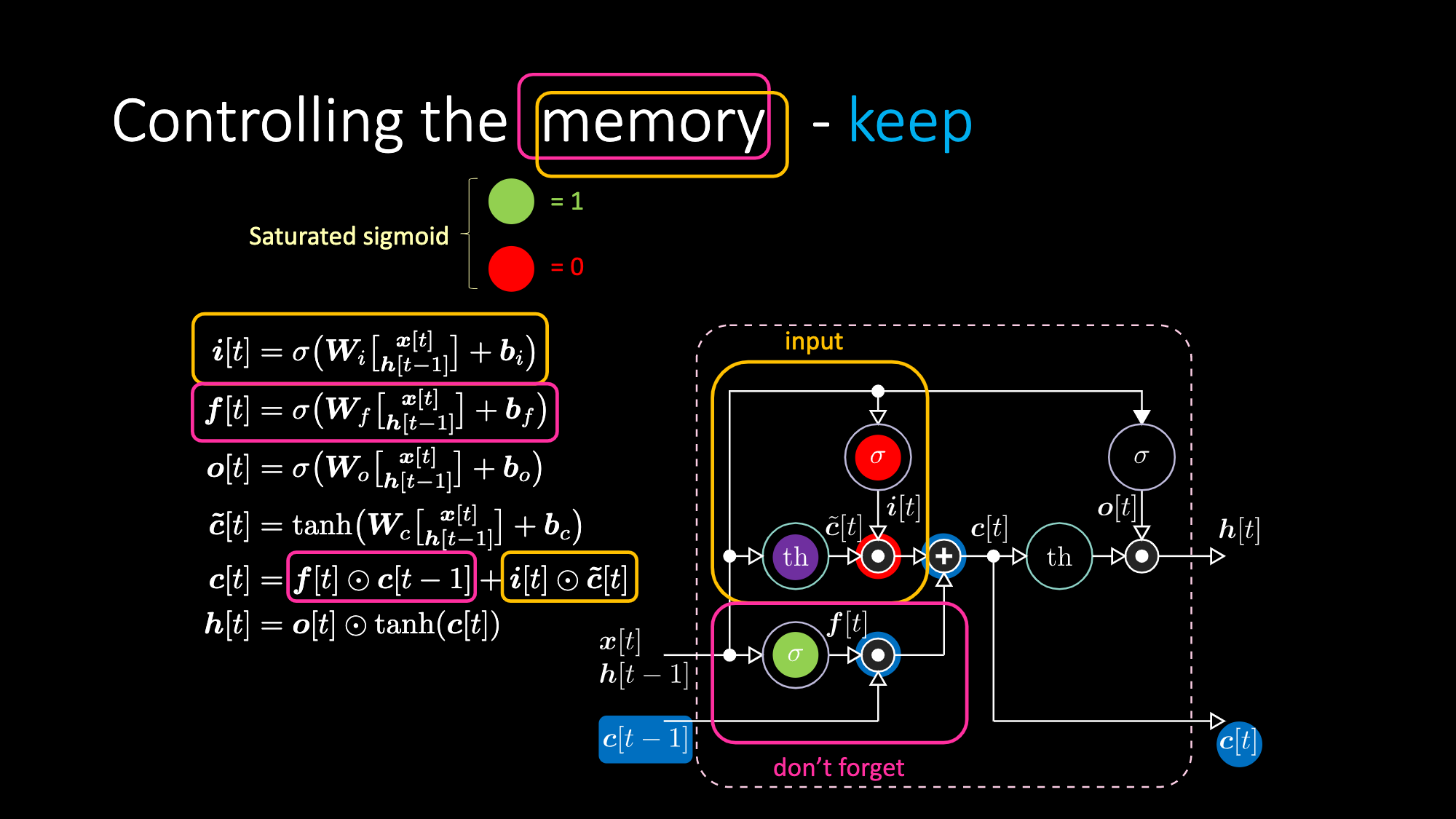
Figure 21:LSTM 구조- 메모리 유지

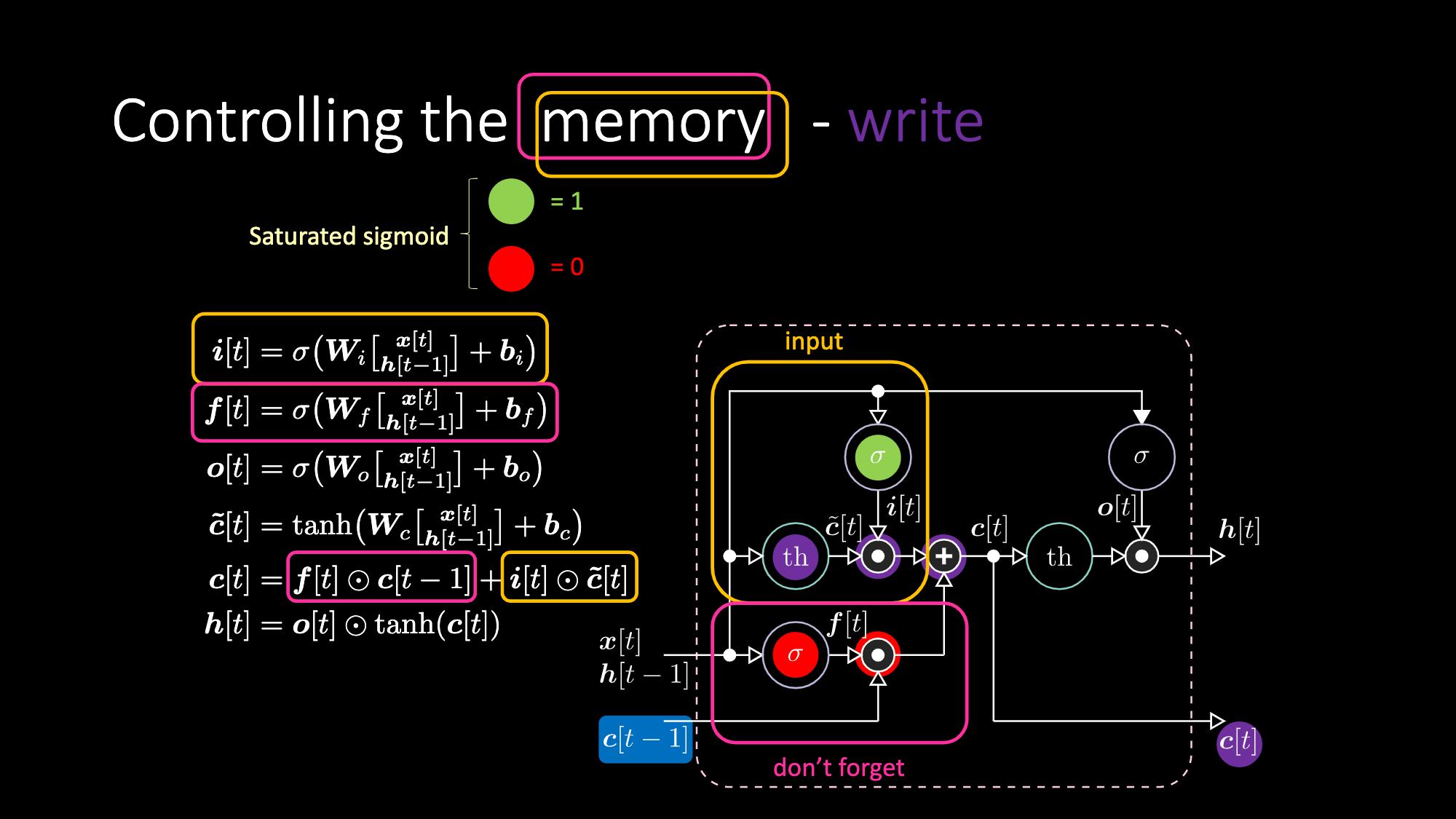
Figure 22: LSTM 구조- 쓰기 메모리

노트북 예제

시퀀스 분류^{Sequence Classification}

시퀀스를 분류하기 위해 요소들과 목표들은 로컬에 표현된다 (단 하나만의 0이 아닌 비트^{non-zero bit}인 입력벡터). 시퀀스는 B로 부터 시작하여, E로 끝나고(“트리거 심볼”이라고 표현한다.), 그 외에는 $t_1$와 $t_2$에 위치한 X 나 Y를 제외하고 {a, b, c, d} 세트 내에서 임의로 선택된다. DifficultyLevel.HARD 의 경우, 시퀀스 길이는 100과 110 사이로 임의의 수로 정해지고, $t_1$은 10에서 20, $t_2$는 50에서 60 사이의 숫자 중 임의로 결정된다. 그 다음으로는 총 4개의 시퀀스인 Q, R, S, U가 존재하는데

1). 데이터셋 탐사

데이터 생성기에서의 리턴 타입은 길이 2의 투플^tuple이며 투플의 첫번째 아이템은 신경망에 피드될 $(32, 9, 8)$의 크기를 가진 시퀀스이다. 각 행에는 8가지의 원-핫 벡터인 심볼들이(X, Y, a, b, c, d, B, E) 존재하며, 시퀀스 행들은 심볼 시퀀스를 표현한다. 모두 0인 첫번째 열은 패딩으로, 패딩은 시퀀스의 길이가 배치의 최장 길이보다 짧을 때 쓰여진다. 튜플의 두번째 아이템은 클래스 라벨 배치로, (Q, R, S, U) 4개의 클래스를 갖기 때문에 $(32, 4)$의 크기를 갖는다. 첫번째 시퀀스는 BbXcXcbE일 경우, 해석된 클래스 라벨은 $[1, 0, 0, 0]$로 Q와 일치한다.

Figure 23: 입력벡터 예시

2). 모델 정의와 학습

심플한 RNN과 LSTM을 만들어 10번의 에폭^epoch동안 학습시켜보자. 학습 루프 동안에는, 다음과 같이 5개의 단계를 꼭 확인해야한다:

• 모델의 전방 전달^{forward pass} 실행
• 손실 계산
• 경사도 캐시 0처리
• 매개변수에 의한 손실 편도함수 계산을 위해 역전파
• 경사도의 반대 방향으로 이동

Figure 24:심플한 RNN vs LSTM - 10 에폭

쉬운 난이도에서는 10 에폭 이후 RNN는 50%의 정확도를 보인 반면, LSTM은 100%의 정확도를 가졌다. 하지만 LSTM은 RNN보다 4배나 많은 수의 가중치를 가졌고, 은닉망도 두 개를 보유하였기 때문에, 같은 조건상에서 비교를 하는 것은 무리가 있다. 100 에폭 후에는, RNN 또한 100%의 정확도를 가졌지만, LSTM을 학습하는 때보다 더 많은 시간이 걸렸다.

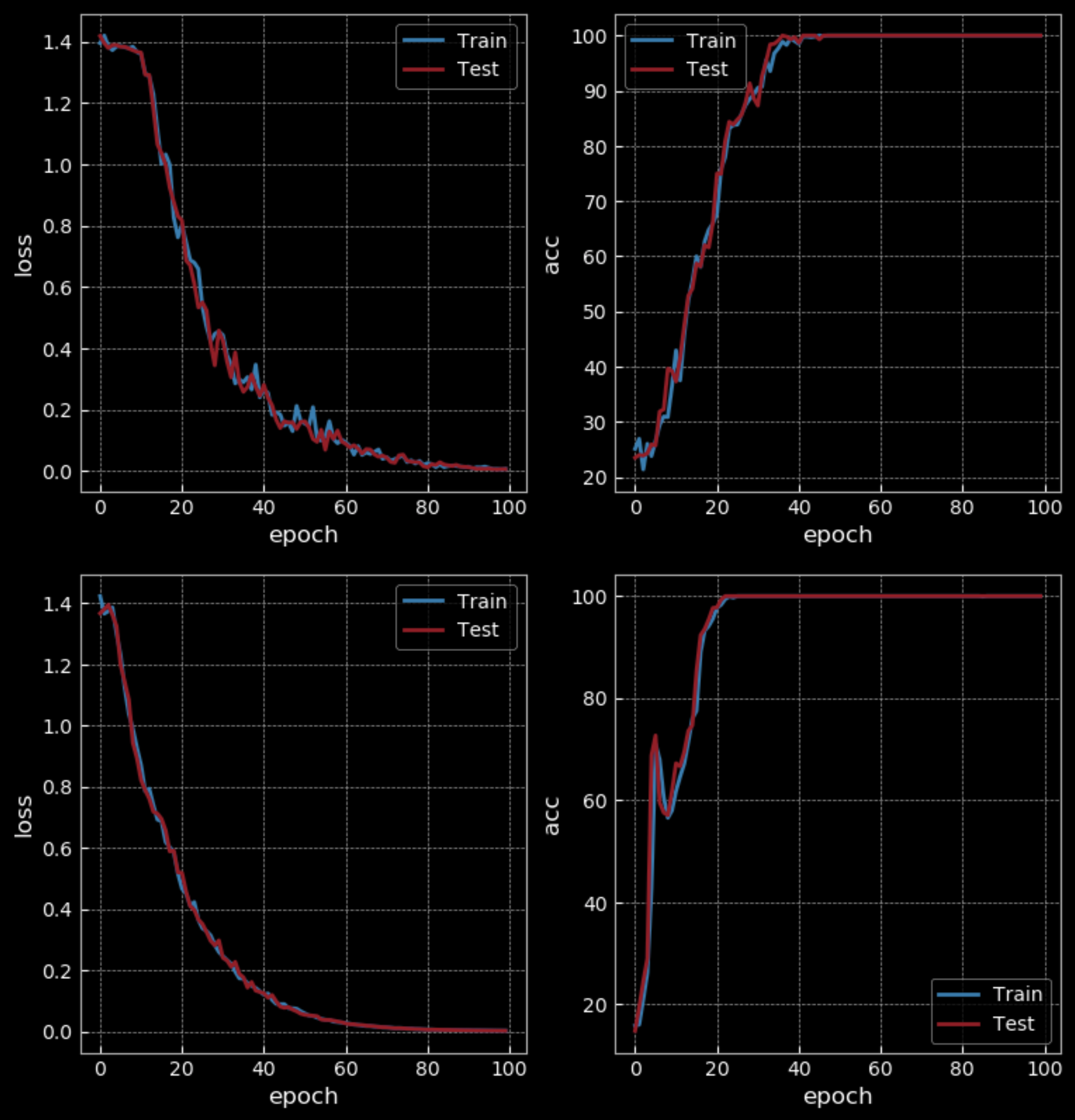
Figure 25:심플한 RNN vs LSTM - 100 에폭

더욱 긴 시퀀스를 사용하여 학습부분에서의 난이도를 증가시키면, RNN은 실패하나 LSTM은 계속 돌아가는 것을 확인할 수 있다.

Figure 26:은닉 상태 값 시각화^{Visualization of Hidden State Value}

위 도표는 LSTM 은닉 상태 값이 시간에 따라 어떻게 바뀌는지 보여준다. 입력값을 쌍곡 탄잰트에 넣어 입력값이 $-2.5$ 이하면 $-1$ 매핑하고 $2.5$ 이상이면 $1$로 매핑한다. 이 경우, 우리는 특정 은닉망이 (그림에서의 5번째 행에서) X를 선택하고, 그 다음 X가 나오기 전까지 값들을 붉은색으로 바꾼다. 그러므로 5번째 셀의 은닉 유닛이 X를 관측 후 촉발되었고, 다른 X를 확인 후 잠잠해졌다. 이런 과정은 시퀀스의 클래스를 인식하는 것을 가능케 한다.

에코 신호^{Signal Echoing}

</sup>

신호를 n번 에코를 주는 것은 동기화된 다대다 작업^{synchronized many-to-many}의 한 예이다. 예를 들어 첫번째 입력 시퀀스가 "1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 ..." 이고 목표 시퀀스가 "0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 ..."라고 해보자. 이런 경우에는 출력은 3번의 시간 단계에 나오기 때문에, 이런 정보를 저장할 단기 메모리가 필요하다. 하지만 언어 모델같은 경우에는 아직까지 말하지 않은 말들을 하게 된다.

시퀀스 전부를 신경망에 보내고 최종 목표를 정하기 전에, 긴 시퀀스를 작은 조각들로 나누어야 한다. 새로운 조각을 피드하는 중에도 은닉 상태를 계속 확인하면서, 다음 새로운 조각이 추가될 때 이를 내부 상태의 입력으로 보내야한다. LSTM에서는 메모리 공간이 충분한 동안에는 메모리의 정보를 오랜시간 보존할 수 있다. 하지만 RNN의 경우, 특정 길이 이상으로는, 과거의 있던 메모리를 잊기 시작한다.