RNNs, GRUs, LSTMs, Attention, Seq2Seq, and Memory Networks

딥러닝 구조들

딥러닝에는 서로 다른 함수들을 구현하기 위한 서로 다른 모듈들이 있다. 딥러닝에서 요하는 전문적 능력 중 하나는 특정한 일을 할 수 있는 딥러닝 구조를 디자인 하는 것이다. 초기에 컴퓨터에 명령을 하기 위해 효율적인 알고리즘으로 프로그래밍을 했던 것과 비슷하게, 딥러닝은 복잡한 함수를 함수 모듈(가능하다면 동적인)로 이루어진 그래프로 단순화 시키고 최종적으로 학습에 의해 함수들을 완성시킨다.

우리가 합성곱 신경망에서 보았듯이, 네트워크 구조는 중요하다.

순환 신경망^{Recurrent Networks}

합성곱 신경망에서는 모듈들로 이루어진 그래프나 모듈의 연결이 순환고리를 가질 수 없다. 그래서 이러한 모듈들에서는 결과를 계산할 때 입력값들이 이미 준비되어 있도록 하는 최소한의 부분적 순서가 있다.

Figure 1 에서 볼 수 있듯이, 순환 신경망에는 순환고리가 있다.

Figure 1. 순환 신경망과 고리

• $x(t)$ : 시간에 따라 달라지는 입력
• $\text{Enc}(x(t))$: 입력의 표현을 생성하는 인코더
• $h(t)$: 입력의 표현
• $w$: 학습 가능한 매개변수들
• $z(t-1)$: 직전 은닉 상태, 즉 직전 시간 단계의 결과물
• $z(t)$: 현재의 은닉 상태
• $g$: 복잡한 신경망일 수도 있는 함수; 입력값 중 하나는 직전 시간 단계의 결과물인 $z(t-1)$
• $\text{Dec}(z(t))$: 결과를 생성하는 디코더

순환 신경망: 순환고리를 펼쳐라

순환고리를 시간에 따라 펼쳐라. 입력은 $x_1, x_2, \cdots, x_T$ 이다.

"
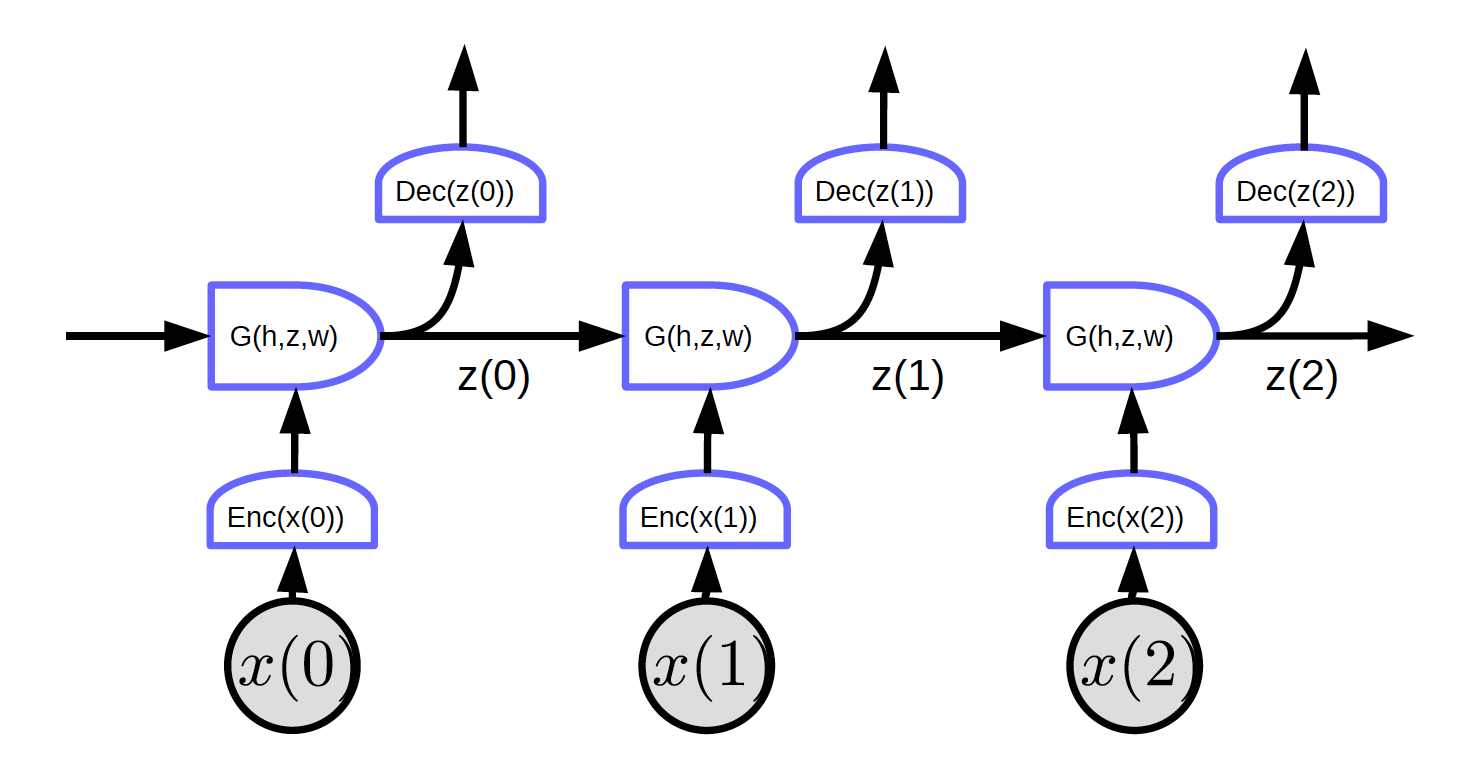
Figure 2. 펼쳐진 순환 신경망

Figure 2 에서 입력은 $x_1, x_2, x_3$ 이다.

t=0일때, 입력값 $x(0)$ 은 인코더로 전해져 입력값의 표현 $h(x(0)) = \text{Enc}(x(0))$ 를 생성한 후 G로 전해져 은닉 상태 $z(0) = G(h_0, z’, w)$ 를 생성한다. $t = 0$일때, $G$에 있는 $z’$은 $0$ 혹은 무작위로 초기화된다. $z(0)$은 디코더로 전해져 결과를 생성하고, 또 다음 시간 단계로 전달된다.

이 망에서는 순환고리가 없기 때문에 경사하강법을 구현할 수 있다.

Figure 2 는 다음과 같은 특징을 가지고 있는 망을 보여준다: 모든 블록이 같은 가중치를 공유한다. 세 개의 인코더, 디코더, 그리고 G 함수는 각각 서로 다른 시간 단계상에서 같은 가중치를 갖는다.

BPTT: 시간상의 역전파^{Backprop through time}. 불행하게도 원시적 RNN 구조상에서는 BPTT가 잘 동작하지 않는다.

RNN들이 가진 문제점들:

1. 경사들의 소멸
   • 긴 순서 상에서는, 가중치 행렬들(의 전치)이 각 시간 단계마다 가중치들에 곱해진다. 만약 가중치 행렬에 작은 값이 들어있으면, 경사들의 놈이 기하급수적으로 작아진다.
2. 경사들의 폭발
   • 만약에 가중치 행렬의 값이 크고 순환 신경망의 비선형 함수값에 제한이 없으면, 경사값들은 폭발할 것이다. 가중치들은 업데이트 단계에서 발산할 것이다. 이를 해결하기 위해서는 매우 작은 학습 속도를 사용해야 할 수도 있다.

순환 신경망을 사용해서 얻을 수 있는 한 가지 장점은 과거의 정보를 기억할 수 있다는 것이다. 그러나 간단한 구조의 RNN은 오래전의 정보를 쉽게 기억하지 못한다.

경사들의 소멸 문제를 가지고 있는 예시:

입력값은 C 언어의 글자들이다. 이 시스템은 입력값이 문법적으로 맞는지 판단한다. 문법적으로 맞는 프로그램은 중괄호와 괄호 숫자가 알맞게 있어야 한다. 그래서 망은 중괄호와 괄호 숫자를 기억하고 이들을 제대로 닫았는지 확인해야 한다. 망은 이러한 정보를 은닉층에 계수기처럼 저장해야 한다. 그러나 경사의 소멸 때문에 긴 프로그램에서는 정보를 유지하기가 어렵다.

RNN 트릭

• 경사값 자르기: (경사값의 폭발 방지) 경사값이 너무 커질 때 값을 작게 하기
• 초기화 (알맞은 초기화로 폭발/소멸을 막을 수 있음)
• Initialization (start in right ballpark avoids exploding/vanishing) 가중치 행렬을 잘 초기화해서 놈을 어느정도는 유지할 수 있다. 예를 들어, 직교 초기화는 가중치 행렬을 랜덤 직교 행렬로 초기화시킨다.

곱셈 모듈

곱셈 모듈은 단순히 입력값의 가중합을 계산하는 것이 아니라, 입력값의 곱을 계산한 후 그것의 가중합을 계산한다.

$x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ 그리고 $z \in {R}^{d\times1}$ 라고 가정해보자. 여기서 U는 텐서이다.

여기서 $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

이 시스템의 결과는 입력값과 가중치들의 일반적인 가중합이다. 여기서 가중치 값들 또한 입력값과 가중치들의 가중합이다. 초월망^Hypernetwork 구조: 가중치들이 다른 네트워크에 의해 계산된다.

어텐션^attention

$x_1$ 과 $x_2$ 는 벡터이고, $w_1$ 와 $w_2$ 는 값이 각각 0 과 1 사이이고, $w_1 + w_2 = 1$ 인 소프트맥스 함수를 거친 스칼라 값들이다.

$w_1x_1 + w_2x_2$ 는 $w_1$ 와 $w_2$를 계수를 가지는 $x_1$ 와 $x_2$ 의 가중합이다.

$w_1$ 과 $w_2$의 상대적인 크기를 바꿈으로서, 우리는$w_1x_1 + w_2x_2$의 결과를 $x_1$ 혹은 $x_2$ 혹은 $x_1$ 과 $x_2$ 의 선형결합으로 나타낼 수 있다.

입력 값은 여러개의 $x$ 벡터를 가질 수 있다($x_1 과 $x_2$ 이외에도). 이 시스템은 다른 변수 z에 의해 결정되는 알맞은 조합을 찾는다. 어텐션 메커니즘은 신경망으로 하여금 특정 입력에 집중하고 나머지를 무시할 수 있도록 한다.

어텐션은 트랜스포머^transformer 구조, 혹은 다른 어텐션들을 사용하는 NLP시스템에서 점점 더 중요해지고 있다. z가 데이터에 대해 독립적이기 때문에 가중치들도 데이터에 대해 독립적이다.

개폐식 순환 신경망^{Gated Recurrent Units} (GRU)

위에서 언급되었듯이, RNN은 경사값의 소멸/폭발 이라는 문제 때문에 상태값들을 오래동안 기억할 수 없다. GRU, Cho, 2014, 는 곱셈 모듈의 활용으로서 이러한 문제를 풀기 위해 고안되었다. 이는 메모리를 가진 순환 신경망의 한 예시이다(다른 하나는 LSTM이다). GRU의 구조는 아래와 같다:

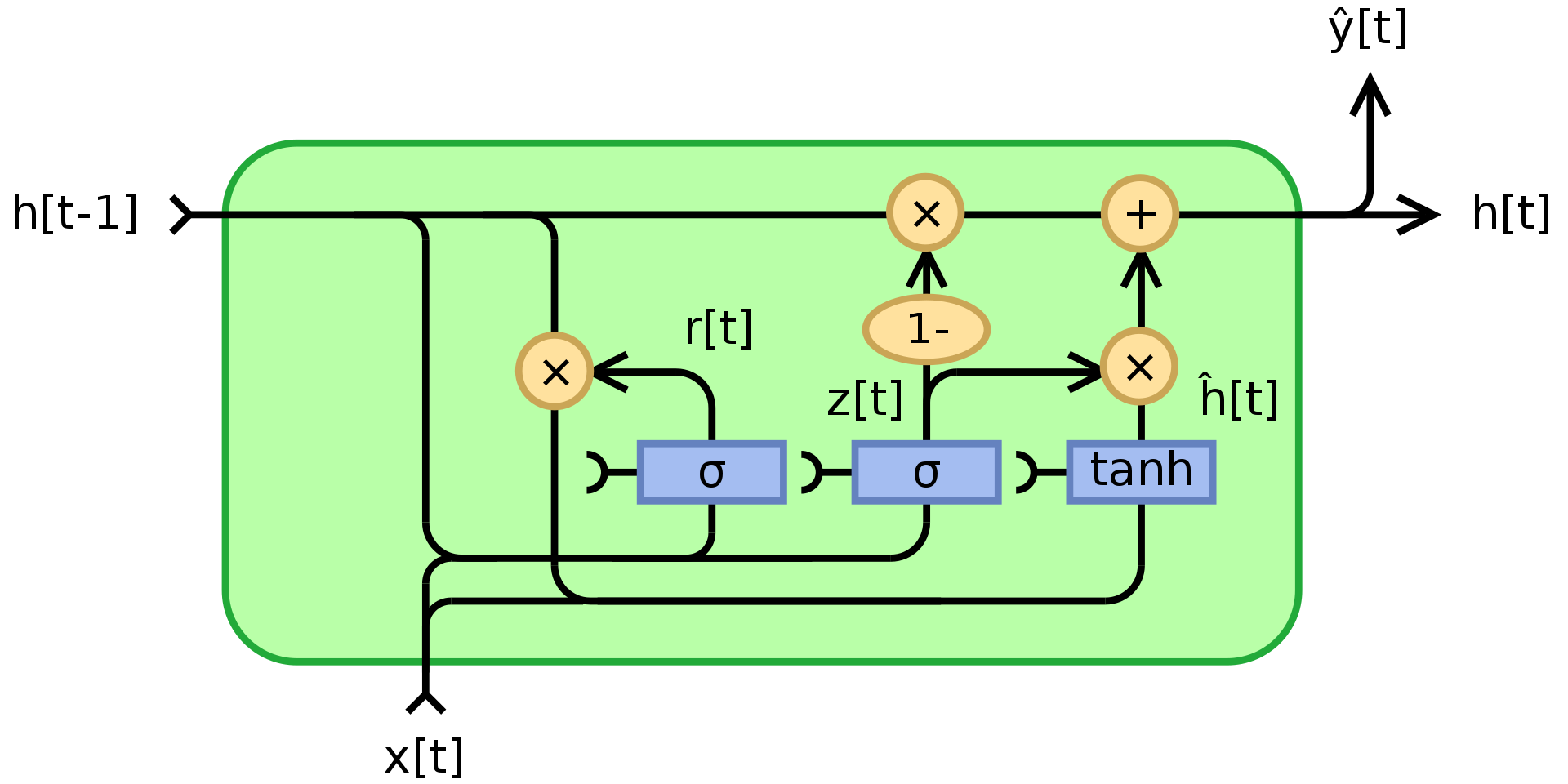
Figure 3. 개폐 순환 신경망

여기서 $\odot$ 는 원소별 곱셈을 뜻하고, $x_t$ 는 입력 벡터 이며, $h_t$ 는 결과 벡터이고, $z_t$ 는 업데이트 게이트 벡터이며, $r_t$ 는 리셋 게이트 벡터이고, $\phi_h$ 는 쌍곡 탄젠트, 그리고 $W$,$U$,$b$ 는 학습 가능한 변수들이다.

구체적으로, $z_t$ 는 문지기 역할을 하는 벡터로서 과거 정보 중 어느정도가 미래로 전달되어야 하는지 결정한다. 이는 입력값 $x_t$ 와 이전 상태 $h_{t-1}$ 에 대한 두개의 선형 결합과 편향에 시그모이드 함수를 적용시킨다. 시그모이 함수를 적용시킨 결과로서, $z_t$는 0 과 1 사이의 계수를 갖는다. 최종 결과 상태값 $h_t$는 $z_t$를 통한 $h_{t-1}$ 와 $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ 의 오목 조합이다. 만약에 계수가 1이면, 현재 유닛의 출력값은 입력값을 무시한 이전 상태값이다. 만약에 1보다 작다면, 입력값으로부터 새로운 정보를 취하게 된다.

리셋 게이트 $r_t$는 과거 정보를 얼마나 잊을지를 결정한다. 만약에 새로운 메모리 정보 $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ 에서 만약 $r_t$의 계수가 0 이면, 과거 정보를 하나도 저장하지 않는다. 만약에 동시에 $z_t$ 가 0 이면, $h_t$가 입력값만 보기 때문에 시스템이 완전히 초기화 된다.

LSTM (Long Short-Term Memory)

GRU는 LSTM보다 예전에 나온 LSTM의 간소화 버전이다. Hochreiter, Schmidhuber, 1997. 과거 정보를 저장하기 위한 메모리 셀들을 만들어서 LSTM또한 긴 시계열에서 정보 손실 문제를 막기 위해 고안되었다. LSTM의 구조는 아래와 같다.

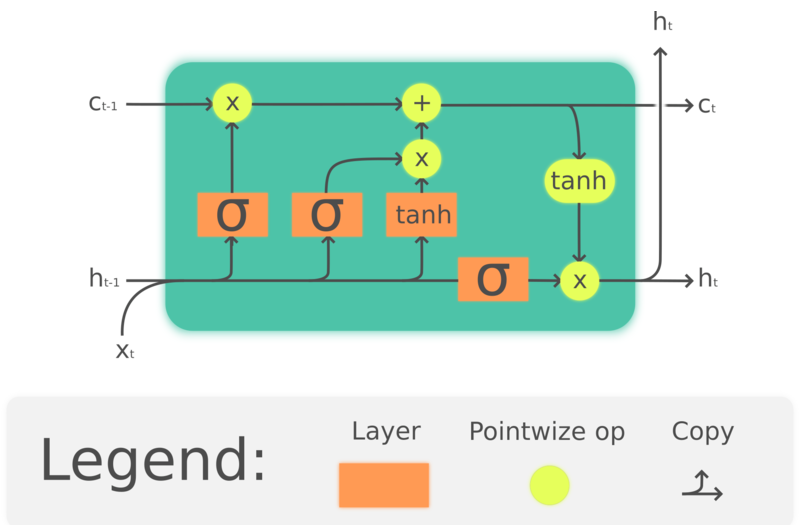
Figure 4. LSTM

여기서 $\odot$ 은 원소별 곱셈이고, $x_t\in\mathbb{R}^a$ 는 LSTM의 입력벡터이고, $f_t\in\mathbb{R}^h$ 는 포겟 게이트의 활성화 함수이고, $i_t\in\mathbb{R}^h$ 는 입력/업데이트 게이트의 활성화 함수이며, $o_t\in\mathbb{R}^h$ 는 아웃풋 게이트의 활성화 함수이고, $h_t\in\mathbb{R}^h$ 는 히든 상태 벡터이며, $c_t\in\mathbb{R}^h$ 는 셀 상태 벡터이다.

LSTM 유닛은 셀 상태 $c_t$를 사용하여 정보를 전달한다. 이는 셀 상태의 정보가 유지되거나 제거될지를 게이트라는 구조를 이용하여 결정한다. 포겟 게이트 $f_t$는 현재의 입력과 이전 상태를 통해 이전 셀 상태인 $c_{t-1}$로부터 어느정도의 정보를 유지할 것인지를 정하고, $c_{t-1}$의 계수로 0과 1사이의 숫자를 출력한다. $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ 는 셀 상태를 업데이트할 새 후보를 계산하고, 포겟 게이트 처럼 입력 게이트 $i_t$는 어느정도의 업데이트가 적용될지 결정한다. 최종적으로, 출력값 $h_t$는 셀 상태 $c_t$에 기초하지만, $\tanh$를 거친 후 출력 게이트 $o_t$의 필터링을 거친다.

LSTM이 NLP에서 널리 사용되고 있지만, 그 유명세가 줄고 있다. 예를 들어, 음성 인식은 템포럴 CNN을 사용하는 추세이고, NLP는 트랜스포머를 사용하는 방향으로 바뀌고 있다.

시퀀스-투-시퀀스^{Sequence to Sequence Model}

이 방식은 Sutskever NIPS 2014에 의해 제안되었고, 기존의 전통적인 방식과 견줄 수 있는 성능을 가진 첫 번째 신경망 번역 시스템이다. 이는 인코더-디코더 구조를 갖는데 여기서 인코더 디코더 모두 다층 LSTM으로 이루어져 있다.

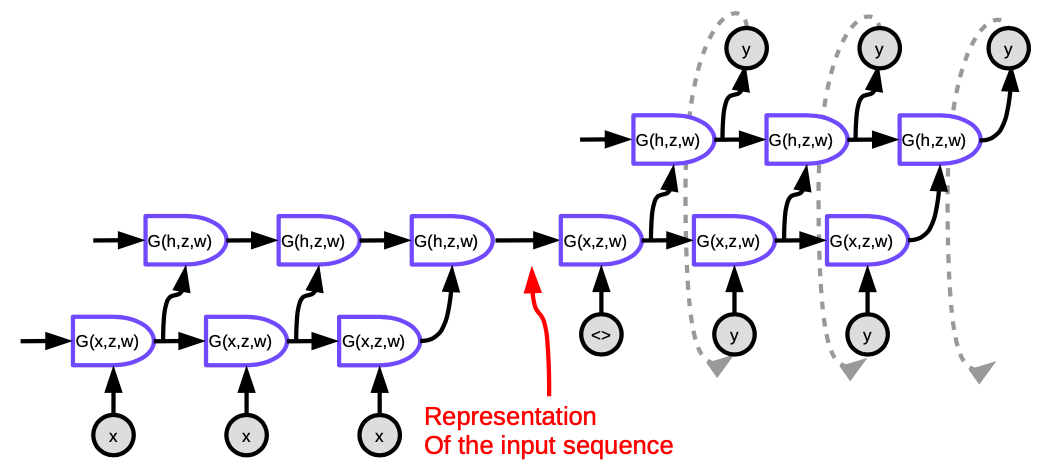
Figure 5. Seq2Seq

그림의 각 셀은 LSTM이다. 왼쪽의 인코더의 경우, 시계열 단계의 수는 번역될 문장의 길이와 같다. 각 단계에는 LSTM이 겹쳐져 있고(논문 상에는 4개) LSTM의 은닉 상태값이 다음 LSTM의 입력값으로 전달된다. 마지막 시간 단계의 마지막 레이어는 문장 전체의 의미를 함축하는 벡터를 출력하고, 이 값이 이제 또다른 다층 LSTM으로 전달되는데(디코더), 이는 타겟 언어에서 단어를 생성해낸다. 디코더에서 단어들은 순서대로 생성된다. 각 스텝은 단어 한개를 생성하고, 이는 다음 스텝의 입력값으로 들어간다.

그러나 이 구조는 두 가지 방면에서 충분치 못하다: 첫째, 문장 전체의 의미가 인코더와 디코더 사이의 은닉 상태값으로 압축되어 들어가야 한다. 둘째로, LSTM은 20단어 이상으로 정보를 저장하지 못한다. 이러한 문제를 해결하기 위해 제시된 것이 Bi-LSTM인데, 이는 LSTM을 쌍방향으로 돌린다. Bi-LSTM에서는 단어가 두 개의 벡터로 인코딩 되는데, 하나는 LSTM을 왼쪽에서 오른쪽으로, 다른 하나는 오른쪽에서 왼쪽으로 돌리며 생성된다. 이는 문장의 길이를 늘려도 정보의 손실을 어느정도 막아줄 수 있다.

Seq2seq 와 어텐션

하지만 위 방식의 성공은 오래가지 못했다. 다른 논문 Bahdanau, Cho, Bengio 은 문장 전체를 하나의 벡터로 압축시키는 것 보다, 각 시간 단계에서 기존의 언어의 같은 의미를 갖는 특정 위치에 시스템을 집중시키는 것(즉, 어텐션 방식)이 더 설득력이 있다고 주장했다.

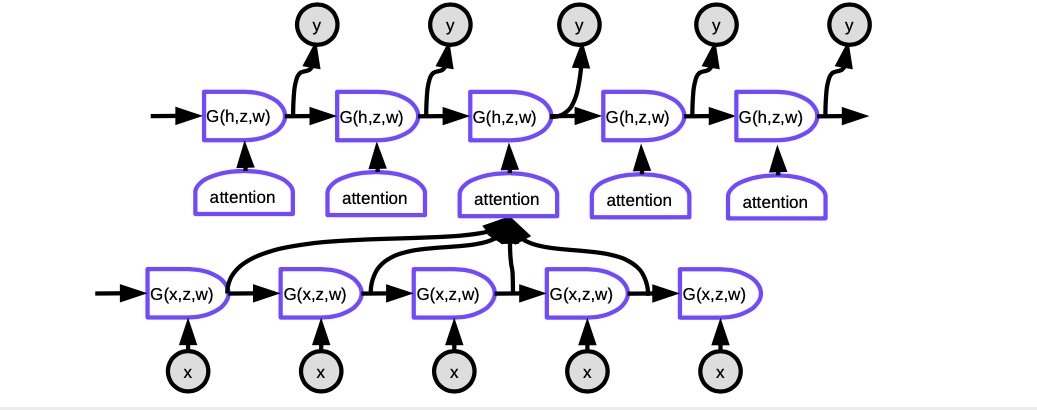
Figure 6. Seq2Seq 과 Attention

어텐션에서 각 시간 단계에서 현재의 단어를 생성하기 위해서 우리는 입력 문장의 어떤 단어의 은닉 표현에 집중할 것인지를 결정할 필요가 있다. 필수적으로, 네트워크는 인코딩된 입력이 현재 디코더의 출력과 얼마나 잘 맞는지를 점수로 평가할 수 있게 된다. 이 점수가 소프트맥스에 의해 정규화 되고, 계수들은 인코더의 서로 다른 시간 단계에서 은닉 상태들의 가중합을 계산하는데 사용된다. 가중치를 조정하며 시스템은 입력값에서 집중할 부분을 찾아낼 수 있다. 여기서 마법은 이러한 계수들을 역전파 방식으로 알아낼 수 있다는 점이다. 이를 직접 만들 필요가 없는 것이다!

어텐션 방식은 신경망 번역 방식을 완전히 바꿨다. 나중에 구글은 Attention Is All You Need이란 논문을 출판했고, 그들은 모든 계층의 뉴런들이 어텐션으로 이루어진 트랜스포머를 사용했다.

메모리 네트워크

메모리 네트워크는 페이스북의 2014 년 연구 Antoine Bordes 와 2015년의 Sainbayar Sukhbaatar 에서 부터 시작되었다.

메모리 네트워크는 뇌 속에 두 가지 중요한 부분이 있다는 아이디어로부터 시작되었다: 하나는 대뇌피질인데, 이 부분에 장기 기억이 저장된다. 다른 하나는 독립된 뉴런들이 모인 해마체로서, 대뇌 피질의 여러 부분으로 전선을 보낸다. 해마체는 단기 기억들을 저장하는 곳으로 알려져 있다. 가장 유망한 이론은, 해마체의 용량이 제한되어 있기 때문에 수면을 취할 때 해마체로부터 대뇌 피질로 정보가 이동한다는 것이다.

메모리 네트워크에는 입력값 $x$ (메모리의 주소라고 생각할 수 있다) 가 있고, 이 입력값을 $k_1, k_2, k_3, \cdots$ (“키”) 와 내적을 통해 비교한다. 이후에 소프트맥스 함수에 넣어, 합이 1이 되는 숫자들의 어레이를 얻는다. 그리고 또 벡터 $v_1, v_2, v_3, \cdots$ 가 있다 (“값”). 이 벡터를 소프트맥스에서 나온 스칼라로 곱한 후 더해 결과를 얻는다(어텐션과 비슷한 방식이다)

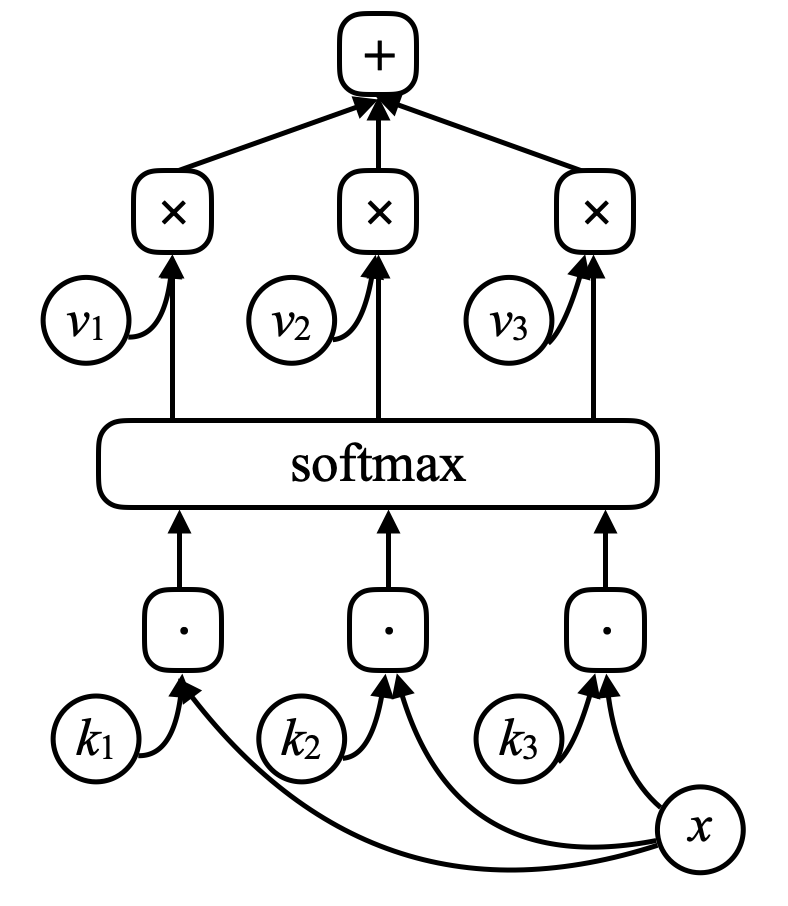
Figure 7. 메모리 네트워크

만약 키들 중 하나(예를 들어 $k_i$)와 $x$가 완벽하게 매치된다면, 이 키와 연관된 계수는 1에 가까울 것이다. 그래서 이 시스템의 출력값은 $v_i$일 것이다.

이는 주소화 연관 메모리이다. 연관 메모리는 만약 입력값이 키와 매치된다면, 그 값이 출력된다. 이는 역전파를 통해 벡터들을 수정할 수 있는 유사하고 미분 가능할 버전일 뿐이다.

저자들은 문장들을 시스템에 순서대로 주며 시스템에 이야기를 해주었다. 문장들은 프리트레이닝이 되지 않은 신경망에 넣어져서 인코딩이 되었다. 문장들은 이런 종류의 메모리에 반환된다. 시스템에 질문을 할때는, 질문을 인코딩하고 신경망의 입력값으로 넣어, 신경망이 메모리에 $x$를 생성하고, 메모리가 값을 반환하는 형식이다.

이 값은, 네트워크의 전 상태값과 함께 메모리에 재접속 할때 사용된다. 그리고 네트워크 전체를 너의 문제에 대한 답을 하도록 학습시킨다. 광범위한 학습 후 이 모델은 실제로 이야기와 답을 저장하도록 학습한다.

메모리 네트워크에서는 입력 값을 받아 메모리의 주소를 출력하는 신경망이 있고, 이를 이용해 값을 네트워크로 가져온 후, 최종적으로 결과를 출력한다. 이는 CPU와 외부 메모리에 읽고 쓰는 컴퓨터와 매우 흡사하다.

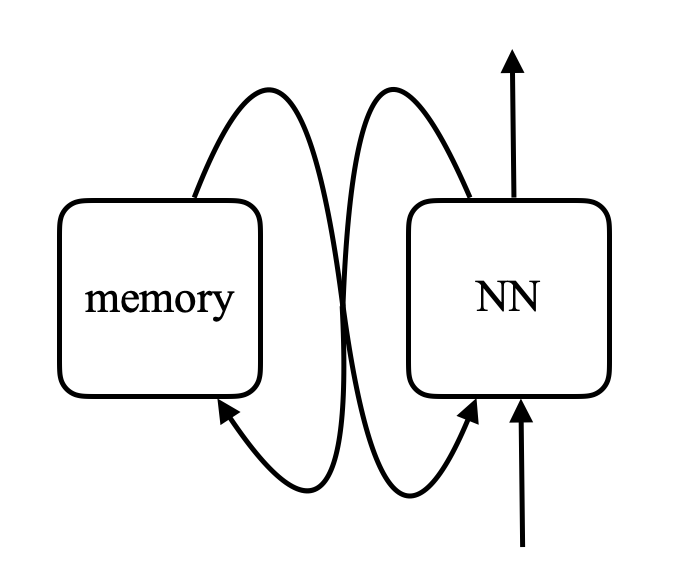
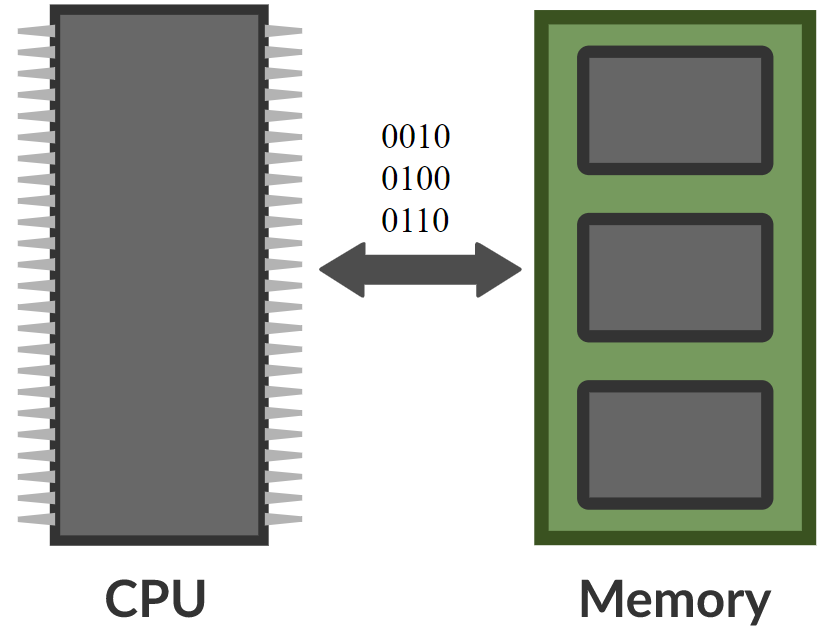
Figure 8. 메모리 네트워크와 컴퓨터의 비교 (사진 출처 Khan Acadamy)

이를 가지고 실제로 미분 가능한 컴퓨터를 만들 수 있다고 상상하는 사람들이 있다. 하나의 예시는, 딥마인드의 Neural Turing Machine 인데, 페이스북의 논문이 arXiv에 출판된 후 삼일 후에 공개되었다.

핵심 아이디어는 입력값을 키와 비교한 후, 계수를 생성하고, 값을 출력하는 것이다. 그게 사실상 트랜스포머의 전부이다. 트랜스포머는 사실상 모든 계층이 이러한 네트워크로 구성된 신경망이다.