합성곱 신경망의 응용

우편번호 인식

이전의 강의에서, 우리는 합성곱 신경망이 숫자를 인식할 수 있다는 것을 확인했지만, 합성곱 신경망이 과연 어떻게 각 숫자를 선택하고 주변 숫자에 의한 인식 교란을 막는지에 대한 의문이 남는다. 다음 단계는 겹치지 않는 개체를 감지하고 NMS^{Non-Maximum Suppression} 알고리즘의 일반적인 접근 방식을 사용하는 것이다. 이제, 입력 데이터가 겹치지 않는 일련의 숫자라고 가정하면, 이를 인식해 내는 전략은 다수의 합성곱 신경망을 학습시키고 이들의 출력값들에 대한 과반수 투표^{majority vote}를 진행하거나, 혹은 합성곱 신경망이 내놓는 최고 점수에 따라 숫자를 선택하는 것이다.

CNN을 이용한 인식

여기서 우리는 겹치지 않는 5자리의 우편번호 인식 과제에 대해 살펴본다. 시스템은 각 숫자를 어떻게 판별해 낼 것인지에 대한 어떠한 지시를 받지 않았으나, 5개의 숫자를 예측해야 한다는 것은 알고 있다. 시스템 (그림 1)은 각각 하나의 출력 내놓는 4개의 서로 다른 크기로 구성된 합성곱 신경망으로 이루어져 있다. 출력은 행렬으로 표현된다. 네 개의 출력은 합성곱 신경망의 마지막 레이어에서 서로 다른 커널 너비를 가진 모델에서 나온 것이다. 각 출력은 10개의 행을 가지는데, 이는 10 종류, 즉 0부터 9까지의 숫자 범주를 나타낸다. 흰색 사각형의 크기가 클수록 해당 범주에서 더 높은 점수를 나타낸다. 이 4개의 출력 블록에서 마지막 커널 레이어의 가로 크기는 각각 5, 4, 3, 그리고 2 이다. 이 커널의 크기는 모델이 입력을 읽어내는 창^window 크기를 결정하고, 따라서 각 모델은 서로 다른 창 크기에 따라 숫자를 예측한다. 이 다음 모델은 과반수 투표를 하고 해당 창에서 가장 높은 점수를 얻은 숫자 범주를 선택한다. 유용한 정보를 추출하기 위해서, 모든 문자 조합이 가능한 것은 아니란 점을 명심해야 하고, 따라서 입력 제한을 활용하는 오류 수정은 모델의 출력이 실제 우편변호가 되도록하는데 유용하다.

그림 1: 우편번호 인식을 위한 여러 분류기

이제 문자열의 순서를 부여하기 위해 우리가 사용할 트릭은 최단 경로 알고리즘이다. 가능한 문자의 범위와 예측할 총 숫자 갯수가 주어졌으므로, 우리는 이 문제를 숫자의 생성 및 숫자 간 전환의 최소 비용 측면에서 접근할 수 있다. 경로는 그래프의 왼쪽 하단 셀^cell에서 오른쪽 상단 셀까지 연속적이어야하고, 경로 구성은 오른쪽에서 왼쪽으로, 그리고 아래에서 위로 이동하는 것으로만 제한한다. 여기서 알아둬야 할 점은, 만일 동일한 숫자가 바로 옆에서 반복된다면, 알고리즘은 단일한 숫자만 예측하는 것 대신 숫자가 반복되고 있음을 구분해 낼 수 있어야 한다.

얼굴 인식

합성곱 신경망은 탐지/인식^detection 작업에서 높은 성과를 보이며, 이는 얼굴 인식^{face detection} 분야에서도 예외는 아니다. 얼굴 인식을 수행하기 위해서 우리는 얼굴이 있는 이미지와 얼굴이 없는 이미지를 모아서 데이터셋을 만들고, 30 $\times$ 30 픽셀 윈도우^window 등의 크기를 가진 합성곱 신경망을 학습시켜 여기에 얼굴이 있는지 없는지를 가려내게 한다. 일단 훈련이 되면, 우리는 이 모델을 새로운 이미지에 적용해보고 대략 30 $\times$ 30 픽셀 윈도우 창 내에 들어오는 얼굴이 있을시, 합성곱 신경망은 해당 위치의 출력을 밝게 표시할 것이다. 하지만 여기에는 두 개의 문제가 있다.

• 거짓 양성 오류^{False Positive}: 이미지의 일부가 얼굴이 아닌 경우는 매우 많다. 합성곱 신경망의 학습 과정 동안, 이 모델은 이런 이미지 전부를 보지 못할 것이다 (즉, 완전히 대표적인 데이터셋). 따라서 모델을 테스트하는 시점에서 수많은 거짓 양성 오류가 발생할 수 있다.

• 다른 얼굴 크기: 모든 얼굴이 30 $\times$ 30 사이즈 픽셀은 아니기에, 다른 사이즈의 얼굴의 경우 인식이 안 될 수 있다. 이 문제를 처리하는 한 가지 방법은 동일한 이미지의 멀티 스케일 (다배율)^multi-scale 버전을 만들어내는 것이다. 원래의 얼굴 인식 모델은 30 $\times$ 30 픽셀 사이즈의 얼굴만 탐지해 낼 것이다. 만일 $\sqrt 2$ 를 이미지에 배율로 적용하면, 기존의 30 $\times$ 30 이 이제는 대략 20 $\times$ 20 사이즈의 픽셀이 되기 때문에, 모델은 원본 이미지에서 더 작은 사이즈의 얼굴을 인식해 낼 수 있다. 더 큰 사이즈의 얼굴을 인식해 내기 위해서, 우리는 이미지의 배율을 축소할 수 있다. 이 과정은 비용의 절반이 배율이 적용되지 않은 원본 이미지 처리에서 발생하기 때문에 연산 비용이 저렴하다. 다른 모든 네트워크의 비용 합계가 배율이 적용되지 않은 원본 이미지 처리에 드는 비용과 동일하다. 네트워크의 크기는 한쪽 이미지 크기의 제곱과 같으므로, 이미지를 $\sqrt 2$ 로 축소하면, 실행할 네트워크의 크기가 2배 작아지는 것과 같다. 따라서 전체 비용은 $1+1/2+1/4+1/8+1/16…$, 즉 2가 된다. 멀티 스케일 (다배율) 모델은 원래의 계산 비용의 딱 두 배일 뿐이다.

멀티 스케일 (다중 스케일) 얼굴 인식 시스템

그림 2: 얼굴 인식 시스템

(그림 3) 에서 보여지는 그림들은 안면 인식기^{face detectors}의 점수를 나타낸다. 이 인식기는 크기가 20 $\times$ 20 픽셀 사이즈인 얼굴을 인식한다. (Scale 3)의 세밀한 스케일의 경우 높은 점수를 보이는 부분이 많지만, 그 부분들이 명확하지가 않다. 스케일링 계수가 올라가면 (Scale 6), 우리는 더 많이 뭉쳐져 있는 흰색 영역을 볼 수 있다. 이러한 흰색 영역은 탐지된 얼굴을 가리킨다. 이 때 우리는 비최대값 억제^{non-maximum suppression} 알고리즘을 적용해서 최종적으로 얼굴 위치를 얻는다.

그림 3: 다양한 스케일링 계수에 따른 얼굴 인식기 점수

비최댓값 억제^{Non-maximum suppression}

각각의 높은 점수를 보이는 영역마다 얼굴을 탐지해 냈을 것이다. 만일 첫 번째 인식된 얼굴과 굉장히 가까운 부근에서 더 많은 수의 얼굴이 인식된다면, 이는 단 한 개의 인식된 얼굴만 옳은 것, 나머지는 잘못된 것이라고 볼 수 있다. 비최댓값 억제를 이용해서, 우리는 중첩된 경계의 인식된 이미지 경계 박스^{bounding box} 들 중에서 가장 높은 점수를 얻는 한 개의 것만 취하고, 나머지는 버린다. 이에 따라 최적의 위치에 인식된 이미지 박스 하나만 남을 것이다.

네거티브 마이닝^{Negative mining}

마지막 섹션에서, 얼굴과 비슷하게 보이는 물체들이 많기 때문에, 훈련된 모델을 테스트 하는 과정에서 많은 수의 거짓 양성^{false positivees}을 마주칠 경우에 대해 이야기했다. 얼굴처럼 보이지만 사실은 얼굴이 아닌 물체를 모두 다 포함하는 학습 데이터셋은 존재하지 않는다. 우리는 이 문제를 네거티브 마이닝^{negative mining}을 통해 완화시킬 수 있다. 네거티브 마이닝에서는, 우리는 모델이 얼굴로 인식하지만 사실은 얼굴이 아닌 이미지 조각을 모아서 네거티브 데이터셋^{negative dataset}으로 만든다. 얼굴 이미지가 포함되지 않은 입력 데이터에 대해 모델을 학습시켜서 이러한 데이터를 모은다. 그 다음으로 우리는 이렇게 만들어진 네거티브 데이터셋에 대해 얼굴 인식 모델을 다시 학습 시킨다. 이 과정을 반복해서 우리는 거짓 양성 오류에 대한 모델의 강건성^robustness을 높일 수 있다.

의미론적 분할^{Semantic segmentation}

의미론적 분할은 입력 이미지의 모든 픽셀에 대해 범주^category를 할당하는 작업이다.

장거리 적응형 로봇 비전을 위한 CNN

이 프로젝트의 목표는 로봇이 도로와 장애물을 구분할 수 있도록 입력 이미지의 각 영역에 레이블^label 값을 할당하는 것이었다. 그림에서 녹색 부분은 로봇이 주행할 수 있는 영역이고, 빨간색 부분은 큰 잔디와 같은 장애물을 나타낸다. 이 작업을 위한 네트워크를 훈련시키기 위해서, 우리는 이미지의 일부 영역^patch을 대상으로 해당 영역이 통과 가능한 부분인지 아닌지 (녹색 또는 빨간색)에 대한 값을 직접 수동으로 할당했다. 그 다음 이렇게 레이블된 일부 영역에 대해 합성곱 신경망을 학습시켜서 해당 영역의 색상 값을 예측하도록 했다. 이 시스템이 충분히 훈련이 되고 나면, 이것을 전체 이미지에 적용해서, 이미지의 영역을 녹색 또는 빨간색으로 레이블 값을 매기도록 했다.

그림 4: 장거리 적응형 로봇 비전을 위한 CNN (DARPA LAGR 프로그램 2005-2008)

여기에는 1) 슈퍼 초록^{super green}, 2) 초록, 3) 보라: 장애물 말단 선, 4) 빨간 장애물, 5) 슈퍼 빨강, 확실한 장애물 의 다섯 개 범주가 있었다.

스테레오 레이블 (그림 4, 칼럼 2) 이미지는 로봇의 4개 카메라로 캡쳐되며, 2개의 스테레오 비전 쌍으로 그룹화된다. 스테레오 카메라 두 개 사이의 알고 있는 거리를 사용해서, 3D 공간 상의 모든 픽셀 위치는 스테레오 쌍으로 두 카메라에 나타나는 픽셀 사이의 상대적 거리로 측정값으로 추정된다. 이는 우리가 보는 물체의 거리를 추정하기 위해 우리 뇌가 사용하는 방식과 같은 과정이다. 추정된 위치 정보를 활용해서 평면이 지면에 맞춰지고 픽셀이 지면 근처에 있으면 녹색, 지면 위에 있으면 빨간 색으로 표시된다.

• **합성곱 신경망의 한계 및 동기부여^{motivation**: 스테레오 비전은 최대 10 미터까지만 작동하고 로봇을 구동하려면 장거리 비전vision이 필요하다. 그러나 합성곱 신경망의 경우 학습이 올바르게만 된다면 훨씬 더 먼 거리의 물체도 감지해 낼 수 있다.}

그림 5: 거리 정규화^{Distance-normalized} 이미지의 스케일 불변^{Scale-invariant} 피라미드

• 모델 입력으로 사용됨: 거리 정규화 이미지의 스케일 불변 피라미드를 구축하는 것은 중요 전처리 과정에 포함된다 (그림 5). 이는 이번 강의 초반에 우리가 여러 스케일의 얼굴을 탐지해 내고자 시도한 것과 유사하다.

모델 출력 (그림 4, 칼럼 3)

이 모델은 이미지의 모든 픽셀에 대해 수평선 까지 레이블을 출력한다. 이들은 다중 스케일 합성곱 신경망의 분류기 출력이다.

• 모델이 어떻게 적응해 나가는가: 로봇은 스테레오 레이블에 지속적으로 접근할 수 있고, 이는 네트워크가 재학습을 통해 새로운 환경에 적응할 수 있도록 한다. 여기서 알아둬야 할 점은 네트워크그 가장 마지막 레이어만 재학습이 이뤄진다는 것이다. 이전 레이어는 학습이 되어 고정된 상태이다.

시스템 성능

장애물의 반대편 GPS 좌표를 얻으려고 할 때, 로봇은 장애물을 멀리에서 “보고” 그 장애물을 피할 경로를 계획했다. 이는 CNN이 50-100m 떨어진 상태에서 물체를 감지해 낸 덕분이다.

한계

지난 2000년대에는, 컴퓨팅 리소스가 제한적이었다. 로봇은 초당 약 1 프레임을 처리할 수 있었는데, 이는 로봇이 자기의 경로로 진입해 걸어오는 사람에 대해 반응하기 전 1초 동안 이를 전혀 감지해 내지 못한다는 것이다. 이 한계점에 대한 해결책은 저비용 시각적 주행측정^{Low-Cost Visual Odometry} 모델이다. 이것은 신경망을 기반으로 하지 않고, ~2.5m 의 비전을 가지고 있지만, 신속하게 반응한다.

장면 파싱^{Scene Parsing}과 레이블링

이 작업에서 모델은 모든 픽셀에 대한 객체 범주 (건물, 자동차, 하늘 등.) 를 출력한다. 모델 구조는 역시 멀티 스케일(다중 스케일)이다 (그림 6).

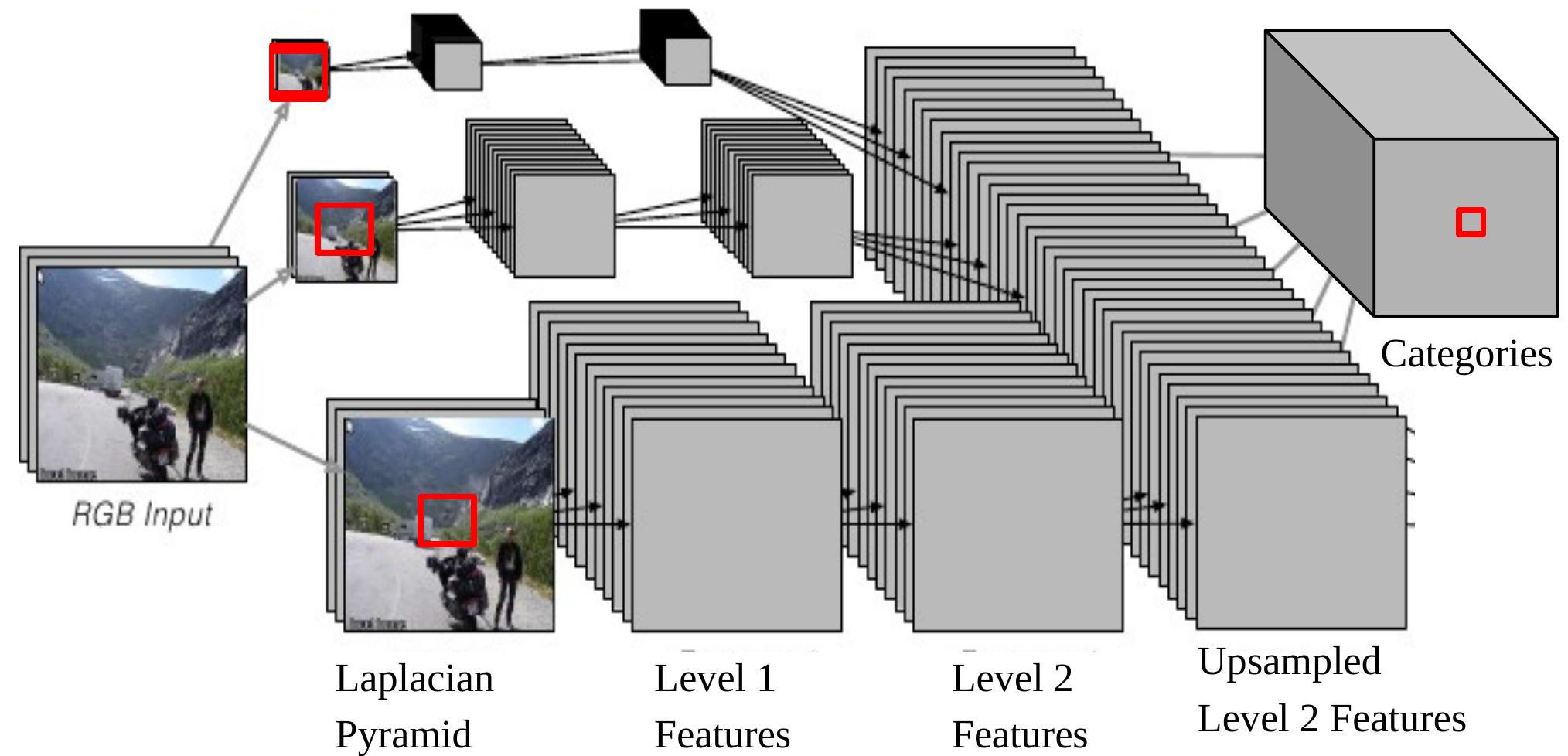
그림 6: 장면 파싱을 위한 다중 스케일 CNN

CNN 출력 하나를 입력에 다시 투영하면, 이는 $46\times46$ 크기의 라플라시안 피라미드^{Laplacian Pyramid}하단의 입력 윈도우에 해당한다. 이는 우리가 It means we are 중앙 픽셀의 범주를 결정하기 위해 $46\times46$ 픽셀의 맥락^context을 사용하고 있음을 의미한다.

그러나, 가끔 이 맥락 사이즈^{context size}는 더 큰 개체의 범주를 결정하기에 충분하지 않다.

멀티 스케일 방식은 추가적으로 다시 스케일된 이미지를 입력으로 제공하면서 더 넓은 비전을 가능하게 한다 그 과정은 다음과 같다:

1. 동일한 이미지를 각각 2배, 4배 줄인다.
2. 이 두 개의 추가로 크기 조정된 이미지들은 동일한 ConvNet (동일한 무게, 동일한 커널)에 입력되고 우리는 또 다른 레벨 2 특징값^{Level 2 Featrues} 두 세트를 얻는다.
3. 이 특징값을 업-샘플^Upsample 해서 원본 이미지의 레벨 2 특징값과 동일한 사이즈가 되도록 한다.
4. 이렇게 (업-샘플된) 세 개 세트의 특징값을 쌓아서 분류기에 입력한다.

이제 1/4 크기로 재조정된 이미지에서 나온 가장 큰 유효한 결과물의 크기는 is $184\times 184\, (46\times 4=184)$ 이다.

성능: 어떠한 후처리 과정^{post-processing}과 프레임별 실행이 없어도, 모델은 표준 하드웨어 상에서도 매우 빠르게 실행된다. 학습하는 데이터의 크기는 다소 작은 편이지만 (2k~3k), 모델의 성과는 여전히 기록적인 수준이다.