합성곱 이해와 자동 미분 엔진

1D 합성곱 이해

데이터 희소성, 정상성 그리고 합성성(구성)에 대하여 알아보기 위하여, 이번 파트에서는 합성곱에 대하여 논하고자 한다.

지난 시간 언급했던 행렬 $A$를 사용하는 대신, 이 행렬의 폭을 커널 사이즈 $k$로 바꿀 것이다. 그러므로, 행렬의 각 행은 하나의 커널이다. 쌓기와 이동(그림 1 참조)을 이용하여 커널을 바꿀 수 있게 되며, 그렇게 되면 높이가 $n-k+1$인 $m$개의 층위를 얻을 수 있다.

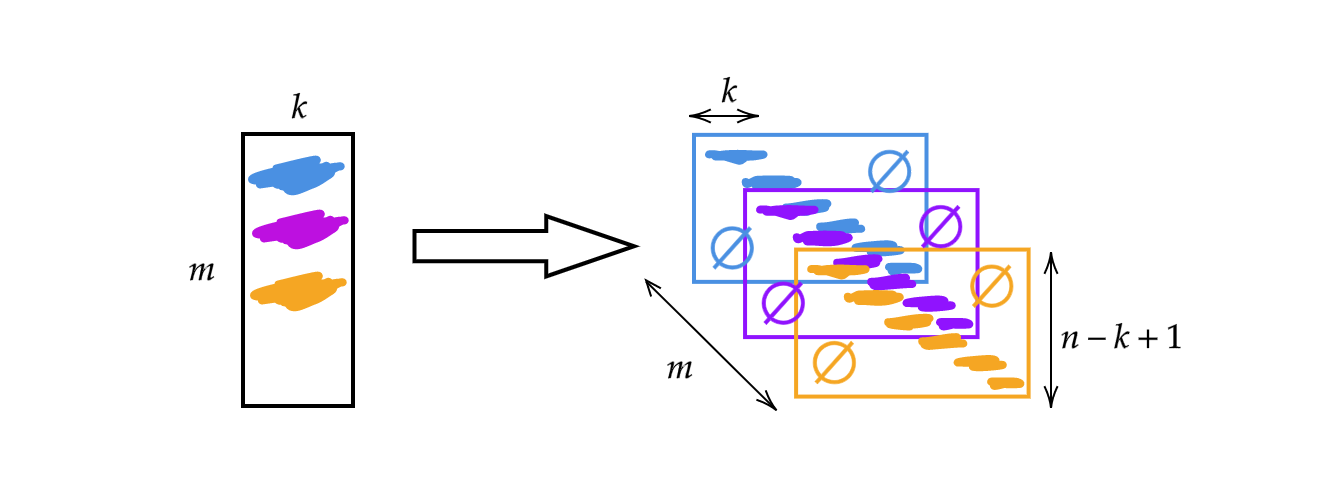
그림 1: 1D 합성곱 개념도

출력 결과는 $n-k+1$ 사이즈에 $m$개의 층으로 이루어진 벡터이다.

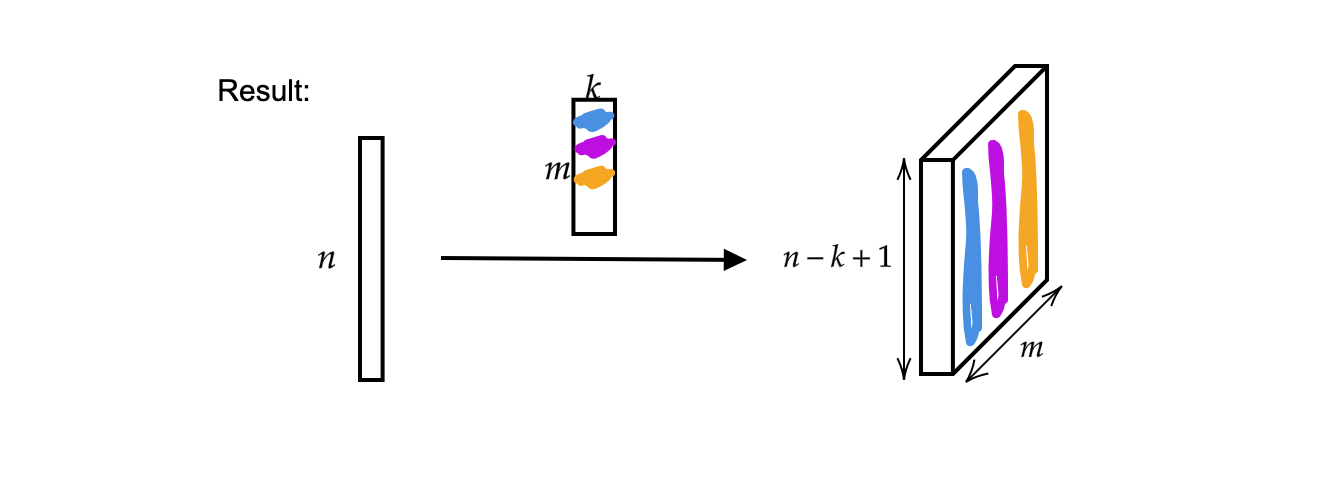
그림 2: 1D 합성곱 결과

여기에 단일 입력 벡터는 단음^monophonic 신호로 보일 수 있다.

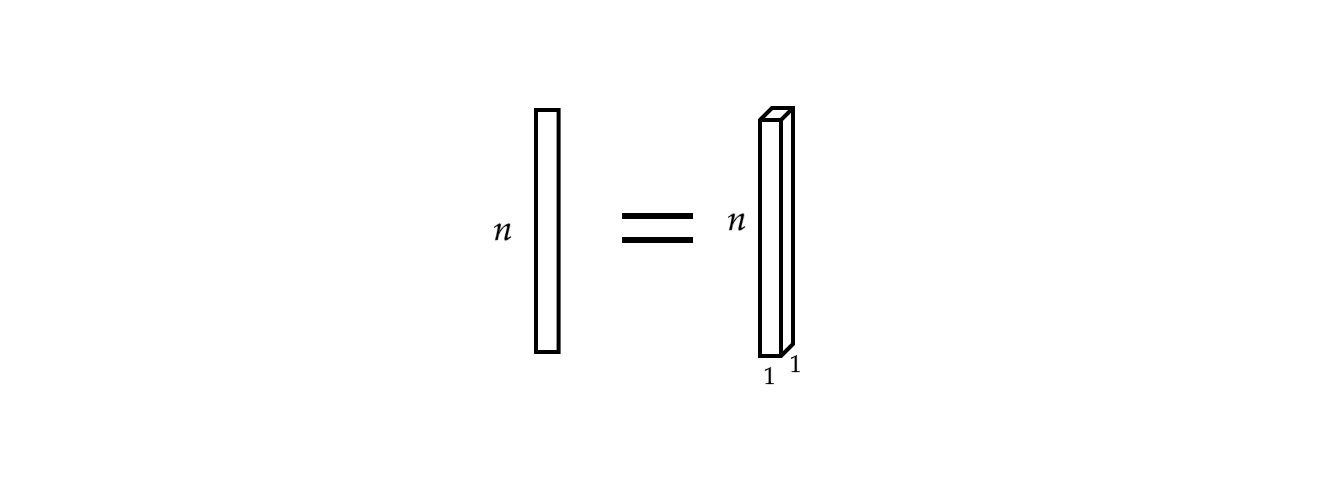
그림 3: 단음 신호

이제, 입력 벡터 $x$는

위와 같이 맵핑한다.

$\Omega$는 $\mathbb{N}^1$안에 포함된 부분 공간이고(이는 1차원 신호이기 때문에, 1차원 도메인을 가진다.) 이 때, 채널 수 $c$는 $1$이며 $c = 2$일 때, 입체 음향^stereophonic 신호가 된다.

1D 합성곱에 대하여, 우리는 스칼라 곱을 커널에 따라 계산할 수 있다. (그림 4 참조)

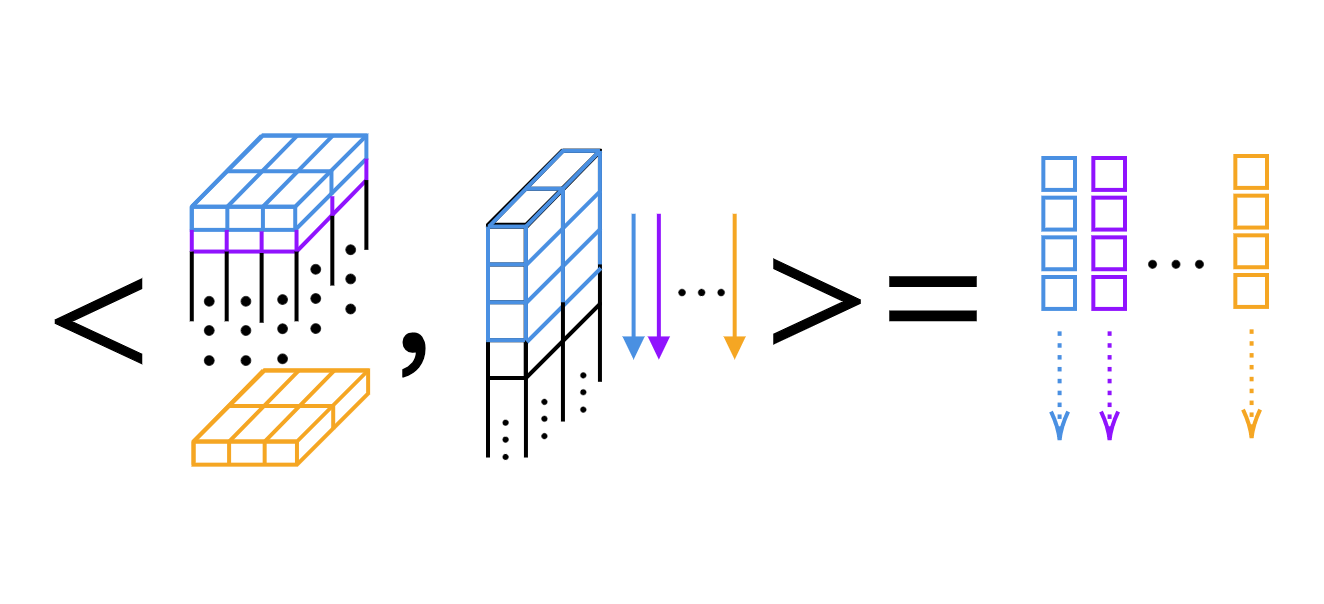
그림 4: 1D 합성곱의 층위에 따른 스칼라 곱

파이토치에서의 커널 차원과 출력 결과 폭

팁: 우리는 I파이썬^IPython에서 물음표를 이용하여 각 기능들에 대한 설명을 확인할 수 있다. 예를 들면, 다음과 같다.

Init signature:
nn.Conv1d(
	in_channels,           # 입력 이미지 내에 있는 채널 수
	out_channels,          # 합성곱에 의해 만들어진 채널 수
	kernel_size,           # 커널의 회전 크기
	stride=1,              # 합성곱 스트라이드
	padding=0,             # 입력 이미지 양쪽에 추가된 제로-패딩
	dilation=1,            # 커널 요소들 사이 간격
	groups=1,              # 입력 데이터에서 결과 데이터까지 이어지는 연결 단위 수
	bias=True,             # 만일 `참`이라면, 결과 데이터에 학습할 수 있는 편향값 추가
	padding_mode='zeros',  # `0`과 `순환` 수락
)

1D 합성곱

우리는 $2$-채널(입체 음향^stereophonic 신호)에서 커널사이즈 $3$, 스트라이드 $1$인 $16$-채널($16$개의 커널)까지 이르는 $1$차원 합성곱을 가지고 있다. 이렇게 되면 우리는 $2개$의 두께(층위)와 길이가 $3$인 $16$개의 커널을 가지게 된다. 여기서 입력 신호는 배치사이즈가 $1$(단일 신호)에 $2$ 채널과 $64$ 샘플을 가지고 있다고 가정하자. 결과에 해당하는 출력 결과 층위는 하나의 신호, $16$개의 채널을 가지며, 신호의 길이는 %62$ ($=64-3+1$)이다. 또한, 우리가 편향값 사이즈를 출력한다면, 편향값 사이즈가 $16$이라는 사실을 알아낼 것인데, 이는 가중치 당 하나의 편향값을 가지기 때문이다.

conv = nn.Conv1d(2, 16, 3)  # 2채널(입체 신호), 사이즈 3의 16커널
conv.weight.size()          # 출력: torch.Size([16, 2, 3])
conv.bias.size()            # 출력: torch.Size([16])

x = torch.rand(1, 2, 64)    # 사이즈 1, 2채널, 64 샘플인 배치
conv(x).size()              # 출력: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2채널, 사이즈 5의 16커널
conv(x).size()              # 출력: torch.Size([1, 16, 60])

2D 합성곱

먼저, 입력 데이터를 높이 $64$, 폭 $128$의 채널 $20$개로 이루어진 하나의 예제로서 정의한다. (즉, 초분광 이미지를 사용한다.) 2D 합성곱은 입력 데이터와 크기가 $3 \times 5$인 $16$개의 커널로 구성된 $20$개의 채널을 갖는다. 합성곱 이후, 출력 데이터는 높이 $62$ $(=64-3+1)$, 폭 $124$ $(=128-5+1)$인 $16$개의 채널로 만들어진 하나의 샘플을 가진다.

x = torch.rand(1, 20, 64, 128)    # 1 샘플, 20채널, 높이 64, 폭 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20채널, 16커널, 커널 사이즈 $3\times 5$
conv.weight.size()                # 출력: torch.Size([16, 20, 3, 5])
conv(x).size()                    # 출력: torch.Size([1, 16, 62, 124])

만약 차원수를 동일하게 맞추기를 원한다면, 패딩을 이용하면 해결할 수 있다. 위 코드에 이어 합성곱 함수에 새로운 매개 변수 값을 추가할 수 있다.: stride=1과 padding=(1,2)인데, 이는 $y$축 방향(위로 $1$, 아래로 $1$)으로 $1$을 의미하고, $x$축 방향으로 $2$를 의미한다. 그러면 출력 신호는 입력 신호와 비교하여 동일한 크기에 있게 된다. 2D 합성곱을 실행할 때, 커널 모음을 저장하는데 필요한 차원 수는 $4$이다.

# 20채널, 사이즈 $3\times5$ 16커널, 스트라이드 1, 패딩값 1,2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # 출력: torch.Size([1, 16, 64, 128])

자동 경사는 어떻게 돌아갈까?

이번에는 토치를 이용하여 텐서 이상의 모든 연산을 확인함으로써, 편도함수를 구할 수 있다.

• 경사 축적이 가능한 형태의 $2\times2$ 텐서 $\boldsymbol{x}$를 만든다.
• $\boldsymbol{x}$의 모든 원소들로부터 2씩 줄이고 $\boldsymbol{y}$를 얻는다; (y.grad_fn을 출력하면, <SubBackward0 object at 0x12904b290>이라는 메시지를 얻는데 여기서 y는 $\boldsymbol{x}-2$라는 뺄셈 연산에 의해 생성된 결과라는 것을 의미한다. 또한 원래의 텐서값을 얻기 위하여 y.grad_fn.next_functions[0][0].variable를 이용할 수 있다.)
• 연산을 더 수행한다: $\boldsymbol{z} = 3\boldsymbol{y}^2$;
• $\boldsymbol{z}$의 평균을 계산한다.

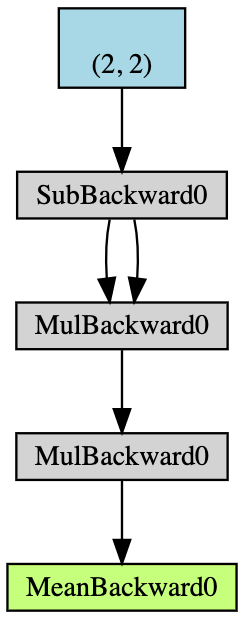
그림 5: 자동-경사 예제 순서도

역전파는 경사를 계산하는데 쓰인다. 이 예제에서, 역전파 과정은 경사 $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$를 계산하는 것으로 보일 수 있다. $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$를 확인 차원에서 손으로 계산한 후, a.backward()는 우리가 계산했던 x.grad와 같은 값이라는 것을 알 수 있다.

손으로 계산한 역전파 계산 과정은 아래와 같다.

파이토치에서 편도함수를 이용할 때마다, 원래 데이터와 동일한 형태^shape를 얻는다. 하지만 정확한 야코비안^Jacobian 형태는 이것의 전치행렬^transpose이 되어야 한다.

머리부터 발끝까지

지금 우리에게 $1\times3$ 벡터 $x$가 있고, $y$에 $x$를 2를 곱한 값을 할당하고, $y$의 놈^norm이 $1000$보다 작아질 때까지 계속 $y$의 값을 두배로 만드는 ($y\times 2$) 작업을 계속한다. $x$에 대하여 우리가 가진 무작위성 때문에, 연산 과정이 끝날 때 반복 횟수를 바로 알 수 없다.

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

그러나, 우리는 경사값을 알고 있기 때문에 이를 쉽게 추론할 수 있다.

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

추론에 대하여 살펴보면, 아래에 코드에 나와있듯이 requires_grad=True를 사용하여 경사 축적을 추적해 나갈 수 있다. 만약 $x$나 $w$ 선언에서 requires_grad=True를 빠뜨리고 $z$상의 backward()를 호출하면, $x$ 또는 $w$에 축적된 경사가 없기 때문에 런타임 오류가 발생한다.

# x와 w 모두 경사 축적이 가능하다.
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

그리고 이 경사 축적을 생략하고자 with torch.no_grad()를 쓸 수 있다.

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# 모든 토치 텐서는 `torch.no_grad()`를 사용함으로써 경사 축적을 갖지 않는다.
with torch.no_grad():
    z = w @ x

try:
    z.backward()  # z가 경사 축적을 갖지 않으므로, 파이토치는 여기서 오류를 무시하고 넘어갈 것이다.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

그 외 – 맞춤 경사

또한 기초적인 수치 연산 대신, 신경 그래프로 연결될 수 있는 자체 정의 모듈이나 함수들을 만들 수 있다. 주피터 노트북에서 작성한 코드는 [여기서]https://github.com/Atcold/pytorch-Deep-Learning/blob/master/extra/b-custom_grads.ipynb) 확인할 수 있다.

이를 위하여 torch.autograd.Function을 상속받아야 하고 forward()와 backward() 함수를 재정의해야 한다. 예를 들어, 신경망을 학습시키고자 할 때, 순방향 진행 경로를 확보하고, 이 모듈을 코드의 어느 지점에서든 사용할 수 있도록 출력에 대한 입력의 편도함수를 알아야 한다. 그 다음, 역전파^{backpropagation}(연쇄규칙)^{chain rule}을 통해 출력값에 대한 편도함수를 아는 어느 곳에나 이 모듈을 작업 체인에 연결할 수 있다.

이 경우, notebook 안에 add, split 그리고 max 세 가지 맞춤 모듈이 있다. 맞춤형 추가 모듈은 예를 들면 아래와 같다.

# 추가 모듈 맞춤
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx는 우리가 역방향 연산을 저장할 수 있는 위치의 맥락이다.        
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # 입력값이 순방향으로 정렬된 경사값을 리턴해야 한다.(단, ctx는 제외)
        return grad_x1, grad_x2

우리가 두 가지 추가 사항을 가지고 출력 결과를 얻는다면, 이와 같은 순방향 함수를 덮어써야 한다. 그리고 역전파 단계로 내려갈 때, 경사는 양쪽 모두에 복사되고, 따라서 복사를 통해 역방향 함수를 덮어쓰게 된다.

split과 max에 대해서는 notebook에서 우리가 어떻게 순방향, 역방향 함수를 덮어씌우는지에 대한 코드를 살펴볼 것을 권한다. Split과 동일한 것에서 출발한다면, 경사를 구하는 단계로 내려갈 때, 우리는 그것들을 추가하거나 더해야 한다. argmax의 경우, 가장 높은 것의 인덱스 값을 선택하므로, 가장 높은 것의 인덱스 값은 반드시 $1$이고 아닌 것은 $0$이어야 한다. 다양한 맞춤 모듈에서 우리는 이 모듈의 순방향 경로를 우리가 덮어써야 한다는 것과 이들이 역방향 함수에서 어떻게 경사를 다루는지 기억해야 한다.