최적화 II

적응적 방법들

현재 많은 기계학습 문제들에서 SGD와 모멘텀을 함께 사용한다는 건 최첨단의 최적화 기법이다. 하지만 열악한 조건의 문제들(SGD가 동작하지 않을때)에 유용하도록 수년간 발전되어온, 일반적으로 적응적 방법론^{Adaptive Methods}이라 불리우는 다른 방법들도 있다.

공식화한 SGD에서 네트워크 상 모든 개별 가중치는 동일한 학습률^{learning rate}을 사용한 공식을 통해 갱신된다. (글로벌 $\gamma$) 이제 우리는 적응적 방법으로 개별적인 가중치를 위한 학습률을 적용할 것이다. 이를 위해, 각 가중치가 사용된 경사로부터 정보를 얻은 정보를 이용한다. 네트워크는 실제 적용시, 종종 다른 부분들이나 다른 구조를 갖게 된다. 그 예로, CNN의 앞부분은 큰 이미지들 대비 매우 얕은 합성곱 계층들이고, 네트워크의 뒷부분은 작은 이미지들 대비 많은 양의 채널을 가진 합성곱 계층들일 것이다.

이 두 개의 연산은 매우 다르기 때문에 네트워크의 초반부에서 잘 동작하던 학습률이 네트워크 후반부에서는 잘 동작하지 않을 수 있다. 이는 계층별로 적응적 학습률^{adaptive learning rates}이 유용하리라는 뜻이다. 네트워크 후반부의 가중치들(아래 그림 1에서는 4096)은 출력값에 직접적으로 작용하는데, 매우 강한 영향력을 주기 때문에 더 작은 학습률을 줘야한다. 반대로, 앞부분의 가중치들은 더 작고 개별적인 영향력을 출력값에 주는데, 무작위로 초기화 되었다면 더더욱 그러하다.

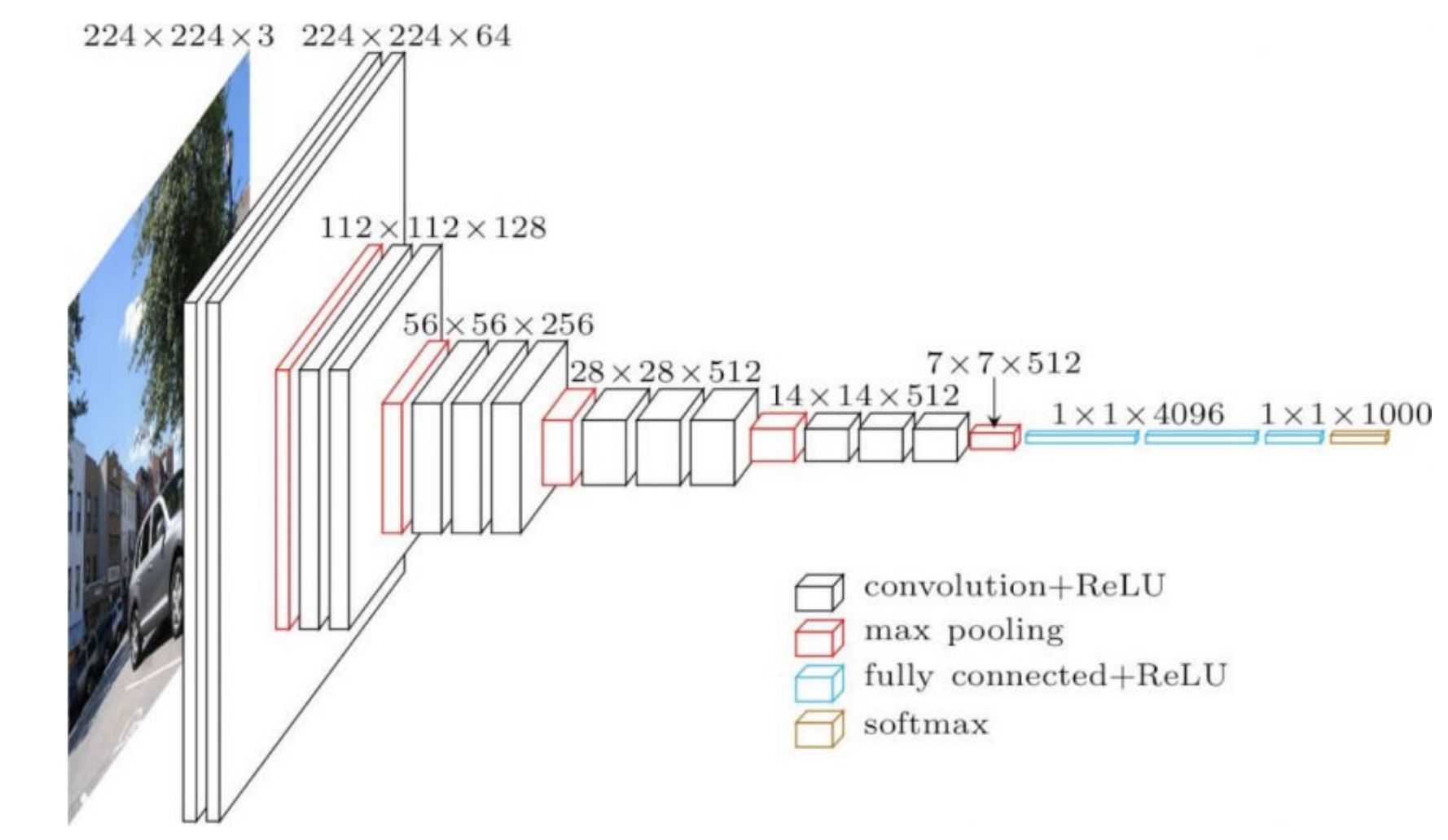
그림 1: VGG16

RMSprop

평균 제곱근 전파의 핵심 아이디어는 경사의 평균 제곱근^{root-mean-square}으로 경사를 정규화하는 것이다. 아래 공식에서 경사의 제곱은, 벡터의 각 요소마다 제곱되었음을 나타낸다.

$\gamma$가 전역 학습률^{global learning rate}이기에, $\epsilon$은 머신 $\epsilon$(역주. 머신 엡실론. 부동 소수점 연산에서 1보다 큰 수들 중 가장 작은 수와 1과의 차이 [출처])에 가까운 값이고 ($10^{-7}$ 또는 $10^{-8}$ 순서로) (0으로 나눠질때 발생하는 에러를 방지하기 위해서다), $v_{t+1}$는 이차 모멘트^{2nd moment estimate}에 대한 추정이다.

우리는 이 노이즈의 양을 추정하기 위해 지수 이동 평균^{exponential moving average}을 통해 $v$를 갱신한다. (시간이 지남에 따라 달라질 수 있는 노이즈 양의 평균을 유지하는 표준 방법이다.) 새로운 값일수록 더 많은 정보를 제공하기에 더 큰 가중치들을 줄 필요가 있다.

이를 하는 방법 중 하나는 예전 값들을 지수적으로 줄여나가는 것이 있다. $v$ 계산에 이용되는 오래된 값들은 각 단계마다 0과 1사이 값을 갖는 $\alpha$ 상수에 의해 압축된다. 감쇠^dampens는 예전 값들이 지수 이동 평균에서 더 이상 중요하지 않게 될때까지 이루어진다. 원 방법은 비중심 이차 모멘트^{non-central second moment}의 지수 이동 평균을 보존하므로, 여기에서 평균값을 빼줄 필요는 없다.

이 이차 모멘트는 경사를 원소별로 정규화하는데에 사용된다. 원소별 정규화는, 경사의 모든 개별 요소가 이차 모멘트 추정의 제곱근으로 나누어진다는 의미이다.

만약 경사의 예상되는 값이 작다면, 이 과정은 표준 편차에 의해 경사가 나누어지는 것과 비슷하다. (역주. 백색화) 분모에 작은 $\epsilon$을 사용하더라도 발산하지 않는데, $v$가 매우 작을 때 모멘텀 또한 매우 작을 것이기 때문이다.

아담

아담, 또는 적응적 모멘트 추정Adaptive Moment Estimation은 RMSprop에 모멘텀을 더한 것으로, 더 일반적으로 쓰이는 방법이다. 모멘텀 갱신은 지수 이동 평균으로 변환될 수 있고, $\beta$를 사용할 때 학습률을 바꿔줄 필요가 없다. RMSprop에서처럼, 우리는 제곱된 경사의 지수 이동 평균을 여기에 사용할 것이다.

$m_{t+1}$이 모멘텀의 지수 이동 평균일때의 공식은 아래와 같다.

초반부 반복작업동안 이동 평균을 편향되지 않게 잡아주는 편향 보정에 대해서는 여기에 언급되어 있지 않다.

실용적 측면

신경망을 훈련시킬 때, SGD는 종종 훈련 과정에서 시작부터 잘못된 방향으로 가는 반면, RMSprop은 올바른 방향으로 가려고 한다. 하지만 RMSprop도 보통의 SGD처럼 노이즈가 있다. 국소 최소점에 가까워지면, 최적점 주변에서 크게 튀곤 한다.

단순히 SGD에 모멘텀을 더할때처럼, ADAM에서도 비슷한 형태의 발전을 생각할 수 있다. 해결책에서 노이즈가 끼지 않은 추정이라 좋고, 보통 아담^ADAM을 RMSprop보다 더 많이 추천한다.

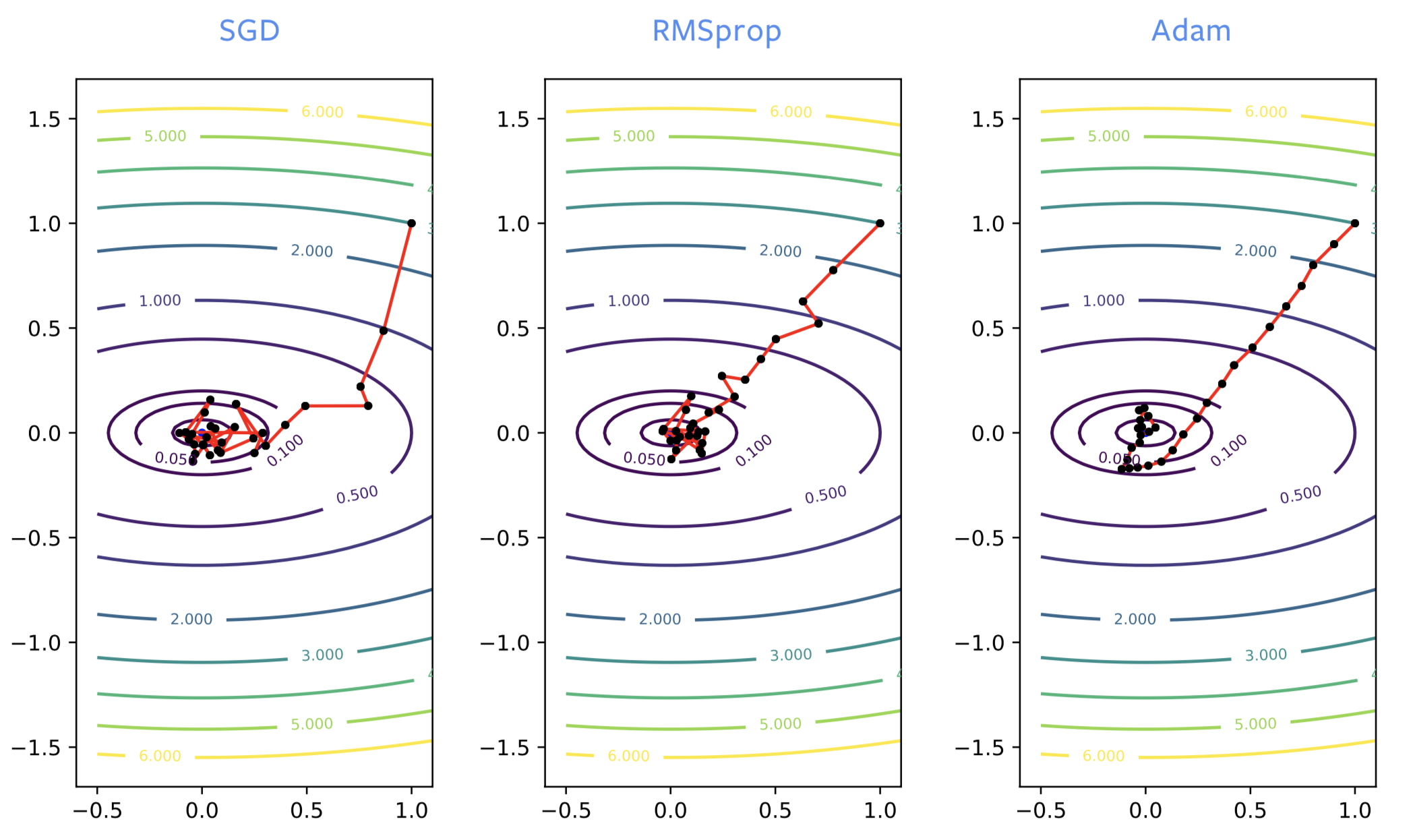
Figure 2: SGD vs RMSprop vs ADAM

아담은 언어 모델들을 사용하기 위해, 일부 네트워크 훈련을 위해 필요하다. 신경망을 최적화한다면 일반적으로 모멘텀을 더한 SGD 또는 아담이 선호되지만, 아담의 이론들은 논문에서 빈약하게 이해되었기에 결점들 역시 존재한다.

• 이 방법이 수렴하지 않는다는 매우 간단한 실험 문제들이 나올 수 있다.

• 일반화^{generalization} 오류를 낼 수 있다고 알려져있다. 학습 데이터에 대한 손실값이 0이 되도록 훈련된 신경망이 있다면, 이 신경망은 학습 과정 동안 본 적 없는 여타 데이터에 대해서는 0의 손실값을 내놓을 수 없다. 이는 꽤 흔한 현상으로 특히 이미지 문제들에서 그러한데, SGD를 사용할때보다 더 나쁜 일반화의 오류들을 얻는다. 인자들은 최근접 국소 최저점, 아담에서 노이즈가 덜 있는 부분, 또는 그 구조를 찾는 걸 포함할 수 있는 예시가 있다.

• SGD가 2개의 버퍼들을 사용하는데 반해, 아담에서는 3개의 버퍼들을 유지해야 한다. 여러 기가바이트 크기의 모델을 훈련시키려는게 아니라면, 그다지 중요하지는 않은 부분이다.
• 1개가 아닌 2개의 모멘텀 매개변수들이 조정^tuned되어야 한다.

정규화 계층

최적화 알고리즘들을 개선하는 것보다, 네트워크의 정규화 계층이 신경망 구조 자체를 향상시킨다. 이는 기존 계층들 사이에 있는 추가 계층들로, 목표는 최적화와 정규화 성능의 향상이다.

신경망에서, 우리는 일반적으로 선형 연산들의 비선형 연산들을 대안으로 한다. 비선형 연산들은 ReLU같은 활성화 함수로도 알려져 있다.

우리는 정규화 계층을 선형 계층들 이전이나, 활성화 함수들 뒤에 둔다. 가장 일반적인 형식은 아래 그림처럼 선형 계층들과 활성화 함수들 사이에 두는 것이다.

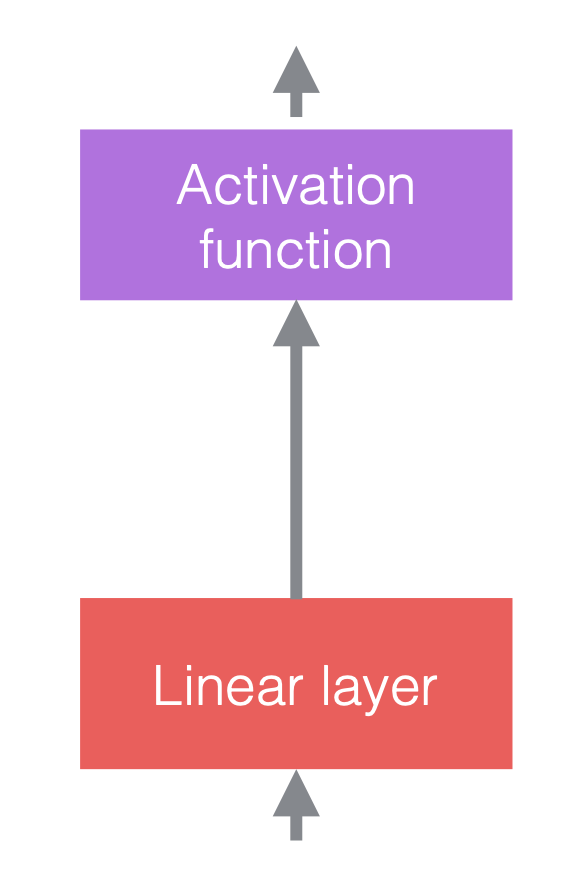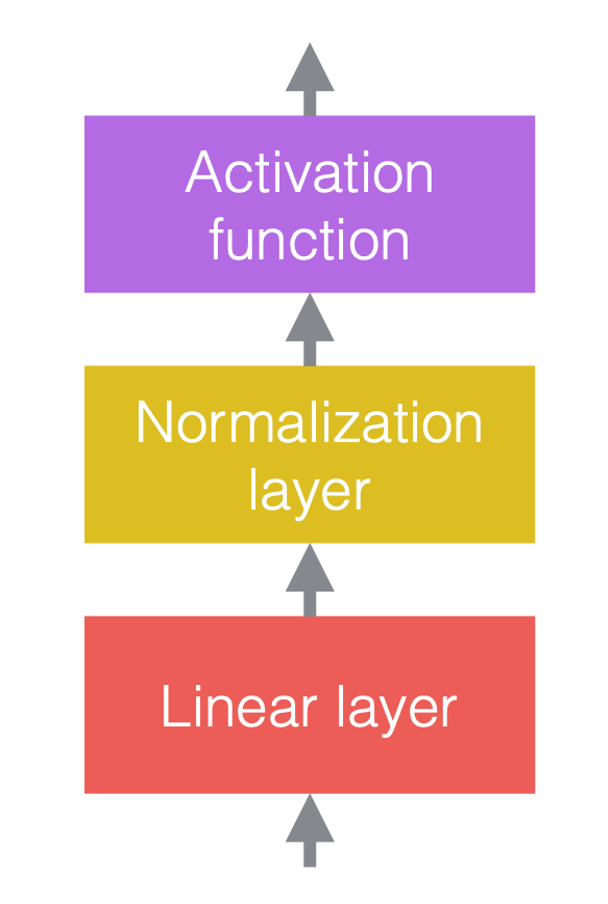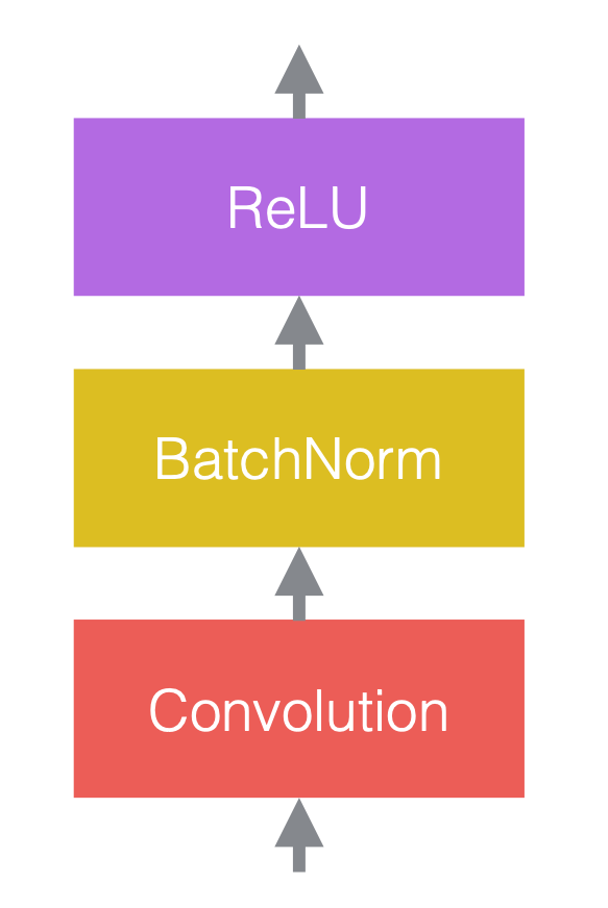(a) 정규화 추가 이전	(b) 정규화 추가 이후	(c) CNN 예시

그림 3(c)에서 합성곱은 배치 정규화나 ReLU 뒤에 따라 나오는 선형 계층이다.

알아두어야 할 점은 정규화 계층들은 이를 통과하는 데이터에 영향을 끼치지만, 제대로 구성된 가중치들이 있다면 네트워크의 힘 자체를 바꿀 수는 없다. 정규화되지 않은 네트워크는 여전히 정규화된 네트워크와 동일한 출력값을 내놓는다.

정규화 작용

이는 정규화의 일반적인 표기법이다:

$x$는 입력 벡터, y는 출력 벡터이고, $\mu$는 $x$ 평균의 추정이다. $\sigma$는 $x$ 표준 편차(std)의 추정이며, $a$는 학습가능한 규모 인자^{learnable scaling factor}, 그리고 $b$는 학습가능한 편향 항^{learnable bias term}이다.

학습가능한 매개변수들 $a$와 $b$가 없으면, 출력 벡터의 분포 $y$는 평균 0, 표준 편차 1로 고정이 된다. 규모 인자 $a$와 편향 항인 $b$는 네트워크의 표현력을 유지해준다. 다른 말로는, 출력값은 여전히 어떤 특정한 범위라도 넘어설 수 있다는 것이다. $a$와 $b$는 정규화를 되돌리지 않는데, 이 둘은 학습가능한 매개변수들이고 $\mu$와 $\sigma$보다 더 안정적이기 때문이다.

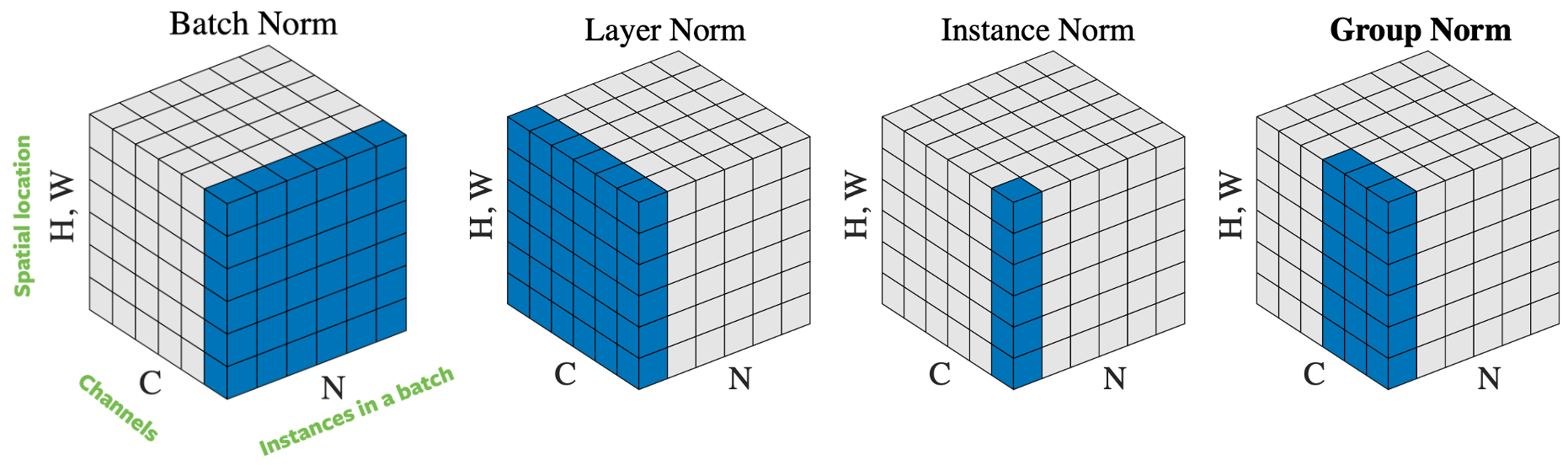
그림 4: 정규화 연산.

입력 벡터를 정규화하는데에는, 어떻게 샘플을 선택하느냐에 기반한 몇 가지 방법들이 있다. 그림 4는 세로 $H$ 가로 $W$ 그리고 $C$개의 채널을 가진 이미지 $N$개의 미니배치 하나로, 4개의 각기 다른 정규화 접근법을 보여주고 있다:

• 배치 정규화: 정규화는 입력값에서 하나의 채널에만 적용이 된다. 이는 첫번째로 제안되었고 가장 잘 알려진 접근방식이다. 더 많은 정보가 필요하다면 어떻게 ResNet을 훈련시키는가 7: Batch Norm을 읽어보자.
• 계층 정규화: 정규화는 한 이미지의 모든 채널들에 걸쳐 적용된다.
• 인스턴스 정규화: 정규화는 오로지 한 이미지에서 한 채널에만 적용된다.
• 그룹 정규화: 정규화는 하나의 이미지, 그리고 다수의 채널에 걸쳐 적용된다. 예를 들자면, 채널 0과 채널 9가 하나의 그룹이면, 채널 10과 채널 19는 다른 그룹으로 만드는 식의 방식이다. 실제로, 그룹 크기는 거의 항상 32이다. 이는 아론 데파지오^{Aaron Defazio}에 의해 추천된 접근법으로, 문제없이 SGD와 좋은 성능을 내주고 있다.

실제로 배치 정규화와 그룹 정규화는 컴퓨터 비전 문제들에서 잘 동작하고, 계층 정규화와 인스턴스 정규화는 언어 문제들에서 많이 사용되고 있다.

왜 정규화가 도움이 되는가?

실전에서 정규화가 잘 동작함에도, 효율성의 원인에 대해선 여전히 논쟁중이다.

원래 정규화는 내부 공변량 변화^{internal covariate shift}를 줄이기 위해 제안되었으나, 몇몇 학자들이 실험에서 그것이 잘못되었음을 증명했다. 그럼에도 정규화는 확실하게 다음과 같은 요소들의 조합이다:

• 정규화 계층이 있는 네트워크는 더 큰 학습률을 사용할 수 있어서 최적화하기 더 쉽다. 정규화에는 신경망의 훈련 속도를 높여주는 최적화 효과가 있다.
• 평균과 표준편차의 추정값들은 배치 샘플들의 무작위성으로 인해 노이즈값을 끼고 있다. 이 부수적인 “노이즈”는 일부 사례들에서 더 나은 정규화를 내놓기도 한다. 정규화는 제약 효과가 있다.
• 정규화는 초기 가중치값의 영향을 줄인다.

결론적으로, 정규화는 “덜 신경쓰게” 만든다 - 대부분의 신경망과 조합할 수 있고, 조건이 얼마나 빈약한지 생각할 필요없이 훈련시킬 수 있다.

실 고려사항들

역전파가 평균과 표준 편차의 계산을 통해 이루어진다는 건, 정규화의 적용방법 만큼이나 중요하다: 그렇지 않을 경우 네트워크는 훈련하다 발산해버린다. 역전파 계산은 어렵고 오류도 발생하기 쉬운데, 파이토치^PyTorch는 이를 자동으로 계산해준다. 파이토치에 있는 두 정규화 계층 클래스는 아래와 같다:

torch.nn.BatchNorm2d(num_features, ...)
torch.nn.GroupNorm(num_groups, num_channels, ...)

배치 정규화는 첫번째로 개발되었고 가장 널리 알려진 방법이다. 하지만, 이것 대신 아론 데파지오는 그룹 정규화를 사용하기를 추천한다. 더 안정적이고, 이론적으로 더 간단하며, 대개 더 나은 성능을 보이기 때문이다. 기본적인 그룹 크기는 32로 하는 것이 좋다.

참고로 배치 정규화와 인스턴스 정규화는 사용되는 평균/표준편차가 매번 신경망이 평가될 때 마다 다시 계산되지 않고 학습 이후 값이 고정된다. 이는 하나의 훈련 샘플에만 정규화를 적용하는 그룹 정규화와 계층 정규화에는 필요없다.

최적화의 죽음

우리는 가끔 구현해놓은 것을 어떻게 좋게 만들 수 있는지 알지 못하는 무지의 영역에 부딪히고는 한다. 그 예로 MRI^{자기 공명 영상}분야에 심층 신경망을, MRI 이미지 재구성을 가속하기 위해 사용하는 것이 있다.

그림 5: 때때로 그건 정말로 동작한다!

MRI 재구성

전통적인 MRI 재구성 문제에서, 가공되지 않은 데이터는 MRI 기계로부터 오고, 이미지는 간단한 파이프라인/알고리즘을 사용해 이 가공되지 않은 데이터에서 재구성된다. MRI 기계들은 2 차원의 푸리에 영역, 시간마다(몇 밀리초 마다) 행 하나 또는 열 하나로 데이터를 담는다.

이 가공되지 않은 입력값은 빈도와 단계^phase 채널의 구성으로 되어있고, 그 값은 특정 빈도수와 단계를 가진 사인파^{sine wave}의 규모로 나타난다. 간단하게 말하자면, 이는 실수와 허수 채널을 가진 복소수 값으로 된 이미지로 생각할 수 있다.

만약 역 푸리에 변환^{inverse Fourier transform}을 이 입력값에 적용한다면, 다른말로는 모든 사인파들에 그들의 가중치를 곱한 값들을 더해서, 원래의 해부 이미지를 얻는다.

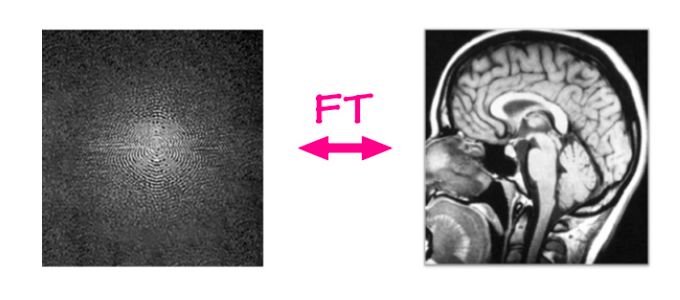
그림 6: MRI 재구성

선형 사상은 현재 존재하는 푸리에 영역^{Fourier domain}을 이미지 영역^{image domain}으로 보내는데, 꽤 효과가 좋다. 이미지가 얼마나 크던지 간에 말 그대로 밀리초밖에 걸리지 않는다. 하지만 여기서 생각해 볼 것은, ‘이보다 더 빠르게 만들 수 있을까?’이다.

가속화된 MRI

이제 우리가 새롭게 풀어야 할 문제는 가속화된 MRI이다, 물론 가속화되었다는 건 MRI 재구성을 훨씬 빠르게 만들거라는 뜻이다. 장비들은 더 빠르게 동작하면서도, 동일한 품질의 이미지들을 만들어낼 수 있어야 한다. 이를 해내는 한 가지 방법이자 가장 성공한 방법은 바로 MRI 스캔으로부터 모든 열^columns을 담지는 않는 것이다.

우리는 일부 열을 무작위로 거를 수 있는데, 즉 이미지 전반에 걸쳐 많은 정보를 담고 있는 중간열들을 포착하는건 유용하지만, 그 주변부에서는 무작위로 포착하게 된다.

문제는 이미지를 재구성하기 위해 선형 사상을 더 이상 쓸 수 없다는 점이다. 그림 7에서 가장 오른쪽에 있는 이미지는 서브샘플된^subsampled 푸리에 공간에 선형 사상을 적용한 결과물이다. 이 방법이 쓸만한 결과물을 내지 못한다는 건 명백하니, 조금 더 똑똑한 것을 시도해보자.

그림 7: 서브샘플링된 푸리에 공간에서의 선형 사상

압축 센싱

오랫동안 이론 수학에서 가장 큰 혁신 중 하나는 압축 센싱^{compressed sensing}이었다. Candes et al. 논문은 이론적으로, 서브섬플된 푸리에-영역 이미지로부터 완벽한 재구성을 할 수 있음을 보여주었다. 다른 말로, 우리가 재구성 하려는 신호가 희소하거나 희소하게 구조화 되었다면, 더 적은 수의 계측만으로도 완벽한 재구성이 가능하다는 것이다.

하지만 이를 위해서는 몇가지 실제적인 요구사항들이 있다 - 우리는 무작위로 샘플링을 할 필요가 없다, 오히려 우리는 모순되게^incoherently 샘플을 할 필요가 있다 - 그러나 실제로, 사람들은 결국 무작위로 샘플링하게 된다.

추가로, 전체 열을 샘플링하든 절반 정도의 열이든 동일한 시간이 소요되므로, 우리는 전체 열을 샘플한다.

다른 조건은 이미지에서 희소성을 갖는게 필요하다. 이미지에서 희소성이란 수많은 0 값 또는 검은 픽셀들을 의미한다.

가공되지 않은 입력값은 파장 분해^{wavelength decomposition}를 할 경우, 희소하게 나타낼 수 있다. 하지만 이 분해 작업을 해도 대략 희소하게는 해주지만, 이미지를 정확하게 희소하게 해주진 못한다. 그래서, 이는 꽤 괜찮은 접근법이지만 그림 8에서도 볼 수 있다시피 완벽한 재구성은 아니다. 하지만, 만약 입력값이 파장 영역^{wavelength domain}에서 매우 희소하다면, 완벽한 이미지를 얻을 수 있을 것이다.

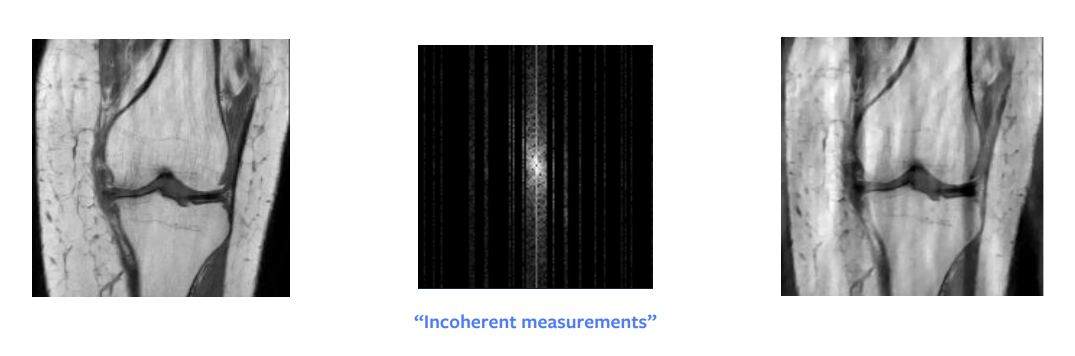
그림 8: 압축 센싱

–>

최적화 필요하신 분?

각 시간 단계^{time step}마다 소규모의 최적화 문제를 해결하는게 아니라, 왜 거대한 신경망이 해결책을 바로 내놓게끔 하지 않는가?

우리의 소망은 충분한 복잡도를 가진 신경망을 훈련시키는 것이다. 이는 본질적으로 한 번에 최적화 문제를 해결하고, 각 시간 단계마다 최적화 문제를 풀은 결과만큼이나 좋은 출력값을 내놓는다.

$B$는 심층 학습 모델이고, $y$는 관측된 푸리에 영역 데이터이다.

15년 전과 비교해서 요즘에는 구현하기 훨씬 쉬워졌다. 그림 9는 이 문제에 대한 심층 학습 접근법의 결과를 보여준다. 그 출력값도 실제 스캔본과 매우 비슷해서, 압축 센싱보다 훨씬 나아진 것을 알 수 있다.

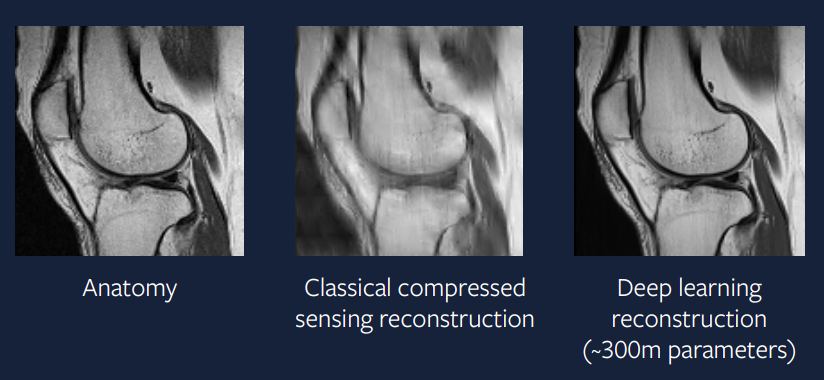
그림 9: 심층 학습 접근법

모델은 아담^ADAM과 그룹 정규화를 사용한 정규화 계층들, 유넷 기반 CNN^{U-Net based convolutional neural network}을 사용해서 재구성 이미지를 만들어냈다. 실제적인 적용 사례에 가까운 접근법이기에, 몇 년 안되어서 이런 가속화된 MRI 스캔들이 임상 실습에서 사용되는 걸 보기를 소원한다.