최적화 I

경사 하강법

이제 가장 기본이자 가장 나쁜 방법들(알고 있어야 하는)로 최적화 방법^{Optimization Methods}, 경사 하강법^{gradient descent}을 공부해보자.

문제

반복적으로 해결하는 방법^{Iterative Solution}

• 여기서 $w_{k+1}$는 $k$번째 반복^iteration이 이루어진 이후에 갱신된 값이다.
• $w_k$는 $k$번째 반복을 하기 이전의 초기값이다.
• $\gamma_k$는 이동 크기^{step size}이다.
• $\nabla f(w_k)$는 $f$의 경사^gradient이다.

여기서 함수 $f$는 연속적이고 미분가능하다고 가정한다. 우리는 최적화 함수의 최소점(골짜기)을 찾으려고 하지만, 이 골짜기의 실제 방향에 대해서는 알 수 없다. 국소적인 부분만 볼 수 있기에, 음의 경사의 방향만이 최고의 정보이다. 그 방향으로 작게 한걸음 내딛는 것이 최저점에 가까이 갈 수 있는 유일한 길인 것이다. 걸음을 딛으면 골짜기에 도달할때까지, 다시 새로운 경사를 계산하고 그 방향으로 또 조금 움직인다. 때문에, 경사 하강법은 기본적으로 가파르게 하강하는^{steepests descent}(음의 경사) 방향을 따라 이루어진다.

반복적으로 갱신하는 수식에서 $\gamma$ 매개 변수는 이동 크기^{step size}라고 한다. 일반적으로 최적의 이동 크기 값을 알 수 없기 때문에 다양한 값들을 시도하게 된다. 훈련 방법은 보통 로그 단위로 한번에 여러개의 값을 시도해본 다음, 그 중 최적값을 사용하는 것이다. 여기에는 발생 가능성이 있는 다른 시나리오들도 있다. 그림은 1D 이차방정식에 대한 이러한 시나리오를 묘사한 것이다. 학습률이 너무 낮더라도 최저점을 향해 이동하기는 하겠지만, 최선의 방법보다 더 많은 시간을 소모할 것이다. 곧바로 최저점으로 갈 수 있는 이동 크기를 찾는건 무척 어렵거나 불가능하다. 이상적인 이동 크기의 수치는 최적의 이동 수치보다 약간 크게 잡는 것이다. 실제로 이렇게 하면 가장 빠르게 수렴된다. 하지만, 만약 학습률을 너무 크게 사용할 경우, 최소점에서 계속 멀어질 것이고 발산해버릴것이다. 실제 적용시에는 학습률을 발산하지는 않을 정도의 크기로 사용한다.

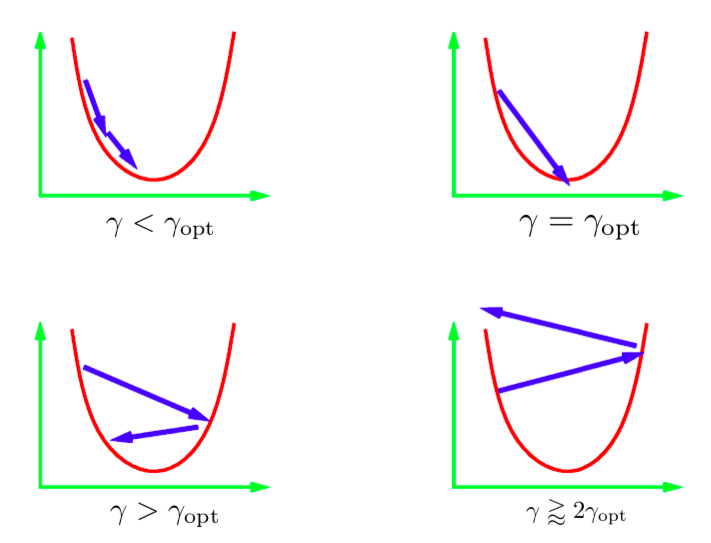
그림 1: 1차원 이차방정식에서의 이동 크기step sizes

확률적 경사 하강법

확률적 경사 하강법에서는 경사 벡터의 확률적 추정으로 실제 경사 벡터를 대체한다. 신경망에서의 확률적 추정이란, 세부적으로는 한 데이터 지점에서 손실의 경사를 의미한다.

$f_i$가 $i$번째 인스턴스에서의 네트워크 손실을 나타낸다고 하자.

결국 최소화하고자 하는 함수는 $f$이며, 모든 인스턴스들의 총 손실^{total loss}이다.

SGD에서는 $f_i$의 경사를 따라 가중치들을 갱신한다. (전체 손실 $f$의 경사와는 반대이다)

만약 $i$가 무작위로 선택된다면, $f_i$에 노이즈가 있어도 $f$의 불편 추정량^{unbiased estimator}이 될 것이고, 수학적으로는 아래와 같이 쓸 수 있다.

이 결과로 예상되는 SGD의 $k$번째 단계는 전체 경사 하강법의 $k$번째 단계와 같다.

그래서 어떤 SGD 갱신이라도 전체 배치 갱신의 기대값과 같다. 하지만, SGD는 노이즈가 있는 단순히 더 빠르기만 한 경사 하강법이 아니다. SGD는 더 빠를 뿐만 아니라, 전체 배치 경사 하강법보다 더 나은 결과물들도 내놓는다. SGD의 노이즈는 얕은 국소 최저점를 피하고, 더 나은 (더 깊은) 최저점을 찾을 수 있도록 도와준다. 이런 현상을 담금질^annealing이라고 부른다.

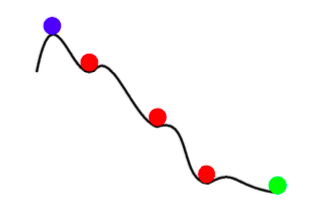
그림 2: SGD에서의 담금질

요약하자면, 확률적 경사 하강법의 이점은 아래와 같다:

1. instances에는 불필요한 정보들이 많다. SGD는 이런 불필요한 연산들이 많아지는 걸 방지한다.
2. 학습 초반, 경사 내부의 정보에 비해 노이즈는 작다. 때문에 SGD 단계는 사실상 GD 단계 만큼이나 좋다.
3. 담금질 - SGD를 갱신할 때의 노이즈는 나쁜(얕은) 국소 최저점으로의 수렴을 방지할 수 있다.
4. 확률적 경사 하강법은 계산 비용이 상당히 저렴하다 (모든 데이터 지점들을 갈 필요가 없다)

미니 배치

미니 배치에서는 하나의 인스턴스만을 계산하는 대신, 다수의 무작위로 선택된 인스턴스들의 손실을 고려하게 된다. 이는 이동 단계를 갱신할 때 노이즈를 줄인다.

우리는 종종 한 인스턴스 대신 미니 배치를 사용함으로써, 우리의 하드웨어를 더 낫게 사용할 수 있다. 한 예로, 우리가 하나의 인스턴스 훈련을 할 때 GPUs는 형편없게 활용되었다. 분산 네트워크 훈련 기법은 클러스터 기계들 사이에서 거대한 미니 배치를 나누고, 결론으로 나온 경사들^gradients을 합친다. 페이스북은 최근 분산 훈련을 사용해서, 이미지넷 데이터^{ImageNet data}를 네트워크에 한 시간내로 훈련시켰다.

기억할 필요가 있는 것은, 경사 하강법은 절대로 전체 크기의 배치로 사용해서는 않된다는 점이다. 전체 배치 크기를 트레이닝시키고 싶을 경우에는, LBFGS라고 불리는 최적화 기법을 사용하라. 파이토치^PyTorch와 사이파이^Scipy 모두 이 기법의 구현체를 제공한다.

모멘텀

모멘텀에서는 한 번이 아니라 두 번의 반복 작업($p$ 와 $w$)을 한다. 갱신은 아래처럼 된다.

$p$는 SGD 모멘텀이라고 불리운다. 갱신때마다 우리는 인자 $\beta$ (0과 1사이의 값)를 감쇠한 이후의 확률적 경사를 모멘텀의 이전 값에 더한다. $p$는 경사들의 실행 평균^{running averages}으로 생각할 수 있다. 마침내 우리는 새로운 모멘텀 $p$의 방향으로 $w$를 움직인다.

대안 형태 : 확률적 무거운 공 방법

이 형태는 이전과 수학적으로 동일하다. 이 다음 단계는 이전 단계의 방향( $w_k - w_{k-1}$)과 새로운 음의 경사의 조합이 된다.

직관

SGD 모멘텀은 물리학에서의 모멘텀 컨셉과 비슷하다. 최적화 과정은 언덕을 굴러내려가는 무거운 공과 닮아있다. 모멘텀은 공이 이미 움직이던 곳과 같은 방향으로 움직이도록 유지해준다. 경사는 어떤 다른 방향으로 공을 힘줘서 미는 것과 같다고 생각할 수 있다.

Figure 3: 모멘텀의 효과
Source: distill.pub

방향에 극적인 변화를 주려고 하기보다 (그림 왼쪽에서 보이듯이), 모멘텀은 적절한 변화를 만들어낸다.

모멘텀은 SGD만 사용할 때 자주 발생하는 진동 현상을 감쇠한다.

매개 변수 $\beta$는 감쇠 인자^{Dampening factor}로 불리운다. $\beta$는 0보다 큰 수여야 하는데, 0과 같을 경우 그냥 경사 하강법을 하는 것이 되기 때문이다. 또한 1보다 작은 수여야 하는데, 그렇지 않을 경우 (경사가) 폭발해버릴 것이기 때문이다. 더 작은 $\beta$ 값들은 방향을 더 빠르게 바꾼다. 더 큰 값일수록, 변경에 시간이 걸린다.

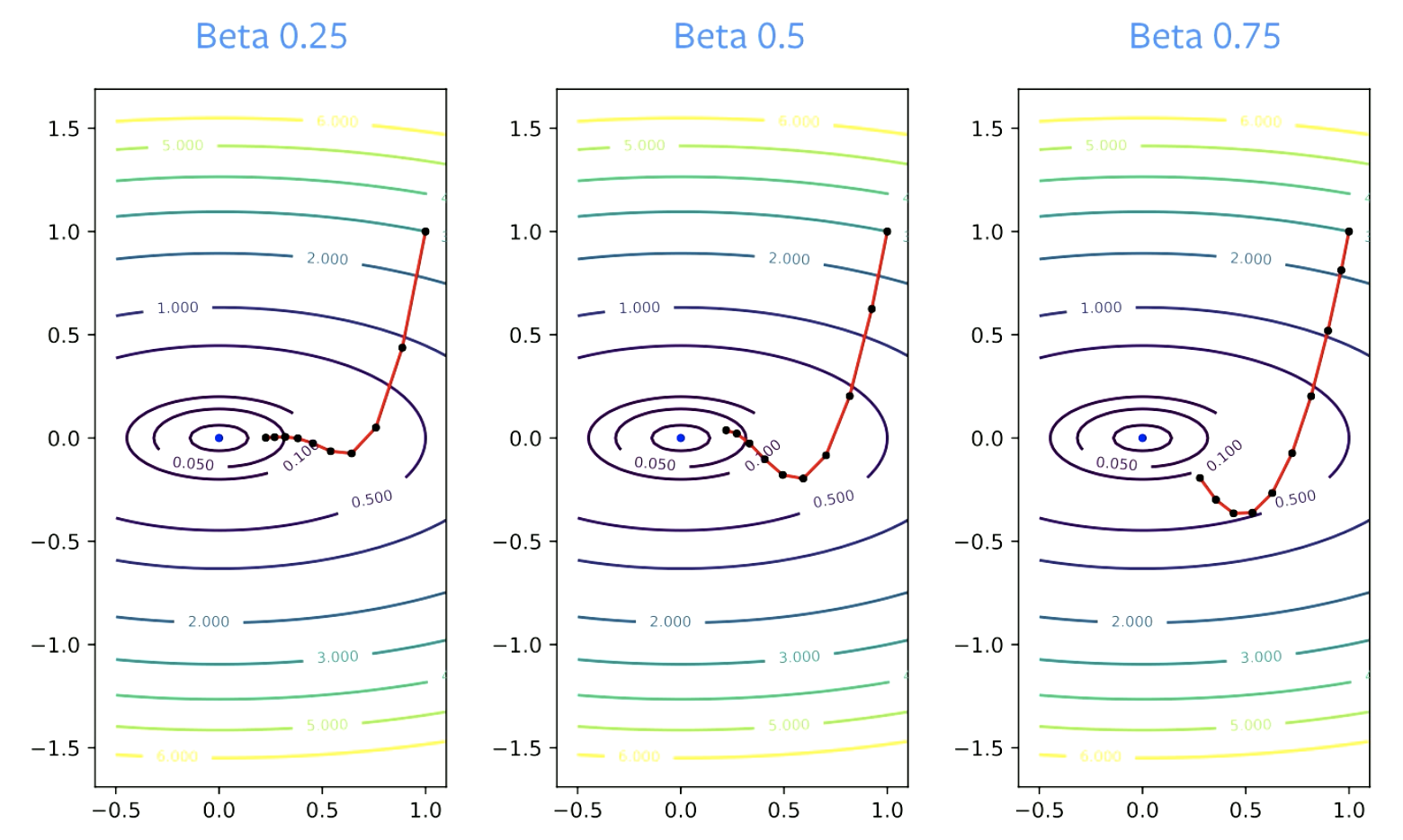
그림 4: 수렴에서 베타의 영향

실용적인 가이드라인

모멘텀은 거의 대부분 확률적 경사 하강법과 함께 쓰여야 한다. $\beta$ = 0.9 또는 0.99 거의 항상 잘 동작한다.

이동 단계^{step size} 매개변수는 모멘텀 매개변수가 증가할 때, 수렴을 유지하기 위해 종종 줄어들 필요가 있다. 만약 $\beta$가 0.9에서 0.99로 바뀐다면, 반드시 10의 인수로 감소해야한다.

왜 모멘텀이 동작할 수 있는가?

가속

아래는 네스트로프 모멘텀의 갱신 규칙^{update rule}이다.

네스트로프 모멘텀에서 조심스럽게 상수값을 선택한다면 빠르게 수렴하도록 만들 수 있다. 그러나 볼록 문제들^{convex problems}에만 적용 가능하고, 신경망에는 적용할 수 없다.

많은 이들이 표준 모멘텀이 가속 방식이기도 하다고 하지만, 실제로는 이차방정식에서만 가속된다. 또한, SGD에는 노이즈 있고 가속은 노이즈와 함께해서는 잘 동작하지 않기에, SGD에서는 가속이 잘 되지 않는다. 따라서, 약간의 가속이 모멘텀 SGD에서 나타난다 하더라도, 그 자체로는 이 방법의 좋은 성능을 잘 설명해주지 못한다.

노이즈 스무딩

아마도 왜 모멘텀이 동작하는가에 관한 더 실질적인 이유는 노이즈 스무딩^{noise smoothing}일 것이다.

모멘텀은 경사값들을 평균낸다. 이는 우리가 각 단계를 갱신하기 위해 사용하는, 경사의 이동하는 평균^{running average}이다.

이론적으로는, SGD가 동작하게끔 하기 위해 모든 단계의 갱신값들을 평균내야 한다.

모멘텀과 함께 사용하는 SGD의 대단한 점은 이 평균을 내는 작업이 더 이상 필요하지 않다는 것이다. 모멘텀은 최적화 과정에서 해결책을 위한 좋은 추정을 각기 갱신해주는 스무딩을 더해준다. SGD에서는 전체 갱신값을 평균을 내고, 그 이후에 그 방향으로 한 걸음 딛는다.

가속과 노이즈 스무딩 모두 모멘텀이 높은 성능을 내도록 도와준다.

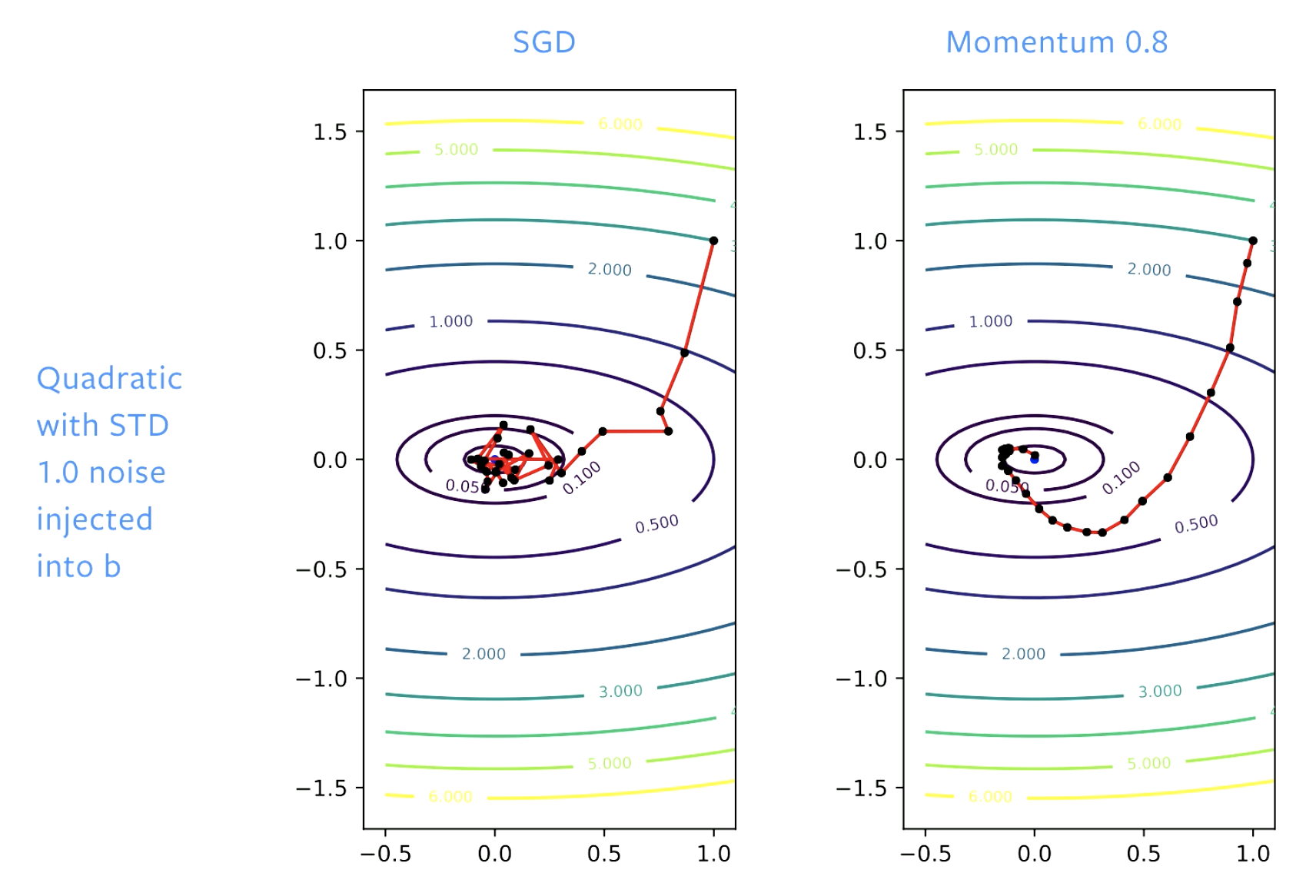
그림 5: SGD vs. 모멘텀

SGD에서 해결책들을 따라 발전이 있었지만, 경사(골짜기의 바닥)에 도달했을 때는 그 층에서 튀어오를것이다. 이를 느리게 튀어오르도록 학습률을 조정한다면 어떨까. 모멘텀으로 (학습률을) 더 부드럽게 조절한다면, 튀어오르지 않게 된다.