선형대수와 합성곱

🎙️ Alfredo Canziani

선형대수 복습

이 파트는 신경망 맥락 안에서의 기초 선형대수 개요에 관한 내용입니다. 단순 은닉층 $\boldsymbol{h}$에 대해 먼저 알아보겠습니다.

\[\boldsymbol{h} = f(\boldsymbol{z})\]

출력값은 벡터 $z$에 적용된 비선형 함수 $f$입니다. 여기서 $z$는 $\boldsymbol{x} \in\mathbb{R^n}$인 입력 벡터에 대하여 $\boldsymbol{A} \in\mathbb{R^{m\times n}}$인 아핀 변환의 출력값입니다.

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

그러므로 단순 편향값들은 무시됩니다. 이 때, 선형방정식은 다음과 같이 확장할 수 있습니다.

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

(단, $\boldsymbol{a}^{(i)}$는 행렬 $\boldsymbol{A}$의 $i$번째 행에 위치합니다.)

이 변환의 의미를 이해하기 위해서, $a^{(1)}\boldsymbol{x}$와 같은 $\boldsymbol{z}$의 한 요소를 분석해봅시다. $n=2$일 때, $\boldsymbol{a} = (a_1,a_2)$ 그리고 $\boldsymbol{x} = (x_1,x_2)$라 하겠습니다.

$\boldsymbol{a}$ 와 $\boldsymbol{x}$ 는 2차원 축으로 나타낼 수 있습니다. 이제, $\boldsymbol{a}$ 와 $\hat{\boldsymbol{\imath}}$ 사이의 각이 $\alpha$이고 $\boldsymbol{x}$ 와 $\hat{\boldsymbol{\imath}}$ 사이의 각을 $\xi$라 한다면, 삼각공식 $a^\top\boldsymbol{x}$은 아래와 같이 풀어쓸 수 있습니다.

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

출력값은 행렬 $\boldsymbol{A}$의 특정 행에 대한 입력값 정렬을 계산합니다. 우리는 이것을 두 벡터 $\xi-\alpha$ 사이의 각을 관찰함으로써 이해할 수 있습니다. $\xi = \alpha$일 때, 두 벡터는 완벽하게 정렬되고 최대값 또한 정해집니다. 만약 $\xi - \alpha = \pi$이면, $\boldsymbol{a}^\top\boldsymbol{x}$는 그것의 최소값을 가지게 되고 두 벡터는 반대 방향을 가리키게 됩니다. 본질적으로, 선형 변환은 $A$에 의해 정의된 다양한 방향에 대한 입력값의 정사영을 볼 수 있게 합니다. 이 직관은 마찬가지로 더 높은 차원으로 확장할 수 있습니다.

선형변환을 이해하기 위한 또 다른 방법은 바로 $\boldsymbol{z}$가 아래와 같이 확장가능하다는 것을 이해하는 것입니다.

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

출력값은 행렬 $\boldsymbol{A}$의 열의 가중합입니다. 그러므로 이는 아무것도 아니지만, 입력값의 구성요소입니다.

선형대수, 합성곱으로의 확장

이제 우리는 선형대수를 오디오 데이터 분석 예시를 통해 합성곱으로 넓혀볼 것입니다. 행렬곱 형태의 완전 연결 계층을 표현하는 것으로 시작합니다.

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

이번 예제에서는 가중 행렬은 $4 \times 3$, 입력 벡터는 $3 \times 1$ 그리고 출력 벡터는 $4 \times 1$임을 보여주고 있습니다.

그러나 오디오 데이터는 훨씬 더 긴 편입니다. (3-샘플 길이가 아님) 오디오 데이터에서 샘플 수는 오디오 길이(예, 3초)와 샘플레이트(예, 22.05kHz)의 곱과 같습니다. 아래에서 보여주고 있듯이,입력 벡터 $\boldsymbol{x}$는 꽤 길 것입니다. 그만큼, 가중 행렬은 커질 것입니다.

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

위 공식은 학습하기 어려울 것입니다. 하지만 다행히도 단순하게 만들 방법이 있습니다.

특성: 국소성

데이터의 국소성으로 인하여 (관계 없는 데이터는 신경쓰지 않기로 합니다.) 위 가중 행렬의 $w_{1k}$은 $k$가 상대적으로 클 때 0으로 채워질 수 있습니다. 그러므로 행렬의 첫 번째 행은 사이즈가 3인 커널이 됩니다. 이 3-사이즈 커널을 $\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$로 나타내봅시다.

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

특성: 정상성

자연적인 데이터 신호는 정상성을 가집니다.(즉, 확실한 패턴/모티프는 반복합니다.) 이는 우리가 이전에 정의했던 $\mathbf{a}^{(1)}$ 커널을 다시 쓸 수 있게 도와줍니다. 우리는 매번 각 단계마다(즉, stride는 1) 그것을 둠으로써 이 커널을 사용하고, 동시에 다음과 같은 결과를 얻게 됩니다.:

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

행렬의 오른쪽 윗 부분과 아랫쪽 왼쪽 부분 모두 국소성 덕분에 0으로 채워지고, 희소성이 생겼습니다. 확실한 커널을 반복해서 재사용하는 것을 가중치 공유라 부릅니다.

Multiple layers of Toeplitz matrix 토플리츠 행렬의 다중 층위

이러한 변화 이후, 남은 매개 변수 수는 3($a_1,a_2,a_3$)입니다. 앞서 매개 변수 값이 12($w_{11},w_{12},\cdots,w_{43}$)였던 가중 행렬과 비교했을 때, 현재 매개 변수 수는 매우 제한적이며 우리는 이것을 확장하고자 합니다.

이전 행렬은 $\boldsymbol{a}^{(1)}$ 커널을 동반한 층위(합성곱 층위)로 여겨질 수 있습니다. 그러면 우리는 매개 변수를 늘림으로써 $\boldsymbol{a}^{(2)}$, $\boldsymbol{a}^{(3)}$와 같은 다른 커널을 이용하여 다중 층위를 만들 수 있습니다.

각 층위는 여러번 복제된 단 하나의 커널을 포함하는 행렬을 가집니다. 이 유형을 토플리츠 행렬^{Toeplitz matrix} 이라 부릅니다. 모든 토플리츠 행렬에서, 왼쪽에서 오른쪽으로 내려가는 대각선(주대각선)은 상수입니다. 또한, 우리가 여기서 사용하는 토플리츠 행렬들은 희소 행렬들입니다.

첫번째 커널 $\boldsymbol{a}^{(1)}$와 입력 벡터 $\boldsymbol{x}$가 주어졌을 때, 이 층위에 의해 주어진 출력값에서의 첫번째 입력은 $a_1^{(1)} x_1 + a_2^{(1)} x_2 + a_3^{(1)}x_3$입니다. 그러므로 모든 출력 벡터는 다음과 같습니다.

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

비슷한 결과를 얻기 위해 동일 행렬을 복제하는 방법은 이어지는 $\boldsymbol{a}^{(2)}$, $\boldsymbol{a}^{(3)}$와 같은 다른 커널을 동반한 합성곱 층위에 적용될 수 있습니다.

합성곱 듣기 - 주피터 노트북

(https://github.com/Atcold/pytorch-Deep-Learning/blob/master/07-listening_to_kernels.ipynb).

주피터 노트북에서 작성된 내용은 여기서 확인할 수 있습니다.

이 노트북에서 우리는 ‘스칼라 곱 실행’으로서의 합성곱에 대해 알아볼 것입니다.

librosa 라이브러리는 오디오 클립 $\boldsymbol{x}$를 불러올 수 있게 해주며, 샘플링 속도입니다. 이 때, 70641개의 샘플이 있으며, 샘플링 속도는 22.05kHz이고 클립의 총 길이는 3.2초입니다. 불러온 오디오 신호는 웨이브 형태를 띄며(그림1 참조), 우리는 마치 $y$축 진폭으로부터 들리는 것 같은 소리가 무엇인지 알아낼 수 있습니다. 사실, 오디오 신호 $x(t)$는 윈도우 종료 시 재생되는 소리입니다.(그림2 참조)

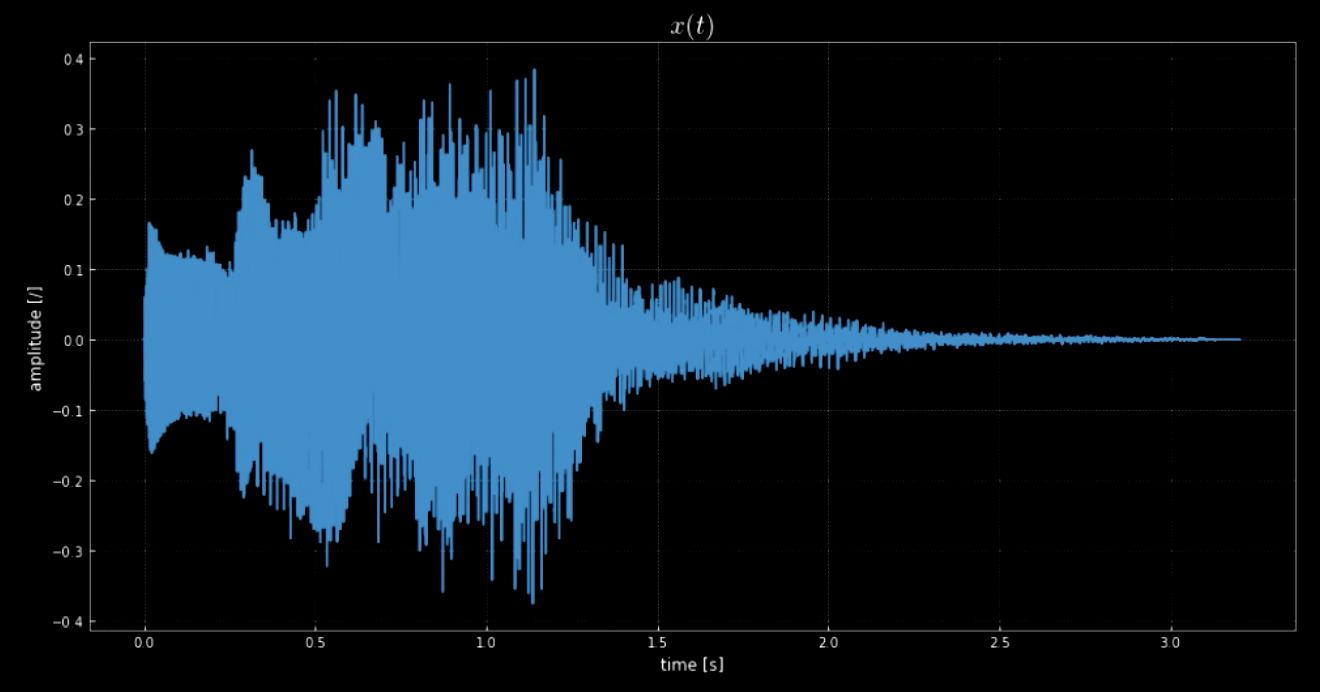
그림 1: 오디오 신호 시각화

그림 2: 위 오디오 신호에 대한 음표.

우리는 파동형태로부터 음표들을 분리해야 합니다. 이를 위하여, 우리가 푸리에 변환(FT)을 사용한다면 모든 음표들이 한꺼번에 나올 것이고, 정확한 시간과 각 피치의 위치를 알아내기 어려울 것입니다. 그러므로, 스펙트로그램이라 알려진 국지적 푸리에 변환(스펙트로그램)이 필요합니다. 스펙트로그램에서 관찰됨으로써(그림 3 참조), 다른 피치들은 다른 주파수(예, 첫 번째 피치는 1600에서 정점을 찍습니다.)에서 정점을 찍습니다. 그들 주파수에서 네 개의 피치를 연결하는 것은 원래 신호의 피치된 버전을 우리에게 주게 됩니다.

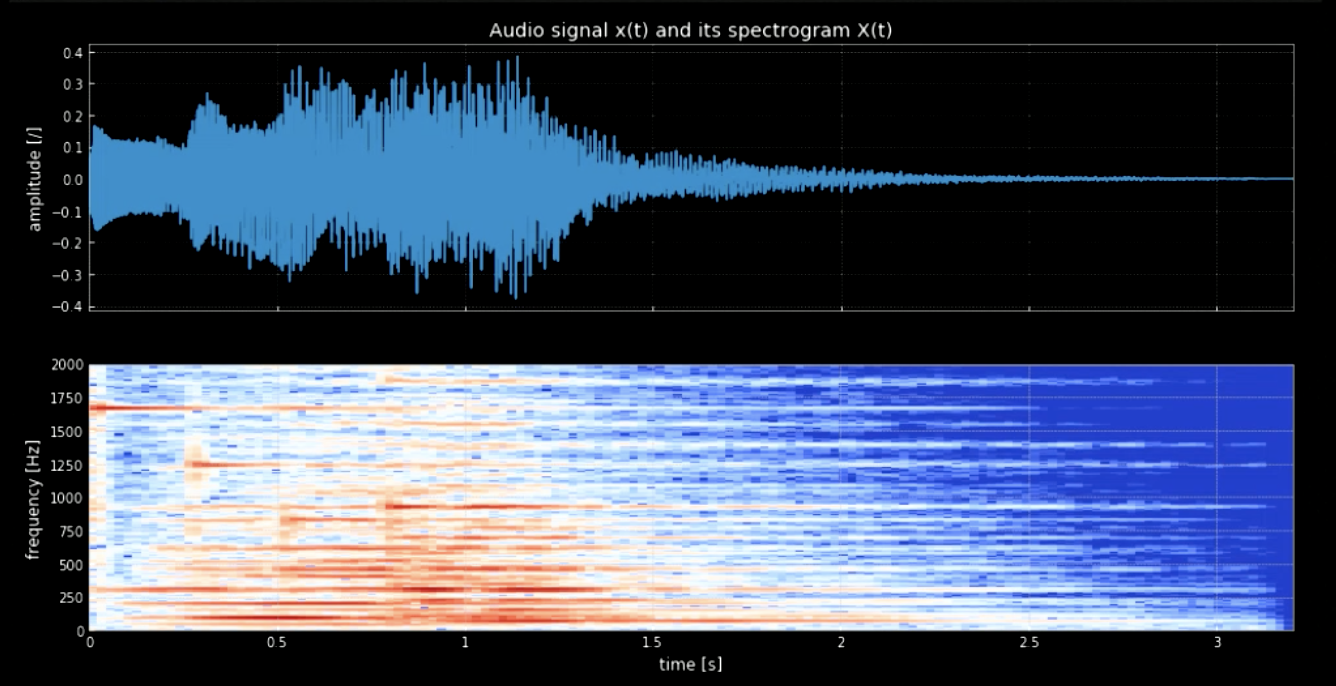
그림 3: 오디오 신호와 스펙트로그램.

모든 피치(예를 들면 피아노의 모든 키)를 동반한 입력 신호의 합성곱은 입력 조각에 있는 모든 노트(오디오가 특정 커널과 맞을 때 히트)를 추출할 수 있도록 도와줍니다. 본래 신호의 스펙트로그램과 연결된 피치의 신호는 그림4와 같이 나타나는 반면, 본래 신호의 주파수와 네 피치는 그림 5와 같이 나타납니다. 입력 신호(본래 신호)를 동반한 네 커널의 합성곱 플롯은 그림 6에서 볼 수 있습니다. 합성곱의 오디오 클립과 마찬가지로 그림 6은 노트 추출에서 합성곱의 효율성을 보여주고 있습니다.

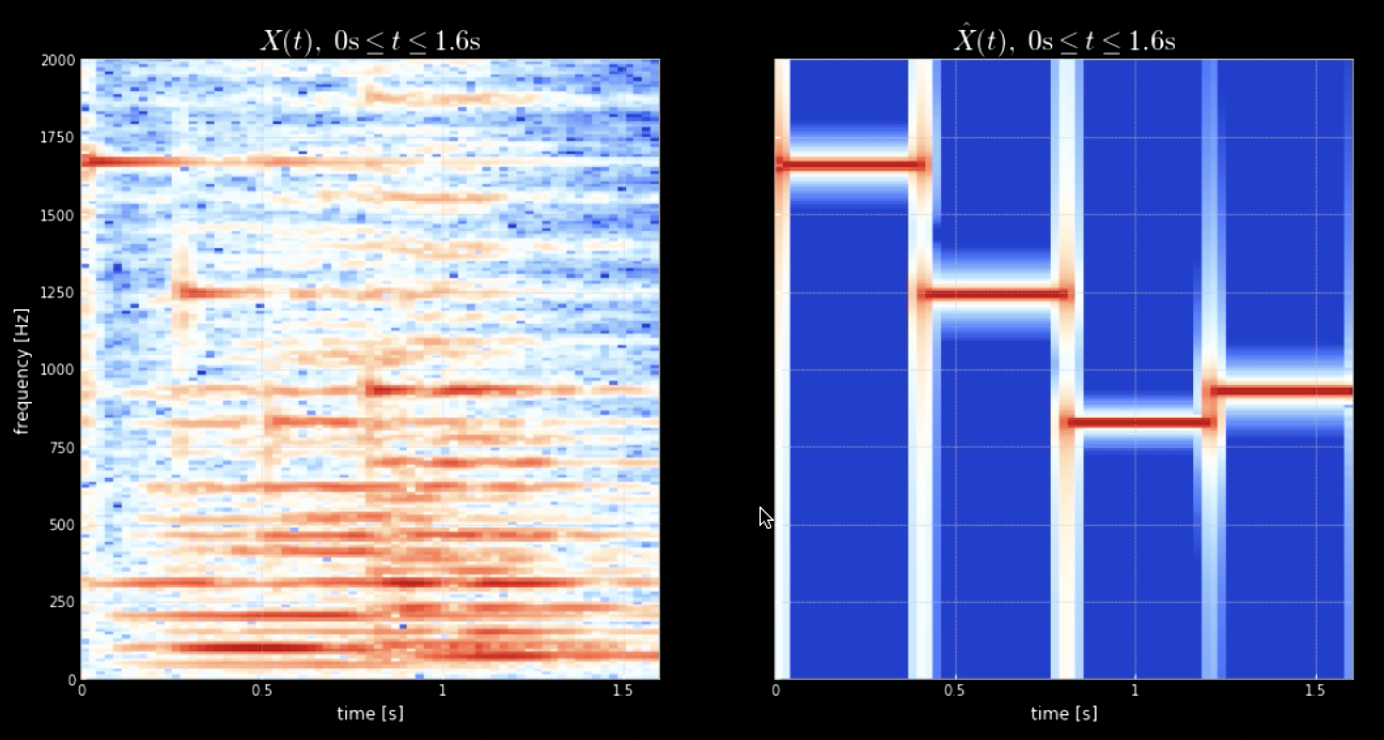
그림 4: 원래 신호 스펙트로그램(왼쪽)과 피치 연결 스펙트로그램(오른쪽).

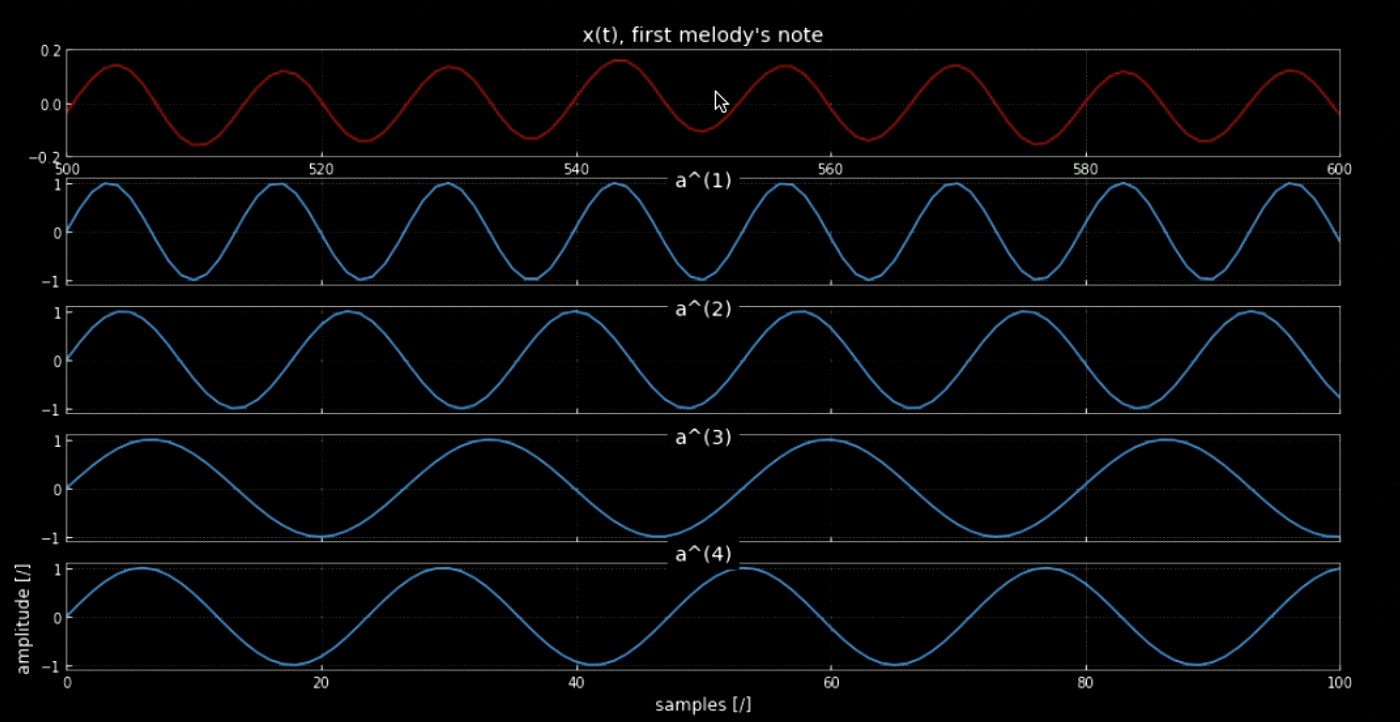
그림 5: 첫번째 멜로디 음표.

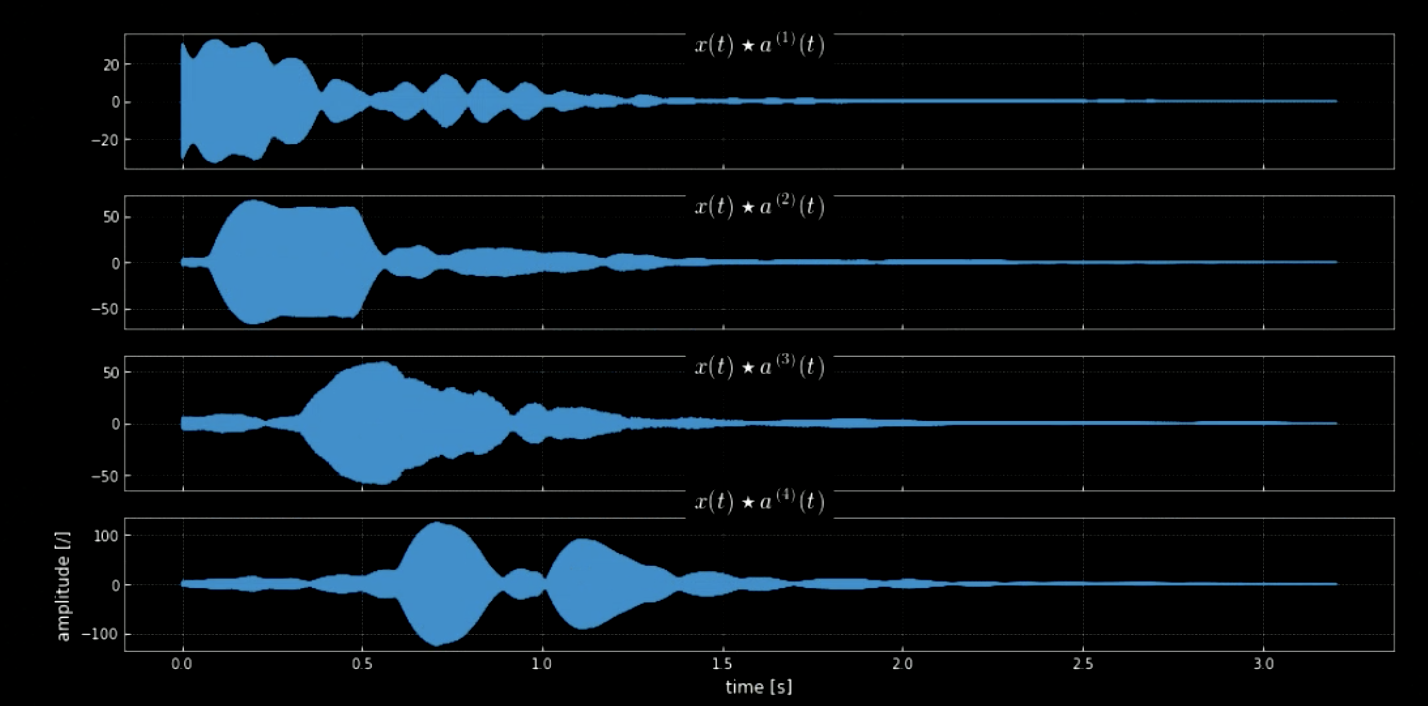
그림 6: 네 커널의 합성곱.

다른 데이터셋의 차원수

마지막 파트는 차원수의 다른 표현에 대한 여담과 동일한 부분을 다룬 예제에 관한 내용입니다. 여기서 우리가 고려할 입력 세트 $X$는 $\Omega$ 도메인부터 채널 $c$까지 맵핑하는 함수로 만들어져 있습니다.

예제

• 오디오 데이터: 1-D 도메인, 시간에 따라 구분된 신호; 채널수 범위는 1(모노), 2(스테레오), 5+1(돌비 5.1) 등입니다.
• 이미지 데이터: 2-D 도메인(픽셀); $c$의 범위는 1(회색톤), 3(컬러), 20(초분광) 등입니다.
• 특수 상대성: 도메인은 $\mathbb{R^4} \times \mathbb{R^4}$ (시공간 $\times$ 사차원 운동량); $c=1$일 때, 해밀턴이라 부릅니다.

그림 7: 다른 타입을 가지는 신호의 다른 차원

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
ChoongHee Lee
18 Feb 2020