자연신호의 특징

자연신호의 성질

모든 신호는 하나의 벡터로 생각할 수 있다. 예를 들어, 오디오 신호는 1차원 신호로 $x_t$가 각 시간 $t$에서의 파형의 진폭으로 표현하는 하나의 벡터 $\boldsymbol{x} = [x_1, x_2,…,x_T]$ 로 해석 가능한데, 조금 더 풀어 해석하자면, 공기의 진동을 귓속 달팽이관이 받아 하나의 신호로 바꿔 뇌로 보내고 달팽이관으로 부터 받은 신호를 뇌가 언어 모델을 이용해 언어로 바꾸게 되는 것이다 (주어진 신호에 가장 개연성이 높은 발언을 고르게 되는 것). 음악같은 경우, 신호는 복수의 채널로 이루어진 입체음향으로 사람들에게 소리가 여러 방향에서 오는 것과 같은 착각을 주기도 한다. 음악은 두 개의 채널을 가지고 있음에도 1차원 신호인데, 그 이유는 시간만이 신호가 바뀜에 영향을 받는 유일한 변수이기 때문이다.

사진과 영상들은 2차원 신호인데 그 이유는 사진정보가 곧 공간적으로 표현되기 때문이다. 각각의 픽셀이 하나의 벡터가 될 수 있음을 유의하자. 이 말인즉슨, 한 사진에 임의 수 $d$ 만큼의 채널이 있다고 가정하고 그 사진 안의 각 공간점은 $d$차원 벡터를 나타낸다. 컬러사진 경우에는 RGB 평면을 갖고 있어 차원의 수는 3이 되는데, 이 컬러사진 내의 모든점 $x_{i,j}$은 적, 녹, 청색들의 각 강도를 나타낸다.

언어 또한 위에서 보여주었던 방식으로 접근이 가능하다. 우리의 어휘 체계 안에 존재하는 각 단어는 특정한 위치의 값만 1, 나머지 값은 모두 0인 원-핫벡터^{one-hot vector}로 대응될 수 있다. 즉, 각 단어는 우리의 어휘 체계 규모 만큼의 차원을 가진 벡터이다.

자연 자료 신호는 다음과 같은 특성을 가진다:

1. 정상성^Stationarity
   • 특정 주제가 신호에 반복적으로 나타남을 뜻한다. 오디오 신호 같은 경우는, 주어진 시간범위 안에 같은 타입의 패턴이 계속 관찰되는 현상을 예로 들 수 있다. 사진의 경우 같은 시각적 패턴이 차원을 따라 계속 반복되는 현상이다.
2. 집약성^Locality
   • 가까운 포인트들끼리는 거리가 비교적 더 먼 곳에 있는 포인트보다 더 연관성을 띰. 1차원 신호의 경우, 집약성은 $t_i$에 위치한 한 임의에 고점 $x_{t_i}$와 그 고점의 근방은 비슷한 값을 가지며, $t_i$와 먼곳에 떨어진 $t_j$에 위치한 $x_{t_j}$에는 영향력이 미미함을 뜻한다. 좀 더 자세하게는, 한 신호와 다른 반전된 신호가 완벽히 겹쳐지게 된다면 그 두 신호의 컨벌루션(합성곱)은 최곳값을 갖는다. 두 개의 1차원 신호들의 합성곱(상호상관^{cross-correlation})은 두 신호의 내적^{dot product}이며, 두 벡터가 얼마나 비슷한지 혹은 가까운지를 측정하는 하나의 측정법이다. 그 말인 즉 슨, 정보는 신호의 특정한 구간과 부분에 들어있는 것이며, 사진의 경우, 한 이미지의 두 점 간의 상관도는 두 점이 더욱이 멀리 떨어질수록 낮아지는 것이다. 예로, 한 이미지의 $x_{0,0}$ 픽셀이 파란색이면, $x_{0,0}$ 근방의 픽셀들의 색이 파란색일 확률은 매우 높으며, $x_{0,0}$픽셀과 멀어지면 멀어질수록 $x_{0,0}$의 색값과 독립성을 띤다.
3. 합성성^{Compositionality}
   • 자연의 모든 것은 다른 하위 개체들로 이루어져 있다. 하나의 예시로, 문자열들의 글자들은 모여 단어를 형성하고, 그 단어들은 문장들을 만들며, 그 문장들은 모여 문서들을 만든다. 합성성의 특징은 현 세계를 설명할 수 있게 해준다.

가진 데이터가 정상성, 집약성, 합성성을 띤다면, 이용한 신경망을 바탕으로 이 성질(정상성, 집약성, 합성성)을 활용 할 수 있다.

불변^invariance과 등변^equivariance을 위한 자연 신호의 성질 활용하기

집약성 $\Rightarrow$ 희소성

Fig.1 은 5중 계층의 완전 연결망^{fully connected network}을 보여준다. 각 화살표는 입력값들과 곱해질 가중치를 나타내며, 보이는 것과 같이 위 신경망은 계산 비용이 많이 들어간다.

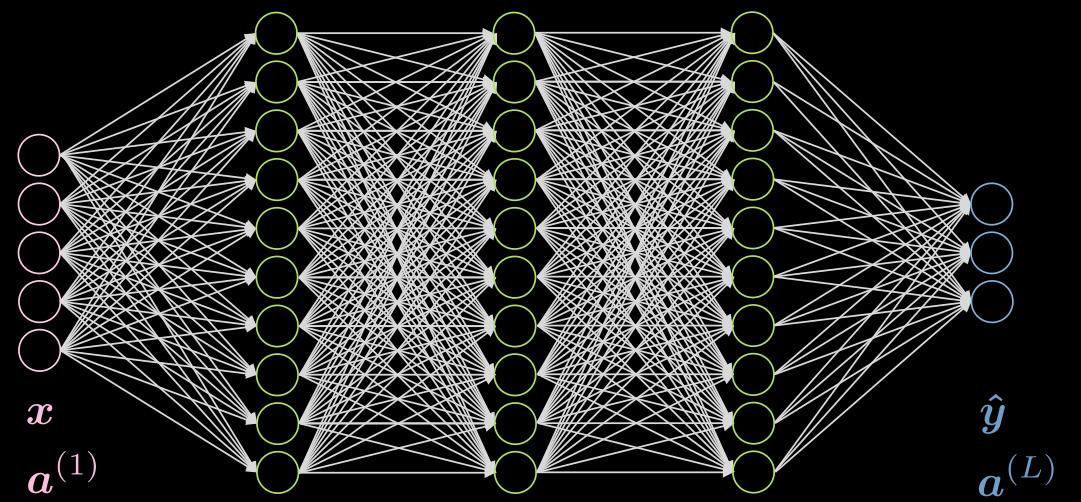
Figure 1: 완전연결 신경망

가진 데이터가 집약성을 띤다면, 각 뉴런은 전 레이어들의 소수의 로컬 뉴런에만 연결되어야한다. 그러므로, 일부 연결들은 Fig.2(b)에서 보이는 것처럼 떨어져 나갈 수 있다. (Fig.2(a)는 완전연결 신경망 FC network를 설명함). 이러한 집약성 특성의 장점을 이용해 거리가 먼 뉴런들과의 연결들을 끊을수 있고, Fig.2(b)의 히든 레이어 뉴런들은 모든 입력값을 생성^span하지는 않지만, 전반적인 구조는 모든 입력 뉴런들을 설명할 수 있다. 수용역역^{RF(receptive field)}은 특정 레이어의 각 뉴런에 영향을 미치는 전 레이어의 뉴런 수이다. 그러므로, 히든 레이어에 의한 출력 레이어의 수용역역은 $3$이고, 입력 레이어에 의한 히든 레이어의 수용역역은 $5$이다.

Figure 2(a): 희소성 적용 전	Figure 2(b): 희소성 적용 후

정상성 $\Rightarrow$ 매겨변수 공유^{parameters sharing}

데이터가 정상성의 특징을 띄운다면, 연결망 구조에 걸쳐 작은 매개변수집합을 여러번 사용할 수 있다. 예를들어, Fig.3(a)에서의 희소연결망^{sparse network}에서는 3개의 공유매개변수(노랑, 주황, 빨강)를 사용가능하며, 그로인해 매개변수의 수는 9에서 3으로 줄어들게 된다! 더욱이, 새로운 신경망 구조는 특정 가중치들을 학습시킬 데이터가 더욱 많기 때문에 더 나은 결과를 가져올수도 있을 것이다. 이러한 희소성과 매개변수 공유성을 적용시킨 위와 같은 가중치들을 합성곱 커널^{convolution kernel}이라고 부른다.

Figure 3(a): 매개변수 공유를 적용시키기 전	Figure 3(b): 매개변수 공유를 적용시키기 후

희소성과 매개변수 공유의 장점들을 나열하자면 아래와 같다:

매개변수 공유: - 더 빠른 수렴 - 더 나은 일반화 - 입력값 크기에 구애받지 않음 - 커널 독립성 -> 높은 병력화

연결 희소성: - 계산량 감소

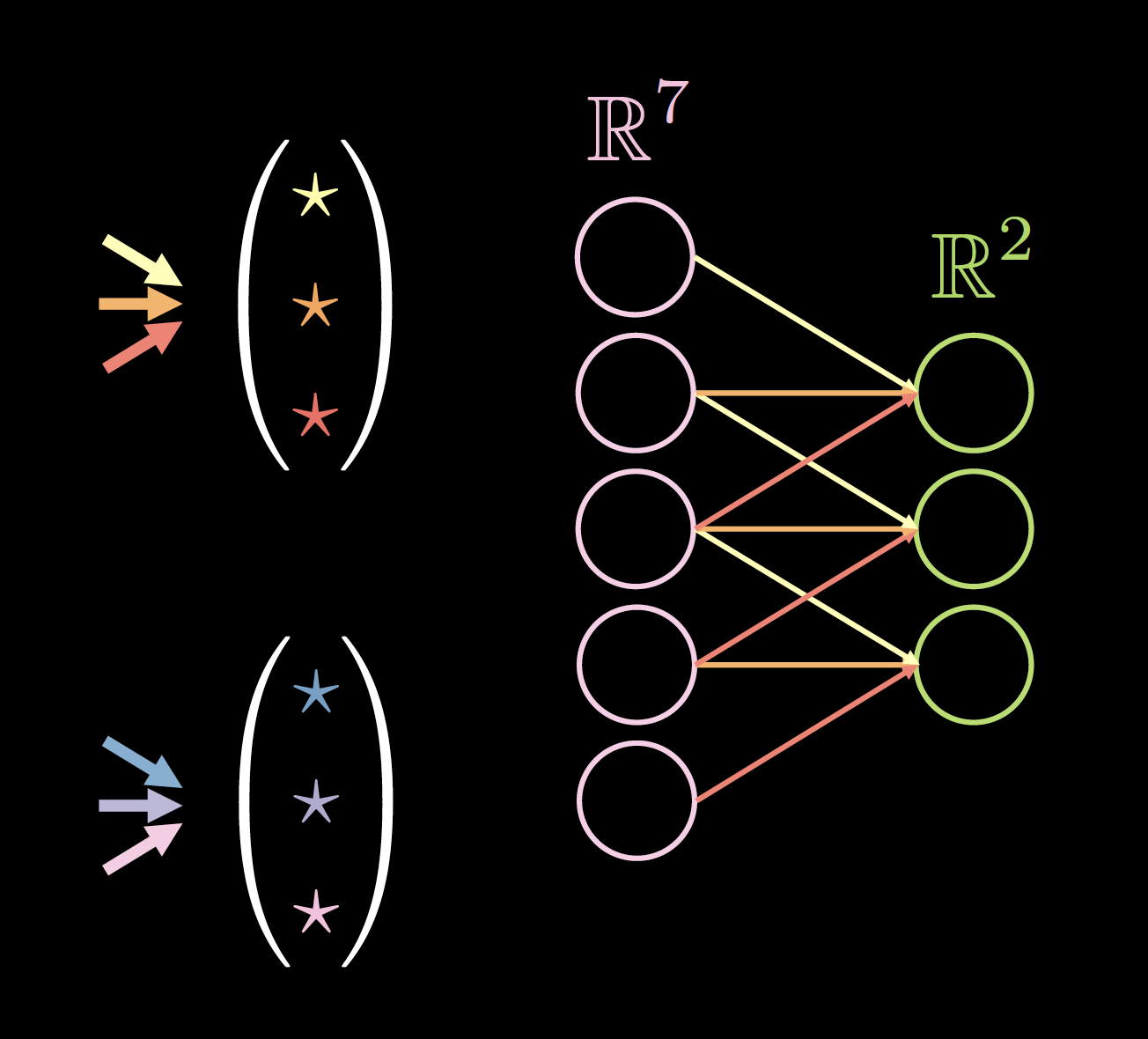
Fig.4는 사이즈가 2(커널 수), 7(전 레이어의 두께), 3(고유 연결/가중치의 수)인 1차원 데이터 커널의 한 예이다.

커널 사이즈 선택은 실증적으로 유추해낼 수 있다. 예로, 3 * 3 합성곱은 공간데이터의 최소크기로 보이지만, 크기가 1인 합성곱은 더 큰 입력 사진에 적용가능한 마지막 레이어를 얻기 위해 사용될 수 있고, 짝수의 커널 사이즈는 데이터의 질을 떨어뜨릴 수 있으므로, 커널 사이즈는 항상 3과 5같은 홀수로만 이루어진다.

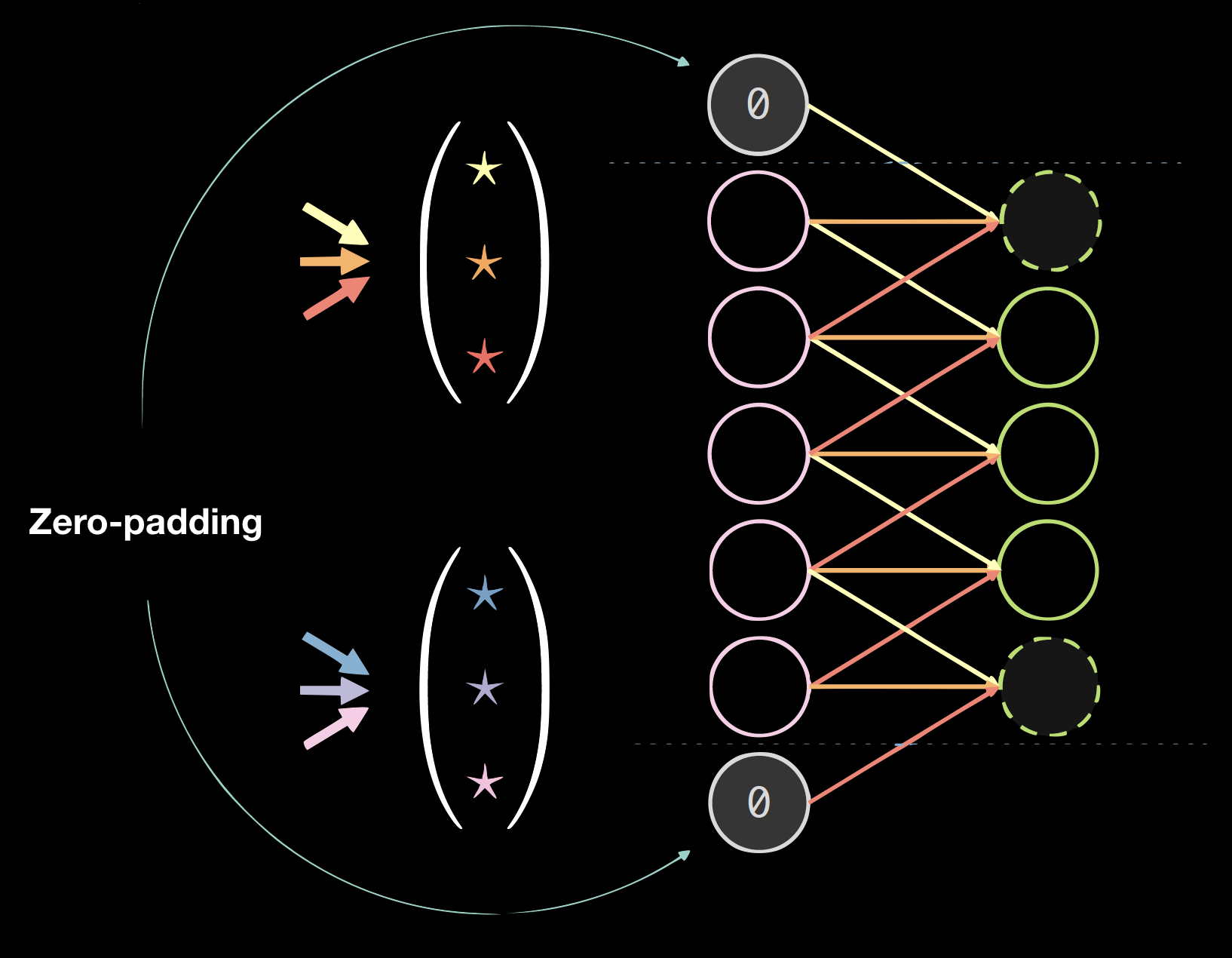Figure 4(a): 1차원 데이터의 커널	Figure 4(b):제로패딩 데이터

패딩^Padding

패딩은 전반적으로 최종 결과물의 질을 떨어뜨리지만, 프로그래밍적으로는 편리한 방법이다. 보통은 제로패딩^zero-padding을 이용하는데 계산법은 아래와 같다 사이즈 = (커널 사이즈 - 1)/2

일반적인 공간 CNN ^{standard spatial CNN}

일반적인 공간 CNN은 다음과 같은 특징을 갖고있다:

• 다중 레이어
  • 합성곱
  • 비선형성 (ReLU와 Leaky)
  • 풀링
  • 배치정규화
• 잔차 우회 연결^{Residual bypass connection}

배치 정규화와 잔차 우회연결은 연결망을 학습시키는데 정말 많은 도움이 된다.레이어가 너무 많이 쌓여 있는 경우 신호의 일부가 소실될 수 있기 때문에, 추가적인 잔차 우회로를 통해 이러한 신호가 밑에서부터 위까지 전달될 수 있는 통로와, 위에서부터 밑으로 경사값^gradients이 전달될 수 있는 경로를 확보한다.

Fig.5를 보면, (각 픽셀의 색과 같은 특징정보를 별개로) 입력 사진이 2개의 차원에 걸쳐 대부분의 공간정보^{spatial information}를 가지고 있지만, 출력 레이어는 굵다. 중간 과정을 거치며, 공간정보와 특징정보^{characteristic information}간의 트레이드 오프가 존재하며 표현은 점점 밀집되어 가며, 계층을 올라갈 수록, 공간정보를 잃음으로서 조금 더 높은 밀집표현^{dense representation}을 갖게된다.

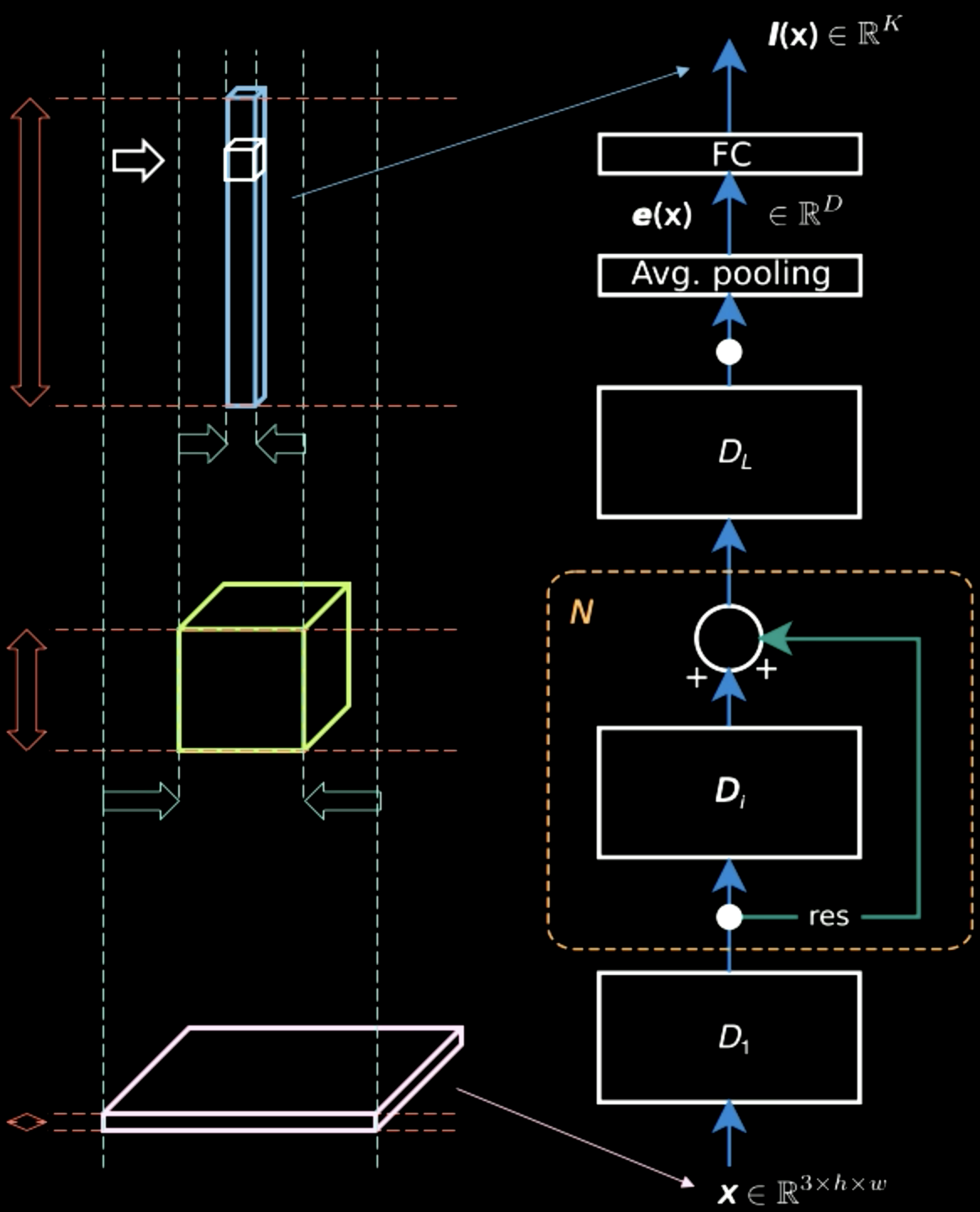
Figure 5: 계층을 올라가는 정보표현

풀링

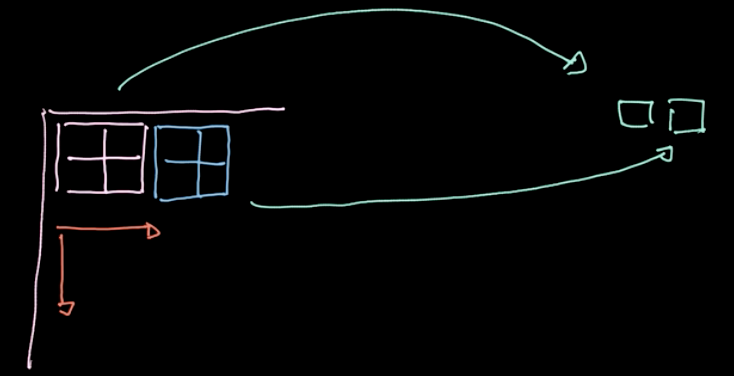
Figure 6: 풀링의 예시

$L_p$-놈^norm 이라는 연산은 다양한 지역에 적용된다(Fig.6 참조). (책의 예시는 4개의 픽셀에 하나의 값), 전체 데이터에 대해 미리 정해둔 간격^stride에 따라 이동하며 구역별로 이 연산을 반복한다.

예시로 만일 $c$개의 채널을 가진 $m * n$ 데이터를 이용한다면, 결과로 $c$개의 채널수를 유지한 $\frac{m}{2} * \frac{n}{2}$ 데이터를 얻게된다 (Fig.7). 풀링은 매개변수화 되지는 않지만, 맥스풀링^{max pooling}, 평균풀링^{average pooling} 등 여러가지의 풀링 타입을 정할 수 있고, 풀링을 사용하는 주된 목적은 데이터의 양을 줄임으로써 합리적인 계산시간을 갖기 위해서다.

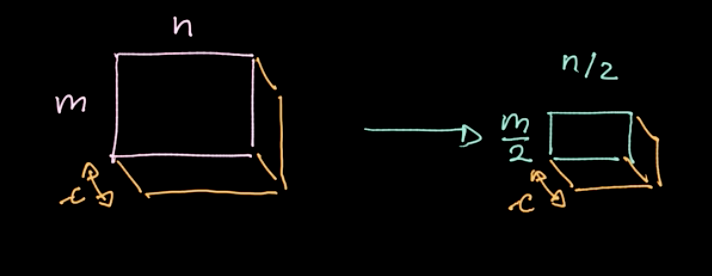
Figure 7: 풀링 결과

CNN - 주피터 노트북

위 주피터 노트북은 이 링크 에서 확인 가능. 이 주피터 노트북을 실행하기 위해서는 README.md 에서 명시된 대로 pDL 환경을 갖추었는지 확인해야 한다.

위 노트북은 MNIST 데이터셋의 분류작업을 위해 다층 퍼셉트론(완전연결 신경망)과 합성곱 신경망(CNN)을 학습시킨다. 두 신경망은 같은 수의 매개변수를 가지고 있다(Fig.8).

Figure 8: 오리지널 MNIST 데이터셋의 인스턴스

학습시키기에 앞서서, 우리는 데이터를 정규화하여 신경망의 초기 설정이 우리의 데이터 분포와 일치하도록 한다 (매우 중요!).

또한, 아래의 5가지 작업/단계가 학습 과정에 포함되었는지 확인해야 한다:

1. 모델에 데이터 전송
2. 손실 계산
3. 축적된 zero_grad() 경사도 캐시 제거
4. 경사도 계산
5. 최적화 방법을 이용한 연산 수행

첫째로, 두 신경망을 정규화된 MNIST 데이터에 학습시켰고, 그 결과, 완전 연결 신경망은 87%의 정확도를, CNN은 95%의 정확도를 보였다주어진 매개변수의 수가 두 네트워크에서 동일함을 고려했을 때, CNN이 더 많은 필터를 학습시킬 수 있었다. 완전 연결 신경망에서는 서로 멀리 떨어져 있는 픽셀 값 사이의 의존성을 파악하는 필터 학습에 쓸모없는 훈련을 진행한 반면, 합성곱 신경망 같은 경우에는, 모든 매개변수가 근접한 픽셀 간의 관계를 찾는 작업에 집중했음을 찾아볼 수 있다.

다음으로, MNIST 데이터셋의 모든 이미지의 모든 픽셀을 랜덤으로 재배열 ^{random permutation} 하였고, 이는 Fig.8을 Fig.9로 변형시키는 것과 같다. 그 후, 위의 두 신경망을 이 변형된 데이터셋에 대해 학습시켰다.

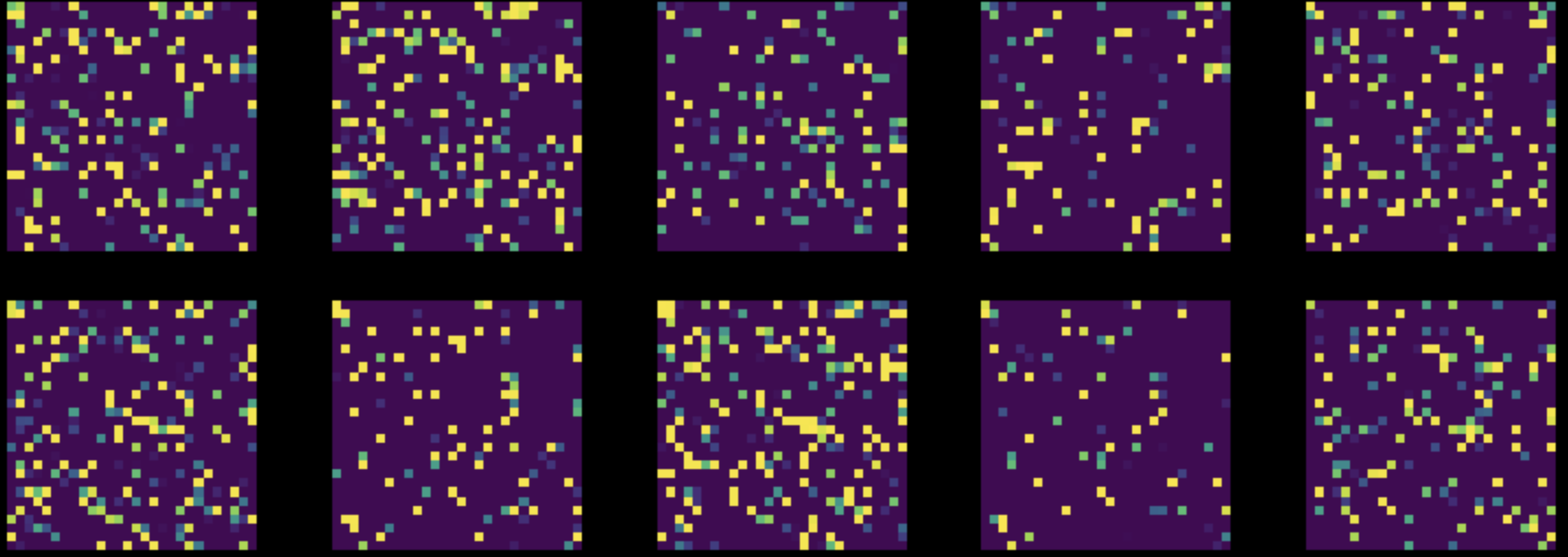
Figure 9: 재배열된 MNIST 데이터셋의 인스턴스

완전 연결 신경망의 성능은 거의 변화가 없었으나 $85$%, CNN의 정확도는 $83$%로 떨어졌다.이는, 랜덤 재배열 이후, 이미지들이 더 이상 CNN에서 활용될 수 있는 집약성, 정상성, 그리고 합성성의 특징을 보유하고 있지 않기 때문이다.