인공신경망^{Artificial neural networks (ANNs)}

🎙️ Alfredo Canziani

분류를 위한 지도 학습

• 아래의 그림 Fig. 1(a) 을 참고하자. 이 그래프의 점은 나선형의 가지에 있으며, $\R^2$ 에 위치한다. 각각의 색상은 클래스의 레이블을 나타낸다. 각기 다른 클래스의 갯수는 $K = 3$ 이다. 이는 수식으로 Eqn. 1(a) 와 같이 표현된다.

• Fig. 1(b) 은 가우시안 노이즈^noise 항이 추가된 비슷한 나선형을 보여준다. 이는 수식으로 Eqn. 1(b) 와 같이 표현된다.

  이 두 경우 모두, 나선을 이루는 점들은 선형 분류가 어렵다.

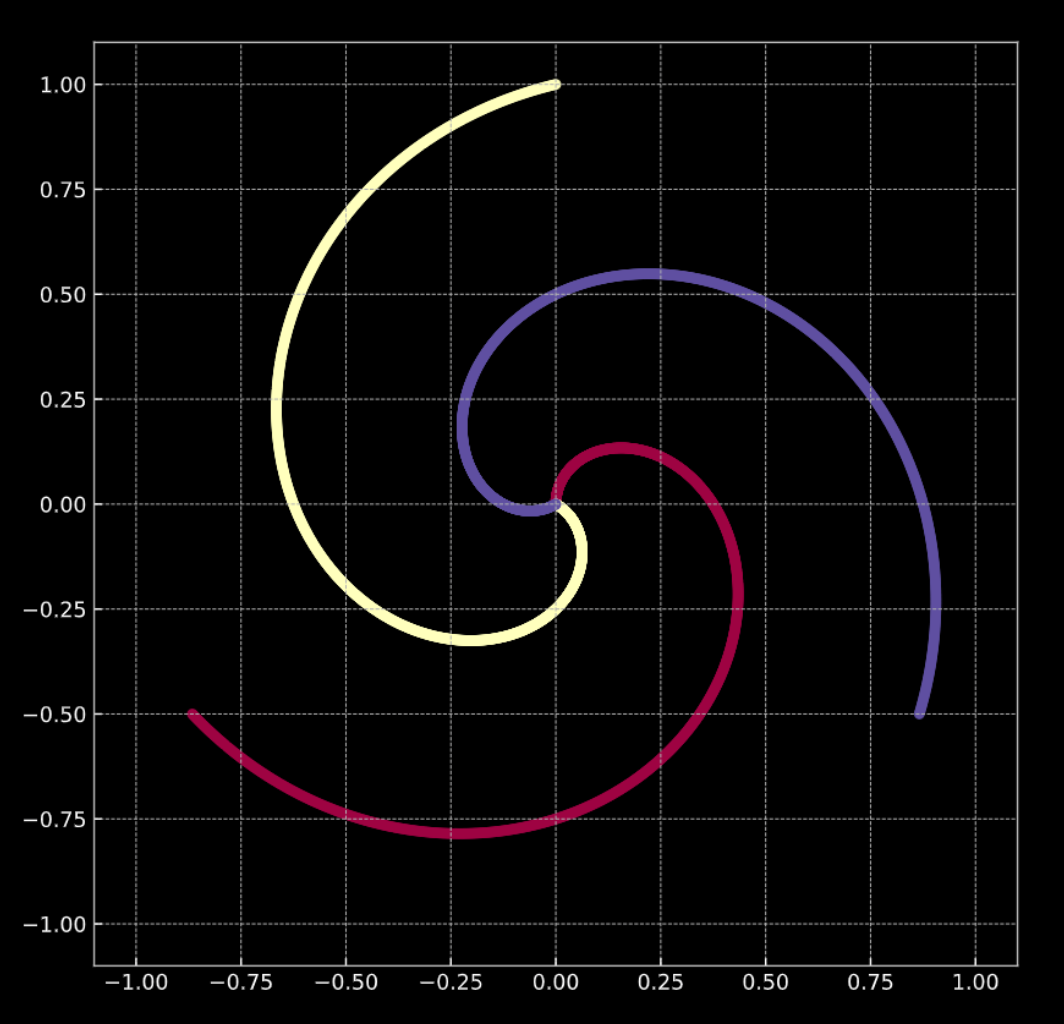
  Fig. 1(a) "노이즈가 없는" 2D 나선형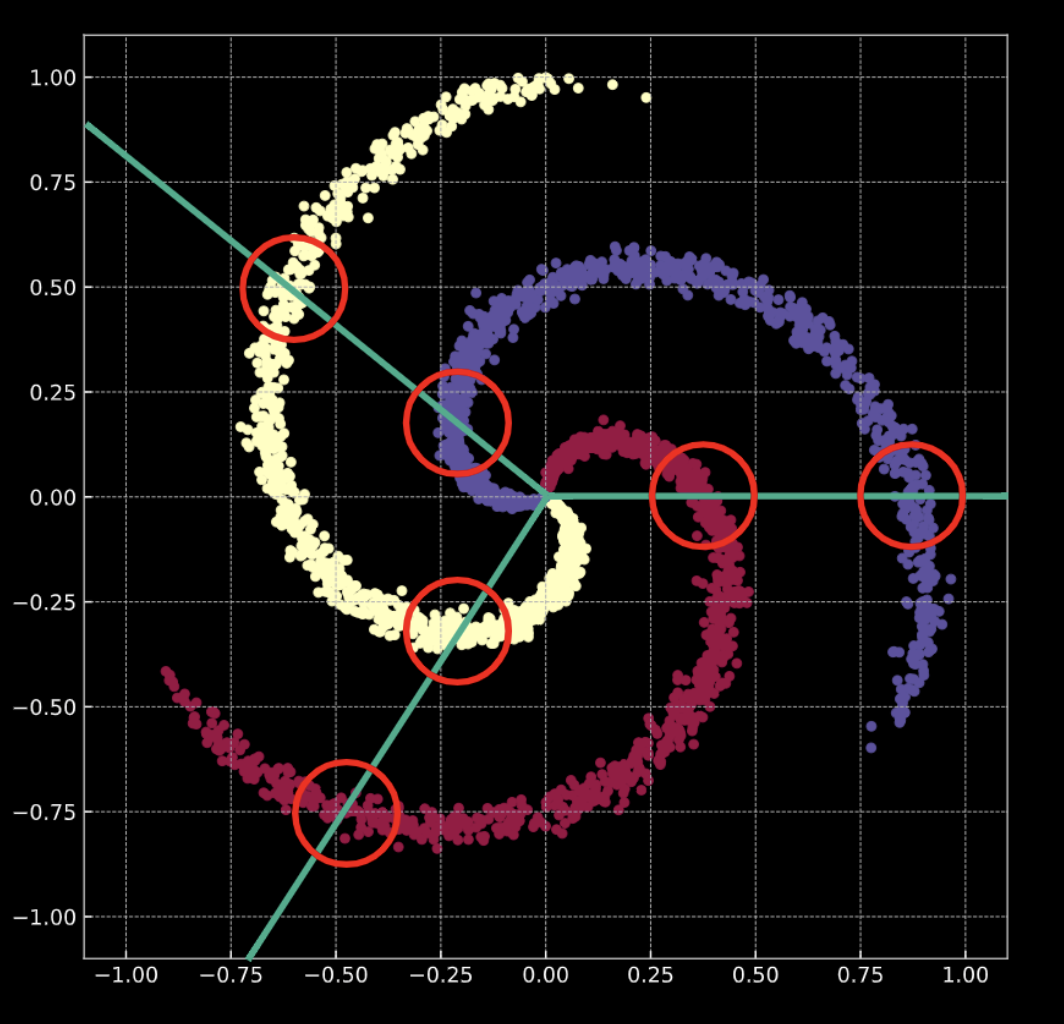

  Fig. 1(b) "노이즈가 있는" 2D 나선형

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\] Eqn. 1(a) \[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] Eqn. 1(b)

분류 를 한다는 것은 무슨뜻일까? 로지스틱 회귀 의 경우를 살펴보자. 만일 분류를 위한 로지스틱 회귀를 이 데이터에 적용한다면, 이는 선형 평면 (결정 경계) 의 집합을 만들어서 데이터를 각각의 클래스에 맞게 분류해 내려고 할 것이다. 하지만 이 해결법의 문제점은 각 지역에 대해, 여러 클래스에 동시에 속하는 점들이 존재한다는 것이다. 나선형의 가지는 결정 경계인 선형 평면을 가로지른다. 이는 훌륭한 해결책이 아니다 !

이 문제를 어떻게 해결해야 할까? 우리는 데이터가 선형으로 분류될 수 있도록 입력 값들을 변환한다. 이를 위한 신경망을 훈련시키는 동안, 이 신경망이 학습하는 결정 경계는 학습 데이터의 분포에 따라 조정될 것이다.

주의할 점: 신경망은 항상 아래 에서 부터 표현된다. 첫번째 층^layer은 맨 아래에, 그리고 마지막 층은 최 상단에 존재한다. 왜냐하면, 개념적으로 입력 데이터는 신경망이 달성하고자 하는 목표 작업에 대해 낮은 수준의 특징값으로 간주되기 때문이다. 데이터가 신경망을 통해 위 로 통과 해 나갈 때, 각 후속 층에서는 더 높은 수준의 데이터 특징을 추출한다.

학습 데이터

지난주, 우리는 새로이 초기화된 신경망이 입력 데이터를 임의의 방식으로 변환하는 것을 확인했다. 그러나, 이 변환은 당면한 작업을 수행하는데 있어 (초기에) 유용한 것은 아니다. 우리는 데이터를 이용해서 어떻게 이 변환이 현재의 작업과 관련해 의미가 있도록 할 수 있는지 살펴본다. 다음은 신경망의 학습에 이용되는 입력 데이터이다.

• $\vect{X}$ 는 입력 데이터로써, $m$ (학습할 데이터 포인트의 갯수) x $n$ (각 입력 포인트의 차원) 차원의 행렬이다. 그림 1(a) 과 1(b) 에 보여지는 데이터의 경우 $n = 2$ 이다.

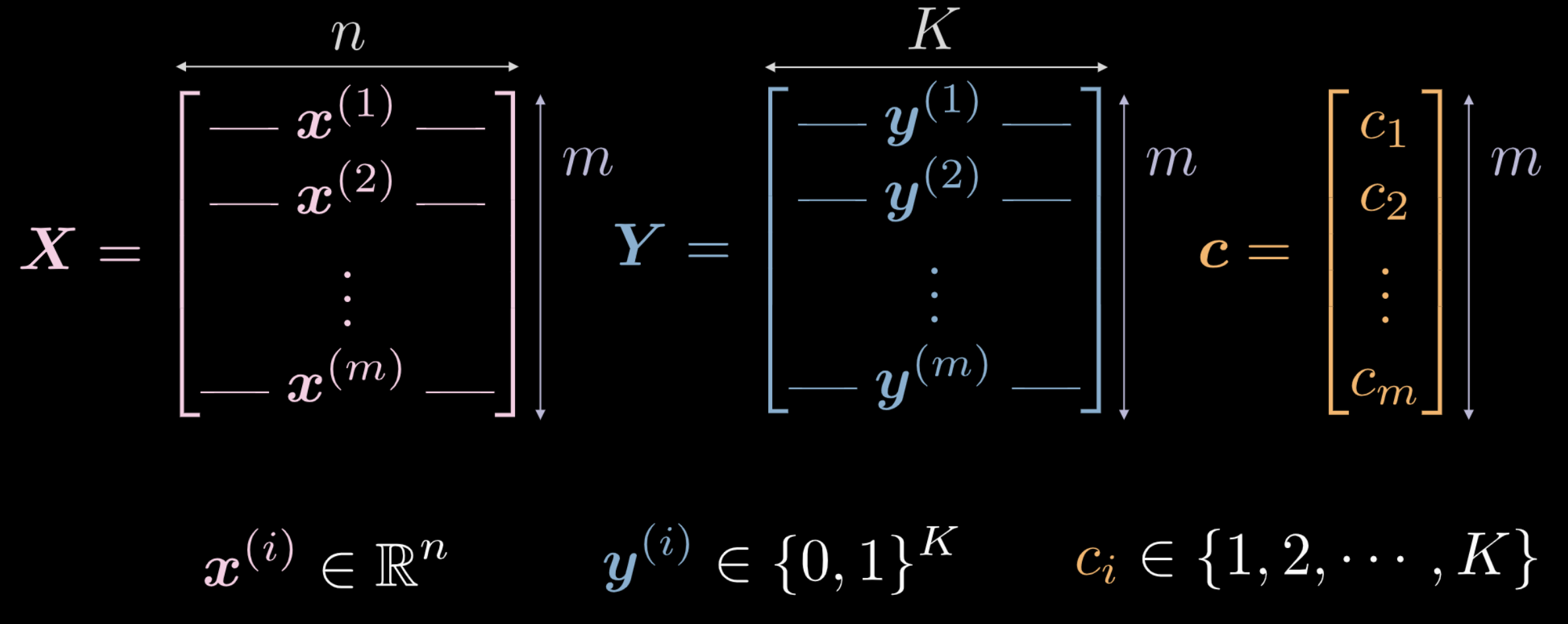
Fig. 2 학습 데이터

• 벡터 $\vect{c}$ 와 행렬 $\boldsymbol{Y}$ 은 모두 각 $m$ 개의 데이터 포인트에 대한 클래스 레이블을 나타낸다. 위의 예시에는 $3$ 개의 고유한 클래스가 있다.

  • $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, and $\vect{c} \in \R^m$. 그러나, 우리는 $\vect{c}$ 을 학습 데이터로 활용하지는 않을 것이다. 만일 우리가 고유한 클래스 레이블 $c_i \in \lbrace 1, 2, \cdots, K \rbrace$ 을 그대로 사용한다면, 신경망은 데이터 분포와는 연관이 없는 개별 클래스 사이의 순서를 유추해낸다.
  • 이러한 문제점에 대응하기 위해, 우리는 원-핫 인코딩 을 사용한다. 각각의 클래스 레이블 $c_i$ 에 대하여, $c_i$ 번 째 원소가 $1$ 인 $K$ 차원의 영백터^{zero vector} $\vect{y}^{(i)}$ 가 만들어진다 ( 아래의 Fig. 3 에서 확인할 수 있다).

Fig. 3 원-핫 인코딩

• 따라서, $\boldsymbol Y \in \R^{m \times K}$ 와 같다. 또한 이 행렬은 $K$ 지점 중 하나에 집중된 확률적 질량^{probabilistic mass}을 가진 것으로도 여겨질 수 있다.

완전 연결^{Fully Connected, FC} 계층^layers

이제 우리는 완결 연결 네트워크^{fully connected (FC) network} 가 무엇이고, 이것이 어떻게 작동하는지 살펴본다.

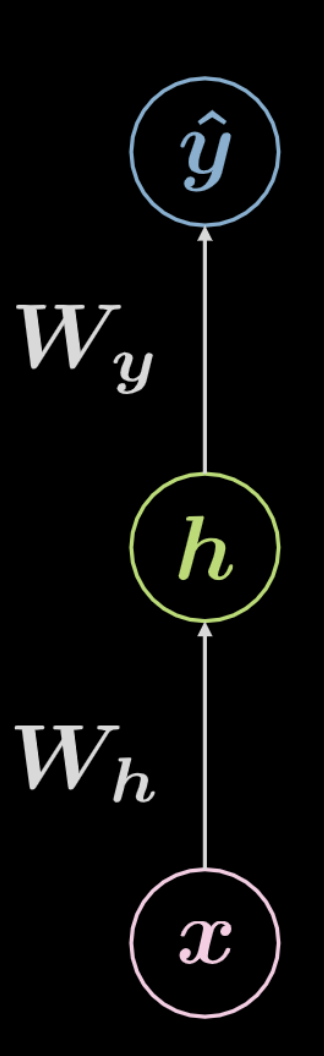
Fig. 4 완전 연결 신경망

위의 Fig. 4 의 신경망을 살펴보자. 입력 데이터, $\boldsymbol x$, 는 $ \boldsymbol W_h$ 로 정의된 아핀 변환에 이어 비선형 변환이 적용되게 된다. 이 비선형 변환의 결과는 $\boldsymbol h$ 로 표현되고, 이는 은닉^hidden 출력값을 나타내는데, 즉 신경망의 외부에서는 보이지 않는다. 뒤이어 또다른 아핀 변환 ($\boldsymbol W_y$) 과 또다른 비선형 변환이 이어진다. 이는 최종 출력인 $\boldsymbol{\hat{y}} $ 을 만든다. 이 신경망은 아래의 수식 Eqn. 2 을 통해서도 표현될 수 있다. \(f\) 와 \(g\) 는 모두 비선형이다.

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] Eqn. 2 완전 연결 신경망의 바탕이 되는 수학

. 위에서 보여진 것과 같은 기본 신경망은 단지 아핀 변환과 그 뒤에 이어지는 비선형 연산(스쿼싱^squashing)으로 짝을 이룬 연속적인 쌍의 의 모임에 불과하다. 빈번하게 사용되는 비선형 함수에는 ReLU, 시그모이드^sigmoid, 쌍곡 탄젠트^{hyperbolic tangent}, 그리고 소프트맥스^softmax 등이 있다.

상단에 보여진 것은 3층 신경망이다:

1. 입력 뉴런^neuron
2. 은닉 뉴런
3. 출력 뉴런

따라서, $3$-층 신경망은 $2$ 개의 아핀 변환을 가진다. 이러한 내용은 $n$-층 신경망으로 확장될 수 있다.

그럼 이제, 조금 더 복잡한 사례로 넘어가보자.

3개의 은닉층이 서로 완전히 연결된 경우를 살펴보자. 이에 대한 그림은 Fig. 5 에서 확인할 수 있다.

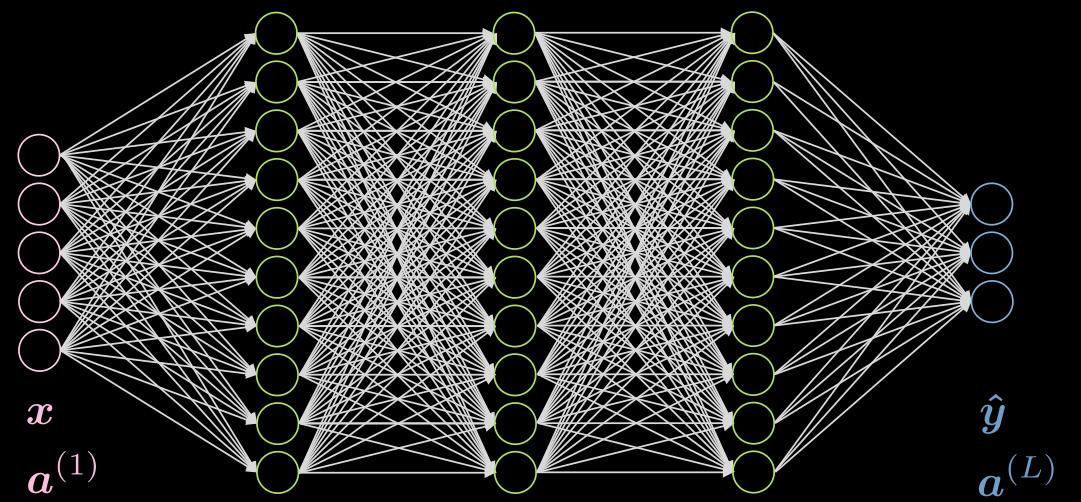
Fig. 5 3개의 은닉층으로 구성된 신경망

두 번째 층의 $j$ 번 째 뉴런을 살펴보자. 이것의 활성화는 다음과 같다.:

\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]

여기에서 $\vect{w}^{(j)}$ 은 $\vect{W}^{(1)}$ 의 $j$-번 째 행이다.

여기서 입력층의 활성화는 단지 항등^identity임을 알 수 있다. 은닉층은 ReLU, 쌍곡탄젠트, 시그모이드, 소프트맥스^{soft (arg)max} 등을 활성화로 가질 수 있다.

일반적으로 마지막 층의 활성화는 여기의 Piazza 글에서 확인할 수 있듯 구체적인 상황 및 목적에 따라 달라진다.

신경망 (추론)

3층(입력, 은닉, 출력) 신경망에 대해 다시 한 번 생각해보자. 이는 Fig. 6 에서 확인할 수 있다.

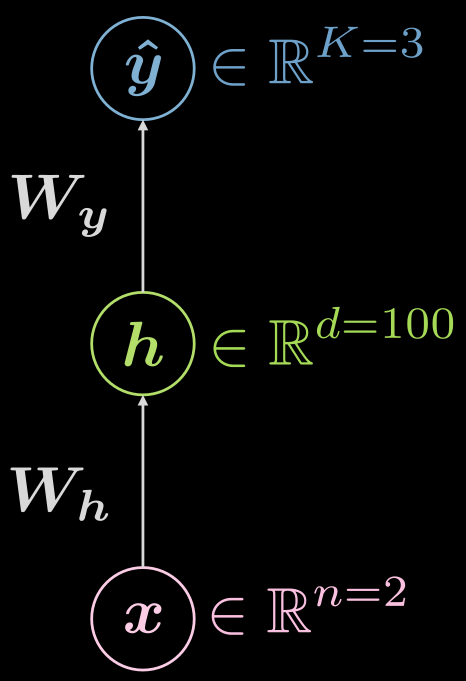
Fig. 6 3층 신경망

지금 우리가 보고 있는 이 함수들은 어떤 기능을 할까?

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

그러나, 은닉층이 있다는 사실을 보여주는 것은 도움이 되며, 이 매핑^mapping은 다음과 같이 전개된다.:

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

위의 사례와 같은 구성 예시는 어떤 것이 있을까? 이 경우, 2차원($n=2$)의 입력을 가지고, 단일한 은닉층은 1000 ($d = 1000$) 개의 차원을 가지며, 3개의 클래스 ($C=3$) 를 가진다. 그런데 하나의 은닉층이 지나치게 많은 뉴런을 가져서는 안되는 실질적인 이유가 있기 때문에, 단일 은닉층을 10개의 뉴런을 가진 3개의 층으로 나누는 것이 좋다 ($1000 \rightarrow 10 \times 10 \times 10$).

신경망 (학습 I)

그렇다면, 일반적인 훈련은 어떤 모습일까? 이를 손실에 대한 표준적인 용어로 공식화 하는 것은 도움이 된다.

먼저, 소프트맥스^{soft (arg)max}을 다시 소개하고, 다중 클래스^multi-class 예측 상황에서 로그 우도^{log-likelihood} 손실을 사용할 때 이것이 마지막 출력층에서 가장 널리 쓰이는 활성화임을 명확하게 밝히자. 이에 대한 이유는 지난 강의에서 르쿤^LeCun 교수가 말했듯, 이 활성화가 시그모이드^sigmoid와 제곱 손실^{square loss}을 사용할 때 보다 더 유용한 경사^gradients 값을 제공하기 때문이다. 뿐만 아니라, 여기에서 마지막 출력층은 명시적 정규화 (놈^norm 으로 나누는 것) 보다 경사 하강법에 더 좋은 방식으로 이미 정규화가 되어 출력된다 (마지막 층의 모든 뉴런의 합계는 1이 됨).

소프트맥스는 다음과 같이 마지막 층에서 로짓^logit 값을 제공한다.:

\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]

여기에서 지수 함수가 엄격한 양수의 특성^{strictly positive nature}을 지니기 때문에 이 집합이 닫히지 않은 것을 알아둘 필요가 있다.

$\matr{\hat{Y}}$ 의 예측 집합이 주어졌을 때, 손실은 다음과 같다.:

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]

여기에서 c 는 원-핫 인코딩 표현이 아니라, 정수 레이블^label을 나타낸다.

한 예시는 잘 분류가 됐으나, 나머지 하나는 그렇지 않은 두 개의 예시를 살펴보자.

만일 다음과 같다면,

\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]

각 인스턴스^instance의 손실은 어떻게 될까?

거의 완벽한 예측 예시 ($\sim$ 는 거의^circa 를 의미한다):

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]

거의 절대적으로 옳지 않은 예시:

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]

위의 예시에서, $\sim 0 \rightarrow 0^{+}$ 이고, $\sim 1 \rightarrow 1^{-}$ 이다. 왜 그럴까? 잠시 시간을 갖고 생각해 보기 바란다.

주의할 점: 만일 크로스엔트로피 손실<sup>CrossEntropyLoss</sup>을 사용하면, 로그소프트맥스<sup>LogSoftMax</sup> 와 음의 로그 우도^{negative loglikelihood} NLLLoss 가 함께 도출된다는 점을 알아둘 필요가 있다. 그러니 두 번 하지 마라!

신경망 (학습 II)

학습을 시키기 위해 우리는 학습이 가능한 모든 매개 변수 – 가중치 행렬과 오차 – 를 다음과 같은 집합 $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$ 에 집계한다. 이를 바탕으로 목적 함수 또는 손실을 다음과 같이 작성할 수 있다.:

\[J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]

이는 신경망의 출력 $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$ 에 손실이 의존하도록 하고, 따라서 이를 최적화 문제로 바꿀 수 있다.

이것이 어떻게 작동하는지에 대한 간단한 설명은 최소화해야 하는 함수 $J(\vartheta)$ 가 오직 하나의 스칼라 매개변수 $\vartheta$ 만을 가지는 Fig. 7 에서 확인할 수 있다.

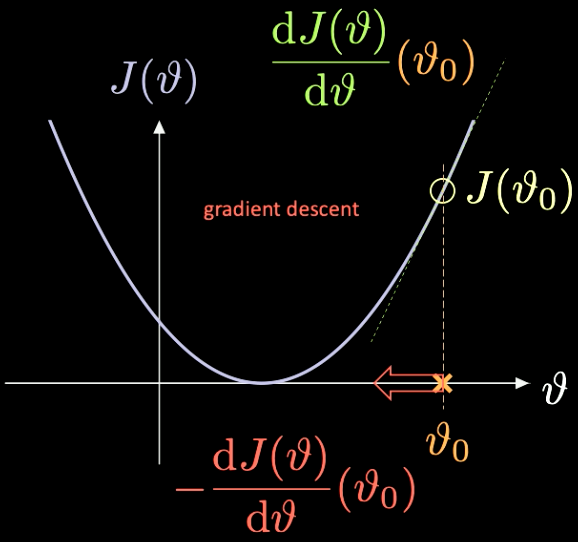
Fig. 7 경사하강법을 통한 손실 함수 최적화.

우리는 임의의 초기화 점 $\vartheta_0$ 을 선택한다 – 여기서의 손실은 $J(\vartheta_0)$ 이다. 이 점에서 계산되는 미분값은 $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$ 과 같다. 이 경우, 계산된 미분값의 기울기는 양수이다. 따라서 우리는 가장 가파른 방향으로 나아가야 하고, 이는 $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$ 과 같다.

이를 반복하는 과정을 경사 하강법 ^{gradient descent} 이라고 한다. 경사 하강법은 신경망을 학습시키는 가장 기본적인 도구이다.

필요한 경사를 계산해 내기 위해 우리는 역전파^{back-propagation}를 사용한다.

\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]

나선형 분류 - 주피터 노트북

이 실습과 관련된 주피터 노트북은 여기에서 확인할 수 있다. 이 주피터 노트북을 실행하기 위해서, README.md 에서 설명된 것과 같이 the dl-minicourse 이 작업 환경에 설치가 됐는지 확인해야 한다.

torch.device() 의 사용 방법에 대한 설명은 지난 주 강의 노트 에서 확인할 수 있다.

이전과 동일하게, 우리는 세 가지 범주형^categorical 레이블 - 빨강, 노랑, 파랑 - 을 가지는 $\mathbb{R}^2$ 위의 점들을 다룬다. 이는 Fig. 8 에서 확인할 수 있다.

Fig. 8 나선형 분류 데이터.

nn.Sequential() 은 컨테이너^container로써, 컨테이너에 모듈이 추가된 순서로 생성자에게 모듈을 전달한다; nn.linear() 는 사실 이름이 잘못 지어졌는데, 이 함수는 입력된 데이터에 대해 affine 변환을 수행한다 : $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$. 자세한 내용은 파이토치 문서 를 참조하기 바란다.

아핀 변환은 회전^{rotation, 반사reflection, 변환translation, 스케일링scaling, 절단shearing의 다섯 가지임을 기억하자.}

그림 Fig. 9 에서 볼 수 있듯, 나선 데이터를 선형 결정 경계 - 비선형성 없이 오직 nn.linear() 모듈만을 사용 - 로 분류해 내고자 하면, 우리가 이룰 수 있는 가장 높은 정확도는 50% 이다.

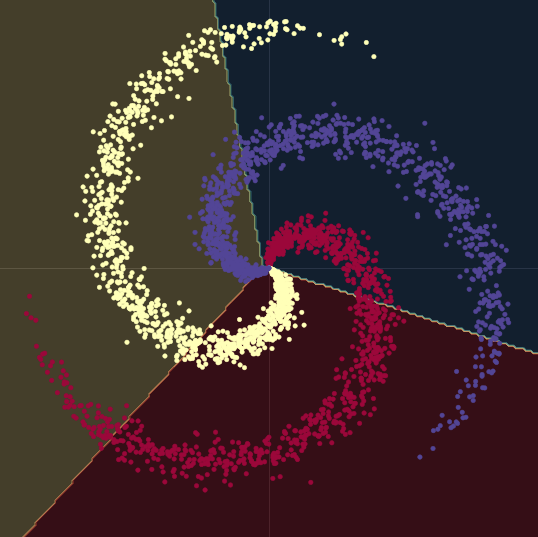
Fig. 9 선형 결정 경계.

이 선형 모델을, 두 개의 nn.linear() 모듈 사이에 nn.ReLU() 을 끼운 모델로 바꾸면, 모델의 정확도는 95%로 상승한다. 그림 Fig. 10 에서 볼 수 있듯, 결정 경계가 비선형으로 바뀌어 나선형 데이터 형식에 더 적합해지기 때문이다.

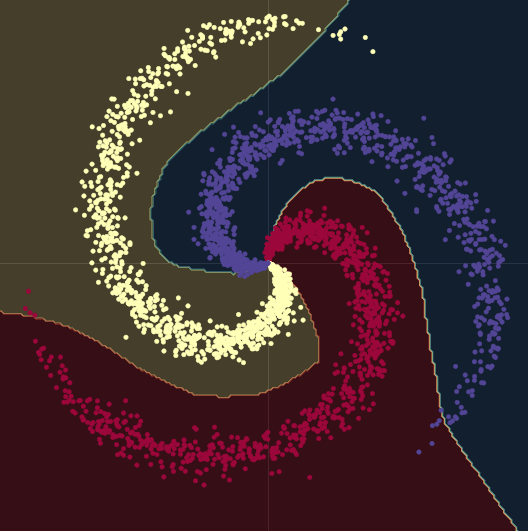
Fig. 10 비선형 결정 경계.

선형 회귀로는 올바르게 해결할 수 없지만, 동일한 신경망 구조로 쉽게 해결되는 회귀 문제의 예는 이 노트북에서 확인할 수 있고, 그림 Fig. 11 을 통해 절반은 nn.ReLU()을 연결 함수로, 그리고 나머지 절반은 nn.Tanh() 을 이용한 10개의 신경망을 확인할 수 있다. 전자^nn.ReLU()는 부분 선형 함수인 반면, 후자^nn.Tanh()는 연속적이고 부드러운 회귀이다.

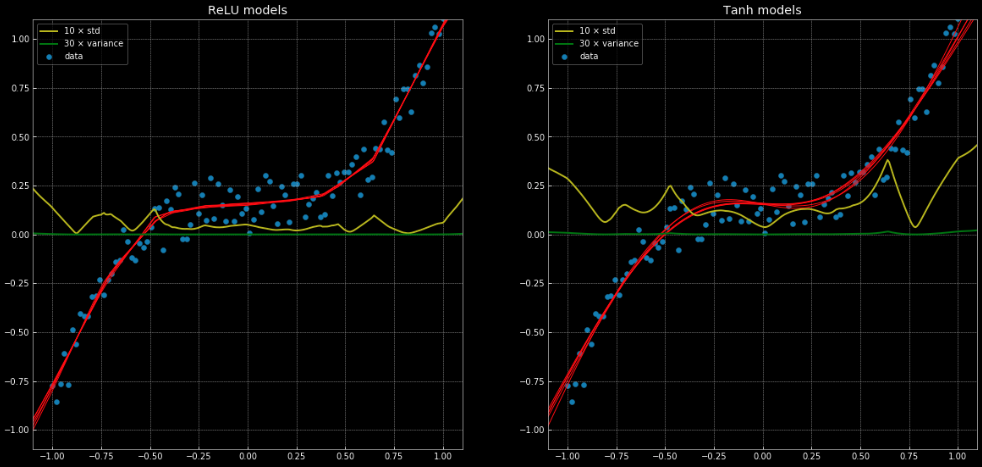
Fig. 11: 분산 및 표준편차와 함께 제시된 10개의 신경망.
왼쪽: 다섯개 ReLU 구조^network. 오른쪽: 다섯개 tanh 구조.

노란색과 초록색 선은 신경망의 표준 편차와 분산을 나타낸다. 이것들을 사용하는 것은 “신뢰 구간” 과 비슷하게 유용한데, 함수들이 각 출력 당 하나의 예측을 내놓기 때문이다. 앙상블^ensemble 분산 예측을 사용하면 결과로 나온 예측과 관련된 불확실성을 추정할 수 있다. 이것의 중요성은 Fig. 12 을 통해 확인할 수 있는데, 여기서 우리는 결정 경계를 데이터 범위 바깥으로 확장시키고, 이 경계들은 $+\infty, -\infty$ 로 향하는 경향이 있다.

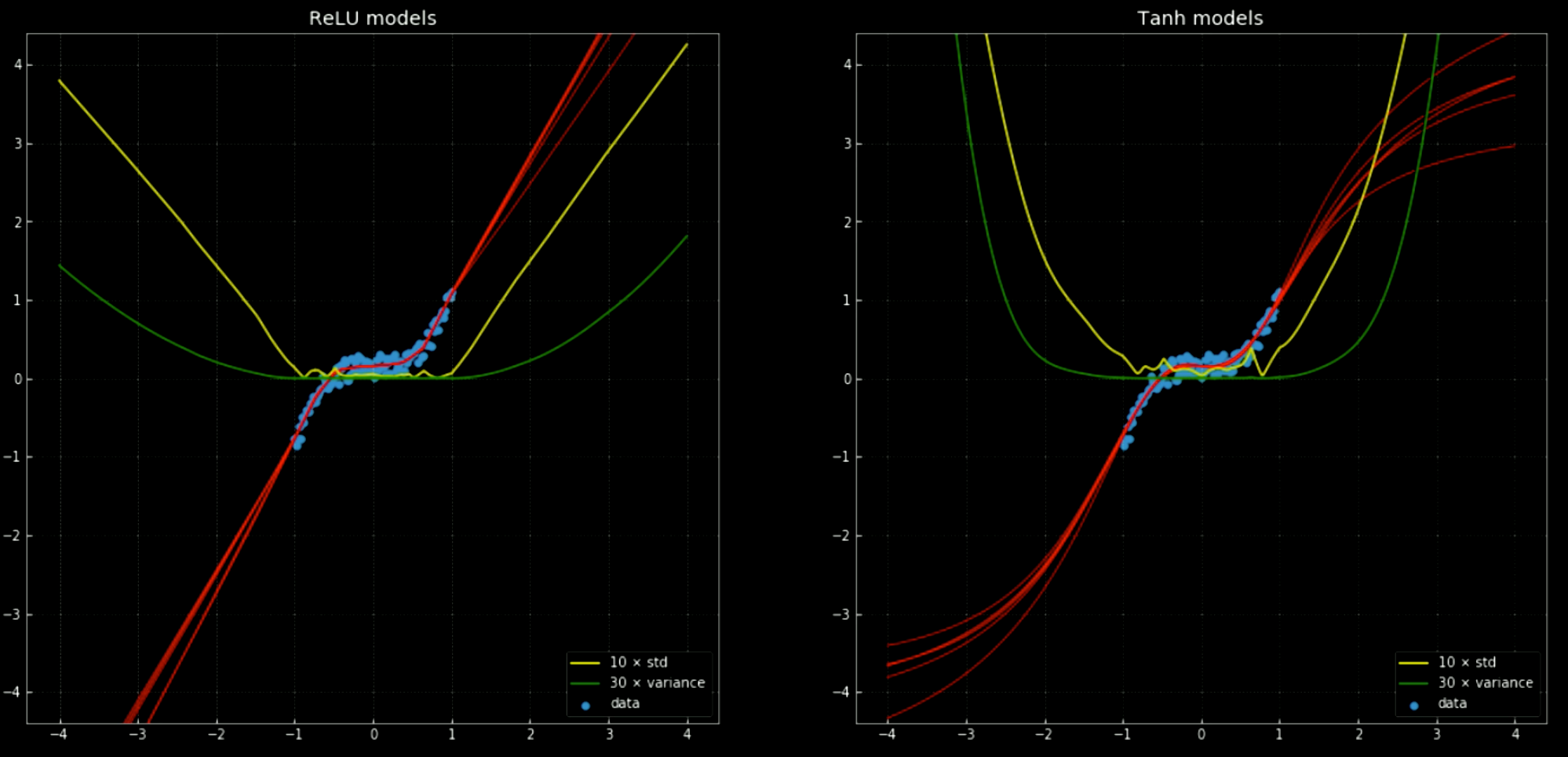
Fig. 12 훈련 범위를 바깥의 분산 및 표준편차가 있는 신경망.
왼쪽: 다섯개 ReLU 구조. 오른쪽: 다섯개 tanh 구조.

파이토치를 이용해 신경망을 학습시키기 위해서, 학습 루프^loop 안에서 5개의 기본 단계를 거쳐야 한다:

1. output = model(input) 은 모델의 전달 경로로써, 입력을 받아 출력을 생성한다.
2. J = loss(output, target <or> label) 는 모델의 출력이 실제 목표 또는 레이블에 대해 얼만큼의 훈련 손실을 보이는지 계산한다.
3. model.zero_grad() 는 이전에 계산된 경사값들을 0으로 정리해서 다음 전달 경로에 과거의 계산값들이 축적되지 않도록 한다.
4. J.backward() 는 역전파 및 축적을 수행한다: 우리가 requires_grad=True 로 지정한 모든 변수 $\texttt{x}$에 대해서 $\nabla_\texttt{x} J$ 을 계산한다. 이 계산 값들은 각 변수의 경사값에 누적된다: $\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$.
5. optimiser.step() 는 경사 하강법을 한 단계 수행한다: $\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$.

신경망을 학습시킬 때에는, 위에서 5개 단계가 제시된 순서에 따라 학습을 진행하는 것이 권장된다.

---

Yujin
4 Feb 2020