NN 모듈의 경사 연산과 역전파를 위한 실용적인 학습 기법

역전파와 기본적인 인공신경망 모듈에 대한 구체적인 예시

예시

우리는 역전파에 대한 구체적인 예시를 그래프 시각자료를 통하여 살펴본다. 임의의 함수 $G(w)$는 손실 함수 $S$의 입력으로 사용된다. 이때 손실함수 역시 그래프로 표현 가능하다. 야코비안 행렬^{Jacobian matrics}의 행렬 곱 연산을 통하여, 그래프로 표현된 손실함수는 그 기울기를 역전시킬수 있는 그래프로 변환할 수 있다. (Pytorch와 TensorFlow는 위 파이썬 라이브러리 사용자들을 위해서 위 작업들의 자동화를 지원한다. 예를 들어서 기울기를 역전파하는 미분 그래프를 생성하기 위해서 순전파 그래프는 자동으로 역전된다.)

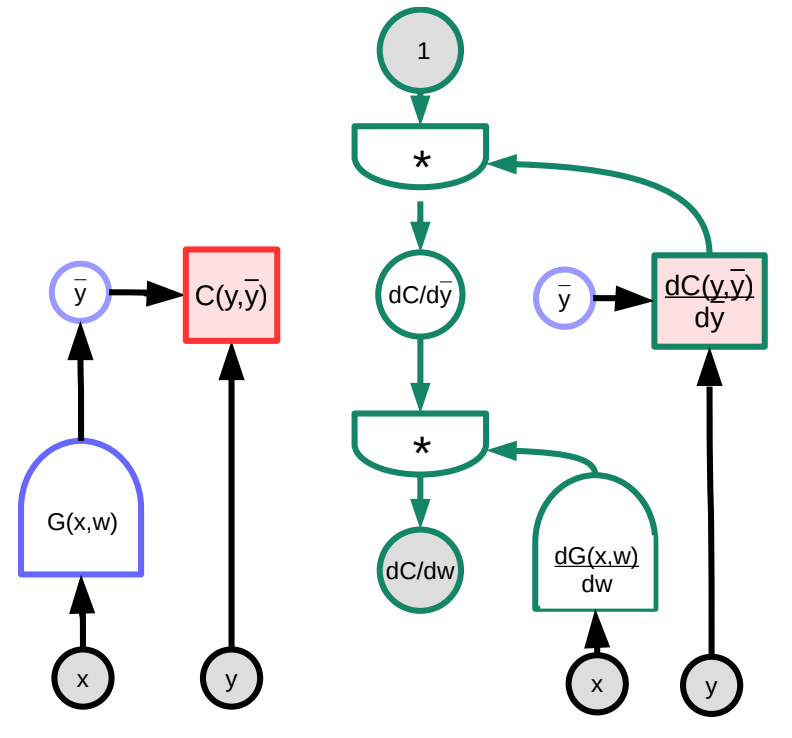
위 예시에 있어서, 오른쪽에 있는 초록색 그래프는 기울기를 역전시키는 그래프이다. 최상위 노드의 그래프는 다음과 같이 표현이 가능하다.

차원의 관점에서, $\frac{\partial C(y,\bar{y})}{\partial w}$는 $1\times N$ 크기의 행 벡터이다. 여기서 $N$는 $w$의 구성 요소 수이다.$\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ 은 $1\times M$ 크기의 행 벡터이다. 여기서 $M$은 출력의 차원이다. $\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ 은 $M\times N$ 행렬 크기를 가지게 된다. 여기서 $M$는 $G$의 출력 수이고 $N$는 $w$의 차원이다.

그래프의 구조가 고정되어있지 않더라도, 데이터에 따라서 복잡성이 발생할 수 있다. 예를 들어 입력 벡터의 길이에 따라서 우리는 신경망 모듈을 선택할 수 있다. 루프의 수가 연산 가능한 양을 초과하게 된다면, 변화에 대한 관리가 점점 더 어려워지는 문제가 발생할 수 있다.

간단한 신경망 모듈

익숙한 선형 모듈과 ReLU 모듈 이외에도 다양한 유형의 미리 만들어 놓은 모듈이 있다. 이들은 각각의 기능을 수행하기 위해 고유하게 최적화되어 있기 때문에 편리하다. (다른 기본 모듈의 조합에 의해 구축되는 것이 아니다)

• Linear: $Y=W\cdot X$

• ReLU: $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{otherwise} \end{cases}\]

• Duplicate: $Y_1=X$, $Y_2=X$

  • 두 출력이 입력과 동일한 ‘Y- 스플리터’과 비슷하다.
  • 역전파가 진행되면서, 기울기가 모두 더해진다.

  • N개의 지점으로 나눌 수 있다.

    \[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]

• Add: $Y=X_1+X_2$

  • 두 변수가 합산됨에 따라서, 하나의 변수가 변동함에 따라서, 다른 변수도 동일한 양으로 변동하게 될 것이다. 아래의 수식을 통해 예시를 확인할 수 있다.

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{and}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• Max: $Y=\max(X_1,X_2)$

  • 위 함수는 아래와 같이 표현할 수 있다.

• • 연쇄 법칙에 따르면 다음과 같이 정리할 수 있다.

LogSoftMax vs SoftMax

Pytorch 모듈이기도 한 SoftMax는 일정한 시퀀스의 숫자들을 $0$과 $1$ 사이의 양의 수로 변환하는 방법을 뜻한다. 이러한 숫자는 확률 분포로 해석될 수 있다. 이러한 성질로 인하여, 일반적으로는 분류 문제에서 사용된다. 아래 방정식에서 $ y_i $는 모든 카테고리에 대한 확률의 벡터를 말한다.

그러나 softmax를 사용하면 신경망은 기울기 손실^{vanishing gradients}에 취약해진다. 기울기 손실 문제는 학습이 진행됨에 따라서, 손실 함수의 기울기가 인공 신경망의 각 계층에 전달되면서 신경망의 가중치가 학습되는 것을 막는다. 예를 들어, 단일 값에 대한 softmax 함수인 logistic sigmoid 함수는 $s$가 크면 $h(s)$가 $1$이고 $s$가 작을 때 $h(s)$가 $0$임을 나타낸다. $h(s)=0$ 및 $h(s)=1$에서 평평한 경우, 기울기는 $0$이므로 기울기 손실이 발생하게 된다.

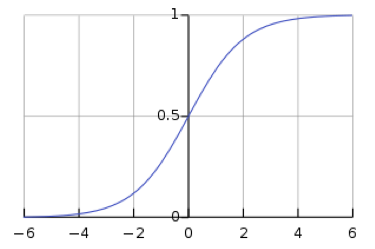
\(h(s) = \frac{1}{1 + \exp(-s)}\)

수학자들은 Softmax의 기울기 손실 문제를 해결하기 위해서 logsoftmax라는 아이디어를 가지고 나오게 된다. LogSoftMax는 또한 Pytorch의 기본 모듈이다. 아래 수식처럼, LogSoftMax는 softmax와 log함수의 결합이다.

\(\log(y_i )= \log\left(\frac{\exp(x_i)}{\Sigma_j \exp(x_j)}\right) = x_i - \log(\Sigma_j \exp(x_j)\) 아래 방정식은 동일한 방정식을 보는 다른 방법을 보여준다. 아래 그림은 함수의 $\log(1 + \exp(s))$ 부분이다. $s$가 매우 작은 경우 값은 $0$이고 $s$가 매우 큰 경우 값은 $s$이다. 결과적으로 결과값이 포화되지 않고, 기울기 손실 문제를 피할 수 있다.

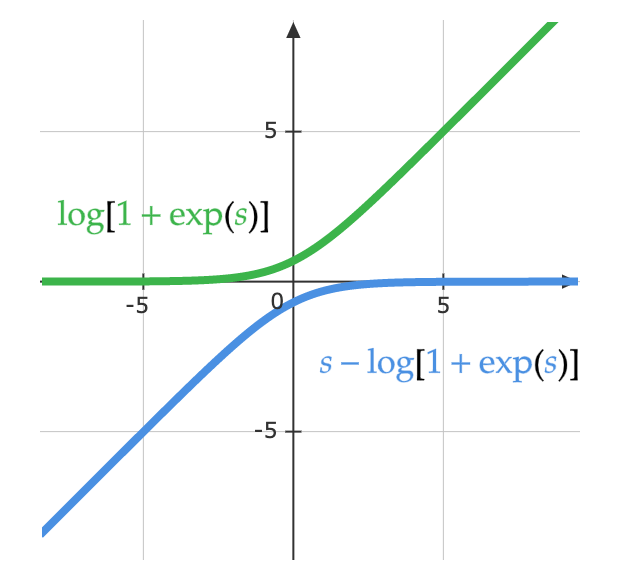
역전파 학습을 위한 실용적인 학습 기법

ReLU를 비선형 활성화 함수로 사용한다.

ReLU는 여러 계층의 네트워크에서 가장 잘 작동하는 비선형 함수이다. ReLU의 대안으로 사용되는 sigmoid 함수 및 $\tanh(\cdot) $ 함수와 같은 비선형 함수보다 선호된다. ReLU가 가장 잘 작동하는 이유는 하나의 꺽인점_kink만 사용해서 등가 스케일링이 가능하기 때문이다. <!–

Use cross-entropy loss as the objective function for classification problems –>

분류 문제를 다룰 때 cross-entropy loss를 목적 함수로 사용하기

Log softmax, which we discussed earlier in the lecture, is a special case of cross-entropy loss. In PyTorch, be sure to provide the cross-entropy loss function with log softmax as input (as opposed to normal softmax).

앞서서 논의한 Log softmax는 cross-entropy loss의 특별한 경우이다. Pytorch는 입력으로 log softmax를 사용하여 cross-entropy loss를 제공한다 (일반 softmax와 반대).

학습시 미니 배치상에서의 확률적 경사 하강 사용

앞에서 설명한 것처럼, 데이터내에 중복성이 존재하기 때문에 미니 배치를 통해서 효율적으로 학습시킬 수 있다. 기울기를 연산하기 위해, 모든 단계에서 모든 관측치에서 예측하고, 손실을 계산할 필요는 없다.

확률적 경사 하강을 사용할 때 훈련 데이터의 Shuffle

학습에서 순서는 중요하다. 만약 모델이 각 학습 단계에서 단일 클래스의 예제만 보는 경우 해당 클래스를 예측해야하는 이유를 배우지 않고 해당 클래스를 예측하는 방법을 학습한다. 예를 들어 섞이지 않은 MNIST dataset의 digits을 학습하는 경우에 있어서, 마지막 레이어의 Bias 파라미터는 항상 0으로 예측된다. 이러한 경우, 항상 1이나 2가 되도록 분류기는 적응한다. 이상적으로는 모든 미니 배치마다 훈련 데이터를 섞는 것이 중요하다.

그러나 모든 Epoch 에서 훈련데이터의 순서를 변경해야 하는지에 대한 논의는 진행중이다.

평균이 0이고 분산이 1이 되도록 입력을 일반화하기

학습하기 전에, 각 입력 기능을 일반화하여 평균이 0이고 표준 편차가 1이 되도록 하는 것이 유용하다. RGB 이미지 데이터를 사용하는 경우에는 각 채널의 평균 및 표준 편차를 개별적으로 취하여 이미지를 채널 단위로 일반화하는 것이 일반적이다. 예를 들어 데이터 세트에 있는 모든 파란색 값의 평균 $m_b$ 및 표준 편차 $\sigma_b$를 취한 다음, 각 이미지의 파란색 값을 일반화한다

여기서 $\epsilon$은 0으로 나누는 경우를 피하기 위해 임의로 사용하는 작은 숫자이다. 초록색 및 빨간색 채널에 대해서도 동일한 과정을 수행한다. 이 과정은 다른 광량에서 촬영한 이미지내에서 의미있는 신호를 얻는데 필요하다. 예를 들어, 자연광 사진에는 빨간색이 많고, 수중에서 촬영한 사진에는 빨간색이 거의 없다.

학습 속도를 줄이는 Schedule 사용

훈련이 진행됨에 따라 학습률^{learning rate}를 감소시켜야한다. 실제 학습에 있어서, 대부분의 Advanced Model은 Adam과 같은 알고리즘을 사용하게 되는데, 이것은 고정된 학습률을 쓰는 간단한 SGD가 아니라 적응형 학습률을 사용한다.

Weight Decay를 위한 L1, L2 정규화 사용

Cost Function에 있어서 큰 가중치에 대해서 우리는 추가적인 Cost를 추가할 수 있다. 예를 들어서 L2정규화를 사용한다면, 우리는 손실 $L$을 다음과 같이 정의하고, 가중치 $w$를 다음과 같이 업데이트 할 수 있다.

\(L(S, w) = C(S, w) + \alpha \Vert w \Vert^2\\ \frac{\partial R}{\partial w_i} = 2w_i\\ w_i = w_i - \eta\frac{\partial L}{\partial w_i} = w_i - \eta \left( \frac{\partial C}{\partial w_i} + 2 \alpha w_i \right)\) 우리가 이것을 왜 weight decay라고 부르는지 이해하기 위해서는, 업데이트 중에 $w_i$에 1보다 작은 상수를 곱한 것을 확인할 수 있게끔, 위 식을 아래와 같이 다시 적어보면 알 수 있다.

\(w_i = (1 - 2 \eta \alpha) w_i - \eta\frac{\partial C}{\partial w_i}\)

L1 정규화 (Lasso) 역시 유사하다. $\Vert w \Vert^2$ 대신에 $\sum_i \vert w_i\vert$ 을 사용하는 부분에서 차이가 있다.

기본적으로, 정규화는 가능한 가장 짧은 가중치 벡터를 가지고 비용 함수를 최소화하도록 시도한다. L1 정규화를 사용하면, 유용하지 않은 가중치는 $0$으로 줄어줄게 된다.

가중치 초기화

가중치는 무작위로 초기화해야하지만, 출력이 입력과 거의 동일한 분산을 갖도록 너무 크거나 작지 않아야 한다. PyTorch에는 다양한 가중치 초기화 트릭이 내장되어 있다. 심청적인 모델에 효과적인 트릭 중 하나는 가중치의 분산이 입력 수의 제곱근에 반비례하는 Kaiming 초기화 함수를 사용하는 것이다.

드롭아웃 사용

드롭아웃은 또 다른 형태의 정규화 방법이다. 어떻게 보면, 신경망의 또 다른 계층으로 생각할 수도 있다. 입력 노드를 받아서 입력노드의 $n/2$ 를 임의로 0으로 설정하고 결과로 줄어든 출력 노드로 반환한다. 이로 인해 시스템은 적은 수의 입력 노드에 지나치게 의존하지 않고 모든 입력 노드로부터 정보를 가져와서 레이어의 모든 노드에 정보를 분배하게 된다. 이 방법은 처음에 Hinton et al (2012) 에서 제안되었다.

더 많은 학습 트릭을 확인하고 싶으면, 다음의 문서를 참고하길 바란다. LeCun et al 1998.

마지막으로 역전파는 계층들이 쌓여 있는 Stacked 모델에 대해서만 작동하는 것은 아니다. 모듈간에 부분적으로 순서가 있는 DAG (directed acyclic graph)에 대해서도 동작할 수 있다.