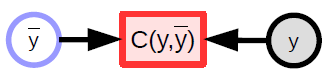경사하강법과 역전파 알고리즘

경사 하강 최적화 알고리즘

매개변수화된 모델

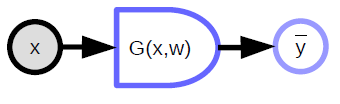
매개변수화된 모델은 입력과 학습가능한 매개변수에 의해서 결정되는 간단한 함수를 말한다. 이 두 개의 변수간에 원론적인 차이점은 없지만, 한가지 다른 부분은 학습가능한 매개변수는 샘플들이 학습되는 동안에 서로간에 공유가 되지만, 입력은 샘플과 샘플마다 다르다는 것이다. 최근에 출시된 딥러닝 프레임워크에서는 매개변수들이 함축적으로 정의되어 있는데, 이 말은, 함수가 호출될 때 포함되어 있지 않다는 것을 의미한다. 적어도 객체-기반으로 구현된 모델을 바탕으로 굳이 말하자면, 이 변수들은 ‘함수 내부에 저장되어’ 있는 것이다.

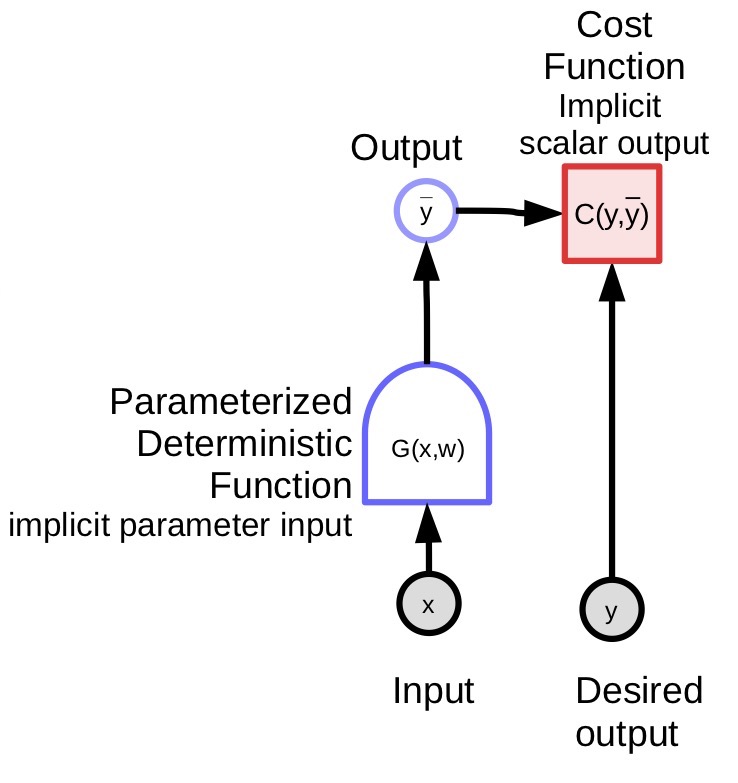
매개변수화된 모델 (함수)는 입력을 받고, 매개변수 벡터를 가지고 있으며, 이를 이용해서 출력을 만들어낸다. 지도 학습에서는 이 출력값이 비용 함수 ($C(y,\bar{y}$)) 로 들어가는데, 이 함수는 실제의 출력값 (${y}$) 과 모델에서 생성된 출력값 ($\bar{y}$)을 비교해주는 역할을 한다. 이 모델에 대한 연산 그래프는 그림 1에서 보여주고 있다.

그림 1: 매개변수화된 모델에 대한 연산 그래프

매개변수화된 함수의 예시

• 선형 모델 - 입력 벡터의 각 요소들에 대한 가중합:

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• 최근접 이웃 - 입력 x와 k로 인덱싱할 수 있는 행을 가진 가중치 행렬 W가 있다. 이때의 출력은 k의 값 자체가 될텐데, 이 값은 x와 가장 가까운 W의 행을 나타낸다.:

  \[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

  매개변수화된 모델은 복잡한 함수와도 관련있을 수 있다.

연산 그래프에 대한 각 요소에 대한 표현

• 변수 (텐서, 스칼라, 연속적인 값, 비연속적인 값)
  • 는 시스템상에서 관찰된 입력값이다.
  • 는 결정적 함수에 의해서 생성된 계산된 값이다.

• 결정적 함수

  

  • 여러 개의 입력을 받고 여러 개의 출력을 생성한다.
  • 내부적으로 함축된 매개변수 (${w}$) 를 가지고 있다.
  • 곡선으로 나타난 부분은 어느 쪽이 계산하기 쉬운지를 방향으로 표현한 것이다. 위의 다이어그램에서는 ${x}$ 으로부터 ${\bar{y}}$ 를 계산하는 것이 다른 방법보다 쉽다.

• 스칼라 값을 가지는 함수

  

  • 비용 함수를 나타낼 때 사용한다.
  • 내부적으로 함축된 출력을 가지고 있다.
  • 다수의 입력을 가지고, 하나의 값을 출력으로 내보낸다. (보통 입력들간의 거리를 표현한다.)

손실 함수

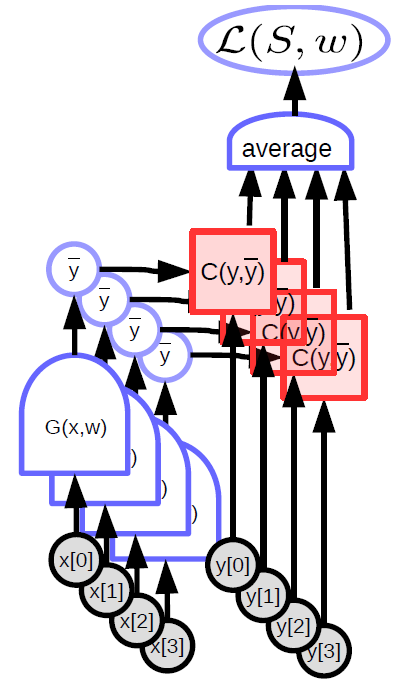
손실 함수는 학습 과정 동안 최소화되어야 할 함수를 말한다. 여기에는 두가지의 손실이 있다:

1) 샘플당 손실 - \(L(x,y,w) = C(y, G(x,w))\) 2) 평균 손실 -

​ 어떤 샘플들로 구성된 집합 \(S = \lbrace(x[p],y[p]) \mid p \in \lbrace 0, \cdots, P-1 \rbrace \rbrace\) 가 있을 때,

​ 집합 $S$에 대한 평균 손실은 다음과 같이 주어진다. : \(L(S,w) = \frac{1}{P} \sum_{(x,y)} L(x,y,w)\)

그림 2: 평균 손실에 기반한 모델의 연산 그래프

일반적인 지도 학습에서는, (샘플당) 손실은 단순하게 손실 함수의 출력으로 표현할 수 있다. 기계 학습에서는 대부분 최적화해야 할 함수로 표현한다.(일반적으로는 이 함수를 최적화해야 한다.) 또한 GAN에서처럼 두 함수간의 내시 균형^{Nash Equilibria}을 찾는 것과 연관되어 있기도 한다. 이런 작업은 경사 기반의 방법들을 통해서 수행할 수 있지만, 이것이 꼭 경사하강법일 필요는 없다.

경사 하강

경사 기반의 방법은 함수의 최소점을 찾는 방법/알고리즘이며, 이때 해당 함수의 경사를 쉽게 구할 수 있을 것라는 전제를 둔다. 이 전제는 함수가 거의 모든 구간에서 연속적이고, 미분가능하다는 것을 포함하고 있다. (꼭 모든 구간에서 미분가능할 필요는 없다.)

직관적인 경사 하강법 - 안개가 짙게 낀 한밤중의 산에 있다고 가정해보자. 당신은 마을로 내려가길 원하지만, 한정된 시야각을 가지고 있기 때문에, 가장 가파르게 경사가 하강하는 방향을 찾기 위해서 당신 부근을 살펴 볼 것이고, 그 방향으로 한 발자국 나아갈 것이다.

경사 하강의 다른 방법들

• 완전 (배치) 경사 하강법에서의 업데이트 :

  \[w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\]

• SGD (확률적 경사 기반)에서는 업데이트가 다음과 같이 바뀐다.:

  • $p \in \lbrace 0, \cdots, P-1 \rbrace$ 를 선택하고, 다음과 같이 업데이트한다.

    \[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

여기서 ${w}$ 는 최적화해야 할 매개변수를 나타낸다.

$\eta$ 는 위 식에서는 상수로 정의되어 있지만, 조금더 복잡한 알고리즘에서는 행렬로 정의될 수도 있다$.

만약 이 행렬이 양의 준정부호 행렬^{positive semi-definite matrix}라면, 우리는 감소하는 방향으로 움직이긴 하나, 꼭 가장 가파르게 하강하는 방향으로 움직일 필요는 없다. 실제로 가장 가파르게 하강하는 방향이 항상 우리가 움직이기를 원하는 방향을 지향하는 것은 아니다.

만약 함수가 미분 가능하지 않다면, 다시 말해, 구멍이 나 있거나 계단처럼 층이 져 있다던가 평평해서 경사 값이 아무런 정보도 주지 못하는 경우에는, 0차 방법 또는 경사를 이용하지 않는 방법^{Gradient-Free Methods}라고 불리는 다른 방법들을 적용해야 한다. 딥러닝에서는 모두 경사 기반의 방법들에 대해서만 다루고 있다.

하지만, RL (강화 학습)에서는 경사에 대한 명확한 형태 없이 경사를 추측하는 방법이 관련되어 있다. 한가지 예를 들자면, 로봇이 매번 넘어지는 것을 통해서 자전거를 타는 방법을 학습하는 것을 들 수 있다. 이 때 목적 함수는 자전거를 얼마나 넘어지지 않고 오래 타는지를 통해서 계산할 수 있다. 하지만, 여기서는 목적 함수에 대한 경사를 구할 수 없다. 로봇은 뭔가 다른 방법을 시도해보아야 한다.

RL에서의 비용 학습는 대부분의 시간동안 미분가능하지 않지만, 출력을 계산하는 신경망은 경사 기반의 방법을 취하고 있다. 이 것이 바로 지도 학습과 강화 학습간의 핵심 차이이다. 후자의 경우에서, 비용 함수 $C$는 미분 가능하지 않다. 실제롤 이 함수를 전혀 알지 못한다. 마치 블랙박스처럼 입력을 넣었을 때, 단순하게 출력만 돌려준다. 이러한 방법은 매우 비효율적이며, RL의 단점 중 하나인데, 구체적으로 말하자면 매개변수 벡터가 고차원을 가지는 것을 말한다. (이 말은 우리가 탐색해야할 정답의 영역이 매우 넣고, 결국 어디로 움직여야 할지 찾는게 어렵다는 것을 의미한다.)

RL에서 가장 유명한 방법이 Actor Critic 방법이다. Critic 방법은 기본적으로 알고 있고, 학습이 가능한 두번째 비용 함수 모듈을 포함하고 있다. 하나는 미분가능한 비용 함수 모듈을 학습시킬 수 있는데, 이를 이용해서 비용 함수/보상 함수를 근사하게 된다. 보상은 마치 벌칙을 주는 것처럼 음의 값을 가지고 있다. 이렇게 하는 것이 비용 함수를 미분가능하게 만드는 방법이거나, 적어도 미분가능한 함수로 근사함으로써 이를 역전파 알고리즘에 적용시킬 수 있게 해준다.

전통적인 신경망 구조에서 SGD와 역전파 알고리즘의 이점

확률적 경사 하강법 (SGD)의 이점

실제로 적용할 때, 우리는 매개변수에 관한 목적함수의 기울기를 계산할 때, 경사 하강법을 사용한다. 전체 샘플에 대한 평균을 통해서 목적함수의 전제 경사를 계산하는 것 대신에, 확률적 경사 하강법은 딱 하나의 샘플을 취하고, 이에 대한 손실 $L$ 를 계산하고, 매개변수에 대한 손실의 기울기를 구한 후, 해당 기울기 방향의 반대로 한 걸음 나아간다.

공식에서는, $w$ 가 $w$에 주어진 샘플에 대한 매개변수 ($x[p]$,$y[p]$) 를 활용하여 구한 샘플당 손실 함수의 기울기를 곱한 값을 빼주는 방향으로 접근한다.

이렇게 단일 샘플에 대해서 해당 방법을 적용한다면, 그림 3에서 보여지는 것처럼 매우 오차가 심한 경로가 나올 것이다. 이렇게, 손실이 바로 감소하지 않고, 확률적으로 나타나게 된다. 매 샘플은 손실을 서로 다른 방향으로 유도하게 된다. 단순히 평균이 최소화되는 방향으로 이끄는 평균이 된다. 비록 이 방법이 비효율적으로 보일지 모르겠지만, 적어도 샘플이 약간의 반복성을 나타내는 머신 러닝 관점에서는 배치 경사 하강법보다는 빠르게 동작한다.

그림 3: 매 샘플을 업데이트 할 때의 확률적 경사 하강법의 경로

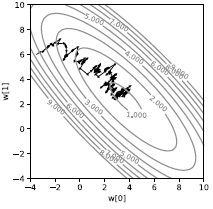실제로, 단일 샘플 상에서는 확률적 경사 하강법 대신에 배치를 사용한다. 그래서 단일 샘플이 아닌, 샘플들의 배치에 대해서 기울기의 평균값을 계산하고, 다음 단계를 진행한다. 이렇게 하는 이유는 보통 배치를 사용할 경우, 병렬화하기 쉽기 때문에 (GPU나 멀티코어 CPU와 같은) 주어진 하드웨어를 효율적으로 사용할 수 있게 된다. 배치로 나누는 것은 병렬화할 수 있는 가장 간단한 방법이다.

과거의 신경망

과거의 신경망은 기본적으로 선형 연산과 부분적으로 비선형 연산을 하는 계층들이 산재되어 있는 형태로 되어 있다. 선형 연산이란, 개념적으로 간단하게 행렬-벡터 곱셈을 나타낸다. (입력) 벡터를 받아서 가중치로 구성된 행렬을 곱하게 된다. 두번째 연산은 이렇게 가중치를 가한 벡터의 요소들을 ($\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$ 등과 같이) 간단한 비선형 항수에 넣는 것이다.

Figure 4: 과거의 신경망

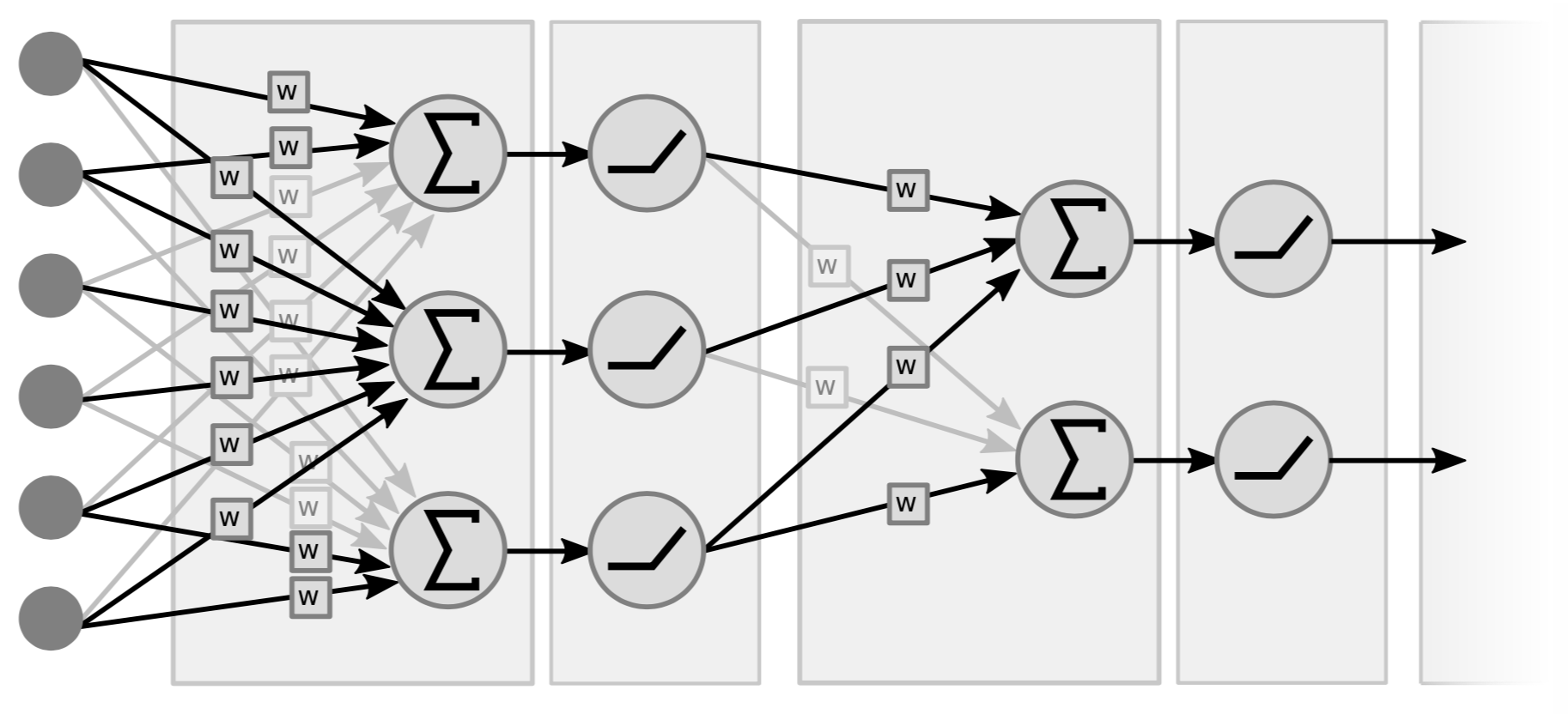그림 4는 2개의 계층으로 구성된 신경망의 예시인데, 이 계층들이 (선형+비선형과 같이) 쌍으로 구성되어 있다. 어떤 사람들은 변수도 고려하면서 3개의 계층으로 이뤄진 신경망이라고 표현하기도 한다. 참고할 점은 중간 계층에서 비선형성이 있지 않다면, 하나의 계층으로 표현할텐데, 이는 두 개의 선형 함수를 곱셈 연산을 하면 결국 선형 함수가 되기 때문이다.

그림 5는 신경망내에서 선형 계층과 비선형 계층이 어떻게 동작하는지를 보여준다.

그림 5: 선형 계층과 비선형 계층의 내부 구조

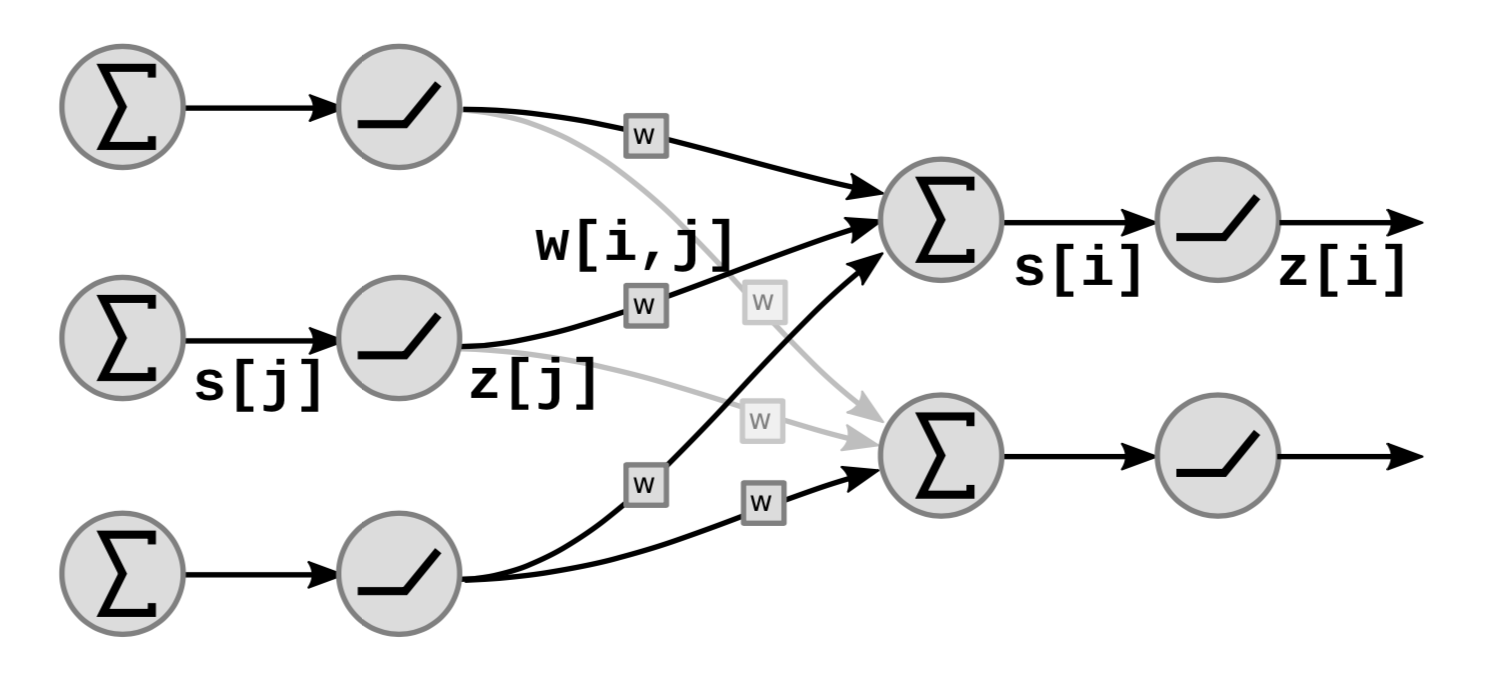그래프 내부를 보면, $s[i]$은 아래와 같이,

${i}$ 번째 요소까지 가중치를 가한 합을 나타내는데, 여기서 $UP(i)$ 은 $i$ 에 대한 선행 요소를 말하고, $z[j]$ 는 이전 계층에서의 $j$ 번째 출력을 말한다.

이때 출력 $z[i]$ 은 아래와 같이 계산할 수 있는데,

여기서 $f$ 는 비선형 함수를 말한다.

비선형 함수에 대한 역전파 알고리즘

역전파 알고리즘을 수행할 때 가장 처음 하는 일은 비선형 함수를 통해서 역전파 알고리즘을 수행하는 것이다. 신경망에서는 특정 비선형 함수 $h$를 선택하고, 이외의 나머지 요소는 내버려 둔다.

그림 6: 비선형 함수를 통한 역전파 알고리즘

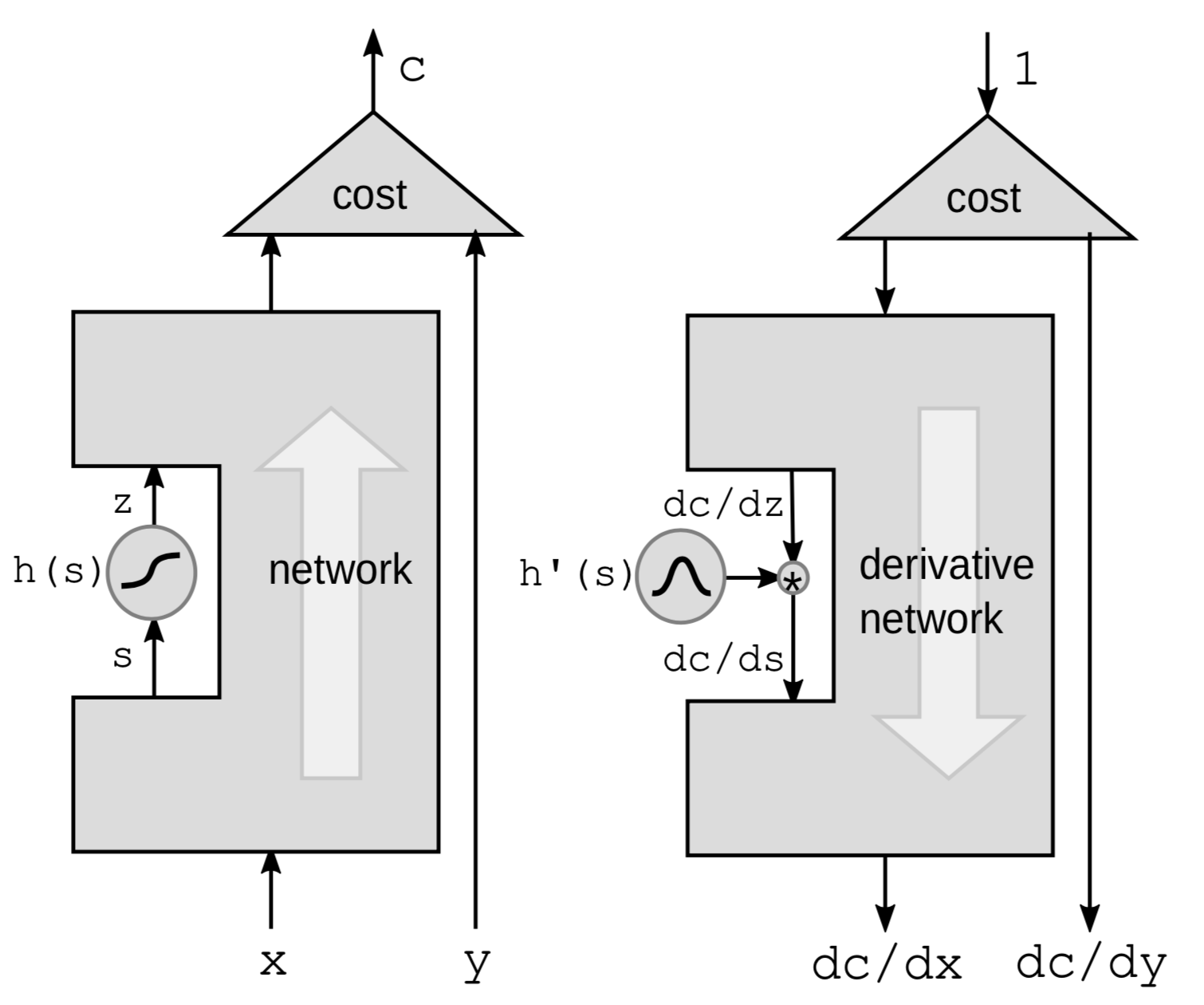여기서 경사를 계산할 때, 연쇄 법칙을 사용한다.

여기서 $h’(s)$ 는 $z$를 $s$에 관하여 미분한 값이고, $\frac{\mathrm{d}z}{\mathrm{d}s}$ 라고 표현할 수 있다. 미분항들간의 관계를 명확하게 하기 위하여, 위의 공식을 다시 써볼 수 있다.

게다가 신경망내에 이런 함수들이 연쇄적으로 놓여있다면, 모든 ${h}$ 함수에 대한 미분을 한번에 구해서 곱하는 것으로 역전파 알고리즘을 수행할 수 있다.

변화량에 대해서 이를 생각해본다면, 조금더 직관적으로 이해할 수 있다. $\mathrm{d}s$ 에 대한 변화량은 $z$ 에 대한 것으로 아래와 같이 정의할 수 있다.

결국 이를 통해서 $C$에 대한 변화량으로 바꿔볼 수 있다.

다시 말하지만, 결국 위의 식으로 마무리 지을 수 있다.

가중합을 이용한 역전파 알고리즘

선형 계층에서는, 가중합을 통해서 역전파 알고리즘을 수행한다. 여기서 ${z}$ 변수로부터 연결된 $s$ 변수들을 제외하고 나머지 신경망에 대해서는 블랙박스로 생각해본다.

그림 7: 가중합을 이용한 역전파 알고리즘

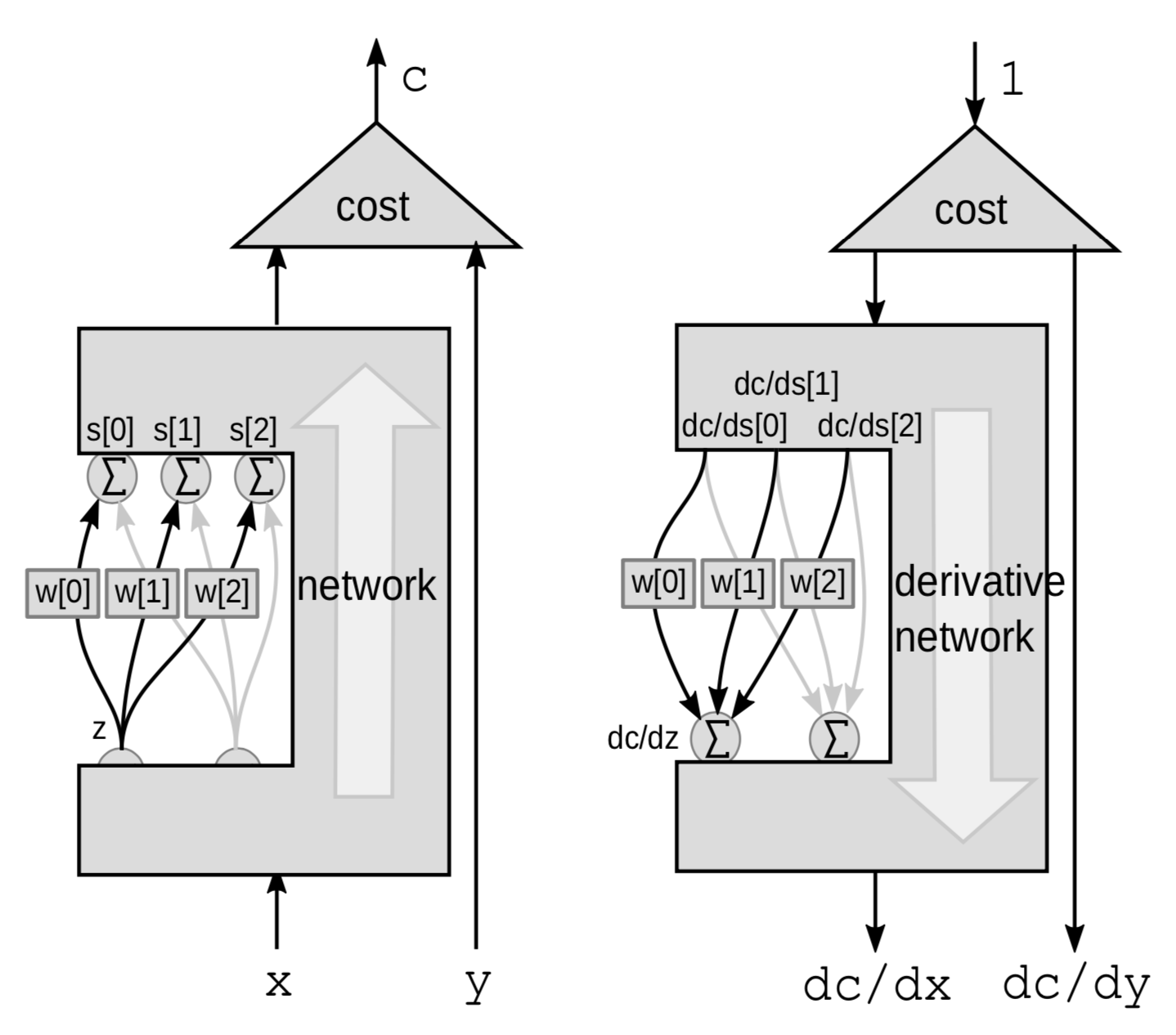이번에는 가중합이 변화량이 된다. $Z$는 여러 변수에 영향을 미치게 되는데, $\mathrm{d}z$ 를 통해서 $z$에 대한 변화량을 구하면, $s[0]$, $s[1]$ 그리고 $s[2]$에 대한 변화량도 아래와 같이 계산되고

이런 과정을 통해서 $C$에 대한 변화량도 구하게 된다.

더불어 $C$도 3개의 형태들에 대한 합으로 나눠서 볼 수 있게 된다:

신경망과 일반적인 역전파 알고리즘을 PyTorch로 구현하는 방법

과거의 신경망에 대한 구성도

• 선향 계층 $s_{k+1}=w_kz_k$

• 비선형 계층 $z_k=h(s_k)$

  

$w_k$: 행렬 $z_k$: 벡터 $h$: 스칼라 ${h}$ 함수를 모든 요소에 적용할 수 있게 바꾼 것이다. 이건 선형 함수와 비선형 함수의 짝으로 되어 3개의 계층으로 이뤄진 신경망인데, 사실 최근에 나오고 있는 신경망은 선형 연산과 비선형 연산, 그리고 좀 더 복잡한 연산에 대해서 명확하게 구분을 하지 않는다.

PyTorch 구현

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # 입력 Tensor를 1차원 아래로 펴줌
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

PyTorch를 이용하면, 객체 지향적 클래스를 이용한 신경망을 구현할 수 있다. 우선, 신경망에 대한 클래스를 정의하고, 미리 정의된 nn.Linear 클래스를 이용해서 선형 계층을 초기화할 수 있다. 선형 계층은 스스로 매개변수 벡터를 포함하고 있기 때문에 분리된 객체로 존재해야 한다. nn.Linear 클래스는 내부적으로 편향 벡터를 더하기도 한다. 그러고 난 후에 비선형 활성 함수로써 $\text{torch.relu}$ 함수를 이용해서 출력을 계산할 수 있는 forward 함수를 정의한다. relu 함수는 매개변수를 가지지 않기 때문에 초기화할 필요는 없다.

• PyTorch가 자체적으로 역전파 알고리즘을 수행하고, forward 함수에 대한 경사를 계산하기 때문에, 우리 스스로 경사를 계산할 필요는 없다.

functional 모듈을 통한 역전파 수행

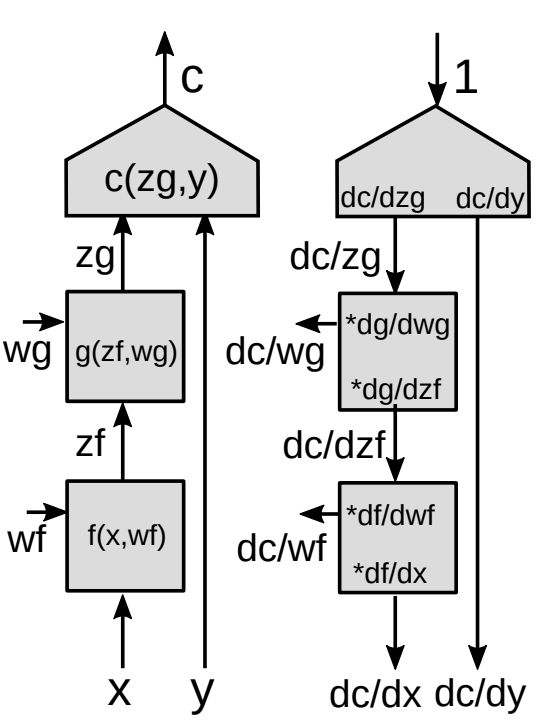
여기서 이제 역전파 수행의 일반화된 형태에 대해서 소개할 것이다. |

• 벡터 함수에 대해서 연쇄 법칙을 사용하면 아래와 같이 전개된다.

  \[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

  위 식은 연쇄 법칙을 사용해서 $\frac{\partial c}{\partial{z_f}}$ 을 구하는 기본적인 공식이다. 참고할 점은 스칼라 함수에 대한 경사를 벡터로 나타내면, 미분하기 원하는 요소에 대한 벡터와 같은 크기를 가진 것이 된다는 것이다. 표현 형식에 대한 일관성을 유지하기 위해서 열 벡터 대신에 행 벡터로 표현할 것이다.

• 야코비안 행렬

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

  $z_g$에 대해서 기회 비용이 주어졌을때, $z_f$에 대한 기회 비용의 기울기를 계산하기 위해서는 $\frac{\partial {z_g}}{\partial {z_f}}$ (야코비안 행렬 요소)가 필요하다. 각 요소 $ij$는 입력 벡터의 $j$번째 요소에 대해서 출력 벡터의 $i$번째 요소에 대한 부분 미분값을 나타낸다.

  만약 모듈이 층층이 쌓여있는 형태로 되어 있다면, 모든 모듈에 대한 야코비안 행렬을 곱하다 보면, 모든 내부 변수에 대한 경사를 구할 수 있게 된다.

다중 계층 그래프를 통한 역전파 전개

그림 9에 주어져 있는 것처럼, 신경망안에 여러 모듈들이 층층이 쌓여있는 형태를 고려해 보자.

그림 9: 다중 계층 그래프를 통한 역전파 전개

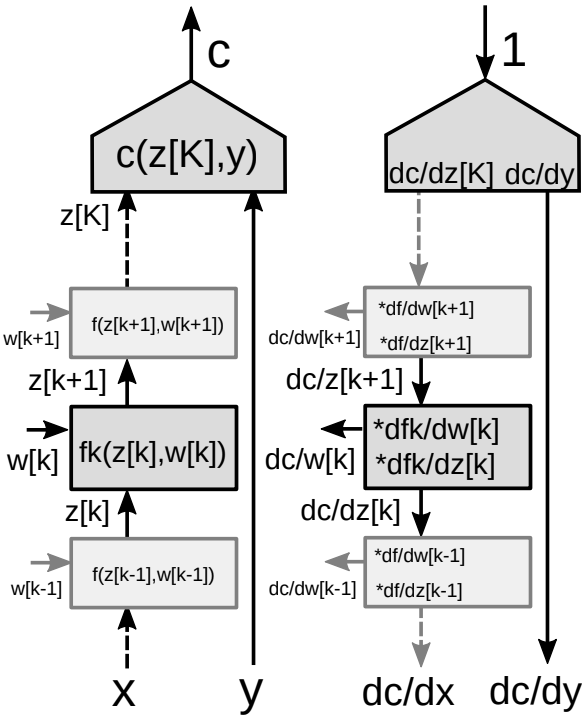역전파 알고리즘에서는 두가지 형태의 경사값이 필요한데, - 하나는 (신경망의 각 모듈별) 상태에 대한 경사이며, 다른 하나는 (특정 모듈의 모든 매개변수들) 가중치에 대한 경사이다. 그래서 결국 각 모듈이 연관되어 있는 두개의 야코비안 행렬이 필요하다. 역전파 수행을 위해서 연쇄 법칙을 다시 사용해볼 수 있다.

• 벡터 함수에 대한 연쇄 법칙을 사용하면 아래와 같다.

  \[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• 모듈에 대한 두개의 야코비안 행렬
  • $z[k]$에 관한 야코비안 행렬
  • $w[k]$에 관한 야코비안 행렬