선형대수학 및 데이터 시각화

자료

트위터에서 알프레도 칸지아니 (@alfcnz) 를 팔로우하세요. 선형대수학과 특이값 분해^{Singular Value Decomposition (SVD)}를 다룬 영상들과 교과서는 트위터에서 검색할 수 있습니다. (예시: linear algebra (from:alfcnz))

변환

동기부여를 위해 이미지 분류 예시로 시작하자. 우리가 1 메가픽셀 카메라로 사진을 찍었다고 가정하자. 이 이미지는 약 1,000 화소의 높이와 1,000 화소의 너비를 가지고, 각 화소는 빨간색, 녹색, 파란색(RGB)의 세 가지 색 치수를 갖게 된다. 그렇다면 각각의 사진은 300만차원 공간에서 하나의 점으로 간주될 수 있다. 이렇게 거대한 차원수를 지닌 공간에서, 우리가 분류하고 싶은 많은 흥미로운 이미지들 - (예를 들어 개와 고양이)은 공간 안에서 거의 같은 영역에 있을 것이다.

이러한 이미지를 효과적으로 분리하기 위해, 우리는 이러한 점들을 이동시키기 위해 데이터를 변환하는 방법을 고려한다. 기억할 점은, 2차원 공간에서 선형 변환은 행렬 곱셈과 동일하다는 것이다. 예를 들어, 다음은 선형 변환이다.

• 회전 (행렬이 직교행렬일 시).
• 크기 조정 (행렬이 대각행렬일 시).
• 박사 (행렬식이 음수일 때).
• 깎기.

주목해야 할 것은, 강체 변환을 하면 0이 항상 0으로 매핑되지 않기 때문에, 이는 선형 변환이 아니고 아핀 변환이다. 다시 우리 예제로 돌아가서, 우리는 데이터 포인트를 변환하여 점들이 0 주위에 군집되도록 바꾸고, 대각선 행렬로 크기 조정을 함으로써 우리가 그 지역을 “확대”해서 볼 수 있도록 할 수 있다. 마지막으로, 우리는 종류가 다른 점들을 나누는 선을 발견함으로써 분류를 할 수 있다. 즉, 선형 변환과 비선형 변환을 사용하여 점을 선형적으로 분리할 수 있는 공간으로 매핑하는 것이다. 이 아이디어는 다음 섹션에서 더 자세히 다룰 것이다.

데이터 시각화 - 네트워크를 사용하여 색상별로 점 구분하기

아래의 데이터 시각화에는 각기 다른 색을 가진 다섯 부분으로 나누어진 나선이 있다. 점들은 2차원 평면에 존재하며, 투플^tuple로 나타낼 수 있고, 점들의 색은 각 점들의 종류를 나타내는 세 번째 차원을 나타낸다. 그 후 우리는 신경망을 사용하여 각각의 점들을 색상별로 구분한다.

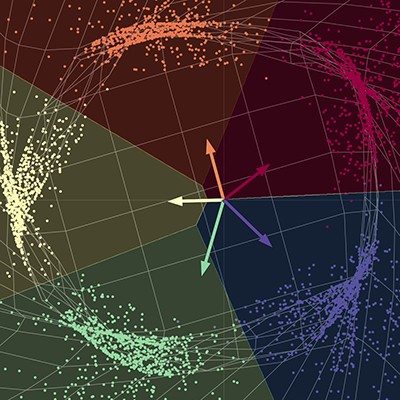(a) 입력되는 점들, 신경망 통과 전	(b) 출력된 점들, 신경망 통과 후

신경망은 각각의 점을 서로 다른 부분 공간으로 분리하기 위해 공간을 "잡아당긴다". 수렴 시에, 신경망은 각각의 색을 최종 다양체의 각기 다른 부분 공간으로 분리한다. 다시 말해서, 이 새로운 공간에 있는 각각의 색은 회귀 분석을 사용하여 다른 모든 색들로부터 선형적으로 분리될 수 있을 것이다. 그림에 보이는 벡터들은 5x2 행렬로 나타낼 수 있고, 각 점들에 이 행렬을 곱함으로써 각 색에 대한 점수를 얻을 수 있다. 그 후 각각의 점들을 그들의 색상 점수를 사용하여 색상별로 분류할 수 있다. 여기서 출력 차원수는 색상별로 하나씩 해서 5이며, 입력 차원수는 x와 y 좌표 하나씩 해서 2이다. 요약하자면, 이 신경망은 여러 행렬과 비선형성을 통해 공간을 변환한다.

신경망 구조

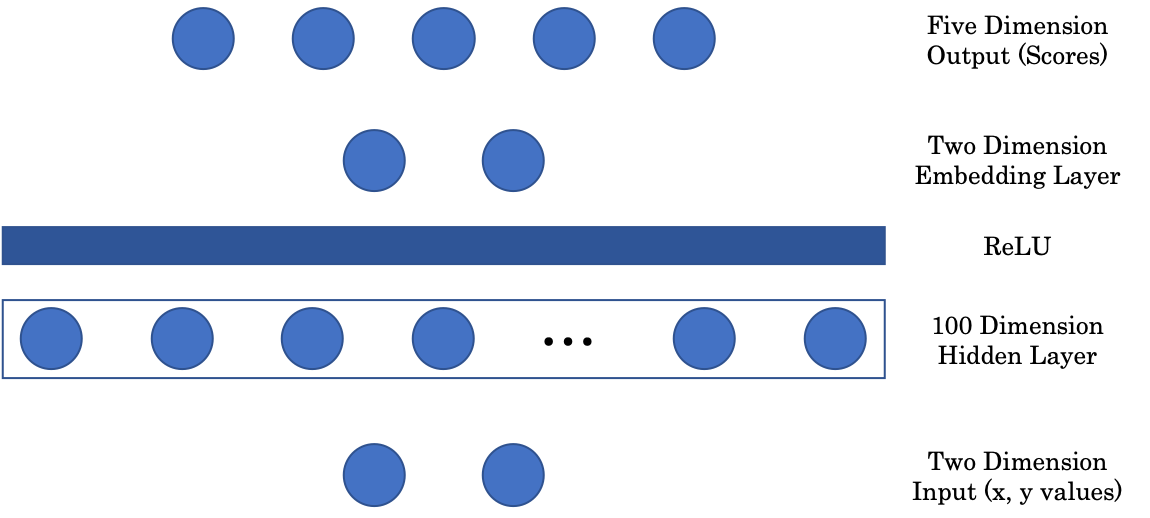
그림 2: 신경망 구조

첫 번째 행렬은 2차원의 벡터를 입력받아 100차원의 은닉층에 매핑한다. 그런 다음 양수 부분만을 가져오는 $(\cdot)^+$ ReLU 또는 Rectified Linear Unit 이라는 비선형 함수를 통과한다. 다음으로, 우리의 이미지를 시각화하기 위해, 100차원의 은닉층 입력을 2차원 출력에 매핑하는 임베딩 계층을 포함한다. 마지막으로 임베딩 계층은 각 색상별 점수를 나타내는 신경망의 마지막에 있는 5차원 계층에 투영된다.

무작위 투영 - 주피터 노트북

주피터 노트북은 여기서 찾을 수 있다. 노트북을 실행하려면 README.md에 지정된 대로 pDL 환경이 설치되어 있어야 한다.

파이토치 device

파이토치는 컴퓨터의 CPU와 GPU 모두에서 실행될 수 있다. CPU는 순차적인 작업에 유용하고, GPU는 병렬적인 작업에 유용하다. 원하는 장치에서 실행하기 전에 먼저 텐서와 모델이 해당 장치의 메모리로 전송되었는지 확인해야 한다. 이는 다음 두 줄의 코드로 할 수 있다.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)

첫 줄은 device라는 변수를 만드는데, 사용가능한 GPU가 있다면 GPU 장치가 되고, 그렇지 않으면 CPU로 기본 설정된다. 다음 줄에서는 텐서를 생성한 후 .to(device) 를 통해 해당 텐서를 장치의 메모리에 보낸다.

주피터 노트북 팁

노트북 셀의 기능에 대한 설명서를 보려면 ‘Shift + Tab’ 단축키를 사용하시오.

선형 변환 시각화

선형 변환을 행렬로 나타낼 수 있다는 점을 기억하자. 특이값 분해를 사용하여 이 행렬을 각각 다른 선형 변환을 나타내는 세 개의 행렬로 분해할 수 있다.

수식 1 의 행렬 $U$ 와 $V^\top$ 은 직교 행렬이며 and 각각 회전 변환과 반사 변환을 가르킨다. 중간에 있는 행렬은 대각선 행렬이며, 크기 조정을 담당한다.

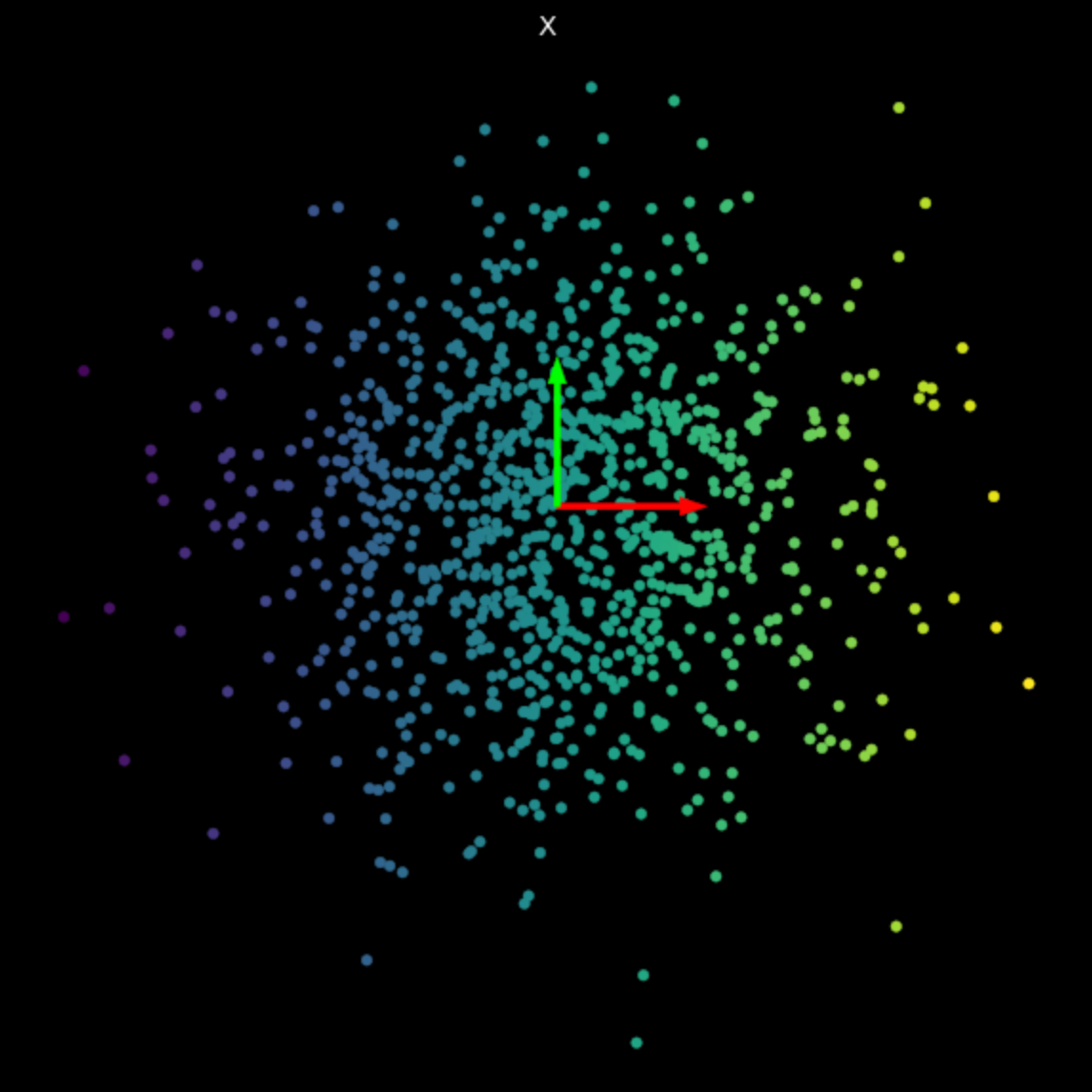
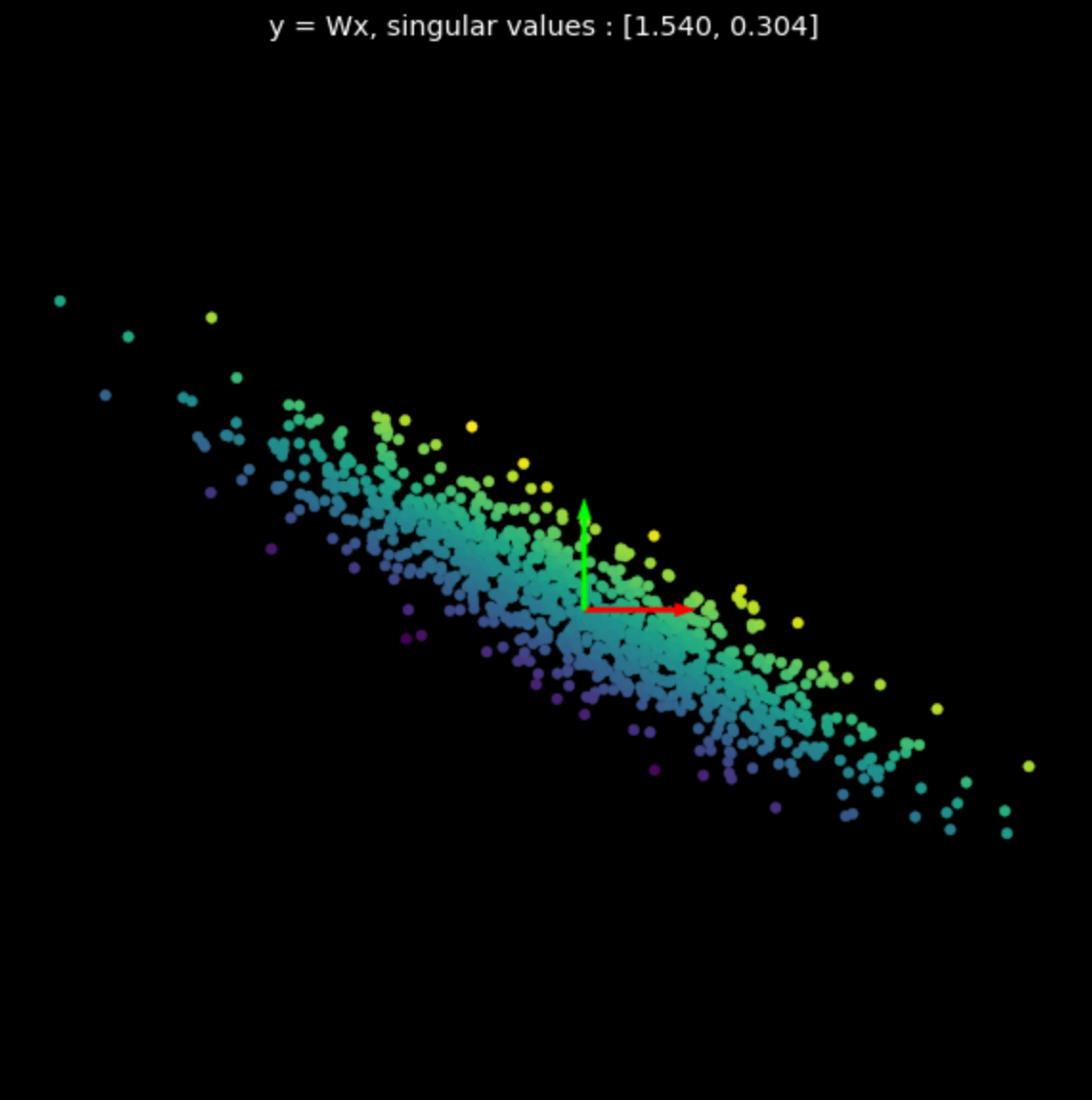
그림 3에는 여러 무작위 행렬들의 선형 변환을 시각화되어 있다. 특이값들이 변환의 최종 결과에 주는 영향을 확인해보자.

이 시각화에 사용된 행렬들은 넘파이로 생성되었다. 그러나, 파이토치로도 ‘nn.Linear’ 에 ‘bias = False` 옵션을 성정해서 선형 변환을 만들 수 있다.

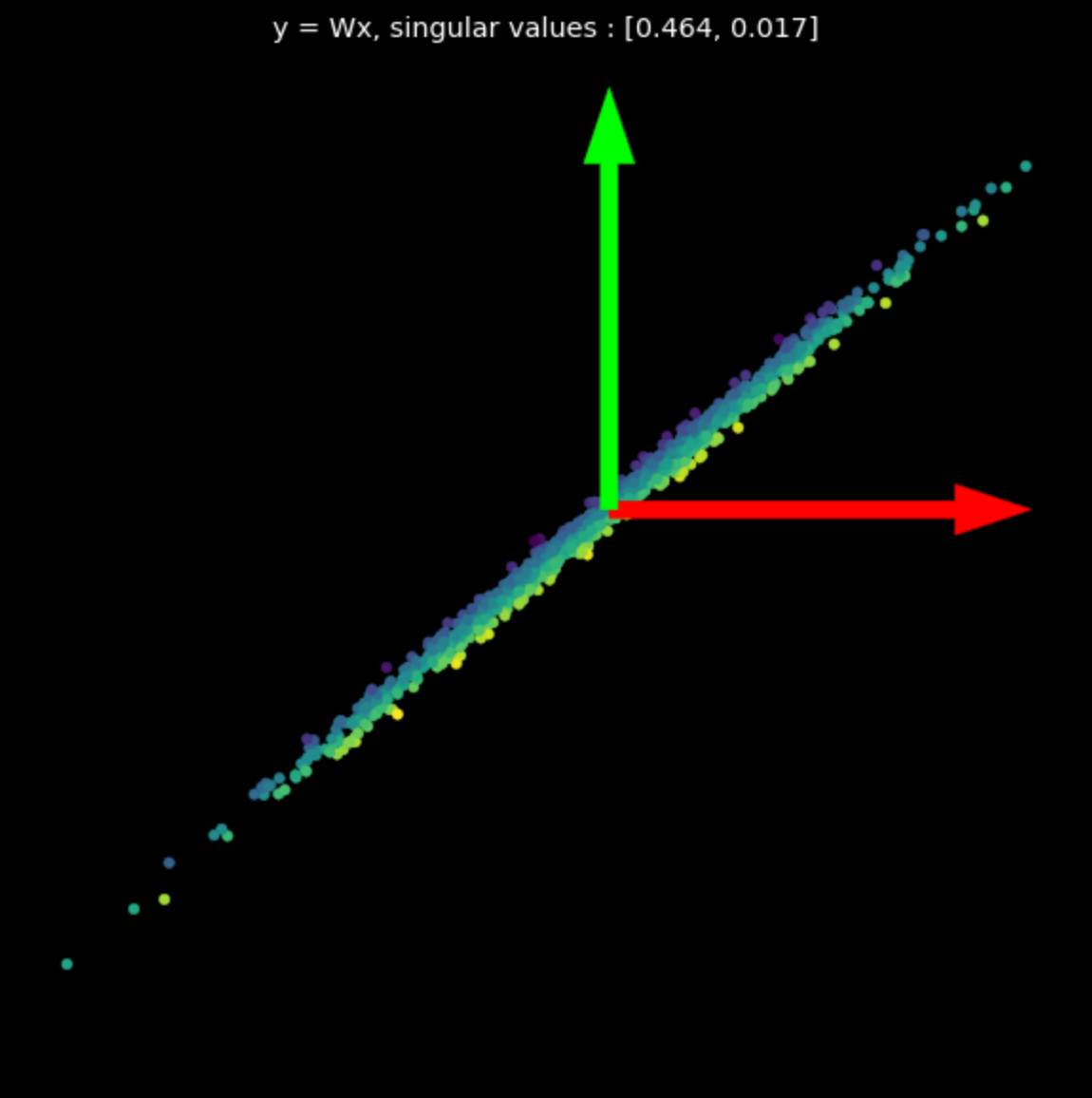(a) 원본	(b) $s_1$ = 1.540, $s_2$ = 0.304	(c) $s_1$ = 0.464, $s_2$ = 0.017

비선형 변환

다음과 같은 변환을 시각화해보자.

그림 4에 있는 $\tanh(\cdot)$ 그래프를 기억하자.

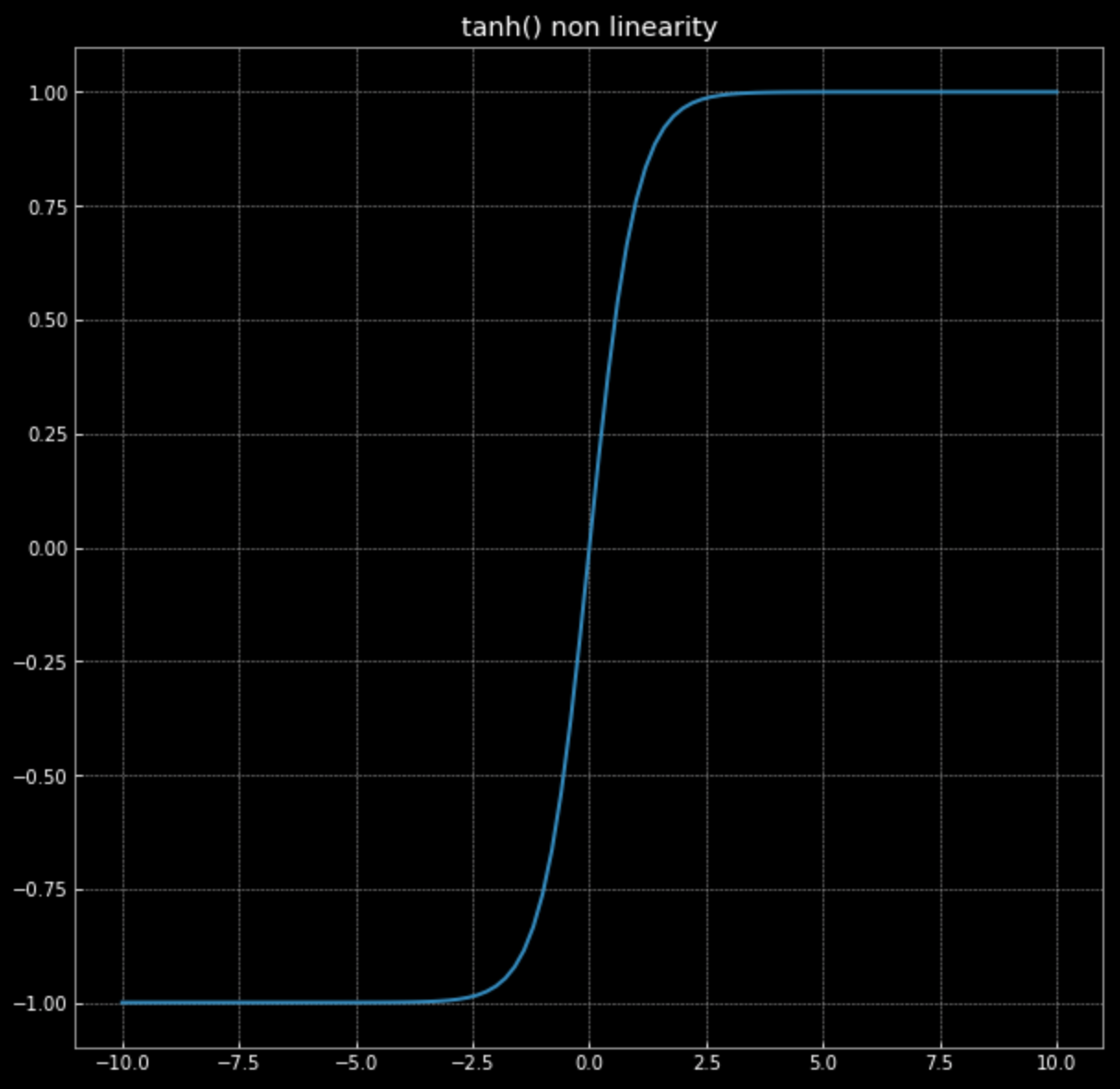
그림 4: 쌍곡탄젠트 비선형변환

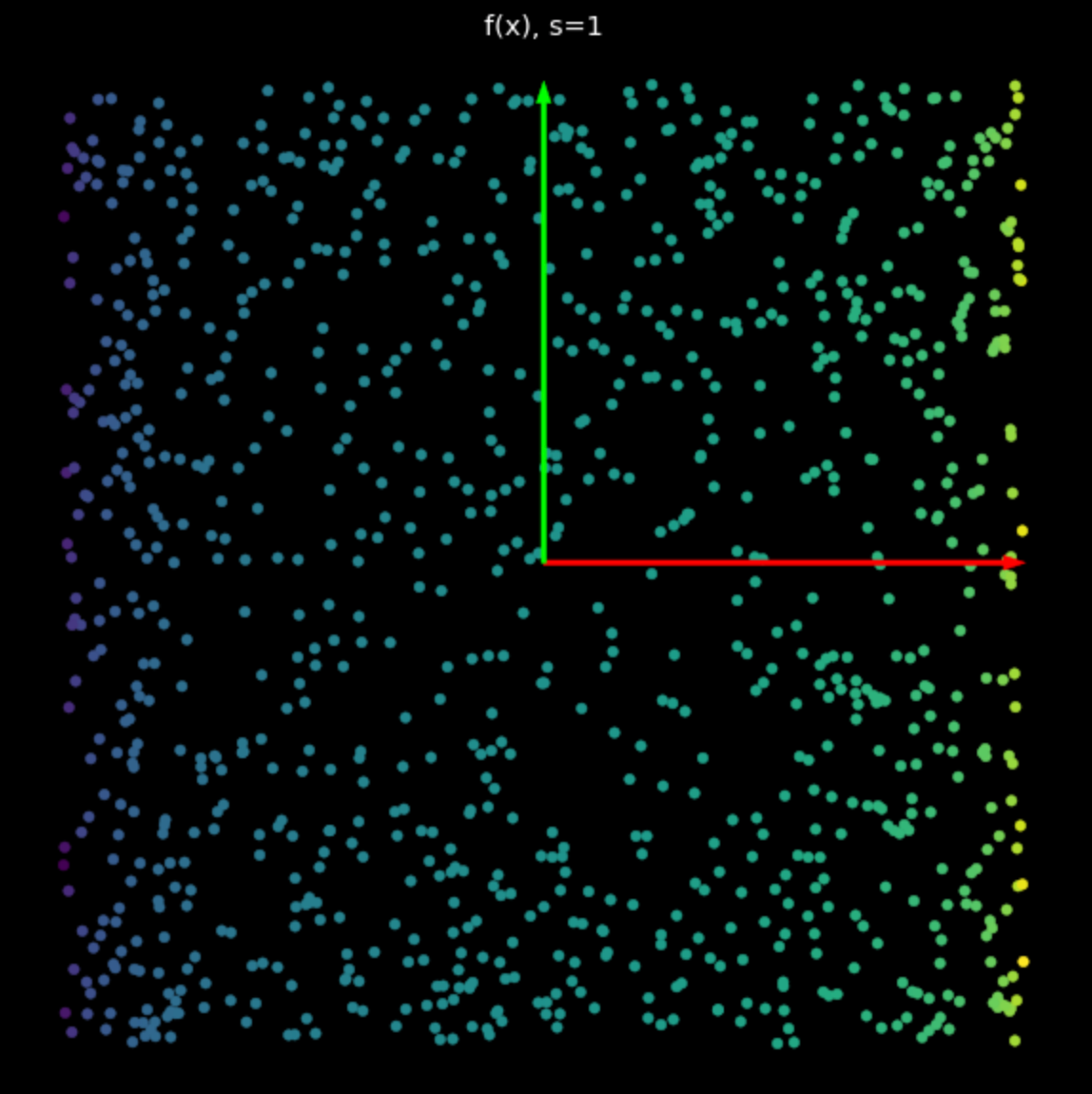
이 비선형 변환의 효과는 점들을 $-1$과 $+1$ 사이로 가두어 정사각형을 만드는 것이다. 수식 2에서 $s$가 증가함에 따라, 점점 더 많은 점들이 이 정사각형의 가장자리로 밀리게 된다. 이것은 그림 5에 나타나 있다. 가장자리에 더 많은 점을 보내면서, 우리는 이 점들을 더 넓게 펼치고 이들을 분류하려고 시도할 수 있다.

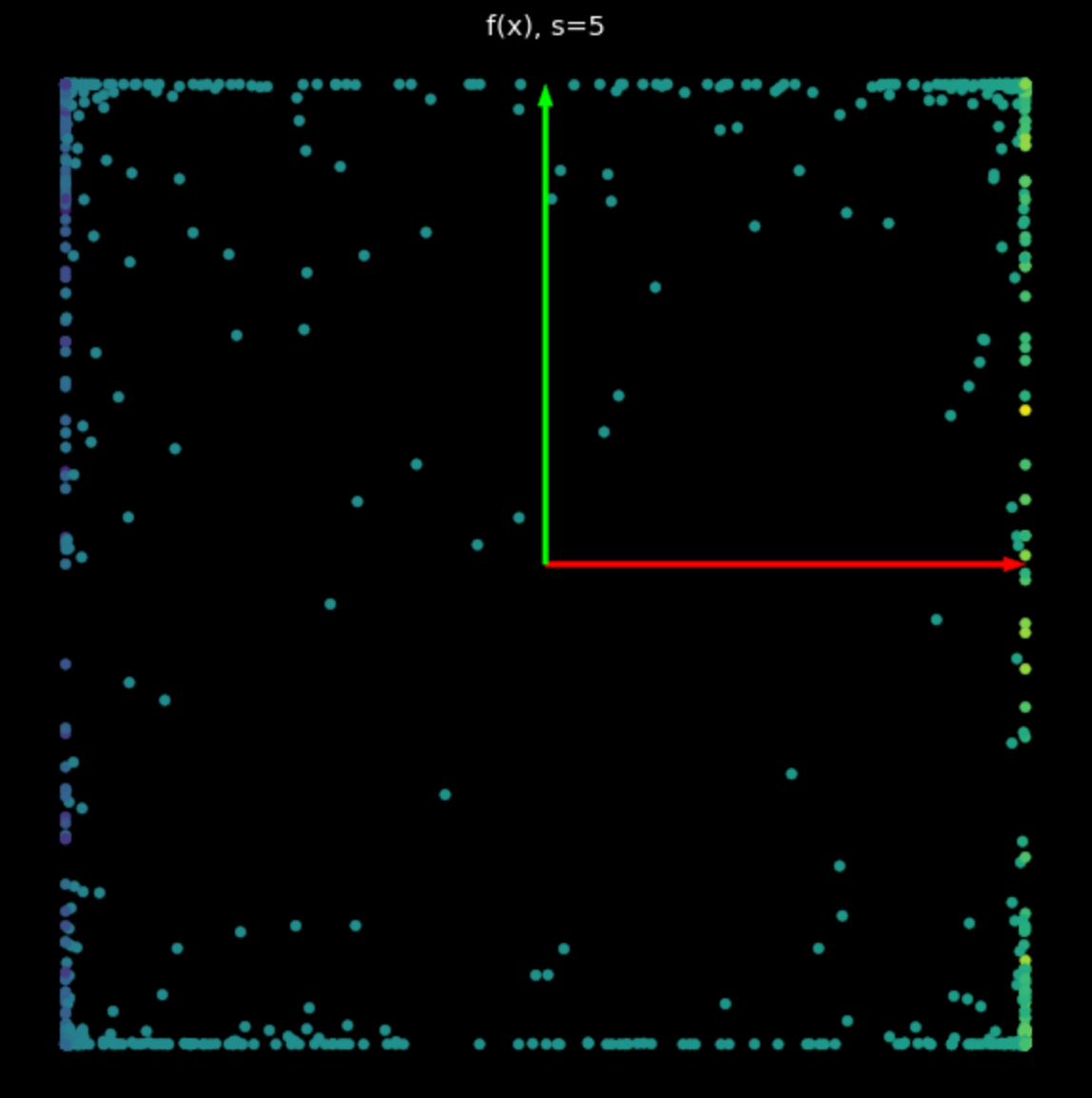(a) $s=1$ 일 때 비선형변환	(b) $s=5$ 일 때 비선형변환

무작위 신경망

마지막으로, 학습되지 않은 간단한 신경망의 변환을 시각화해보자. 신경망은 아핀 변환을 수행하는 선형 레이어, 쌍곡탄젠트 비선형 변환, 그리고 다시 선형 레이어로 이루어져 있다. 그림 6에서 변환 결과를 살펴보면 앞에서 본 선형 및 비선형 변환과는 다르다는 것을 알 수 있다. 앞으로, 우리는 신경망에 의한 변환들을 분류라는 최종 목표에 유용하게 만드는 방법을 볼 것이다.

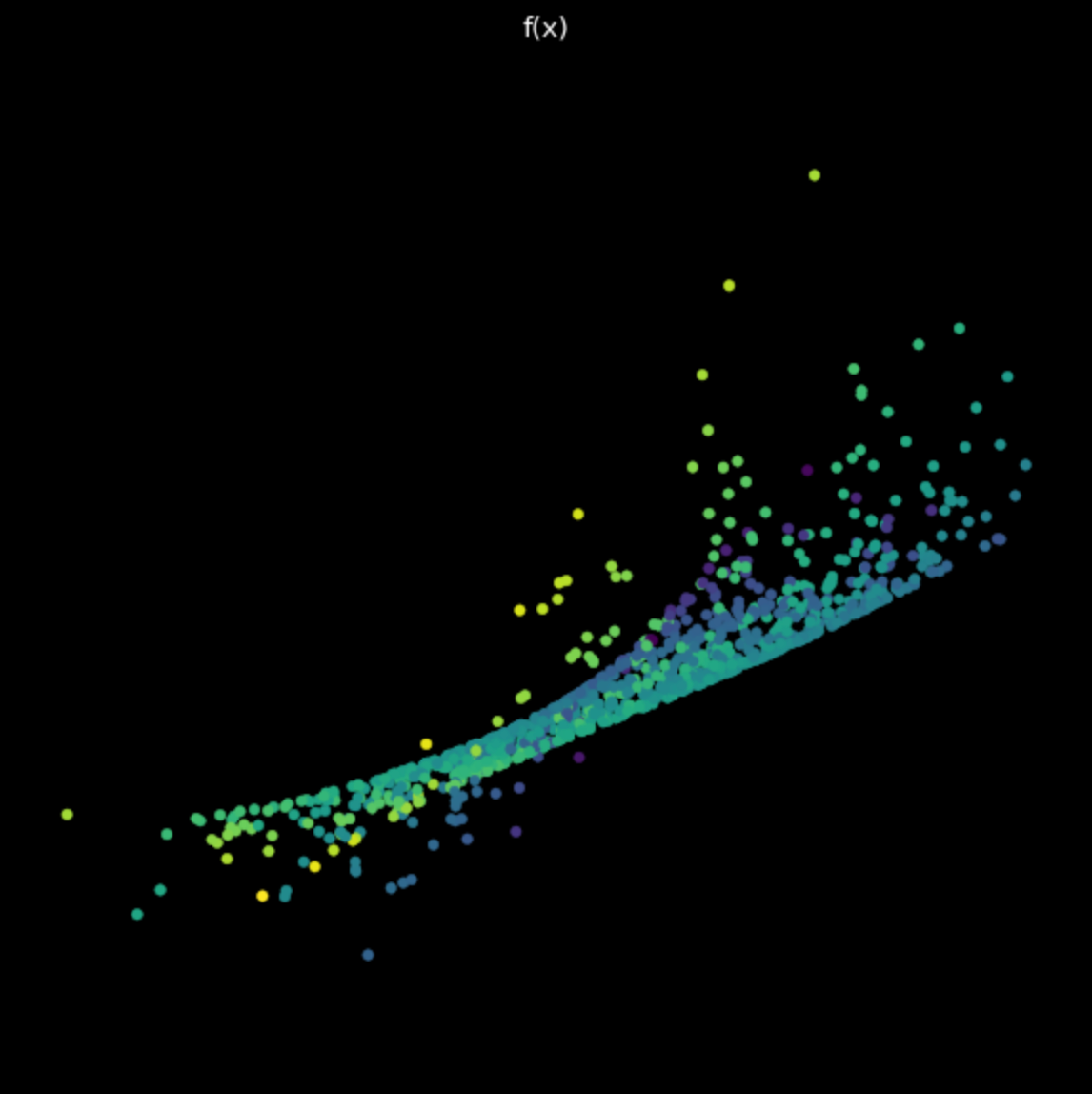
그림 6: 학습되지 않은 신경망의 변환