Méthodes d'enchâssements joints régularisées

Méthodes non contrastives

Méthodes non contrastives et théorie de l’information

La plupart des méthodes non contrastives sont basées sur la théorie de l’information. Par exemple la réduction de la redondance (Barlow Twins) et de l’information. Elles ne nécessitent pas d’architectures spéciales ou de techniques d’ingénierie.

VicReg

La méthode essaie de maximiser le contenu informationnel des enchâssements en produisant des variables d’enchâssement qui sont décorrélées les unes des autres. Si les variables sont corrélées les unes aux autres, elles covarient ensemble et le contenu informationnel est réduit. Ainsi, cette méthode empêche un effondrement informationnel dans lequel les variables portent des informations redondantes. De plus, cette méthode nécessite une taille de batch relativement faible.

Deux types d’effondrement peuvent se produire dans ces architectures :
$\textbf{Type 1}:$ Indépendamment de l’entrée, le réseau génère la même représentation.
$\textbf{Type 2}:$ Effondrement spécial où bien que des images différentes aient des représentations différentes, le contenu en information est vraiment faible dans chaque représentation.

Fonction de perte

La fonction de perte :

1. rapproche les paires positives afin d’être invariant à l’augmentation de données
2. rend la variance des enchâssements grande en poussant tous les termes diagonaux de la matrice de covariance afin d’empêcher le premier type d’effondrement.
3. rend la covariance des enchâssements faible en poussant tous les termes diagonaux de la matrice de covariance afin d’éviter le second type d’effondrement.

Méthodes de clustering

SwAV

Cette méthode empêche la solution triviale en quantifiant l’espace d’incorporation et fonctionne de la façon suivante :

1. On génère des représentations et on les empile (pour former $\green{H_{x}}$ et $\green{H_{y}}$).
2. On applique la méthode de clustering de l’algorithme de Sinkhorn à chacune des représentations empilées afin de générer les matrices $\green{\boldsymbol{Q}}$ correspondantes. Chaque ligne ($\violet{q_{\vx}}$) de ces matrices représente un vecteur one-hot indiquant le cluster auquel appartient la représentation correspondante.
3. On effectue un deuxième clustering pour les représentations $\vh_{\vx}$ et $\vh_{\vy}$ avec un soft-kmeans.
4. Cette étape génère à partir de $\vh_{\vx}$ des prédictions pour $\violet{\tilde{q_{\vx}}}$ et $\tilde{\violet{q_{\vy}}}$ et génère à partir de $\vh_{\vy}$ des prédictions pour $\green{q_{\vx}}$ et $\green{q_{\,\vy}}$. On parle alors de prédiction échangées (swap en anglais d’où le nom de la méthode).
5. On minimise la fonction de perte qui est la somme de deux fonctions d’entropie croisée entre $\green{q_{\vx}}$ et $\violet{\tilde{q_{\vx}}}$ et $\green{q_{\vy}}$ et $\violet{\tilde{q_{\vy}}}$.

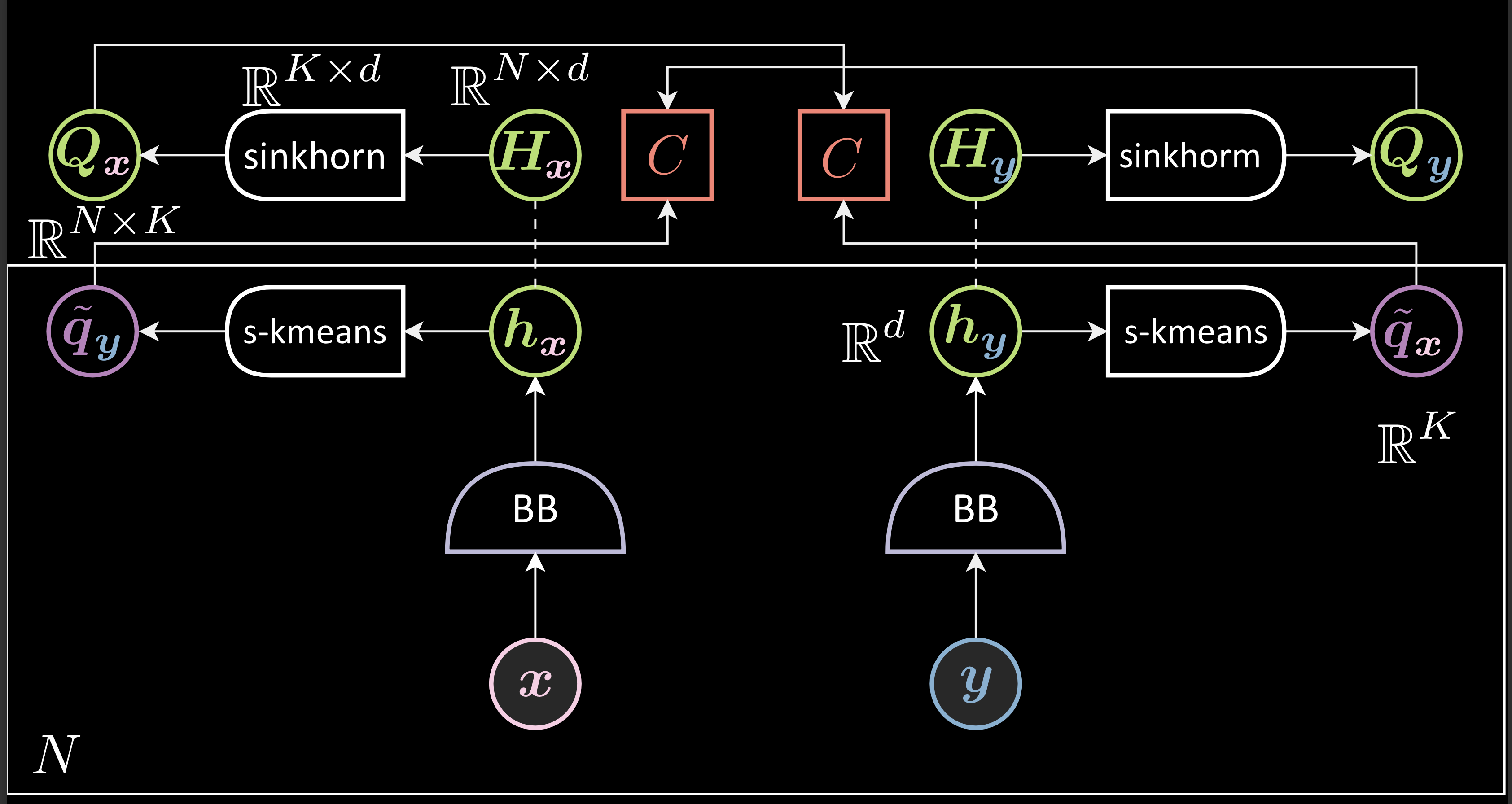
Figure 1 : SWaV

La fonction de perte

L’algorithme de Sinkhorn : L’algorithme de Sinkhorn permet de distribuer les échantillons non pas à un seul cluster mais à tous les clusters. Ainsi, il peut nous aider à éviter que toutes les données se regroupent en un seul centroïde ou toute autre distribution non uniforme. Il prend en compte des hyperparamètres qui nous permettent de déployer différents niveaux de distribution uniforme entre les clusters, revenant à équivaloir à l’algorithme K-means à un extrême et à la distribution uniforme à l’autre extrême.

Clustering softargmax : Chaque $\green{h_{\vy}}$ est normalisé. L’indice $\boldsymbol{W}\green{h_{\vy}}$ indique la similarité entre $\green{h_{\vy}}$ et tous les autres centroïdes. La fonction softargmax transforme la similarité cosinus (positif ou négatif) en une probabilité.

Comme il s’agit de prédire $\green{q_{\vx}}$, nous allons comparer l’entropie croisée de la prédiction, $\violet{\tilde{q_{\vx}}$, avec le $\green{q_{\vx}}$ réel.

Interprétation des clusters

Cette méthode partitionne automatiquement l’espace latent en quelques clusters sans étiquettes et notre espoir est que ces clusters seront liés aux classes réelles. Ainsi, plus tard, nous n’aurons besoin que de quelques échantillons de données étiquetées pour affecter chaque cluster à l’étiquette correspondante dans le cadre de l’apprentissage supervisé.

Invariance à l’augmentation de données

Au lieu de rapprocher les paires l’une de l’autre, on pousse les deux représentations à se trouver dans le même cluster.

Empêcher les solutions triviales

Dans une solution triviale, toutes les représentations sont identiques et appartiennent donc au même centroïde. Cependant, avec Sinkhorn, les différents clusters ont un nombre égal d’échantillons, de ce fait les représentations ne peuvent pas être placées dans un seul centroïde. Cela empêche ainsi une solution triviale.

« Autres méthodes »

La fonction de perte de toutes les méthodes précédentes, y compris les méthodes contrastives, nécessite un batch ou un pool d’échantillons négatifs, ce qui pose des problèmes pour l’entraînement distribué. Cependant, les fonctions de perte de ces méthodes sont locales. Ces méthodes sont performantes mais on ne comprend pas encore pourquoi elles ne s’effondrent pas. Il y a probablement une régularisation implicite dans ces réseaux qui les empêche de converger vers une solution triviale.

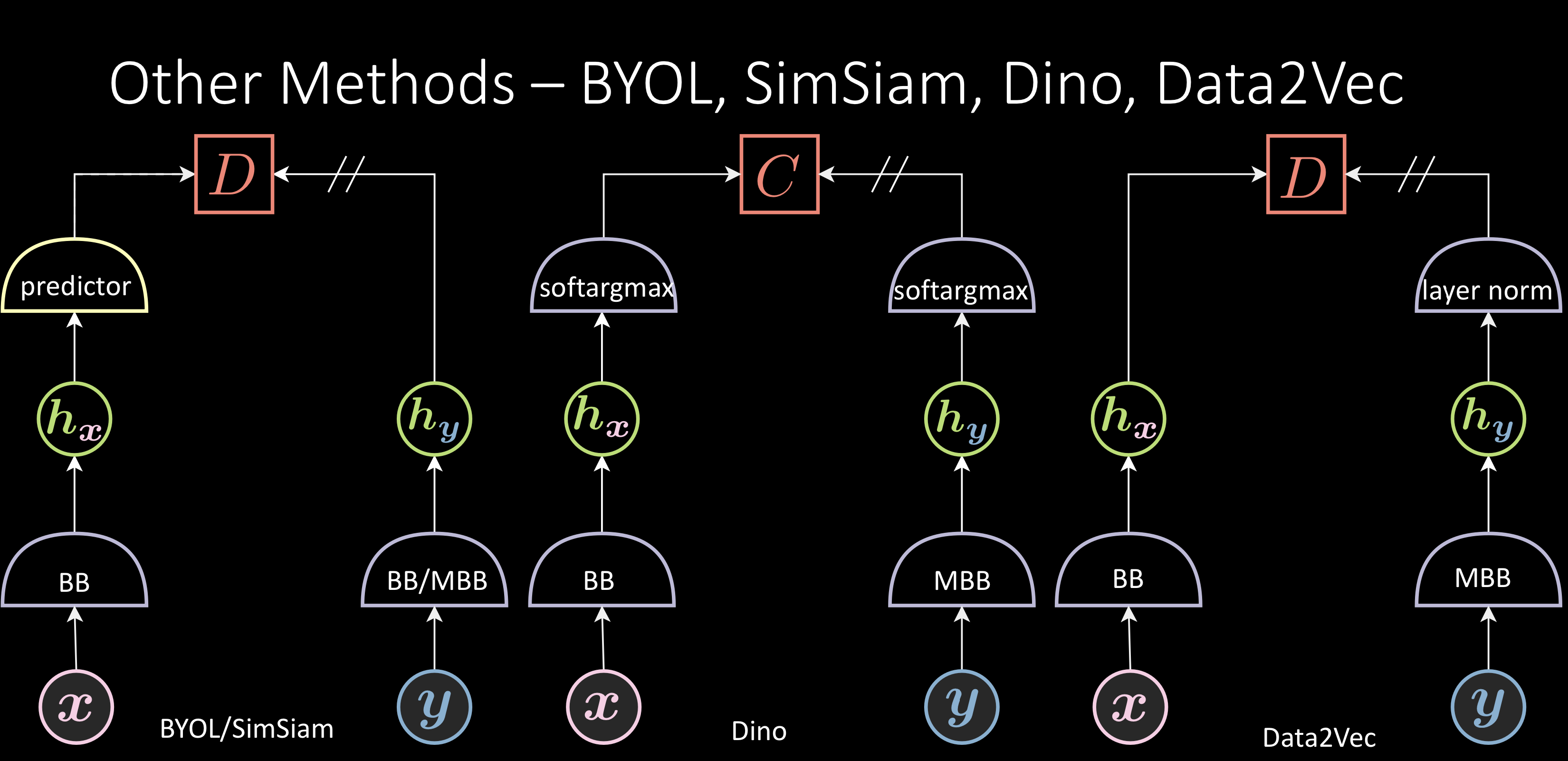
Figure 2 : Autres méthodes

BYOL

BOYL ajoute un prédicteur, prédisant $\green{h_{\vy}}$ à partir de $\green{h_{\vx}}$. La fonction d’énergie ( $\red{D}$ ) est une similarité cosinus entre $\green{h_{\vy}}$ et le $\green{h_{\vy}}$ prédit. Il n’y a pas de terme pour les échantillons négatifs, c’est-à-dire que cette méthode ne fait que rapprocher les paires positives et n’a aucune action sur les paires négatives. On pense que l’architecture asymétrique avec des couches supplémentaires permet à cette méthode de fonctionner.

SimSiam est une version postérieure qui utilise un backbone normal au lieu d’un backbone avec momentum.

Dino

Les deux composants softargmax utilisés ont une froideur/température différente. La fonction d’énergie est l’entropie croisée entre ces deux, rapprochant ces composants. Cette méthode n’impose rien sur les échantillons négatifs.

Data2Vec

Ajoute une couche de norme à la fin de la représentation.

Initialisation du réseau

Si vous initialisez le réseau avec une solution triviale, alors ce réseau ne fonctionnera jamais. En effet, si la solution triviale est déjà atteinte, la fonction de perte produira un gradient nul et ne pourra donc jamais s’échapper de la solution triviale. Cependant, dans d’autres cas, la dynamique d’entraînement est ajustée de telle sorte qu’ils ne convergent jamais dans ces méthodes.

Améliorations pour les JEMs

Nous pouvons encore améliorer ces modèles en faisant des expériences sur l’augmentation des données et l’architecture du réseau. Nous n’avons pas une bonne compréhension de ces éléments, mais ils sont très importants. En fait, trouver une bonne augmentation peut améliorer les performances plus que la modification de la fonction de perte.

Augmentation de données

La plupart des augmentations dominantes ont été proposées par SimCLR et améliorées un peu par BYOL :

1. Recadrage aléatoire (le plus critique)
2. Retournement
3. Variation de couleur
4. Flou gaussien

Il a été constaté empiriquement que le recadrage aléatoire est le plus critique. Cela pourrait être dû au fait que le recadrage aléatoire est le seul moyen de modifier l’information spatiale des images. Le retournement fait la même chose en partie, mais il est faible. La variation de couleur et le flou gaussien changent les canaux.

Figure 3 : Augmentation de données

Augmentation masquée

Récemment, les chercheurs se sont tournés vers l’augmentation par masquage au lieu de l’augmentation traditionnelle dans laquelle nous masquons la plupart (~75% dans l’image ci-dessous) des patchs. Elle peut remplacer le recadrage aléatoire car c’est une autre façon de supprimer la redondance de l’information spatiale.

Problèmes : Cela ne fonctionne bien qu’avec une architecture de type transformer et non avec de type ConvNet. En effet, le masquage introduit trop de bords artificiels aléatoires. Pour n’importe quel transformer, la première couche est la couche ConvNet, avec une taille de noyau égale à la taille du patch, ce qui fait qu’il n’y a jamais de bords artificiels. Pour les ConvNets qui ont des fenêtres glissantes, les bords artificiels ne peuvent pas être ignorés et se traduiront par du bruit.

Figure 4 : Augmentation par masquage

Projecteur/Expandeur

Il s’agit d’un réseau neuronal feed-forward à deux/trois couches et les résultats empiriques montrent qu’il est toujours préférable de l’ajouter dans l’architecture du réseau.

Le projecteur est utilisé pour projeter dans une dimension inférieure et l’extenseur est utilisé pour projeter dans une dimension supérieure. Le projecteur n’est utilisé que pendant le pré-entraînement et est supprimé pendant l’exécution de la tâche en aval. En effet, le projecteur supprime beaucoup d’informations même si la dimension de sortie du projecteur et du backbone est la même.

Encodeur avec momentum

Même sans banque mémoire, un encodeur avec momentum aide généralement à la performance des tâches en aval, surtout avec une faible augmentation de données.

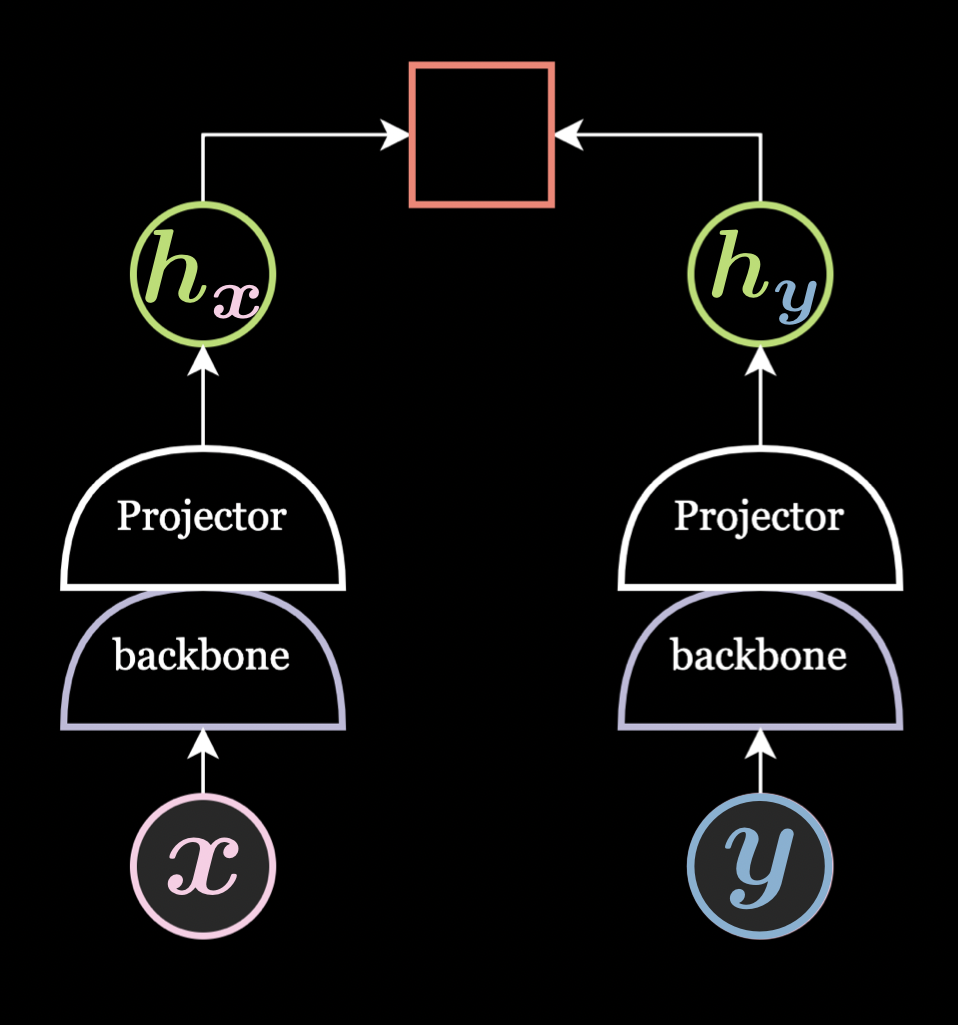
Figure 5 : Projecteur/Extenseur