Reconnaissance vocale et Graph Transformer Network II
🎙️ Awni HannunTemps d’inférence
L’inférence pour obtenir la transcription d’un signal audio donné peut être formulée en utilisant deux distributions :
- Le modèle acoustique (de l’audio à la transcription), représenté par $P(\mY \mid \mX)$.
- Le modèle linguistique, représenté par $P(\mY)$.
L’inférence finale est obtenue en prenant la somme des probabilités logarithmiques de ces deux modèles, c’est-à-dire :
\[\vect{\mY*} = \underset{\mY}{\operatorname{argmax}} \log P(\mY \mid \mX) + \log P(\mY)\]Nous utilisons le terme supplémentaire pour nous assurer que la transcription est conforme aux règles de la langue. Sinon, nous risquons d’obtenir une transcription grammaticalement incorrecte.
Recherche en faisceau
Lors de la génération d’une séquence, nous pouvons suivre l’approche gloutonne où nous prenons la valeur maximale de $P(\vy_{t} \mid \vy_{t-1}…\vy_{1})$.
Cependant, nous pouvons manquer une bonne séquence qui peut ne pas avoir la valeur maximale de $P(\vy_{t} \mid …)$ comme l’illustre l’exemple ci-dessous.
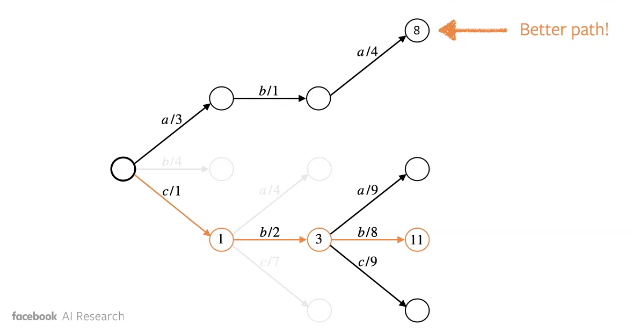
Figure 1 : Approche gloutonne (en bleue) : une solution moins optimale
Pour remédier à cela, nous employons la recherche en faisceau. Grossièrement, nous considérons les jetons maximum $k$ en termes de probabilité à chaque étape $t$ de la séquence. Pour chacun de ces n-grammes, nous poursuivons la recherche et trouvons le maximum.
L’illustration ci-dessous montre comment la recherche en faisceau peut conduire à une meilleure séquence.

Figure 2 : Recherche en faisceau : étape 1
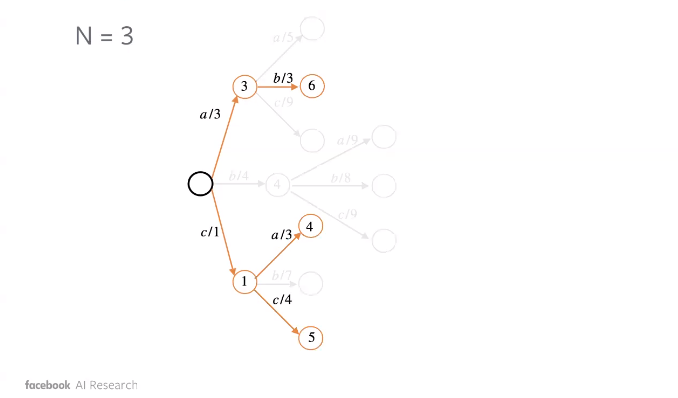
Figure 3 : Recherche en faisceau : étape 2
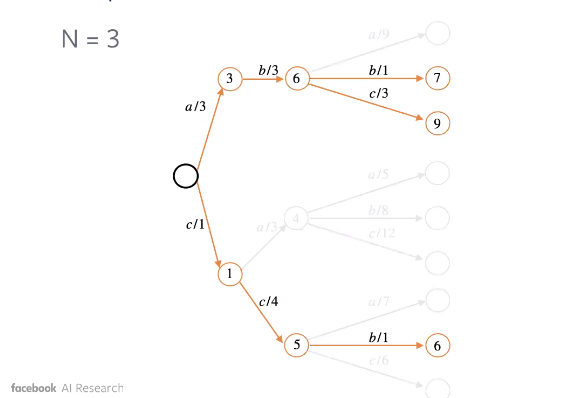
Figure 4 : Recherche en faisceau : étape 3
Graph Transformer Networks
Nous avons vu précédemment le Weighted Finite State Acceptor (WFSA) pour représenter les alginements dans un graphe.
Les Graph Transformer Networks (GTNs) sont essentiellement des WSFAs avec une différenciation automatique.
Examinons les principales différences entre les réseaux de neurones (NNs) et les GTNs.
| NN | GTN | |
|---|---|---|
| Structure de données de base | Tenseur | Graphe/WFSA |
| Multiplémentation matricielle | Compose | |
| Opérations de base | Opérations de réduction (Somme, Produit) | Distance la plus courte (Viterbi, Forward) |
| Négation, Addition, Soustraction, … | Fermeture, Union, Concaténation, … |
Pourquoi des WSFAs différentiables ?
- Encodage des a priori : facile d’encoder les a priori dans un graphe.
- Bout en bout : permet de faire le pont entre le processus d’entrâinement et de test
- Faciliter la recherche académique : lorsque nous séparons les données du code, il est plus facile d’explorer différentes idées. Dans notre cas, le graphe est la donnée et le code est l’opération, ce qui nous permet d’explorer différentes idées en modifiant le graphe.
Critères de séquence avec WFSAs
Il s’avère que de nombreux critères de séquence peuvent être spécifiés comme la différence entre deux scores forward.
- Graphes A : fonction de l’entrée $\mX$ (parole) et de la sortie cible $\mY$ (transcription).
- Graphe Z : fonction de l’entrée $\mX$, qui sert de normalisation.
- Perte : $\log P(\mY \mid \mX) = \text{forwardScore}(A_{\mX,\mY}) - \text{forwardScore}(Z_{\mX})$.
Des fonctions de perte courantes en reconnaissance automatique de la parole :
- Critère de segmentation automatique (ASG pour Automatic Segmentations Criterion)
- Classification Temporale Connectioniste (CTC pour Connectionist Temporal Classification)
- MMI sans treillis (LF-MMI pour Lattice Free Maximum Mutual Information)
Nombre de lignes de code pour implémenter la CTC
| Lignes | |
|---|---|
| Warp-CTC | 9,742 |
| wav2letter | 2,859 |
| PyTorch | 1,161 |
| gtn | 30* |
*Le même code fonctionne pour le décodage.
Différents types d’états finis pondérés
Accepteur d’états finis pondérés (WFSA pour Weighted Finite-State Acceptor)
Le cercle en gras est l’état de départ et l’état d’acceptation est celui avec les cercles concentriques.
Exemple
Un WFSA simple reconnaît les séquences aa et ab avec comme score :
- Le score de aa est $0 + 2 = 2$
- Le score de ba est $1 + 2 = 3$
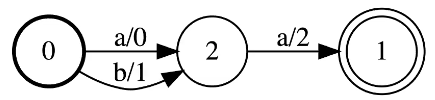
Figure 5 : Accepteur d'états finis pondérés (WFSA) à trois nœuds
Transducteur à états finis pondérés (WFST pour Weighted Finite-State Transducer)
Ces graphes sont appelés transducteurs car ils transforment des séquences d’entrée en séquences de sortie.
Exemple
Un WFST simple reconnaît ab à xz et bb à yz avec comme score :
- Le score de ab $\to$ xz est $1,1 + 3,3 = 4,4$
- Le score de bb $\to$ yz est de $2,0 + 3,3 = 5,3$

Figure 6 : Transducteur d'états finis pondérés (WFST) à trois nœuds
Plus de WFSAs et WFSTs
- Les cycles et les boucles sont autorisés.
- Les nœuds de départ et d’arrivée multiples sont autorisés.
- Les transitions de type $\epsilon$ (c’est-à-dire faisant rien) sont autorisées dans les WFSAs et WFSTs.
Les différentes opérations
Union
L’union accepte une séquence si elle est acceptée par l’un des graphes d’entrée.

Figure 7 : Opération d'union entre trois graphes
Etoile de Kleene
Accepte toute séquence acceptée par le graphe d’entrée répétée 0 fois ou plus.
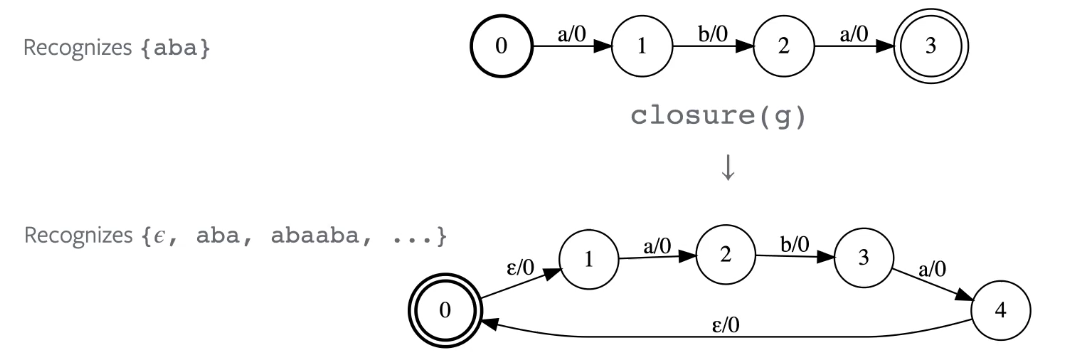
Figure 8 : Opération de l'étoile de Kleene
Intersection
Similaire à la multiplication matricielle ou à la convolution. Cette opération est probablement la plus importante dans les GTNs.
- Tout chemin qui est accepté par les deux WFSA est accepté par le produit de l’intersection.
- Le score du chemin instersecté est la somme des scores des chemins des graphes d’entrée.
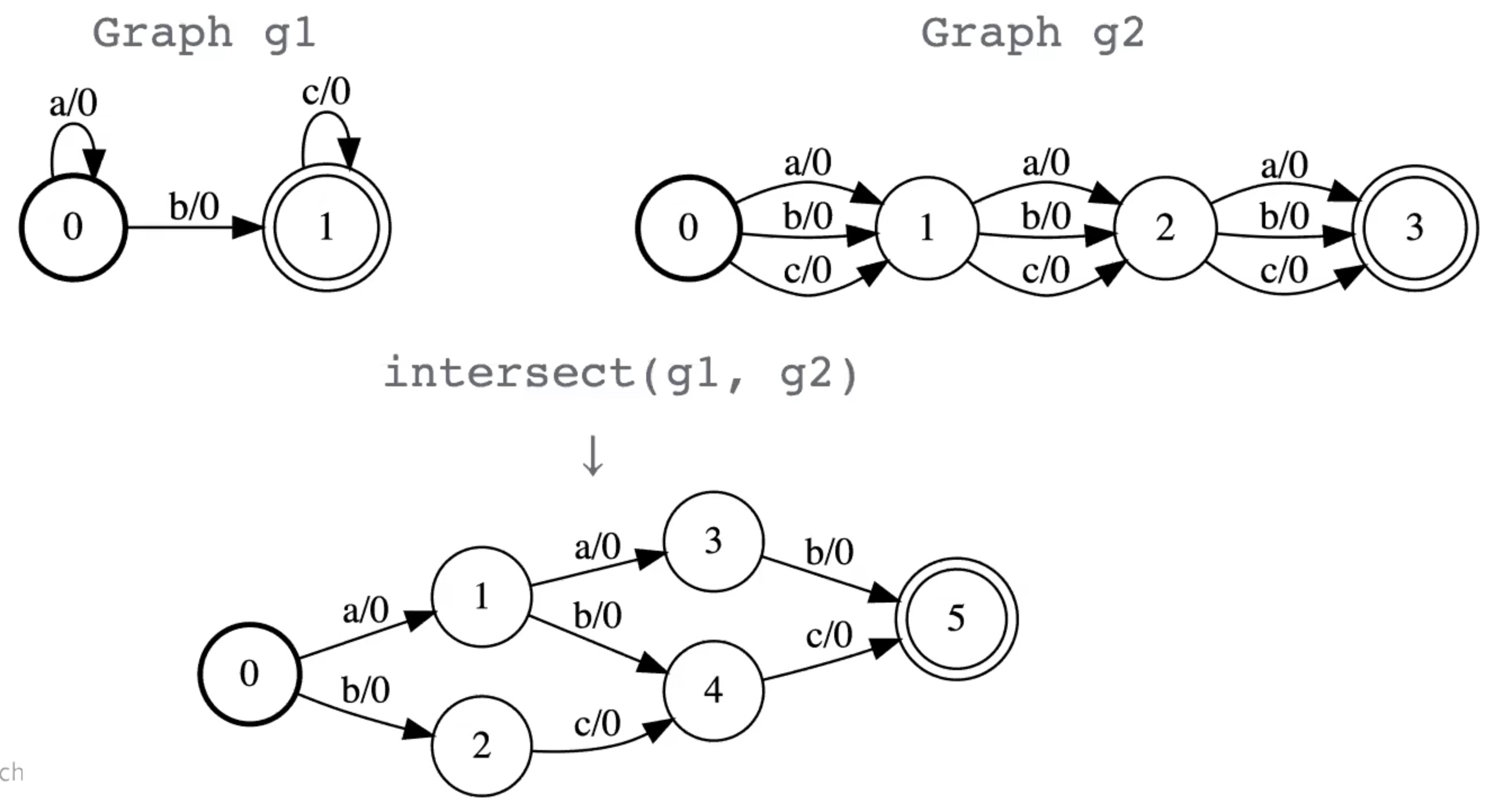
Figure 9 : Opération d'intersection entre deux graphes
Composition
C’est essentiellement la même chose que l’intersection mais pour les transducteurs au lieu des accepteurs.
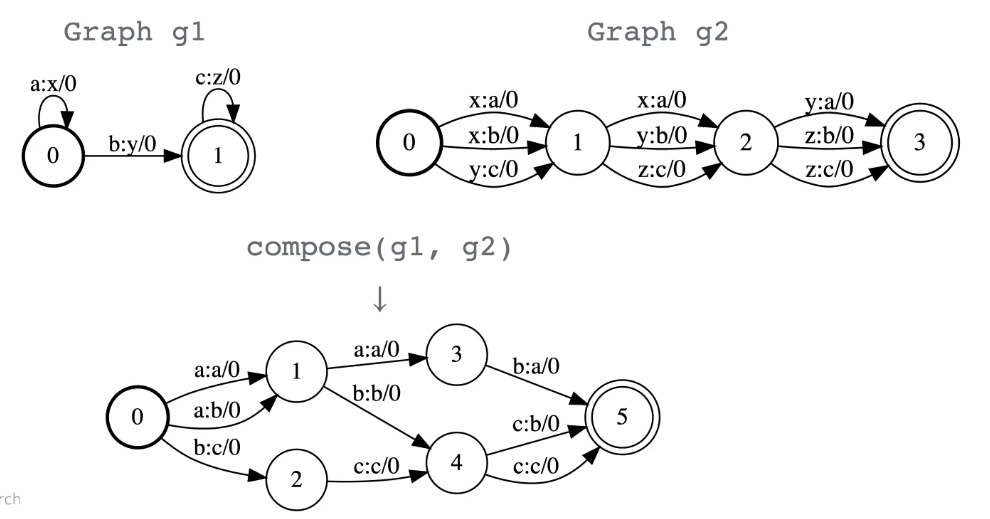
Figure 10 : Opération de composition entre deux graphes
La principale chose à propos de la composition est qu’elle permet de faire des correspondances à partir de différents domaines. Par exemple, si nous avons un graphe qui fait correspondre des lettres aux mots et un autre graphe qui fait correspondre des mots aux phrases, alors lorsque nous composons ces deux graphes nous faisons correspondre des lettres aux phrases.
Score forward
Supposons que le graphe est DAG (c’est-à-dire dirigé et sans boucles) et avons un algorithme de programmation dynamique efficace.
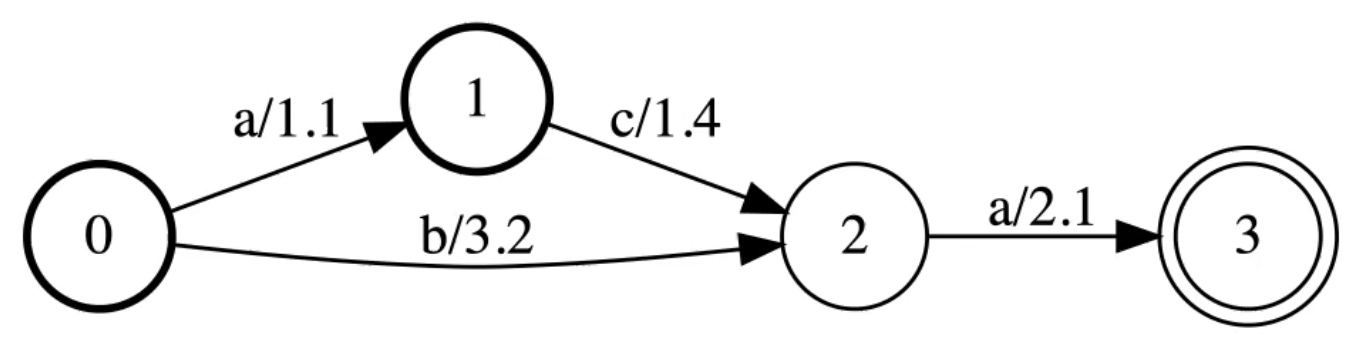
Figure 11 : Le score forward est la SoftMax des chemins
Les graphes acceptent trois chemins :
- aca avec comme score $1,1 + 1,4 + 2,1$
- ba avec comme score $3,2 + 2,1$
- ca avec commescore $1,4 + 2,1$
Le ForwardScore(g) est la SoftMax réelle des chemins.
Séquence de critères avec WFSTs
Graphe cible $\mY$
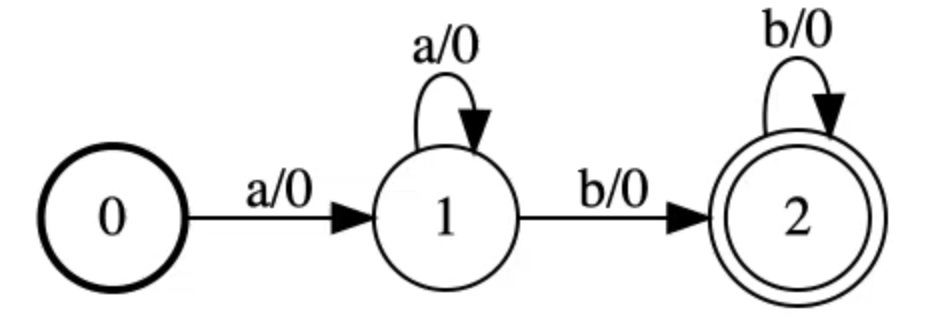
Figure 12 : Graphe cible Y
Graphe des émissions E
Entre deux nœuds nous avons des logits.

Figure 13 : Graphe des émissions E
Graphe contraint par la cible A par intersection ($\mY$, E)
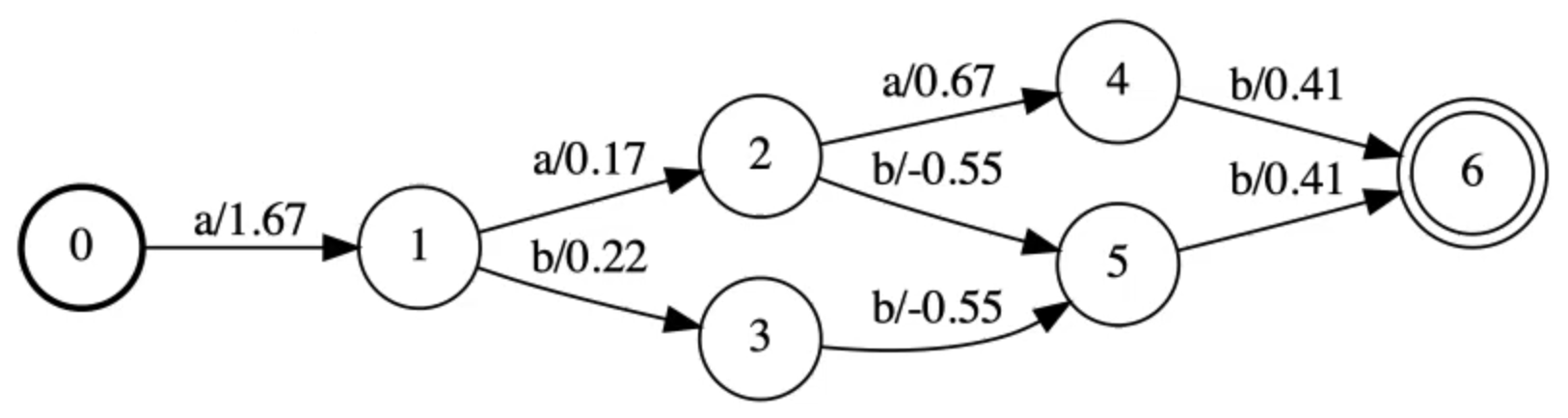
Figure 14 : Graphe contraint par la cible
Perte
\[\ell = - (\text{forwardScore}(A) - \text{forwardScore}(E))\]Ce n’est pas la CTC mais ça s’en approche.
Exemples de code
Créer le graphe cible
Similaire à la figure 8.
import gtn
# On crée le graphe
target = gtn.Graph(calc_grad=False)
# Ajouts des noeuds
target.add_node(start=True)
target.add_node()
target.add_node(accept=True)
# Ajouts des arcs
target.add_arc(src_node=0, dst_node=1, label=0)
target.add_arc(src_node=1, dst_node=1, label=0)
target.add_arc(src_node=1, dst_node=2, label=1)
target.add_arc(src_node=2, dst_node=2, label=1)
# On dessine le graphe
label_map = {0: 'a', 1: 'b'}
gtn.draw(target, "target.pdf", label_map)
Faire le graphe des émissions
Similaire à la figure 9.
import gtn
# Tableau des émissions (logits)
emissions_array = np.random.randn(4, 3)
# Créer le graphe
emissions = gtn.linear_graph(4, 3, calc_grad=True)
# Définir les poids
emissions.set_weights()
L’ASG dans GTN
Étapes
- Calculer les graphes
- Calculer la perte
- Gradients automatiques
from gtn import *
def ASG(emissions, target):
# Etape 1
# Calculs des graphes :
A = intersect(target, emissions)
Z = emissions
# Etape 2
# Forward both.graphs :
A_score = forward(A)
Z_score = forward(Z)
# Compute loss:
loss = negate(subtract(A_score, Z_score))
# Etape 3
# Nettoyage des gradients précédents
emissions.zero_grad()
# Calcul des gradients
backward(loss, retain_graph=False)
return loss.item(), emissions.grad()
CTC dans GTN
from gtn import *
def CTC(émissions, "target") :
# Etape 1
# Calculs des graphes :
A = intersect(target, emissions)
Z = emissions
# Etape 2
# Forward both.graphs :
A_score = forward(A)
Z_score = forward(Z)
# Compute loss:
loss = negate(subtract(A_score, Z_score))
# Etape 3
# Nettoyage des gradients précédents
emissions.zero_grad()
# Calcul des gradients
backward(loss, retain_graph=False)
return loss.item(), emissions.grad()
La seule différence est la cible ici. Elle rend très facile l’essai de différents algorithmes et gtn est censé être similaire à PyTorch avec une structure de données et des opérations différentes.
Lectures supplémentaires
- Sur la CTC :
- Sur le GTN :
- Sur les GTNs modernes :
📝 Gyanesh Gupta, Abed Qaddoumi
Loïck Bourdois
14th April 2021