Apprentissage autosupervisé en vision par ordinateur

La vision par ordinateur se concentre actuellement sur l’apprentissage de représentations visuelles à partir de données supervisées et sur l’utilisation de ces représentations/poids comme initialisations pour d’autres tâches qui ne disposent pas de données étiquetées. Cet étiquetage des données peut s’avérer coûteux. Par exemple, le jeu de données ImageNet compte environ $14$ millions d’images et $22 000$ catégories et son étiquetage a nécessité environ $22$ années de travail.

Tâche de prétexte

La tâche de prétexte est une tâche d’apprentissage autosupervisée effectuée dans le but d’apprendre des représentations visuelles afin de les utiliser pour d’autres tâches en aval (c’est-à-dire la classification, la détection d’objets, etc.). La tâche de prétexte est généralement effectuée sur une propriété inhérente au jeu de données lui-même.

Tâches de prétextes populaires pour les images :

1. Prédire la position relative des patchs dans une image.
2. Prédire le type de permutation des patchs de l’image (puzzles).
3. Prédire le type de rotation appliquée

Qu’est-ce qui manque aux tâches de prétextes ?

Il y a un décalage assez important entre ce qui est résolu avec les tâches de prétextes et ce qui doit être réalisé par les tâches de transfert. Ainsi, le pré-entraînement n’est pas adaptée aux tâches finales. Les performances de chaque couche peuvent être évaluées (à l’aide de classifieurs linéaires) afin de déterminer les caractéristiques de la couche à utiliser pour les tâches de transfert.

Les caractéristiques pré-entraînées doivent satisfaire deux propriétés fondamentales :

1. elles doivent représenter la façon dont les images sont liées les unes aux autres
2. être robuste aux facteurs de nuisance

Méthode populaire pour l’apprentissage autosupervisé

Une méthode populaire et commune en apprentissage autosupervisé consiste à apprendre des caractéristiques qui sont robustes à l’augmentation de données. C’est à dire apprendre des caractéristiques telles que :

Les caractéristiques produites par le réseau pour une image doivent être stables sous différents types de techniques d’augmentation de données. Cette propriété est extrêmement utile car les caractéristiques vont être invariantes aux facteurs de nuisance.

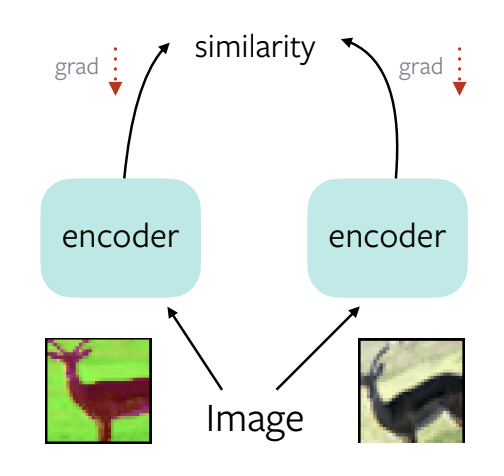
Figure 1 : Une solution triviale pour l'apprentissage de représentations autosupervisées

Prenez une image, appliquez-lui deux augmentations de données différentes, faites-la passer par un encodeur, calculez la similarité. Puis faites une rétropropagation avec les gradients obtenus. Le réseau apprend alors à produire une représentation constante pour les deux augmentations.

Le problème est qu’il existe une solution triviale consistant à produire les mêmes caractéristiques pour toutes les images d’entrée. Les représentations s’effondrent alors et deviennent inutilisables pour les tâches de reconnaissance en aval.
Toutes les architectures autosupervisées abordées dans la suite essaient donc d’obtenir des performances semblables à l’approche supervisée tout en évitant les solutions triviales. Il est d’ailleurs possible de les classer par famille en fonction de la manière dont chacune d’elles traite ce problème de solutions triviales.

Catégorisation des méthodes autosupervisées récentes :

1. Objectif de maximisation de la similarité
2. Objectif de réduction de la redondance

Pour l’évaluation, un sous-ensemble d’ImageNet $(1,3$ million d’images dans $1000$ catégories) non étiqueté est utilisé pour pré-entraîner un modèle Resnet-50 initialisé de manière aléatoire.

Quelles sont les différentes façons de réaliser l’apprentissage par transfert et d’évaluer ses performances?

Nous pouvons faire l’une des deux choses suivantes :

1. Un classifieur linéaire sur les caractéristiques fixes produites par le réseau (pour les tâches de classification).
2. Finetuner l’ensemble du réseau pré-entraîné sur la tâche cible (pour les tâches de détection).

Apprentissage contrastif

Fonction de perte : les enchâssements d’images liées doivent être plus proches que les enchâssements d’images non liées.

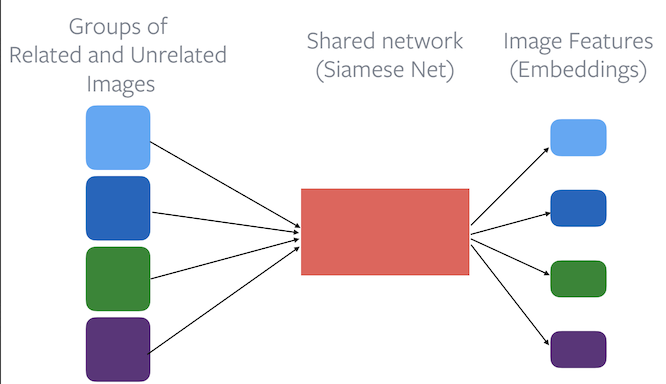
Figure 2 : l'utilisation d'un encodeur de base dans l'apprentissage contrastif

Les différentes méthodes d’apprentissage contrastif comprennent :

1. PIRL (Pretext-Invariant Representation Learning)
2. SimCLR (Simple Framework for Contrastive Learning of Visual Representations)
3. MoCo (Momentum Contrast)

PIRL

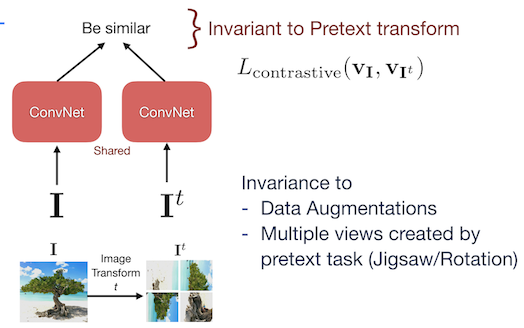
Figure 3 : Architecture de PIRL

Une image $I$ et son augmentation $I^t$ sont passées à travers le réseau et la perte d’apprentissage contrastive est appliquée de manière à ce que le réseau devienne invariant à la tâche de prétexte. L’objectif est d’obtenir une similarité élevée pour les caractéristiques de l’image et du patch appartenant à la même image ainsi qu’une faible similarité pour les caractéristiques provenant d’autres images aléatoires. La tâche prétexte de PIRL essaie d’obtenir une invariance sur les augmentations de données plutôt que de prédire l’augmentation des données.

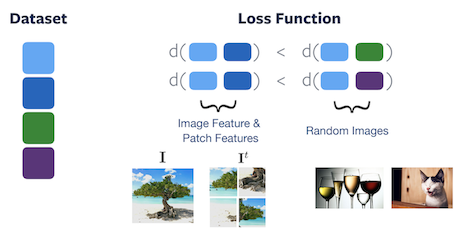
Figure 4 : Fonction de perte de PIRL

Caractéristiques sémantiques

Figure 5 : Performance du pré-entraînement en utilisant PIRL vs Jigsaw à chaque couche

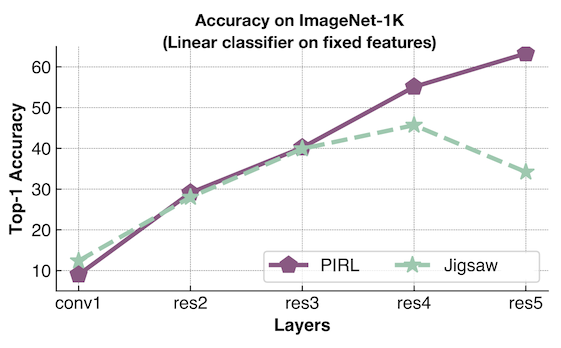
• Un classifieur linéaire est utilisé à chaque couche pour sonder et calculer la précision. L’un est entraîné en utilisant PIRL et l’autre en utilisant Jigsaw (tâche consistant à résoudre un puzzle).
• Jigsaw essaie de prédire la permutation, tandis que PIRL essaie d’y être invariant.
• Les performances de PIRL ne cessent d’augmenter, ce qui indique que la fonction est de plus en plus alignée sur les tâches de classification en aval.
• Jigsaw essaie de retenir les informations de la tâche de prétexte, les performances plafonnent puis chutent brusquement. Il finit par ne pas être performant pour les tâches de transfert.

Échantillonnage des positifs et des négatifs

Il existe plusieurs façons d’obtenir des échantillons qui constituent des paires apparentées (positives) et non apparentées (négatives) :

1. Patchs d’une image : les modèles basés sur le codage prédictif contrastif (CPC, Contrastive Predictive Coding en anglais) utilisent les zones d’une image qui sont proches les unes des autres comme positives (liées) et les zones qui sont éloignées les unes des autres comme négatives (non liées).

2. Patchs d’images : les patchs d’une même image sont considérés comme apparentés et les patchs de 2 images différentes sont considérés comme non apparentés. Utilisé dans MoCo et SimCLR

3. Vidéos : les images qui sont proches dans l’espace temporel sont liées et celles qui sont éloignées ne sont pas liées.

4. Multimodal - Vidéo et audio : les séquences vidéo et les séquences audio correspondantes sont liées. Les séquences vidéo d’une vidéo et les séquences audio d’une autre vidéo ne sont pas liées.

5. Pistage (tracking) d’objets vidéo : un objet est suivi à travers plusieurs images d’une vidéo. Les zones de détection d’une même vidéo sont liées. Les patchs de détection de différentes vidéos ne sont pas liés.
   

Quelle est la propriété fondamentale de l’apprentissage contrastif qui empêche les solutions triviales ?

Figure 6 : Fonction de perte de l'apprentissage contrastif

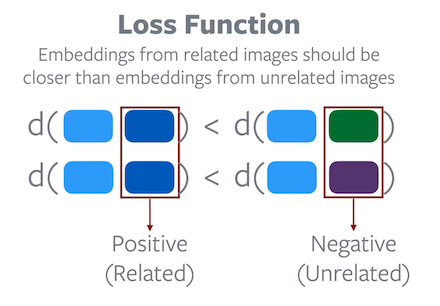
La fonction objectif de l’apprentissage contrastif est conçue pour éviter les solutions triviales. L’objectif de la fonction est de s’assurer que la distance entre les paires d’enchâssements positives est inférieure à la distance entre les paires d’enchâssements négatives. Par conséquent, une solution triviale où une distance constante est attribuée à toutes les paires d’enchâssements est impossible à atteindre par un processus de minimisation de la fonction objective donnée. Cependant, les recherches ont montré que de bonnes paires négatives sont cruciales pour que l’apprentissage contrastif fonctionne bien.

SimCLR

Dans SimCLR, deux vues corrélées d’une image sont créées en utilisant des augmentations telles que des patchs aléatoire, le redimensionnement, les distorsions de couleur et le flou gaussien. Un encodeur de base est utilisé avec une tête de projection pour obtenir des représentations qui sont utilisées pour effectuer un apprentissage contrastif.

Il utilise une grande taille de batch pour générer des échantillons négatifs. Le batch peut être réparti sur plusieurs GPUs de manière indépendante. Les images d’un GPU peuvent être considérées comme négatives pour celles d’un autre GPU.

Avantages de SimCLR :

1. Simple à implémenter

Désavantages de SimCLR :

1. Une grande taille de batch est requise
2. Un grand nombre de GPU est requis

Comment résoudre le problème de calcul dans SimcLR ?

Une banque mémoire peut être utilisée pour maintenir un momentum d’activations sur toutes les caractéristiques. À chaque passage en avant d’une image, les caractéristiques de la banque mémoire sont mises à jour en utilisant les nouveaux enchâssements. Les caractéristiques de la banque mémoire peuvent ensuite être utilisées comme négatives pour la perte contrastive.

Avantages de la banque mémoire :

• Efficace en termes de calcul. Nécessite une seule passe en avant pour calculer les enchâssements.

Inconvénients de la banque mémoire :

• Pas en ligne. Les fonctionnalités deviennent très vite obsolètes.
• Nécessite une grande quantité de mémoire vive du GPU.
• Difficile de faire évoluer le stockage vers des millions d’images.

MoCo

MoCo est une méthode contrastive qui utilise une banque mémoire pour maintenir un momentum d’activations. Elle fonctionne en utilisant 2 encodeurs. L’encodeur $f_{\vtheta}$ est l’encodeur qui doit être appris. L’encodeur $f_{\vtheta_{\text{EMA}}}$ maintient une moyenne mobile exponentielle de $f_{\vtheta}$.

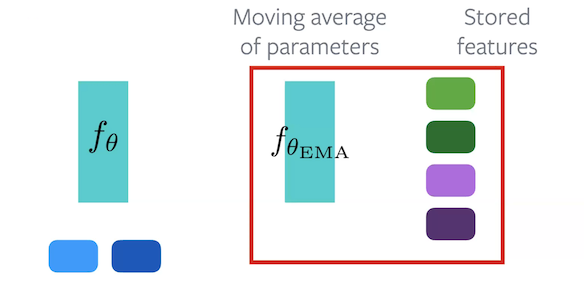
Figure 7 : Architecture de MoCo

Pendant la passe avant, chaque échantillon est passé à travers les deux encodeurs. Certains des enchâssements de $f_{\vtheta_{\text{EMA}}}$ sont gardés de côté pour être utilisés comme enchâssements négatifs. Pour l’algorithme, les enchâssements originales proviennent de $f_{\vtheta}$, les enchâssements positives de $f_{\vtheta_{\text{EMA}}}$ et les enchâssements négatives proviennent de l’ensemble des enchâssements stockées.

Avantages de MoCo :

• Peut être facilement adapté en termes d’utilisation de la mémoire car il n’est pas nécessaire de stocker l’ensemble des données.
• C’est une solution en ligne, car la moyenne mobile est continuellement mise à jour.

Inconvénients de MoCo :

• Deux passes avant nécessaires, une par $f_{\vtheta}$ et une autre par $f_{\vtheta_{\text{EMA}}}$.
• Mémoire supplémentaire requise pour les paramètres/caractéristiques stockés.

Méthodes de clustering

Comment l’apprentissage contrastif et le clustering sont liés l’un à l’autre ?

Dans l’apprentissage constrastif, chaque échantillon comporte des éléments positifs et négatifs correspondants. Le but de la tâche d’apprentissage est d’essayer de rassembler les enchâssemnts positifs tout en repoussant les enchâssemnts négatifs. Nous créons donc essentiellement des groupes dans l’espace des caractéristiques.

Le clustering est un moyen plus direct de réaliser le regroupement car il crée naturellement des groupes dans l’espace des caractéristiques.

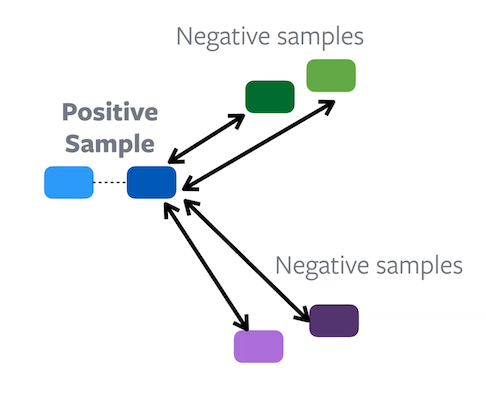
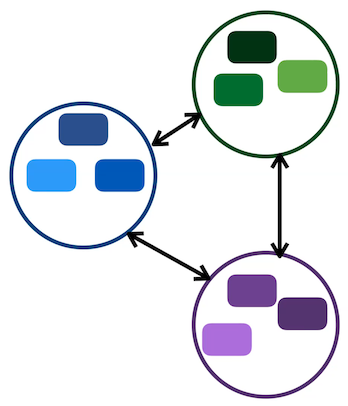
Figure 8 : Différence entre l'apprentissage contrastif (à gauche) et le clustering (à droite)

SwAV

L’algorithme SwAV (Swapping Assignments between Views) est une méthode de clustering en ligne. L’idée ici est de maximiser la similarité d’une image donnée $I$ et de l’augmentation de cette image $\text{augment}(I)$ et, ce faisant, de s’assurer qu’elles appartiennent au même cluster.

Les échantillons et leurs augmentations sont représentés par différentes nuances de la même couleur. La similarité de l’enchâssement de chaque échantillon avec chacun des prototypes (centres des clusters) est calculée. L’échantillon est alors assigné au prototype ayant la plus grande similarité. L’objectif du réseau est d’affecter une image et son augmentation au même prototype.

Peut-il conduire à une solution triviale ?

Une solution triviale est possible lorsque chaque échantillon est affecté au même groupe/cluster/prototype. Cela entraîne une représentation effondrée pour toute entrée donnée.

Comment éviter la solution triviale ?

1. Contrainte d’équipartition

   
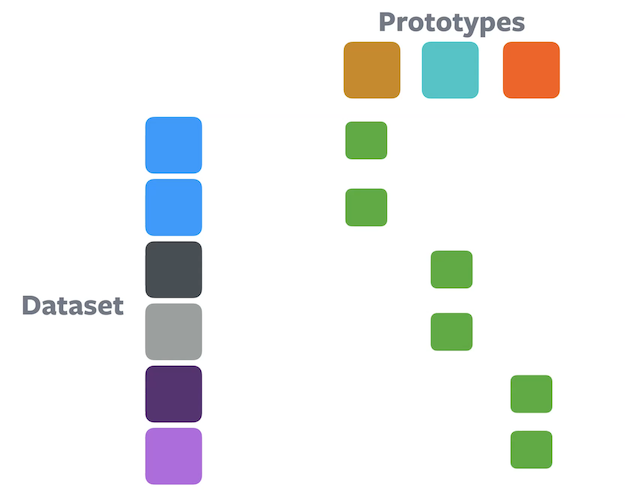
   Figure 9 : Clustering à l'aide d'une contrainte d'équipartition

   Étant donné $n$ échantillons et $k$ partitions, chaque cluster est autorisé à avoir un maximum de $n/k$ échantillons. Les enchâssements sont partitionnés de manière égale ce qui empêche la solution triviale du cluster unique. Les méthodes de clustering basées sur le transport optimal, comme l’algorithme de Sinkhorn-Knopp, garantissent intrinsèquement la contrainte.

2. Affectation douce

   
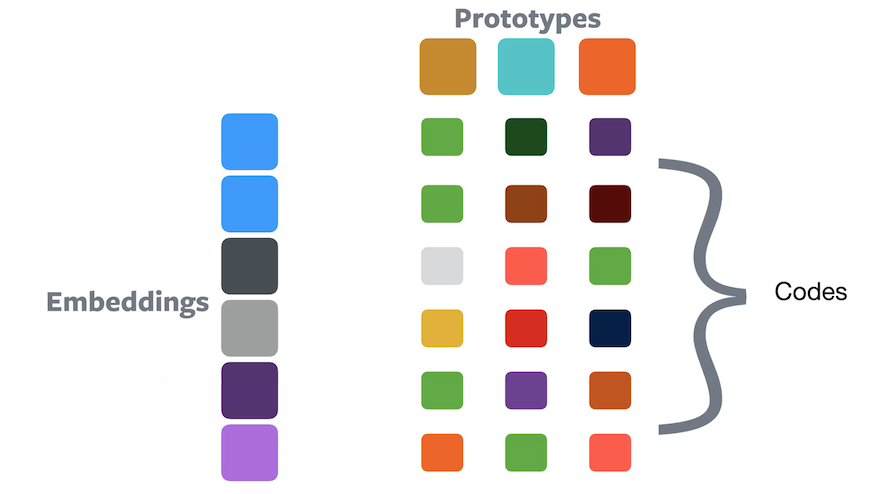
   Figure 10 : Clustering à l'aide de l'affectation douce

   Dans l’affectation douce, un échantillon appartient à tous les prototypes avec une certaine proportion de chacun d’entre eux, de sorte que leur somme soit égale à $1$. Les valeurs de composition peuvent être traitées comme un code qui indique comment chaque enchâssement est codé dans l’espace prototype.

Considérons le cas où nous avons un déséquilibre de classe élevé. Si nous utilisons la méthode d’équipartition, cela ne donnera-t-il pas des résultats inexacts ?

L’affectation douce résout ce problème en représentant beaucoup plus de classes que l’affectation dure. Elle donne une représentation plus riche et est moins sensible à $k$ (nombre de classes) et donc à $k/n$. Cependant, si l’affectation dure est utilisée, le déséquilibre des classes et la valeur fixe de $n/k$ créeront des imprécisions.

Entraînement de SwAV :

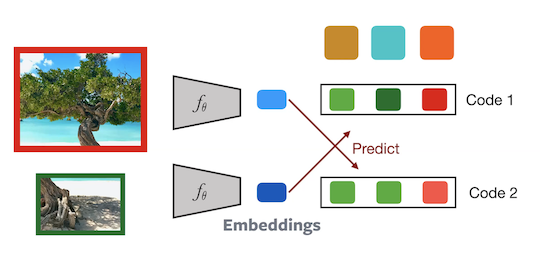
Figure 11 : Architecture de SwAV

Deux patchs d’une image sont passés par le réseau pour calculer les codes correspondants. Le code $2$ est alors prédit à partir de l’enchâsement $1$ et vice versa. Cette tâche force le réseau à devenir invariant aux augmentations de données. Les gradients sont également rétropropagés sur les prototypes. Ce modèle est donc mis à jour en ligne.

Avantages de SwAV :

1. Pas besoin de négations explicites
2. Les méthodes de transport optimales évitent les solutions triviales
3. Convergence plus rapide que l’apprentissage contrastif
   • L’espace des codes impose plus de contraintes et les enchâsements ne sont pas directement comparés
4. Moins d’exigences en matière de calcul
5. Un plus petit nombre (4-8) de GPUs est nécessaire

Pré-entraînement sur ImageNet sans étiquettes :

Même si ImageNet sans étiquettes peut être utilisé pour l’apprentissage autosupervisé, il existe un biais inhérent dans le jeu de données en raison du processus de sélection impliqué.

1. Les images appartiennent à $1000$ classes spécifiques
2. Les images contiennent un objet proéminent
3. Les images ont un encombrement très limité et très peu de concepts de fond

Pré-entraînement sur des données non-ImageNet

Le pré-entraînement sur des données non-ImageNet nuit aux performances.

Figure 12 : Exemple d'une image problématique provenant d'un jeu de données n'étant pas Imagenet

Considérons l’image ci-dessus. Un patch présente un réfrigérateur et l’autre pourrait être celui d’une table/chaise. L’algorithme essaie de créer des enchâssements similaires pour les deux car ils appartiennent à la même image. Ce n’est pas ce que nous attendons du processus d’entraînement.

Les données du monde réel ont des distributions très différentes. Il peut même s’agir d’images de dessins animés ou de memes et rien ne garantit qu’une image contiendra un seul (ou parfois, n’importe quel) objet proéminent.