Modèles génératifs

Auto-encodeurs (AE)

Les auto-encodeurs sont des réseaux neuronaux artificiels entraînés de manière non supervisée qui visent à apprendre la représentation des données d’entrée, puis à générer les données à partir des représentations codées apprises. Les auto-encodeurs peuvent être considérés comme un cas particulier d’inférence amortie où, au lieu de trouver la latente optimale pour produire une reconstruction appropriée de l’entrée, nous alimentons simplement la sortie de l’encodeur au décodeur.

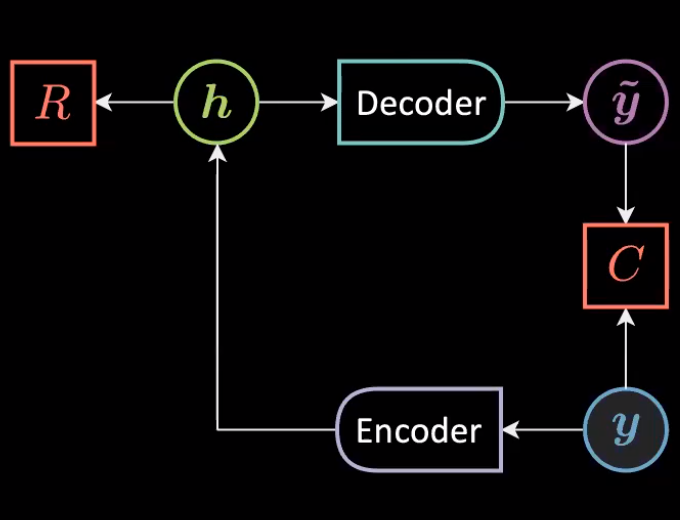
Figure 1 : Architeture générale d'un auto-encodeur

Nous pouvons exprimer mathématiquement l’architecture ci-dessus comme suit :

Avec les problèmes de dimensions suivants :

Les données sont représentées uniquement par $\vy$ car le but est de reconstruire les données qui vivent sur la variété (instance d’EBM inconditionnelle) par la fonction d’énergie suivante :

Auto-encodeur sous/sur complet

Dans un auto-encodeur, lorsque la dimension de la représentation cachée, $d$, ($30$) est inférieure à celle de la taille de l’entrée, $n$ ($784$), on peut parler d’auto-encodeur sous-complet.

Corrélativement, lorsque la dimension de la représentation cachée, $d$ est supérieure aux dimensions d’entrée, $n$, on dit qu’il s’agit d’un auto-encodeur sur-complet.

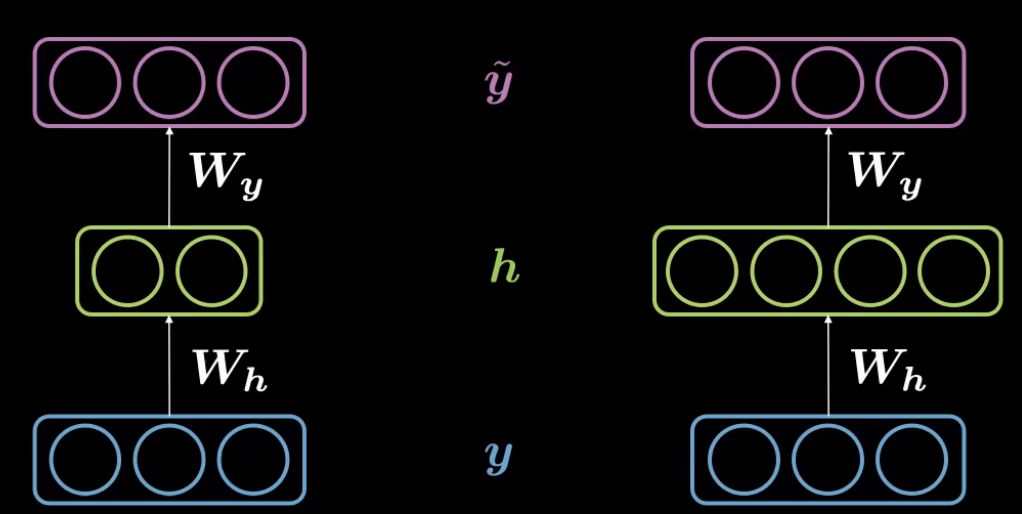
Figure 2 : Auto-encodeur sous-complet (à gauche) et sur-complet (à droite)

Nous travaillons avec des images MNIST $28 \times 28$ de telle sorte que la routine de transfomation est définie de $784 (=28 \times 28) \rightarrow 30$ sous l’encodeur suivi du décodeur qui fait correspondre $30 \rightarrow 784$. Les images sont normalisées et les valeurs des pixels $\in [-1,1]$.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(28 * 28, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, 28 * 28), # Rotation
            nn.Tanh(), # Squashing
        )

    def forward(self, y):
        h = self.encoder(y) # 784 -> 30
        y_tilde = self.decoder(h) # 30 -> 784
        return y_tilde

model = Autoencoder()
criterion = nn.MSELoss()

Figure 3 : Sortie générée par l'auto-encodeur sous-complet

Jetons un coup d’œil sur certains des noyaux de l’encodeur.

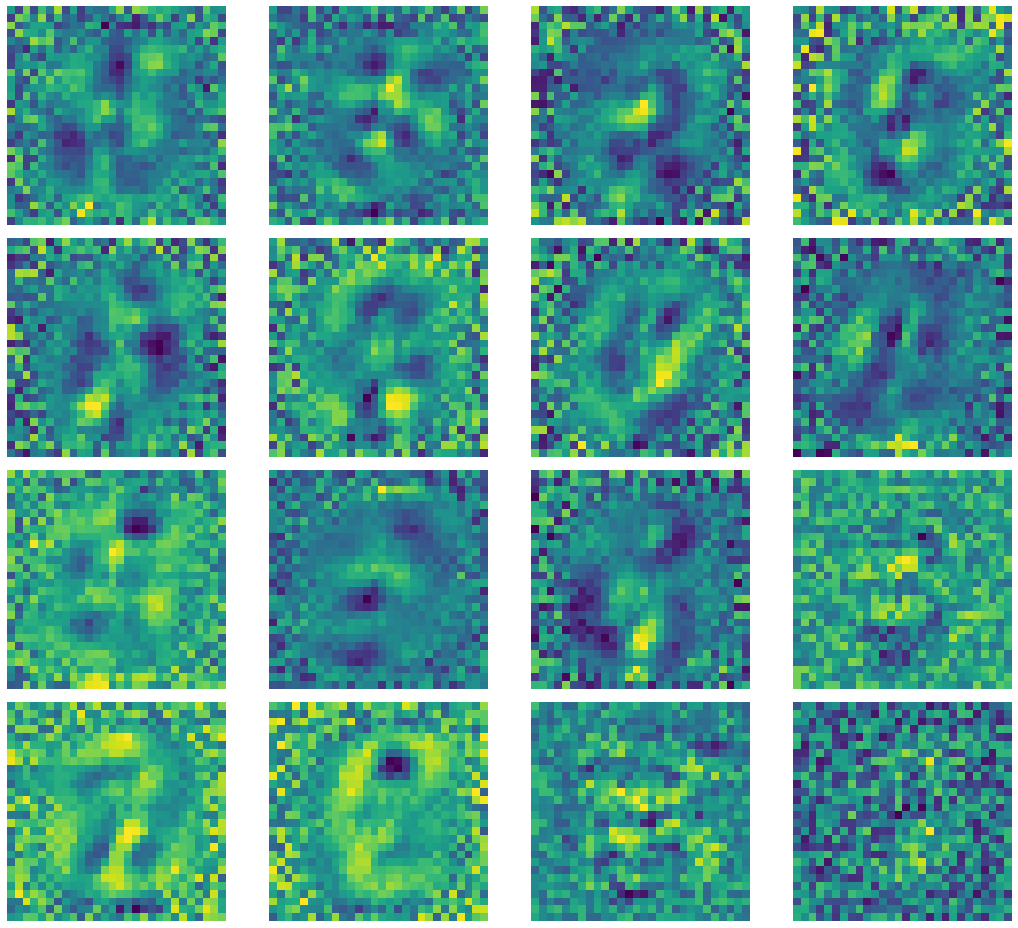
Figure 4 : Sorties du noyau de l'auto-encodeur sous-complet

Si vous remarquez qu’il apparaît un bruit de sel et de poivre entourant le centre des images, cela est dû à la faible fréquence spatiale le long de la région dans l’image d’entrée. Les $+1$ et $-1$ du bruit s’annulent à $0$, ce qui fait que leur contribution moyenne est de $0$. Des régions à haute fréquence apparaissent autour de la région centrale, car les chiffres des images MNIST sont centrés. Les noyaux avec seulement du bruit indiquent que le noyau correspondant s’est effondré ou est mort.

Auto-encodeur débruiteur (DAE)

Dans l’auto-encodeur débruiteur, nous prenons un échantillon d’un ensemble de données, nous injectons un certain bruit de sorte que l’auto-encodeur est obligé de reproduire l’échantillon original. Par conséquent, l’objectif est d’apprendre le champ vectoriel qui doit transformer l’échantillon corrompu en une partie débruitée. Ici, nous avons fixé $d=500$, ce qui est supérieur au nombre de pixels réellement utilisés pour représenter les chiffres dans les images (AE sur-complet).

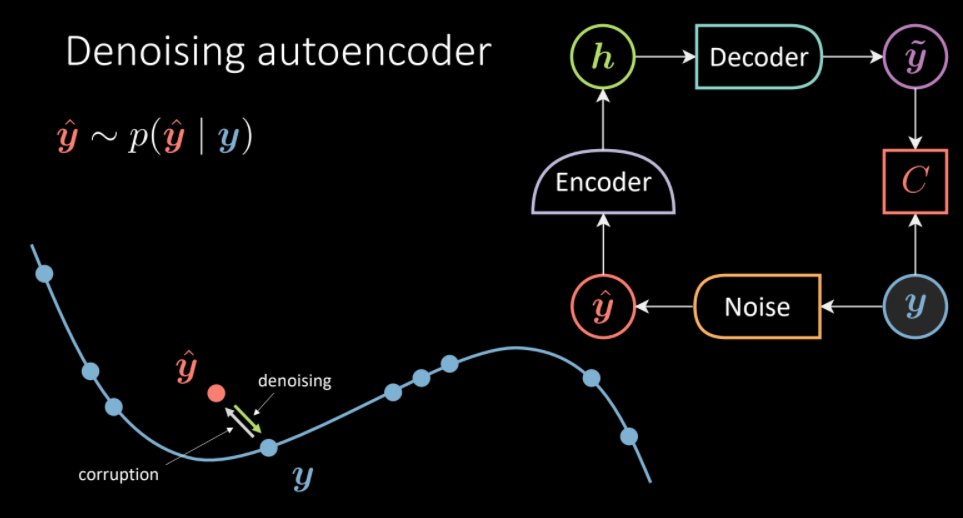
Figure 5 : Architecture de l'auto-encodeur débruiteur. (Intution à gauche, transformer les $\vyhat$ corrompus vers la variété de données de $\vy$)

Dans le but d’ajouter du bruit, nous effectuons les étapes suivantes :

1. Employer do=nn.Dropout() pour désactiver aléatoirement le neurone, c’est-à-dire que certaines valeurs de pixel donneront 0. (L’image originale est composée de valeurs de pixel $[-1,1]$).
2. Créer un masque de bruit en utilisant le dropout do(torch.ones(img.shape)).
3. Générer une image corrompue en multipliant l’image originale avec le masque de bruit. img_bad=(img*noise)

Le critère du modèle reste le même, c’est-à-dire reproduire l’échantillon original à partir d’un échantillon bruité.

Encore une fois, regardons les noyaux de l’encodeur. Comme vous pouvez le voir, il n’y a pas de bruit poivre et sel car la région environnante n’est plus de moyenne zéro et le noyau est obligé d’apprendre à ignorer la région hors d’intérêt.

Figure 6 : Noyaux de l'auto-encodeur débruiteur

Comparaison de notre DAE avec les méthodes d’Inpainting de vision par ordinateur telles que les méthodes Telea et Navier-Stokes.

Bruit
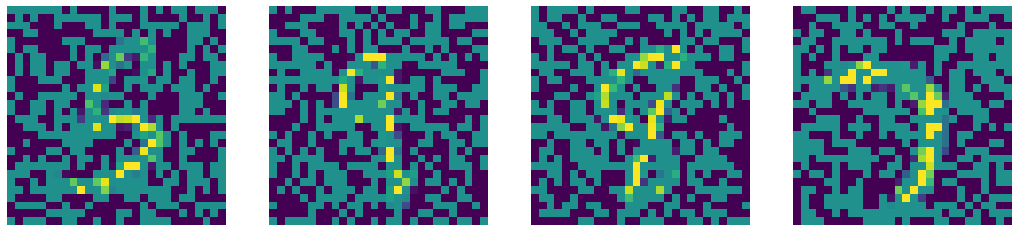
Entrée bruitée
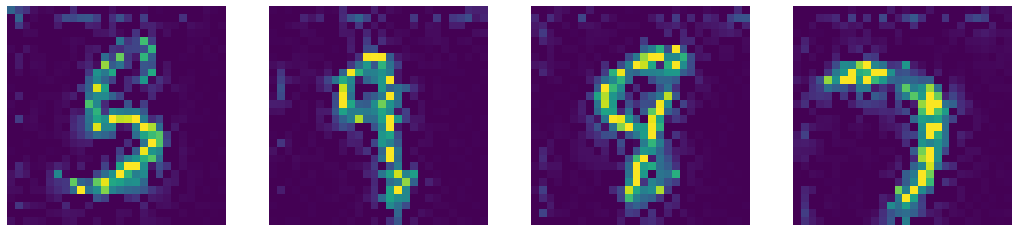
Sortie débruitée par le DAE
Sortie de Telea
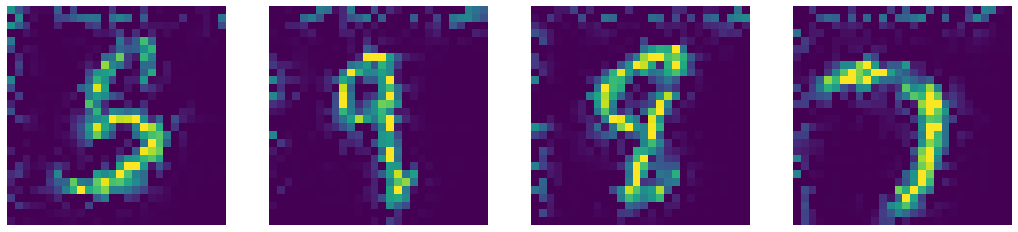
Sortie de Naiver-Stoke
Figure 7 : Comparaison des sorties du DAE et des algorithmes d'inpainting de pointe de vision par ordinateur

Rappelons qu’un DAE est un EBM constrastif qui attribue une faible énergie aux échantillons se trouvant sur la variété de données réel (observé pendant l’entraînement). Maintenant, pour tester cela, nous fusionnons deux chiffres (composite alpha) et passons par l’auto-encodeur :

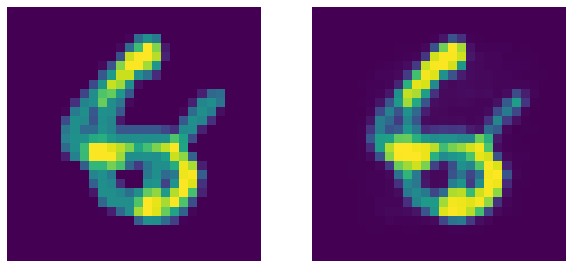
Figure 8 : Chiffres fusionnés à gauche et sortie correspondante du DAE. Le DAE comme prévu ne parvient pas à débruiter l'image (c'est une bonne chose !)

Il est intéressant de noter que l’auto-encodeur ne parvient pas à reconstruire l’entrée des chiffres fusionnées car elle n’a pas été observée pendant l’entraînement. Par conséquent, l’auto-encodeur peut être utilisé pour estimer le degré de bruit d’un échantillon d’entrée donné.

Auto-encodeur variationnel (VAE)

Les auto-encodeurs variationnels sont un type de modèles génératifs où l’on cherche à représenter un attribut latent pour une entrée donnée sous la forme d’une distribution de probabilité. L’encodeur produit $\vmu$ et $\vv$ de sorte qu’un échantillonneur échantillonne une entrée latente $\vz$ à partir de ces sorties d’encodeur. L’entrée latente $\vz$ est simplement introduite dans l’encodeur pour produire $\vyhat$ comme reconstruction de $\vy$.

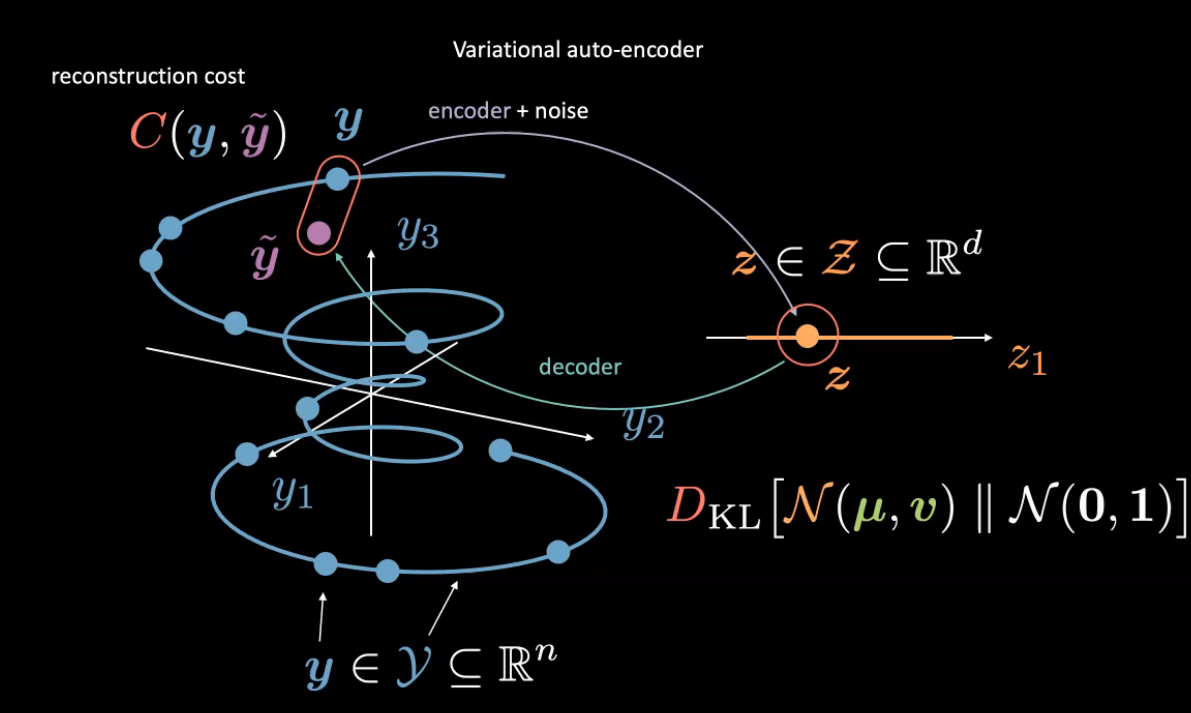
Figure 9 : Intution de l'auto-encodeur variationnel

Ici, nous considérons la variable latente aléatoire $\vz$ appartenant à une gaussienne de moyenne $\vmu$ et de variance $\vy$. (N’hésitez pas à utiliser toute autre distribution). Contrairement à la version précédente, nous ne normalisons pas les images.

Encodeur et décodeur

La dernière couche de l’encodeur a une sortie de dimension $2d$ : les premières valeurs $d$ font référence aux moyennes, $\vmu$ et les dernières valeurs $d$ sont des variances $\vv$. Le décodeur a une activation sigmoïde pour la dernière couche afin de maintenir l’intervalle de sortie $[0,1]$.

d = 20

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

Reparamétrage et fonction forward

Pendant l’apprentissage, la fonction reparameterise est utilisée pour l’astuce de reparamétrage. Nous ne pouvons pas rétropropager à travers l’échantillonneur, nous calculons simplement $\vz=\vmu+\epsilon\odot\sqrt{\vv}$ où $\epsilon \in \orange{\mathcal{N}}(0,\mathbb{I}_d)$. Cela permet de renvoyer le gradient vers l’encodeur. Pendant le test, on utilise simplement $\vmu$.

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        epsilon = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

Nous utilisons la variance logarithmique au lieu de la variance (changement d’échelle) car nous voulons nous assurer que :

1. la variance est non-négative,
2. avoir une gamme complète pour la variance afin de rendre l’entraînement stable.

Rappelons l’énergie libre pour le VAE :

Pour régulariser la variable latente, nous incluons la divergence KL entre la gaussienne de la variable latente et une distribution normale ($\orange{\mathcal{N}}(0,1))$. (Voir également la semaine 8 pour une explication sous forme de bulles de la perte VAE).

Par conséquent, nous définissons la fonction de perte comme suit :

def loss_function(x_hat, x, mu, logvar, β=1):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + β * KLD

Puisque le VAE est un modèle génératif, nous échantillonnons à partir de la distribution pour générer les chiffres suivants :

N = 16
z = torch.rand((N,d))
sample = model.decoder(z)

Figure 10 : Visualisation T-SNE des échantillons générés par le VAE

Les classes sont séparées car le terme de reconstruction force l’espace latent à être bien défini. Les données sont regroupées en classes sans utiliser réellement les étiquettes.

Réseaux antagonistes génératifs (GANs pour Generative Adversarial Networks)

Les GANs ont le même aspect que les DAEs avec quelques modifications. Le DAE implique la génération d’échantillons corrompus à partir de l’entrée et d’une distribution, suivie d’un débruitage à l’aide d’un décodeur. Au lieu de cela, les GANs échantillonnent directement la distribution (sans l’entrée) pour produire une sortie $\vyhat$ en utilisant le générateur (ou décodeur en termes de DAE). Les entrées $\vy$ et $\vyhat$ sont fournies au réseau Cost séparément pour mesurer l’incomptabilité entre elles.

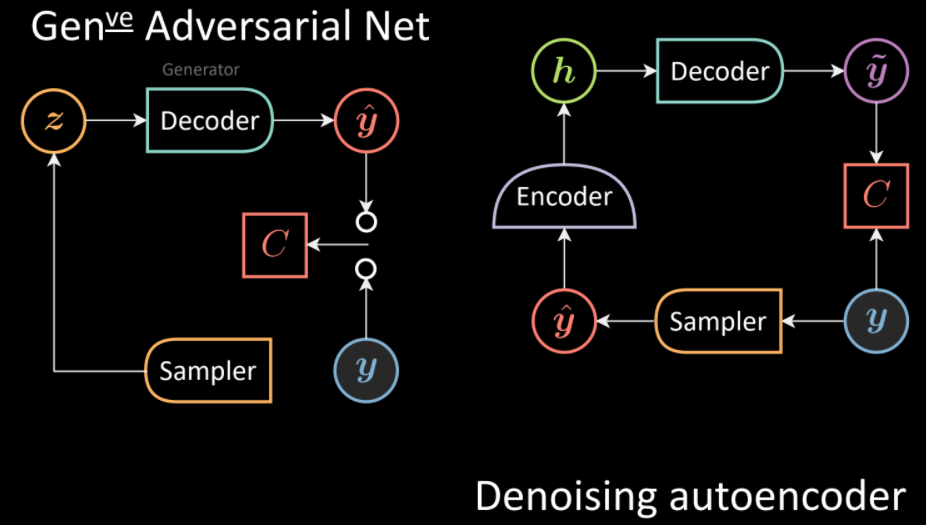
Figure 11 : Comparaison des architectures GANs (à gauche) et DAEs (à droite)

De la même manière, nous pouvons étendre l’analogie avec le VAE. Contrairement au VAE où l’échantillonneur est conditionné à la sortie de l’encodeur, dans les GANs, il y a un échantillonneur non conditionné. Là encore, le décodeur correspond au générateur.

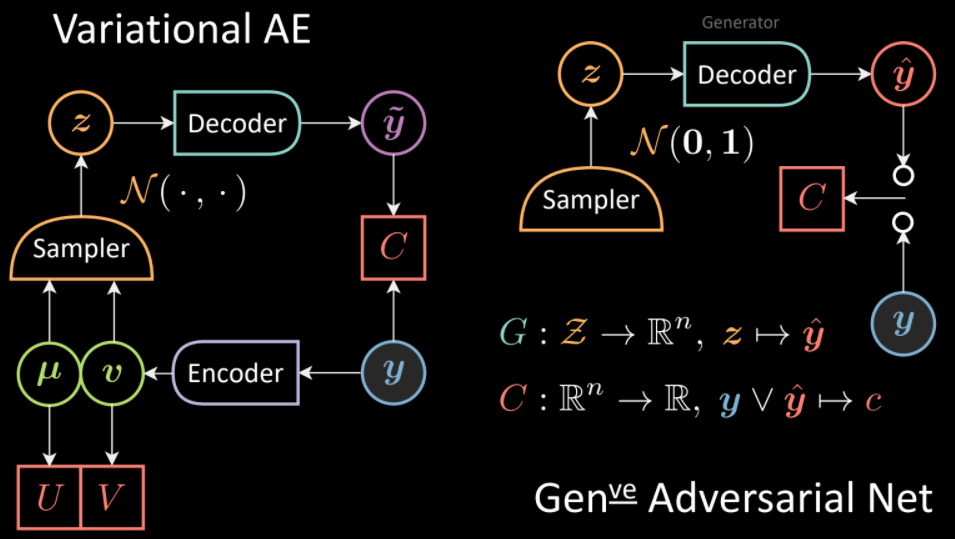
Figure 12 : Comparaison des architectures VAEs (à gauche) et GANs (à droite)

Le générateur fait correspondre l’espace latent à l’espace des données :

Les $\vy$ et $\vyhat$ observés sont introduits dans un réseau de coût pour mesurer l’incompatibilité :

Entraînement des GANs

Nous définissons la fonctionnelle de perte pour le réseau de coût (discriminateur) :

Le but est de diminuer l’échantillon de $\vy$ et d’augmenter l’énergie de $\vyhat$ jusqu’à $m$ (si $\red{C}\geq m$ aucun gradient n’est reçu car $\texttt{ReLU}(\cdot)$ entraînerait la sortie à $0$).

Pour l’entraînement du générateur, l’objectif est simplement de minimiser le coût :

Un choix possible de $\red{C}(\vy)$ peut être :

Le réseau de coût pousse les bons échantillons à 0 et les mauvais échantillons au niveau d’énergie $m$. En utilisant la formule ci-dessus $\red{C}(\vy)$, il existerait une distance quadratique entre les points de la variété $\vy}$ et les points générés par le générateur $\vyhat$. Au cours de l’apprentissage, le générateur est mis à jour pour essayer de produire des échantillons qui auraient progressivement une énergie faible à mesure que $\vy$ est guidé par $\red{C}$. Une fois entraîné, le générateur devrait produire des échantillons proches de la variété de données.

En adoptant une autre analogie, le modèle génératif peut être considéré comme une équipe de faussaires essayant de produire de la fausse monnaie. Leur objectif est de produire de la fausse monnaie qui ne se distingue pas de la vraie. Le disciminateur peut être considéré comme la police qui essaie de détecter les billets de banque contrefaits et faux. Les gradients de la rétropropagation peuvent être considérés comme des espions qui donnent une direction opposée aux contrefacteurs (générateur) afin de tromper la police (discriminateur).

Implémentation de réseaux antagonistes génératifs convolutifs profonds (DCGANs)

Voir ici pour le code complet.

Le générateur suréchantillonne l’entrée en utilisant plusieurs modules nn.ConvTranspose2d pour produire une image à partir d’un vecteur aléatoire nz (bruit).

class Generator(nn.Module):
    def __init__(self, ngpu):
        super(Generator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # l'entrée est Z, elle va dans une convolution
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # la taille de l'état. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # la taille de l'état. (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # la taille de l'état. (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # la taille de l'état. (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # state size. (nc) x 64 x 64
        )

    def forward(self, input):
        if input.is_cuda and self.ngpu > 1:
            output = nn.parallel.data_parallel(self.main, input, range(self.ngpu))
        else:
            output = self.main(input)
        return output

Le discriminateur est essentiellement un classifieur d’images qui utilise nn.Sigmoid() pour classer l’entrée comme vraie/fausse.

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # l'entrée est (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # la taille de l'état. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # la taille de l'état. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # la taille de l'état. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # la taille de l'état. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

Nous utilisons l’entropie croisée binaire pour entraîner les réseaux.

criterion = nn.BCELoss()

Nous avons deux optimiseurs pour chaque réseau. Nous voulons augmenter l’énergie des mauvais échantillons (images fausses reconnaissables) et diminuer l’énergie des bons échantillons (images réelles).

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

Pour l’entraînement, nous entraînons d’abord le discriminateur avec des images réelles et des étiquettes indiquant que les images sont réelles. Ensuite, nous générons de fausses images à partir de bruit. Le discriminateur est à nouveau entraîné, mais cette fois avec des images fausses et des étiquettes indiquant qu’elles sont fausses.

# Cette partie est à l'intérieur de la boucle d'entraînement !
        # entraîner avec les vraies
        netD.zero_grad()
        real_cpu = data[0]
        batch_size = real_cpu.size(0)
        label = torch.full((batch_size,), real_label,
                           dtype=real_cpu.dtype)

        output = netD(real_cpu)
        errD_real = criterion(output, label)
        errD_real.backward()
        D_x = output.mean().item()

        # entraîner avec les fausses
        noise = torch.randn(batch_size, nz, 1, 1,)
        fake = netG(noise)
        label.fill_(fake_label)
        output = netD(fake.detach())
        errD_fake = criterion(output, label)
        errD_fake.backward()
        D_G_z1 = output.mean().item()
        errD = errD_real + errD_fake
        optimizerD.step()

Pour entraîner le générateur, nous calculons l’erreur par incompatibilité entre les caractéristiques de l’image réelle et de l’image fausse telles qu’identifiées par le discriminateur. De sorte que le générateur puisse utiliser cette mesure d’incompatibilité pour mieux tromper le discriminateur.

# Cette partie est à l'intérieur de la boucle d'entraînement !
        netG.zero_grad()
        label.fill_(real_label)  #les faux labels sont réels pour le coût du générateur
        output = netD(fake)
        errG = criterion(output, label)
        errG.backward()
        D_G_z2 = output.mean().item()
        optimizerG.step()