Modèles génératifs / Auto-encodeurs

Récapitulation : Modèle prédictif à variables latentes

Les variables latentes sont utiles pour fournir des informations supplémentaires qui aident à prédire plusieurs valeurs de la cible $\vy$, associées à l’entrée $\cx$. Nous avons vu précédemment que pour prédire la variable cible $\vy$ à partir de la variable latente $\cz$, la fonction d’énergie est donnée comme suit :

Pour être clair, nous montrons l’unité de $\boldsymbol{g}$ :

Dans ce cas la variable latente $\cz$ est unidimensionnelle. Cependant, si la $\vz$ a une dimension plus élevée, cela pourrait conduire à une fonction d’énergie de $0$ partout. Par conséquent, afin de garantir des valeurs d’énergie plus faibles pour des prédictions plus compatibles, nous introduisons un facteur régularisé.

Récapitulatif de l’entraînement

Étant donné une observation $\vy$, l’entraînement du modèle à variable latente régularisée,

où $\vytilde = \Dec(\vz)$,

on calcule

et on minimise

A la limite vers zéro de la température, on calcule

et on minimise

Propagation de la cible

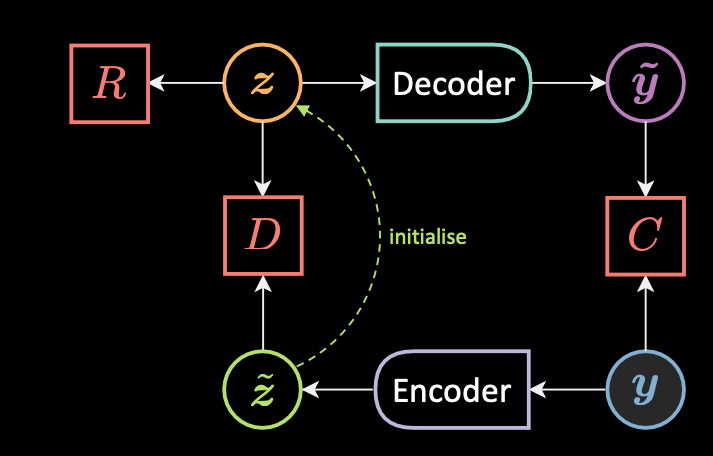
Figure 1 : Propagation de la cible

La figure 1 montre l’architecture de la propagation de la cible. Étant donné une observation $\vy$, nous calculons d’abord $\vztilde$ qui est la supposition initiale de la variable latente $\vz$.

Nous initialisons ensuite $\vz$ à $\vztilde$, ici nous devons nous assurer que ces valeurs ne sont pas trop éloignées les unes des autres.

Nous minimisons maintenant la fonctionnelle de perte en deux étapes, en minimisant $\mathcal{L}(\red{F}_{\infty}(\cdot), \vect{\blue{Y}})$ :

De cette façon, $\vz$ est contraint de ne prendre qu’un ensemble de valeurs.

Auto-encodeur (AE)

Un auto-encodeur est un type de réseau neuronal artificiel utilisé pour apprendre des codages de données efficaces de manière non supervisée. L’objectif est d’abord d’apprendre des représentations codées de nos données, puis de générer les données d’entrée (aussi étroitement que possible) à partir des représentations codées apprises. Ainsi, la sortie d’un auto-encodeur est sa prédiction pour l’entrée.

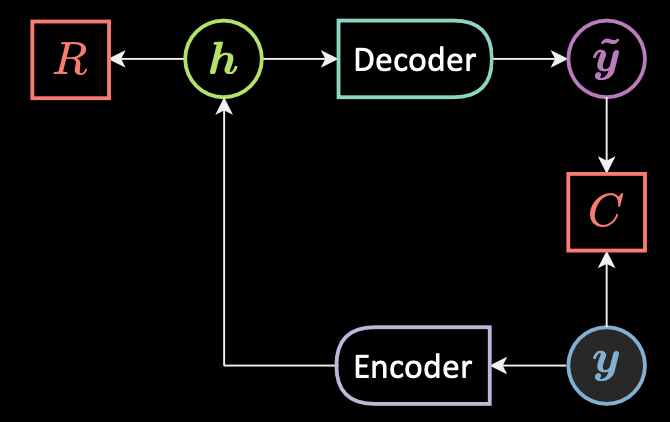
Figure 2 : Architecture d'un auto-encodeur de base.

La figure 2 montre l’architecture d’un auto-encodeur de base. Pour résumer à un haut niveau, une forme très simple d’AE est la suivante :

• Tout d’abord, l’auto-encodeur reçoit une entrée et l’applique à un état caché par le biais d’une transformation affine $\vh = f(\mW{_h} \vy + \vb{_h})$, où $f$ est une fonction d’activation (par éléments). Il s’agit de l’étape encodeur. A noter que $\vh$ est également appelé le code.
• Ensuite, $\vytilde = g(\mW{_y} \vy + \vb {_y})$, où $g$ est une fonction d’activation. C’est l’étape du décodeur.
• Enfin, l’énergie est la somme de la reconstruction et de la régularisation : $\red{F}(\vy) = \red{C}(\vy,\vytilde)+ \red{R}(\vh)$.

Coûts de reconstruction

Lorsque l’entrée est à valeur réelle, nous utilisons la perte d’erreur quadratique moyenne :

Lorsque l’entrée est catégorique, nous utilisons la perte d’entropie croisée :

Fonctionnel de perte

La fonctionnelle de perte est la moyenne de la perte par échantillon :

Couche cachée sous-complète ou sur-complète

Lorsque la dimensionnalité de la couche cachée est inférieure à la dimensionnalité de l’entrée, la couche cachée est incomplète. Lorsque la dimensionnalité de la couche cachée est supérieure à la dimensionnalité de l’entrée, elle est surcomplète. La dimensionnalité de la couche cachée est plus grande que celle de l’entrée afin qu’elles puissent être linéairement séparables. Cependant, cela peut conduire à une représentation effondrée. En effet, en reconstruisant l’entrée, le modèle peut copier toutes les caractéristiques. Afin d’éviter cela, il existe quelques techniques telles que l’auto-encodeur débruiteur, l’auto-encodeur contractif, l’auto-encodeur variationnel, etc.

L’auto-encodeur débruiteur (DAE de l’anglais denoising auto-encodeur)

L’auto-encodeur débruiteur est une technique contrastive. La figure 3 ci-dessous montre l’architecture et la variété du DAE ainsi que l’intuition de son fonctionnement.

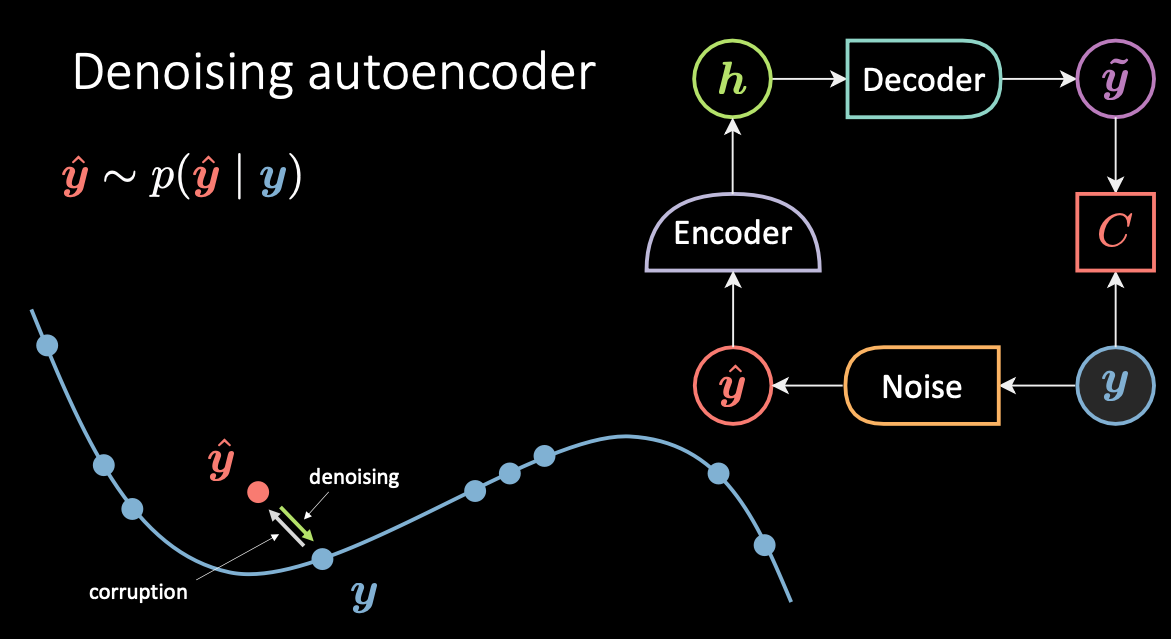
Figure 3 : L'auto-encodeur débruiteur

Dans ce modèle, on corrompt la donnée d’entrée $\vy$ en bleu (car elle est froide / a une énergie faible), et on obtient l’échantillon $\vyhat$ en rouge (car il est chaud / a une haute énergie). L’énergie associée à $\vytilde$ est la distance euclidienne au carré par rapport à sa valeur initiale. Ensuite, $\vytilde$ est ré-encodé dans la variable cachée $\vh$ puis repassé au décodeur produisant $\vytilde$ qui doit être proche de la cible$\vy$. Par conséquent, quel que soit le bruit ajouté aux données originales, l’auto-encodeur doit apprendre à séparer le bruit et à retrouver la valeur originale de $\vy$.

L’auto-encodeur contractif (CAE de l’anglais contractive auto-encodeur)

Un auto-encodeur contractif est une technique d’apprentissage profond non supervisé qui aide un réseau neuronal à encoder des données d’entraînement non étiquetées. Il rend cet encodage moins sensible aux petites variations de son ensemble de données d’apprentissage. Pour ce faire, un régulariseur ou terme de pénalité, est ajouté au coût ou à la fonction objective que l’algorithme tente de minimiser. Le résultat final est de réduire la sensibilité de la représentation apprise envers l’entrée d’entraînement.

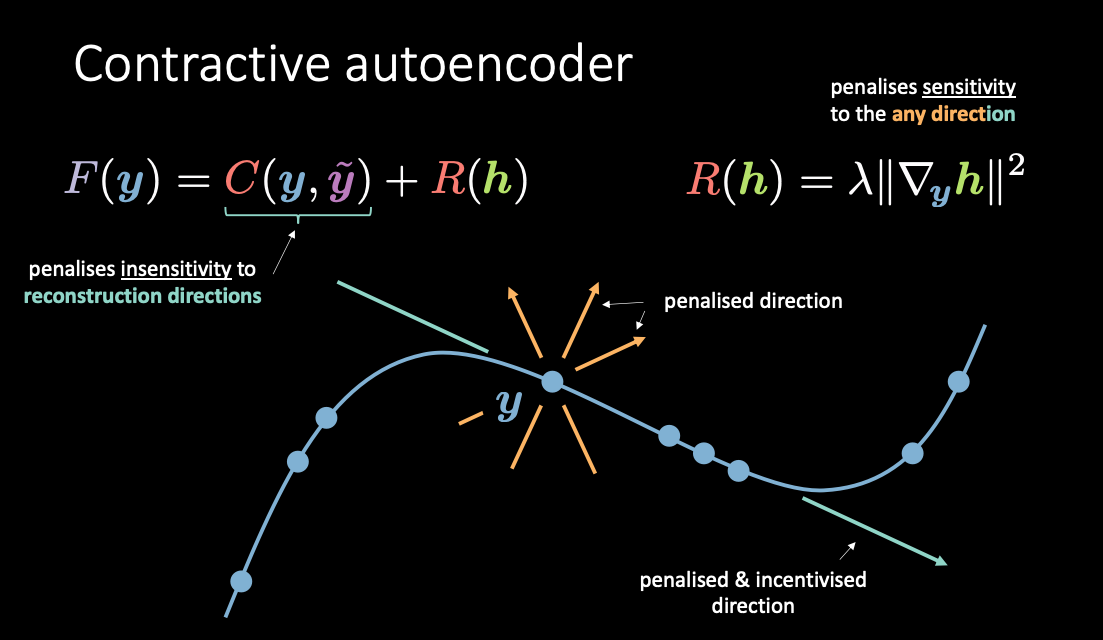
Figure 4 : L'auto-encodeur contractif

Comme le montre la figure 4, $\red{C}(\vy, \vytilde)$ pénalise les sensibilités aux reconstructions le long de la variété tandis que $\red{R}(\vh)$ pénalise combien le remuement de $\vh$ provient du remuement de $\vy$. De cette manière, on peut augmenter les énergies uniquement dans les directions qui ne sont pas utilisées pour la reconstruction.

L’auto-encodeur variationnel (VAE de l’anglais variational auto-encodeur)

Intuition derrière les VAEs et comparaison avec les auto-encodeurs classiques

Nous présentons les auto-encodeurs variationnels, un type de modèle génératif. Mais pourquoi s’intéresser aux modèles génératifs ? Pour répondre à la question, les modèles discriminatifs apprennent à faire des prédictions à partir de certaines observations, mais les modèles génératifs visent à simuler le processus de génération de données. L’un des effets est que les modèles génératifs peuvent mieux comprendre les relations causales sous-jacentes, ce qui conduit à une meilleure généralisation.

Quelle est la différence entre un auto-encodeur variationnel (VAE) et un auto-encodeur de base (AE) ?

Bien que le nom VAE comporte le terme auto-encodeur, en raison de la similitude structurelle ou architecturale avec les auto-encodeurs, les formulations entre VAE et AE sont très différentes. La figure 5 ci-dessous montre les architectures des VAEs et des AEs de base.

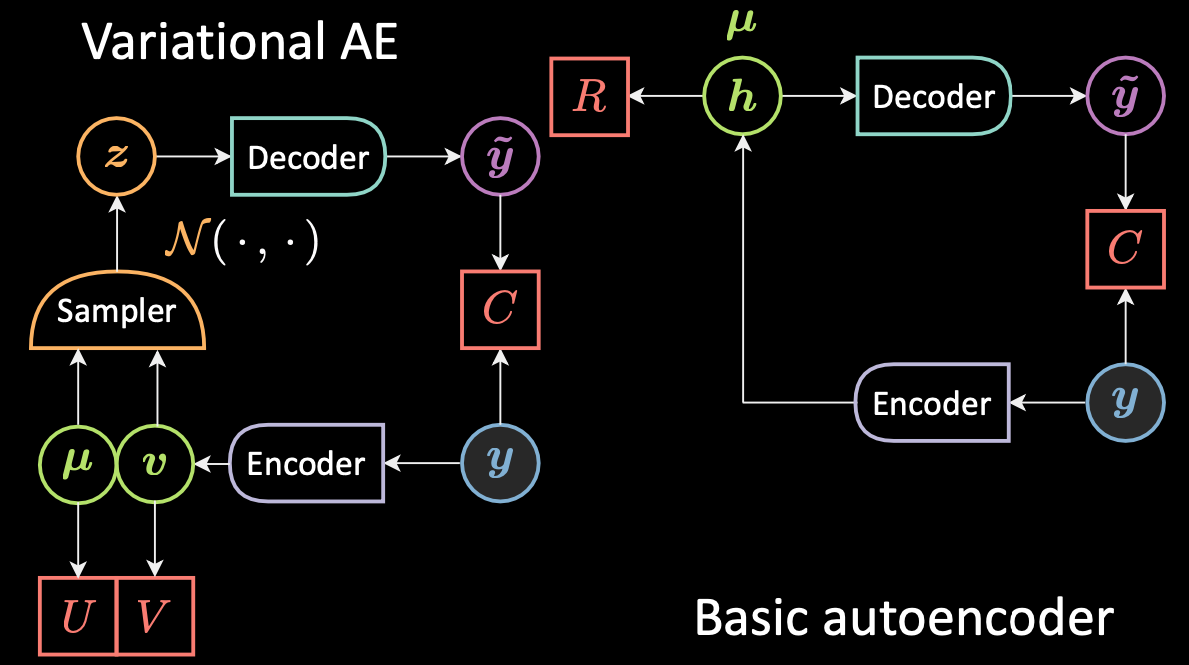
Figure 5 : VAE vs AE de base

Pour un VAE :

• Premièrement l’étape de l’encodeur : on passe l’entrée $\vy$ à l’encodeur. Au lieu de générer une représentation cachée $\vh$ comme pour l’AE, la représentation cachée dans le VAE comprend deux parties : $\vmu$ et $\vv$. De la même manière que nous utilisons le facteur de régularisation $\red{R}$ pour $\vh$, nous utilisons les facteurs de régularisation $\red{U}$ et $\red{V}$ pour $\vmu$ et $\vv$,respectivement.
• Ensuite, nous utilisons un échantillonneur pour échantillonner $\vz$ qui est la variable aléatoire latente suivant une distribution gaussienne $\vmu$ et $\vv$. A noter qu’en pratique les gens utilisent les distributions gaussiennes comme distribution codée mais d’autres distributions peuvent également être utilisées.
• Enfin, $\vz$ est passé dans le décodeur pour générer $\vytilde$.
• Le décodeur sera une fonction de $\orange{\mathcal{Z}}$ à $\mathbb{R}^{n}$ : $\vz \mapsto \vytilde$.

En fait, pour un auto-encodeur de base, nous pouvons considérer que $\vh$ est simplement le vecteur $\vmu$ dans la formulation VAE avec la variance fixée à zéro. En bref, la principale différence entre les VAEs et les AEs est que les VAEs ont un bon espace latent qui permet un processus génératif.

Quelle est la différence entre l’auto-encodeur variationnel (VAE) et l’auto-encodeur débruiteur (DAE) ?

Comparons maintenant la différence entre VAE et DAE avec la figure 6 ci-dessous.

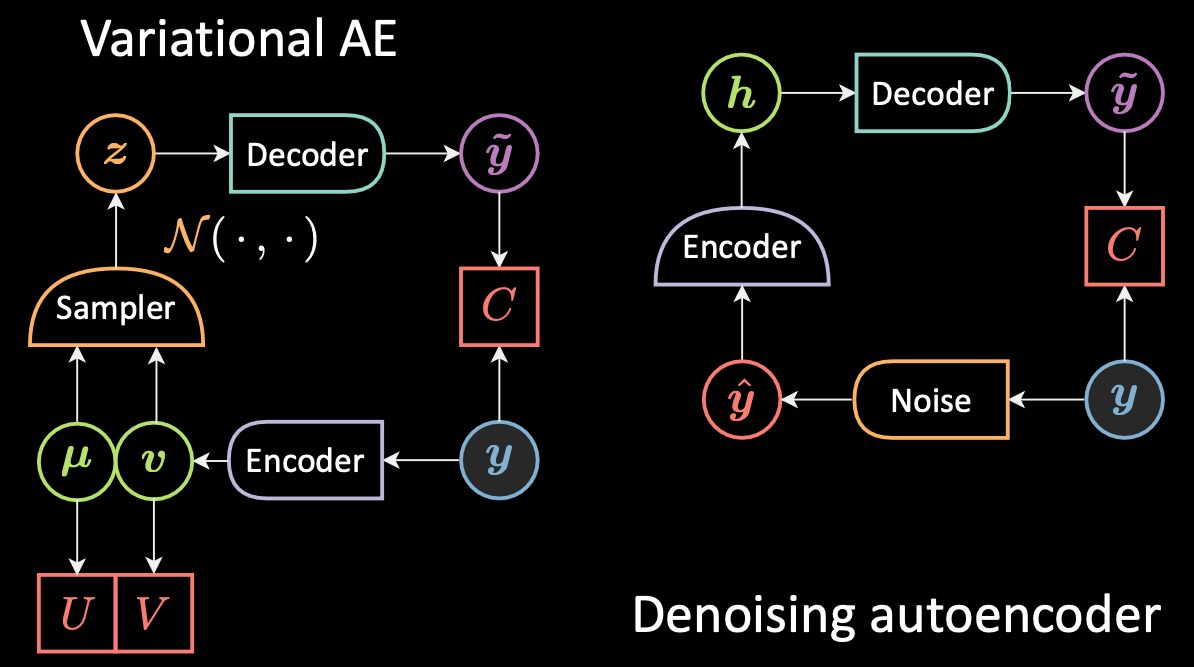
Figure 6 : VAE vs DAE

Pour le DAE, comme nous l’avons mentionné précédemment, l’échantillonnage se produisait entre $\vy$, en bleu car il est froid / a une énergie basse, et $\vyhat$ en rouge car il est chaud / a une haute énergie. On déplace donc l’entrée et on décode tout en $\vytilde$. Pour le VAE, on code l’entrée et on ajoute du bruit dans la cachée ainsi on change plus ou moins la position de l’encodeur dans l’échantillonneur.

La fonction objectif du VAE

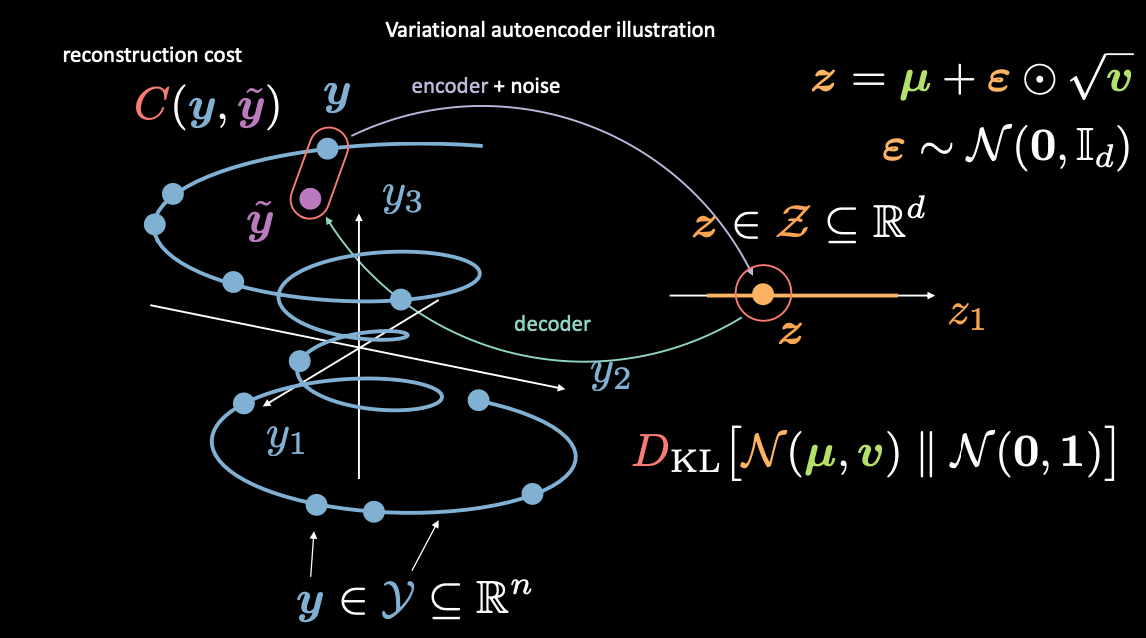
Figure 7 : Association de l'espace d'entrée à l'espace latent

Tout d’abord, nous codons de l’espace d’entrée (à gauche) à l’espace latent (à droite), en passant par l’encodeur et le bruit. Ensuite, nous décodons de l’espace latent (droite) vers l’espace de sortie (gauche). Pour passer de l’espace latent à l’espace d’entrée (le processus génératif), nous devons soit apprendre la distribution (du code latent), soit imposer une certaine structure. Dans notre cas, le VAE impose une certaine structure à l’espace latent.

Comme d’habitude, pour entraîner le VAE nous minimisons une fonction de perte. La fonction de perte est donc composée d’un terme de reconstruction ainsi que d’un terme de régularisation.

• Le terme de reconstruction se trouve sur la dernière couche (côté gauche de la figure). Cela correspond à $\red{C}(\vy, \vytilde)$ dans la figure.
• Le terme de régularisation se trouve sur la couche latente, afin d’imposer une structure gaussienne spécifique à l’espace latent (côté droit de la figure). Pour ce faire, nous utilisons un terme de pénalité $\red{D}_{KL}(\orange{\mathcal{N}}(\vmu, \vv) \mathrel{\Vert} \orange{\mathcal{N}}(\boldsymbol{0}, \boldsymbol{1}))$. Sans ce terme, le VAE agira comme un AE de base, ce qui peut conduire à un surentraînement et nous n’aurons pas les propriétés génératives que nous souhaitons.

Discussion sur l’échantillonnage de $\vz$ (astuce de reparamétrisation)

Comment ajouter ce bruit comme mentionné ci-dessus ? Nous introduisons ici l’astuce de reparamétrisation. D’après ce qui précède, nous savons que nous échantillonnons à partir de la distribution gaussienne pour obtenir la variable latente $\vz$. Cependant, cela pose problème car lorsque nous effectuons la descente de gradient pour entraîner le VAE, nous ne savons pas comment effectuer la rétropropagation à travers le module d’échantillonnage.

Nous pouvons simplement dire que la nouvelle latente $\vz$ sera $\vmu$ qui est l’estimation de la moyenne plus un epsilon qui a été échantillonné à partir d’une gaussienne dont l’amplitude est modifiée par la racine carrée de l’écart type $\vv$. Ainsi, de cette manière, nous pouvons faire circuler les gradients dans ces encodeurs.

Visualisation des estimations des variables latentes et perte de reconstruction

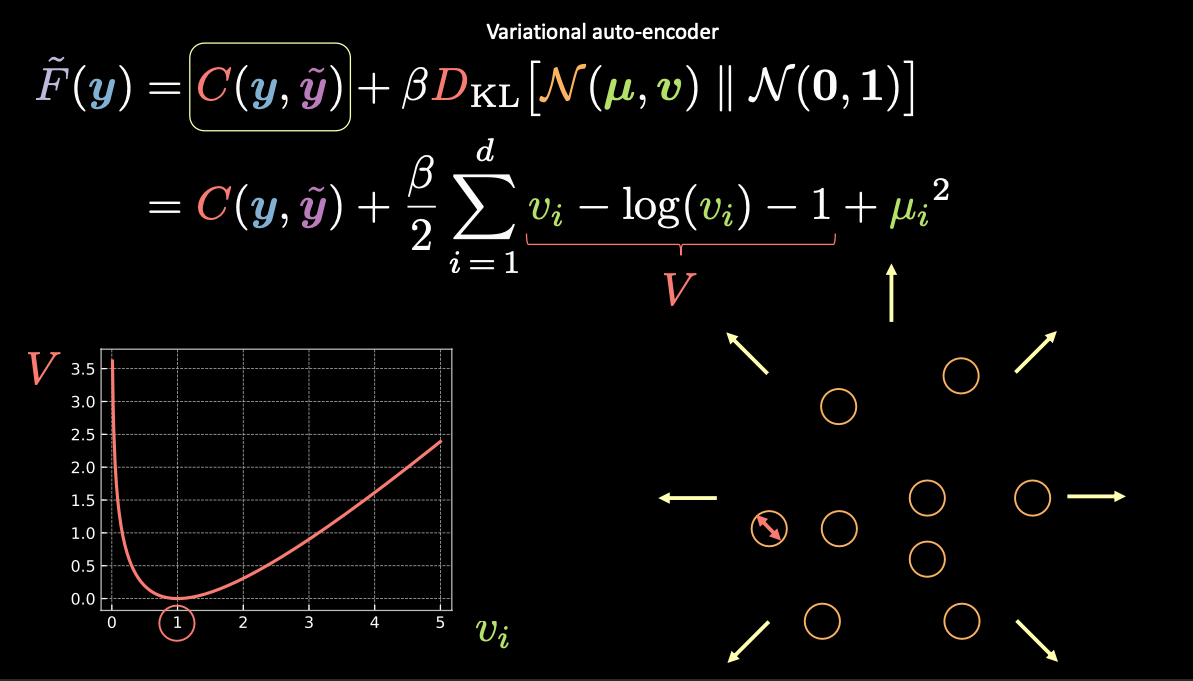
Figure 8 : Visualisation du vecteur $z$ sous forme de bulles dans l'espace latent

Dans la figure 8 ci-dessus, chaque bulle représente une région estimée de $\vz$ et les flèches représentent la façon dont le terme de reconstruction éloigne chaque valeur estimée des autres, ce qui est expliqué plus en détail ci-dessous.

Comme indiqué ci-dessus, l’énergie libre pour le VAE contient deux termes : un terme de reconstruction et un terme de régularisation. Nous pouvons l’écrire comme suit :

Pour visualiser l’objectif de chaque terme de l’énergie libre, nous pouvons considérer chaque valeur estimée de $\vz$ comme un cercle dans l’espace $2D$, où le centre du cercle est $\vmu$ et la zone environnante sont les valeurs possibles de $\vz$ déterminées par $\vv$.

S’il existe un chevauchement entre deux estimations de $\vz$ (visuellement si deux bulles se chevauchent), cela crée une ambiguïté pour la reconstruction car les points du chevauchement peuvent être mis en correspondance avec les deux entrées originales. Le premier terme $\red{C}(\vy, \vytilde)$ force à reconstruire ces bulles aux emplacements corrects.

• La perte de reconstruction $\red{C}(\vy, \vytilde)$ éloignera les points l’un de l’autre de sorte qu’il n’y ait pas de chevauchement.
• Une autre option pour $\red{C}(\vy, \vytilde)$ pour éviter le chevauchement est de rendre la variance nulle et alors il n’y a que des points autres que les bulles donc il n’y a plus de chevauchement.

Cependant, si nous utilisons uniquement la perte de reconstruction, les estimations continueront à s’éloigner les unes des autres et le système pourrait exploser. C’est là que le terme de pénalité entre en jeu.

Le terme de pénalité

Le deuxième terme est l’entropie relative (une mesure de la distance entre deux distributions) entre une gaussienne de moyenne $\vmu$ et de variance $\vv$, et la distribution normale standard. Si nous développons ce deuxième terme dans la fonction de perte VAE, nous obtenons :

où l’expression dans la sommation a quatre termes.

Utilisons $\red{V}$ pour les trois premiers termes.

D’après le graphique en bas à gauche de la figure 8 ci-dessus, nous pouvons voir que cette expression est minimisée lorsque $\green{v_i}$ est égal à 1. Par conséquent, notre perte de pénalité maintiendra la variance de nos variables latentes estimées autour de 1. Visuellement, cela signifie que nos “bulles” du dessus auront un rayon d’environ 1.

Le dernier terme, $\green{\mu_i}^2$, minimise la distance entre les bulles et empêche donc l’“explosion” encouragée par le terme de reconstruction.

Note : le $\beta$ dans la fonction de perte VAE est un hyperparamètre qui dicte la manière de pondérer les termes de reconstruction et de pénalité.