图形卷积网络 III

图形卷积网络(英文简称GCN)

图形卷积网络是一种使用数据结构的架构。在说得更深入一点前，让我们快速地回顾一下自我注意力机制，如图形卷积网络和自我注意力机制都是埋论上一样的。

回顾一下: 自我注意力机制

在自我注意力机制中，我们有一个输入集$\lbrace\boldsymbol{x}_{i}\rbrace^{t}_{i=1}$。不像序列那样，它没有顺序的。 隐藏向量$\boldsymbol{h}$是由集之中的向量的线性组合得出来的。 我们可以用矩阵向量乘法来以$\boldsymbol{X}\boldsymbol{a}$去表达这个东西，这里$\boldsymbol{a}$包含一些会缩放向量$\boldsymbol{x}_{i}$的系数。

如果想要更多深入的解释，请看第12个星期的笔记。

符号

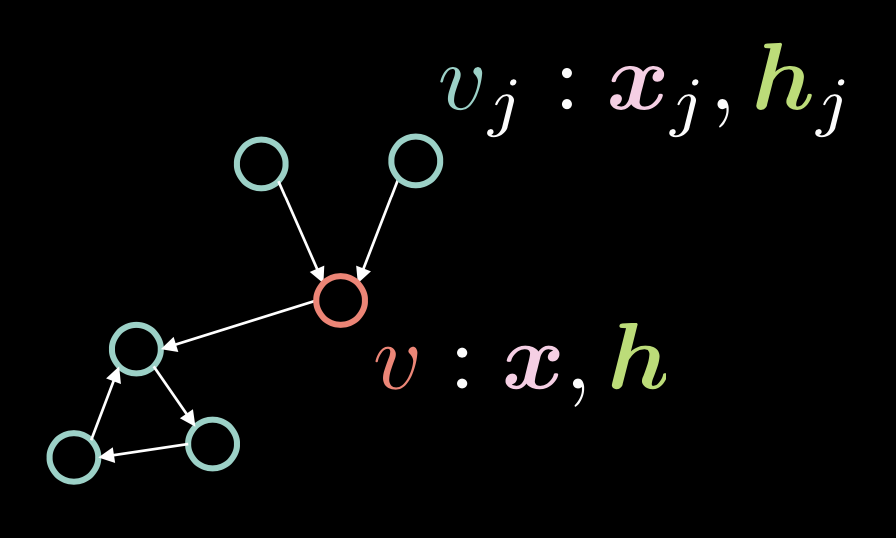
图 1: 图形卷积网络

在图1，顶点$v$包含两个向量:输入$\boldsymbol{x}$和它的隐蔽表示$\boldsymbol{h}$。我们也有多个顶点$v_{j}$，它們包含$\boldsymbol{x}_j$ 和 $\boldsymbol{h}_j$。在这个图形，顶点都是以有向边来连接起来。

我们以邻接向量$\boldsymbol{a}$来代表这些有向边，这里如果是一个有向边由$v_{j}$到$v$的话，那每一个元件$\alpha_{j}$都设定为$1$。

度数$d$，也就是连接入来的边的数量是多少来决定度数，而它是以一个邻接向量的范数来定义出来，比如$\Vert\boldsymbol{a}\Vert_{1} $，也就是在向量$\boldsymbol{a}$中有多少个一。

而隐藏向量$\boldsymbol{h}$是以这个表达式来表逹:

这里$f(\cdot)$是一个非线性函数，比如修正线性单元英文为ReLU，符号为$(\cdot)^{+}$，而S形函数的符号为$\sigma(\cdot)$，而双曲正切的符号为$\tanh(\cdot)$。

这个$\boldsymbol{U}\boldsymbol{x}$项是要用在顶点$v$上，就是对输入$v$用上这个旋转$\boldsymbol{U}$。

记得在自我注意力机制中，隐藏向量$\boldsymbol{h}$是以$\boldsymbol{X}\boldsymbol{a}$来计算出来， 也就是说在$\boldsymbol{X}$中的行是以在$\boldsymbol{a}$中的因素缩放出来的。而图形卷积网络的内容中， 这意思着这样，如果我们有多个由外传入来的边，比如在邻接向量$\boldsymbol{a}$中有多个1，$_boldsymbol{X}_boldsymbol{a}$就会变得很大。 在另一面，如果我们只有一个传入来的边，这个值就会变得很细。 去补救这个数值与由外传入来的边是成比例的问题，我们对它除以一个数， 这个数就是由外传入来的边有多少的数量，这个数叫$d$。我们之后对$_boldsymbol{X}_boldsymbol{a}d^{-1}$使用一个旋转$_boldsymbol{V}$。

我們可以以這個隱藏表示$\boldsymbol{h}$來以下方的矩陣符號來表達整個輸入集$\boldsymbol{x}$

where $\vect{D} = \text{diag}(d_{i})$.

残差门控式图形卷积网络理论和代码

残差门控式图形卷积网络是一种图形卷积网络，也可以以图2来表示出来:

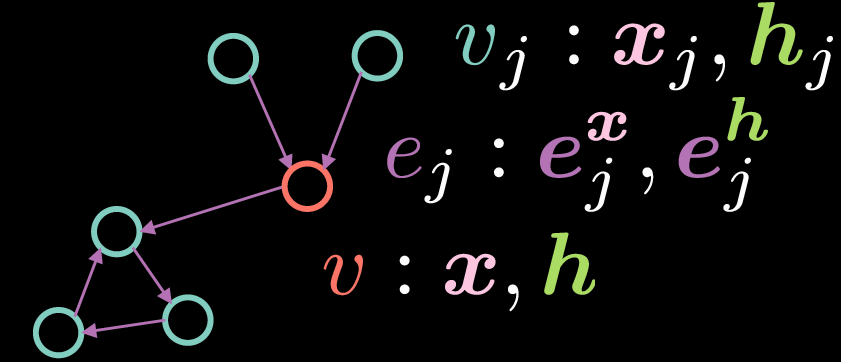
图 2: 残差门控式图形卷积网络

以一個標準的圖形卷積网絡，頂點$v$由這兩個向量組成:輸入$\boldsymbol{x}$和它的隱藏表示$\boldsymbol{h}$。相反，在這個例子，邊都有一個特徵表示，而這裡的$\boldsymbol{e_{j}^{x}}$ 代表著一個輸入邊表示和$\boldsymbol{e_{j}^{h}}$代表一個隱藏邊表示。

就如基本型图形卷积网络，顶点$v$由两个向量组成:输入x和它的隐藏表示$\boldsymbol{h}$ 。

这里$\boldsymbol{x}$是一个输入表示，而$\boldsymbol{Ax}$代表对输入$\boldsymbol{x}$用上了一个旋转，而且$\sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}}$表示一个已旋转了的传入来的特征$\boldsymbol{Bx_{j}}$和门$\eta(\boldsymbol{e_{j}})$的逐元素乘法，然后最后就来一个总结。和标准的图形卷积网络比较，上方的就会对传入来的表示进行平均值运算，而门控项是对实作残差门控式图形卷积网络来说是最重要的，因为它容许我们去调节传入来的基于边的表示。

注意到的是总和只是总和所有顶点${v_j}$，而这些顶点都有传入来的边连到顶点${v}$。而在残差门控式图形卷积网络中的项:「残差」，这个项事实上来自一个做法，如果要计算出隐藏$\boldsymbol{h}$，我们就要加那个输入表示$\boldsymbol{x}$。而那个门项$\eta(\boldsymbol{e_{j}})$是以下方那样来计算:

而门数值$\eta(\boldsymbol{e_{j}})$是归一化后的S型函数，取得它的方法是这样的:先把所有传入来的边的表示每一个进行S型函数，然后加起来，最后就是对所有传入来的边的表示进行了S型函数后除以刚刚加好的数。注意的是，为了计算门项，我们要边$\boldsymbol{e_{j}}$的表示，也就可能会被这样计算出来，以以下的方程式:

这个隐藏的边表示$\boldsymbol{e_{j}^{h}}$是由总和初始边缘表示$\boldsymbol{e_{j}^{x}}$和$\texttt{ReLU}(\cdot)$所得到，这里的修正线性单元$\texttt{ReLU}(\cdot)$，就是用在$\boldsymbol{e_{j}}$。而$\boldsymbol{e_{j}}$就是由总和所有这些东西们: 1. 用在$\boldsymbol{x_{j}}$上的旋转﹑2.一个用在顶点$v_{j}$的输入表示xj的旋转﹑3.一个用在顶点$v$的输入表示 $\boldsymbol{x}$的旋转。

注意: 为了计算出低层的隐藏表示(比如说$2^\text{nd}$层的隐藏表示)，我们可以在上方的方程式简单地更换输入特征表示为$1^\text{st}$层特征表示。

图形分类和残差门控式图形卷积网络的层

在这个部份，我们介绍了图形分类问题和写残差门控式图形卷积网络的代码的层。不单止一般也要的汇入们，我们也加这些:

os.environ['DGLBACKEND'] = 'pytorch'
import dgl
from dgl import DGLGraph
from dgl.data import MiniGCDataset
import networkx as nx

第一行令DGL去用Pytorch作为后端。深度图形函式库(DGL)在图形们上提供各式各样的功能，而networkx容许我们去视觉地看明明这些图形。

在这个笔记本，任务是去分类出一个给予的图形结构为8种不同的图形的其中之一。而利用min_num_v和max_num_v之间的节点去在dgl.data.MiniGCDataset得到的数据集，就会给出一些图形的数字(num_graphs)。所以，所有得到的图形不会有同样的节点或顶点的数字。

为了使您熟悉DGLGraphs的基础知识，建议您阅读這个简短的教程

创造这个图形后，下一步就是在域中加一些信号。特征可以被加到去节点和DGLGraph的边。而特征是以名字（字符串）和张量（字段，英文field）。 ndata和edata都是语法糖来访问所有节点和边的特征数据。

而接下来的代码片段显示出特征如何生成出来。而每一个节点都设有一个数值，这数值等于有多少条和别的节点连起来的连接边(incident edges)，这里每一条边的数值设为1。

def create_artificial_features(dataset):
    for (graph, _) in dataset:
        graph.ndata['feat'] = graph.in_degrees().view(-1, 1).float()
        graph.edata['feat'] = torch.ones(graph.number_of_edges(), 1)
    return dataset

训练用的数据集和测试用的数据集都被创造出来，而特征都被设为下方那样:

trainset = MiniGCDataset(350, 10, 20)
testset = MiniGCDataset(100, 10, 20)

trainset = create_artificial_features(trainset)
testset = create_artificial_features(testset)

一个来的训练集的图形就有以下的设定。这里，我们看到图形有15个节点和45条边，而且两个节点和边都有如预期那样大小为(1, )的特征表示。而且，这个0表示这个图形是属于第0类。

(DGLGraph(num_nodes=15, num_edges=45,
         ndata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}
         edata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}), 0)

有关DGL信息的笔记和降低函数

在DGL，信息函数们都被表达为边UDFs (使用者定义出来的函数)。边UDFs会接收一个单一的实参edges。它有3个东西:src和dst﹑data。这三个东西都对应地用来访问源头节点的特征和目的地节点的特征﹑边的特征。这个降低函数都是节点UDFs。节点UDFs有一个实参node(节点)，也就是有两个东西data和mailbox。对应着第二个维度来堆起来(所以这里是dim=1)，那data就包含的节点特征和mailbox就包含所有由外入来的信息特征。而这个函数update_all(message_func, reduce_func)会发送所有信息连过所有边，然后更新所有节点。

门控式残剩图形卷积网络的层的实作

一个门控式残剩图形卷积网络的层的实行就如以下的代码所示。

第一，所有的输入特征的旋转$\boldsymbol{Ax}$和$\boldsymbol{Bx_{j}}$﹑$\boldsymbol{Ce_{j}^{x}}$﹑$\boldsymbol{Dx_{j}}$﹑$\boldsymbol{Ex}$都是以在__init__定义出来的nn.Linear的层们计算出来的，之后就是对输入表示h和e由在forward 函數中的线性层(英文linear layers)中进行前向传播。

class GatedGCN_layer(nn.Module):

    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.A = nn.Linear(input_dim, output_dim)
        self.B = nn.Linear(input_dim, output_dim)
        self.C = nn.Linear(input_dim, output_dim)
        self.D = nn.Linear(input_dim, output_dim)
        self.E = nn.Linear(input_dim, output_dim)
        self.bn_node_h = nn.BatchNorm1d(output_dim)
        self.bn_node_e = nn.BatchNorm1d(output_dim)

第二，我们计算这个边表示。这是在message_func函数中完成的，也就对所有边进行迭代，同时去计算边的特征。特别地，这条线e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']在上方那里计算出来(方程式7)。而这个message_func函数送这个Bh_j(也就是方程式5的$\boldsymbol{Bx_{j}}$ )和这个e_ij(方程式7)，通过边，送到目的地节点的邮箱。

def message_func(self, edges):
    Bh_j = edges.src['Bh']
    # e_ij = Ce_ij + Dhi + Ehj
    e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']
    edges.data['e'] = e_ij
    return {'Bh_j' : Bh_j, 'e_ij' : e_ij}

第3，这个reduce_func函数以message_func函数来收集送出去的信息。之后收集节点数据Ah，然后由mailbox送出两个数据Bh_j和e_ij。而这条线h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)计算每一个节点的隐藏表示，方程式5显示出来。注意一点，但是是这样的，这个项$(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$是没有$\texttt{ReLU}(\cdot)$和残剩连接来表示出来的。

def reduce_func(self, nodes):
    Ah_i = nodes.data['Ah']
    Bh_j = nodes.mailbox['Bh_j']
    e = nodes.mailbox['e_ij']
    # sigma_ij = sigmoid(e_ij)
    sigma_ij = torch.sigmoid(e)
    # hi = Ahi + sum_j eta_ij * Bhj
    h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)
    return {'h' : h}

在forward函数中，叫g.update_all的话，我们就得到图形卷积的结果h和e，也就这一个项对应地表示出这个来自方程式5的项$(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$和来自方程式7的$\boldsymbol{e_{j}}$。之后我们就以「对着(respect)」图形的节点大小和图形边的大小，这个两个分别对应这两个h和e来归一化。而批量标准化就是之后用上的，所以我们就可以有效地训练网络。最后，我们用上一个$\texttt{ReLU}(\cdot)$和加一个残剩连接来为这些节点们和边们取得一些隐藏表示，也就之后以forward函数作为回传值回传出来。

def forward(self, g, h, e, snorm_n, snorm_e):

    h_in = h # 残剩连接
    e_in = e # 残剩连接

    g.ndata['h']  = h
    g.ndata['Ah'] = self.A(h)
    g.ndata['Bh'] = self.B(h)
    g.ndata['Dh'] = self.D(h)
    g.ndata['Eh'] = self.E(h)
    g.edata['e']  = e
    g.edata['Ce'] = self.C(e)

    g.update_all(self.message_func, self.reduce_func)

    h = g.ndata['h'] # 图形卷积的结果
    e = g.edata['e'] # 图形卷积的结果

    h = h * snorm_n # 以「对着(respect)」激活来归一化
    e = e * snorm_e # 以「对着(respect)」激活来归一化

    h = self.bn_node_h(h) # 批量标准化
    e = self.bn_node_e(e) # 批量标准化

    h = torch.relu(h) # 非线性激活
    e = torch.relu(e) # 非线性激活

    h = h_in + h # 残剩连接
    e = e_in + e # 残剩连接

    return h, e

下一步，我们定义MLP_Layer模组为一个包含多个完全性连接层(英文:fully connected layers (FCN))。我们创造一列连接层们，然后向前式通过这个网络。

最后我们定义我们的门控式图形卷积网络模型，英文代表为GatedGCN，也就包含之前定义好的类: GatedGCN_layer和MLP_layer。这个我们的模型的定义(GatedGCN)就在下方所示。

 class GatedGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, L):
        super().__init__()
        self.embedding_h = nn.Linear(input_dim, hidden_dim)
        self.embedding_e = nn.Linear(1, hidden_dim)
        self.GatedGCN_layers = nn.ModuleList([
            GatedGCN_layer(hidden_dim, hidden_dim) for _ in range(L)
        ])
        self.MLP_layer = MLP_layer(hidden_dim, output_dim)
    def forward(self, g, h, e, snorm_n, snorm_e):
        # 输入嵌入
        h = self.embedding_h(h)
        e = self.embedding_e(e)
        # 图形卷积层们
        for GGCN_layer in self.GatedGCN_layers:
            h, e = GGCN_layer(g, h, e, snorm_n, snorm_e)
        # MLP分类器
        g.ndata['h'] = h
        y = dgl.mean_nodes(g,'h')
        y = self.MLP_layer(y)
        return y

在我們的建構子，我們定義好用在e和h的嵌入(self.embedding_e和self.embedding_h)，而self.GatedGCN_layers也就是一列大小為$L$的，而且是我們之前定義好的模型: GatedGCN_layer，而且最後就是這個self.MLP_layer，也都是之前定義好的。下一步，用這些初始化的話，我們就簡單地向前式通過這個模型，然後就得出輸出y。

為了更好的明白模型，我們初始一個模型的物体，我們也把它顯示出來更好地用視覺來看清楚這個模型:

# 實例化這個網絡
model = GatedGCN(input_dim=1, hidden_dim=100, output_dim=8, L=2)
print(model)

實例化這個網絡

GatedGCN(
  (embedding_h): Linear(in_features=1, out_features=100, bias=True)
  (embedding_e): Linear(in_features=1, out_features=100, bias=True)
  (GatedGCN_layers): ModuleList(
    (0): GatedGCN_layer(...)
    (1): GatedGCN_layer(... ))
  (MLP_layer): MLP_layer(
    (FC_layers): ModuleList(...))

不出所料，我們有兩層來自GatedGCN_layer的層，那是我們在MLP_layer後設定了L=2，也就會輸出8個數值。

繼續說下去吧，我們定義出我們的train和evaluate函數。在我們的train函數，我們有我們的通用性的代碼，也就是由dataloader中取得一些樣本。下一步，batch_graphs和 batch_x﹑ batch_e﹑ batch_snorm_n ﹑ batch_snorm_e都被輸入到我們的模型中，也就是會回傳出batch_scores(大小為8)。而預測分數就會在損失函數中被用來與實際正確答案(ground truth)來做比較:loss(batch_scores, batch_labels)。之後，我們把梯度設回零(optimizer.zero_grad())，進行回傳(J.backward())和更新我們的權重(optimizer.step())。最後，每一個周期的損失和訓練準確度就會被計算出來了。加上，我們在evaluate函數中使用相似的代碼。

最後了，我們就準備好去訓練了!我們看到40個周期訓練，我們的模型就學到如何去分類出圖形，同時測試準確度為$87$%。