在能量基础模型中的对比法

回顾

杨立昆博士用了头15分钟来回顾能量基础模型。请看上星期(第七周笔记)的笔记来回顾一下，特别是对比学习法的概念。

就如上一次演讲中学到的，那里有两个主要学习方法的类型：

1. 对比法去推低训练数据点的能量 $F(x_i, y_i)$，同时推高其他地方的能量 $F(x_i, y’)$。
2. 建设法是写入会最小化或会限制低能量地区的能量函数$F$。

去区分不同的训练方法的特性，杨立昆博士进一步总结了前面提到的两类型训练的7种策略。其中一种是有点像最大似然法，也就是推低数据点的能量，同时推高其他地方的能量。

最大似然法概率地低推数个训练数据点的能量和同时推其他值为 $y’\neq y_i$的地方。最大似然不“在乎”能量的绝对值，但“在乎”能量的不同。因为概率分布是永远归一化，而加起来或积分都是1，比较两个给予的数据点之间比率是比简单地比较两个点的绝对值来说是更有用。

在自我监督学习中的对比法

在对比法中，我们推观察过的训练数据点，同时推高训练数据流型以外的点的能量。

在自我监督学习，我们使用一部份输入来预测另一部份。我们希望我们的模型能够生成能用在计算机视觉上的特征，而且可以媲美监督任务生成的特征。

研究人员已经凭经验学到把对比嵌入法用在自我监督学习模型中，其效能能够有好得可以与监督模型媲美。我们将在下面探讨这些方法及其结果。

Contrastive embedding

想一下这一对（$x$，$y$），$x$是图像，$y$是保留了$x$的内容和它的1变型(旋转，放大，裁剪等，和其他）。我们叫这个为正对。

图 1: 正对

从概念上讲，对比嵌入法是用一个卷积网络，然后送$x$和$y$到这个网络中来取得两个特征向量: $h$ 和 $h’$. Because $x$ 和 $y$ 有同样的内容（换句话说，一个正对），我们希望它们的特征向量尽可能相似。结果，我们选择一个相似测量(比如余弦相似度cosine similarity)和一个能最大化h和h’的相似度的损失函数。这样做的话，我们就能降低数据流型的能量。

图 2: 负对

另一面，我们也要推高数据流型以外的点的能量。所以我们也生成负样本 ($x_{\text{neg}}$, $y_{\text{neg}}$)，有不一样内容的图片(比如，不同类的标签)。在上方，我们送这些样本到我们的网路， 取得特征向量 $h$ 和 $h’$，和现在尝试去最小化它们之间的相似度。

这个方法容许我们去推低相似的配对的能量，同时推高不相似的配对的能量。

在ImageNet上最近的结果已经显示出这个方法能生成在物件识别上十分有用的特征，有用到可以媲美监督方法学出来的特征。

自我监督的结果（MoCo，PIRL，SimCLR）

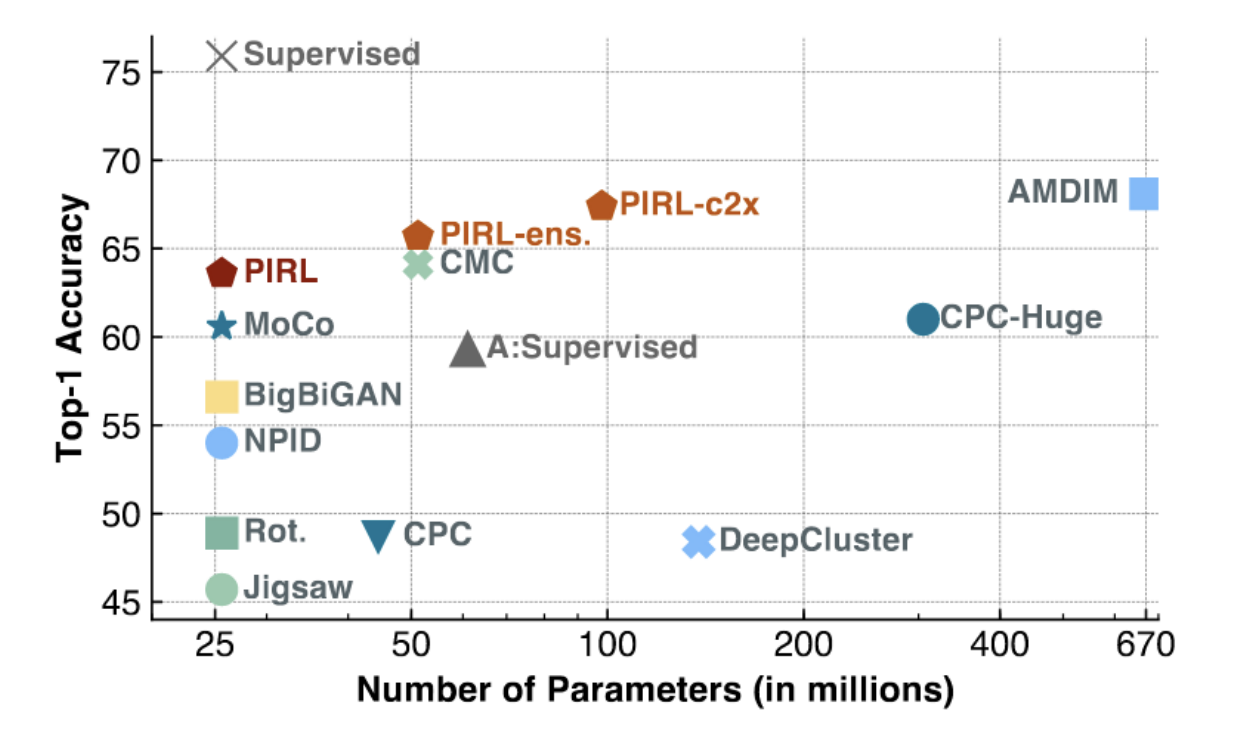
图 3: ImageNet上的PIRL和MoCo

如上图所示,MoCo和PERL取得SOTA成绩(特别是对于具有少量参数的低容量型号)。 PIR1开始接近监督基线的线性精度中的第一名（〜75％）。

我们可以看PIRL的目标函数来更了解它：噪声对比估计器(Noise Contrastive Estimator，英文简称NCE)如下。

在这里，我们将两个特征图/向量之间的相似度定义为余弦相似度(cosine similarity)。

而PIRL所做的不同是它没用直接用卷积特征提取器的输出。它反而定义不同的头， heads $f$ 和 $g$，它们可以被想像为一些在卷积特征提取器的底部上的独立层们。

把所有东西放在一起就看到，PIRL的噪声对比估计器NCE的目标函数就如接下来所说的那样运作，在一些「少批量」中(mini-batch或少量几个训练样本)，我们会有一个正对(相似的)的配对和很多负对(不相似的)的配对。我们之后就在「少批量」中计算转变后图片的特征向量($I^t$)和其他特征向量(一个正面，其余的负面)。我们之后在一个正配上以似Softmax函数( the score of a softmax-like function)计算出其分数。大化Softmax的分数就是说最小化其余的分数，也恰恰好好我们想要的能量基础模型。最后的损失函数，也就是，容许我们去建立一个模型去推低相似配对的能量，而同时去推高不相似的配对。

杨立昆博士提到要令这个运作，它要求大量的负样本。在SGD，这可能很难去一致地在「少批量」中维护大量的负相样本。所以，PIRL 也使用一个缓存的存储体。

问题:为什么我们要用余弦相似度而不是L2规范(L2 Norm)?答案:用L2规范的话，它会很容易去生成两个向量，这有点像令它们变短(靠近中心点)或令两个不相似的向量变得长(远离中心点)。这是因为L2规范是向量之间的局部差异的平方和(sum of squared partial differences between the vectors)。因此，使用余弦相似度强行令系统找出一个好解决方案而不是作弊的去令数个向量变短或变长。

SimCLR

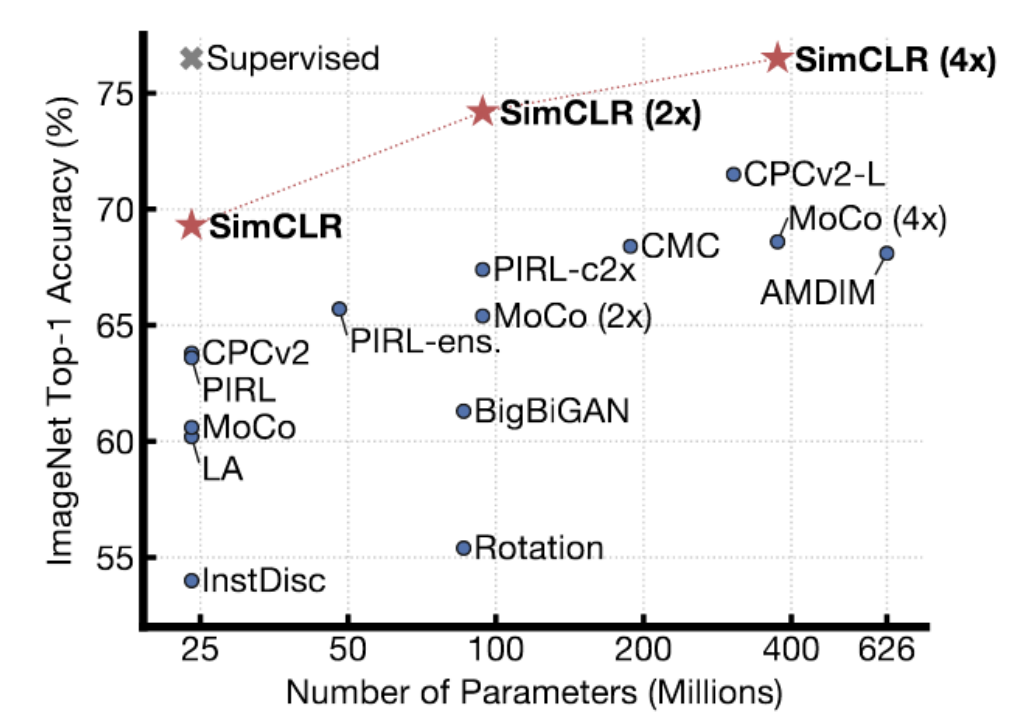
图 4: SimCLR Results on ImageNet

SimCLR显示出比之前方法有更好的结果。事实上，它到达了用了监督方法的ImageNet的效能，在ImageNet测试中有第一名的线性精度。这个技巧用了复杂的数据强化方法去生成相似的配对，和它们在TPUS上用了大量时间去训练(用了很…很大的批量大小)。杨立昆相信这个SimCLR，在一定程度上，显示出了对比法的极限。这里在高维度空间上有很…很多区域要你推高能量，去确保其能量是实质上比数据流形高。当你升高「表示」的维度时，你要更多负样本来确保能量是比那些不是在数据流形的地方更高。

降噪自动编码器

在 第七周的动手做中，我们讨论了降噪自动编码器。这个模型倾向于由损坏的输入重建回原本的输入来学习数据的「表示」。进一步来说，我们训练系统来生成能量函数，当损坏了的数据移开数据流形时，能量函数会数值二次地增长。

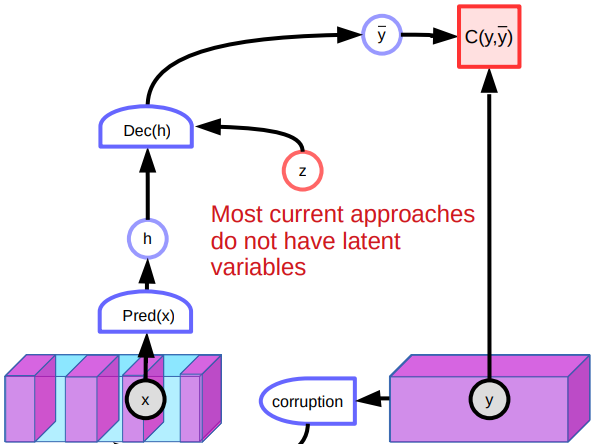
图 5: 降噪自动编码器的架构

问题

无论如何，降噪自动编码器的架构有数个问题。一个问题是它在高维度连续性空间中，那里有数之不尽的方法去损坏一部份数据，所以这里是没有通过简单地推高许多不同的位置，就能塑造能量函数的保证。另一个问题是模型是当没有足够的潜在变量时，其效能是不佳的。既然有那么多方法去重建图片，那系统生成各种预测和学不到特别的好特征。另外，在数据流形中的一些损坏点可以重建到流形中的两边。这会在能量函数中生成平点和影响整体效能。

其他的对比法

这里有其他对比法，比如对比散发(contrastive divergence)，比例匹配(Ratio Matching)，噪声对比估计( Noise Contrastive Estimation)和最小概率流(Minimum Probability Flow)。我们会简单的说下对比散发的基本概念。

对比散发(contrastive divergence)

对比散发是另一个模型由故意破坏输入样本来学习出「表示」。在连续的空间中，我们先选一个训练样本$y$和降低其能量。以这个样本，我们用一些基于梯度的处理来在噪声下在能量表面上向下移动。如果输入空间是离散的，相反，我们可以随机扰乱噪声训练样本来修改能量，如果我们得到的能量是更低，我们保持它。否则，我们在一些可能性下丢弃它。保持这样做会最终推低$y$的能量。我们可以由用损失函数来比例$y$和对比样本 $\bar y$ 来更新我们的能量函数的参数。

来更新我们的能量函数的参数。

其中一个对比散发的精美是持续性对比散发。系统会用一堆“颗粒”和记住它们的位置。这些粒子会在能量表面向下移动，就像我们过去对一般CD所做的一样。最终，它们会在能量表面找到低能量的地方，同时会令它们被推高。尽管如此，随着维数的增加，系统不会正确地扩展。