Çizge Evrişimsel Ağ

Çizge Evrişimsel Ağ’a (GCN) Giriş

Çizge Evrişimsel Ağ (GCN), veri yapısını kullanabilen mimarilerden bir tanesidir. Detaylarına değinmeden önce, öz-dikkat (self-attention) konusunu tekrar edelim çünkü GCN ve öz-dikkat konsept olarak birbirleriyle bağlı.

Tekrar: Öz-dikkat

• Öz-dikkat modülünde, elimizde bir girdi kümesi $\lbrace\boldsymbol{x}_{i}\rbrace^{t}_{i=1}$ ‘ne sahibiz. Dizinin aksine, küme sıralı değildir.
• Saklı vektör $\boldsymbol{h}$, kümedeki vektörlerin lineer kombinasyonuna eşittir.
• Saklı vektörü matris-vektör çarpımı $\boldsymbol{X}\boldsymbol{a}$ ile ifade edebiliriz. Burada $\boldsymbol{a}$ girdi vektörleri $\boldsymbol{x}_{i}$’ne ait katsayıları tutan vektördür.

Detaylı bir açıklama için, 12. haftanın notlarını gözden geçiriniz.

Notasyon

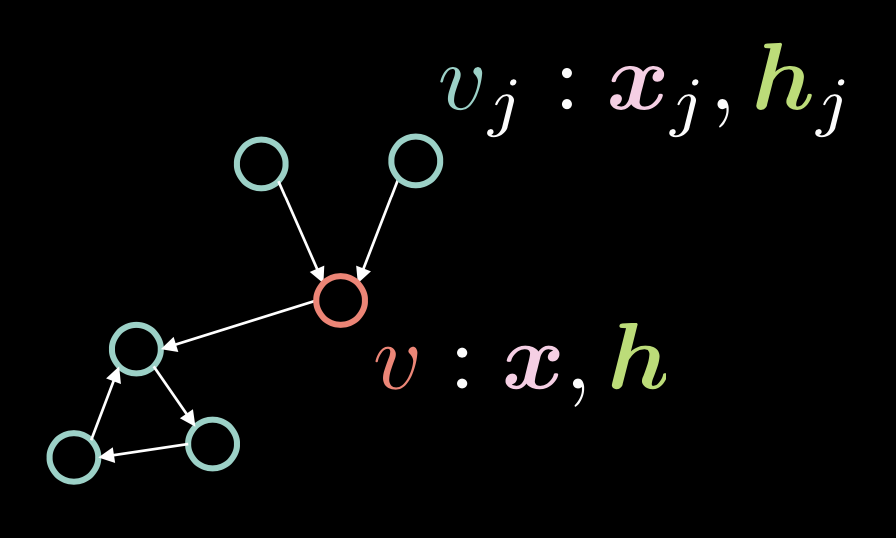
Şekil 1: Çizge Evrişimsel Ağ

Şekil 1’de, düğüm (vertex) $v$ iki vektörden oluşur: girdi $\boldsymbol{x}$ ve saklı gösterimi $\boldsymbol{h}$. Çizgemizde $v_{j}$, which is comprised of $\boldsymbol{x}_j$ and $\boldsymbol{h}_j$. Üstteki çizgede düğümler, yönlü ayrıtlar (directed edges) ile birbirlerine bağlıdır.

Yönlü ayrıtlar, komşuluk vektörü $\boldsymbol{a}$ ile ifade edilir, bu vektörün elemanı $\alpha_{j}$ eğer $v_{j}$’den $v$’ye gidilebiliyorsa 1 değerini alır.

Derece (degree) yani gelen ayrıtların sayısı $d$ komşuluk vektörünün normudur, $\Vert\boldsymbol{a}\Vert_{1} $, $\boldsymbol{a}$’daki 1’lerin sayısıdır.

Saklı vektör $\boldsymbol{h}$ aşağıdaki gibi gösterilir: \(\boldsymbol{h}=f(\boldsymbol{U}\boldsymbol{x} + \boldsymbol{V}\boldsymbol{X}\boldsymbol{a}d^{-1}) \tag{3}\)

burada $f(\cdot)$ doğrusal olmayan bir fonksiyondur (örn: ReLU $(\cdot)^{+}$, Sigmoid $\sigma(\cdot)$, ve hiperbolik tanjant $\tanh(\cdot)$.)

$\boldsymbol{U}\boldsymbol{x}$ terimi köşe $v$ ‘yi rotasyon operatörü $\boldsymbol{U}$’yu girdi $v$ üzerine uygulayarak dikkate alır.

Öz-dikkatte, saklı vektör $\boldsymbol{h}$ $\boldsymbol{X}\boldsymbol{a}$ ile hesaplanır, yani $\boldsymbol{X}$’teki sütunlar $\boldsymbol{a}$’daki skalerler ile ölçeklenir. GCN’leri düşündüğümüzde, eğer birsürü ayrıt geliyorsa, yani komşuluk vektörü $\boldsymbol{a}$’nın içinde bir sürü 1 var ise, $\boldsymbol{X}\boldsymbol{a}$ büyür. Diğer bir yandan, gelen sadece bir ayrıt var ise, bu değer küçülür. Bu ayrıtlar ile orantıdan oluşan sorunu çözmek için, değeri gelen ayrıtların sayısı $d$’ye böleriz. Sonra , $\boldsymbol{X}\boldsymbol{a}d^{-1}$’na $\boldsymbol{V}$ matrisi ile rotasyon uygularız.

Aşağıdaki matris notasyonu ile girdi kümesi $x$ için saklı gösterim $h$’ı ifade edebiliriz. \(\{\boldsymbol{x}_{i}\}^{t}_{i=1}\rightsquigarrow \boldsymbol{H}=f(\boldsymbol{UX}+ \boldsymbol{VXAD}^{-1}) \tag{4}\)

burada $\vect{D} = \text{diag}(d_{i})$ derece matrisi olarka da adlandırılır.

Artık Kapılı (Resıdual Gated) GCN Teorisi ve Kodlaması

Artık Kapılı Çizge Evrişimsel Ağ (Residual Gated Graph Convolutional Network) Şekil 2’deki gibi ifade edilebilen özel bir GCN’dir:

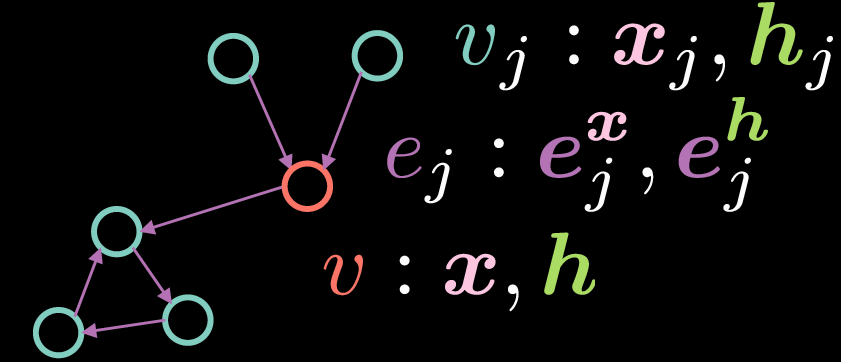
Şekil 2: Artık Kapılı Çizge Evrişimsel Ağ

GCN’lerde düğüm $v$, iki vektör ile ifade edilir: girdi $\boldsymbol{x}$ ve saklı gösterimi $\boldsymbol{h}$. Ancak bizim durumumuzda, ayrıtlar da iki vektör ile ifade edilmektedir: $\boldsymbol{e_{j}^{x}}$ kenar girdisini ifade ederken $\boldsymbol{e_{j}^{h}}$ ise ayrıtın saklı gösterimini ifade eder.

Düğüm $v$’nin saklı gösterimi $\boldsymbol{h}$ aşağıdaki gibi hesaplanır:

burada $\boldsymbol{x}$ girdiyi, $\boldsymbol{Ax}$ girdi $\boldsymbol{x}$’e uygulanan rotasyonu ve $\sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}}$ ise gelen öznitelikler $\boldsymbol{Bx_{j}}$ ile kapı $\eta(\boldsymbol{e_{j}})$’nin element çarpımlarının toplanmını ifade etmektedir. GCN’lerde gelen gösterimlerin ortalamasını alırken, Artık Kapılı GCN’deki kapının önemi büyüktür çünkü ayrıt gösterimlerine göre gelen gösterimleri modüle/kontrol etmemizi sağlar.

Dikkat ederseniz toplam sadece düğüm ${v}$’ye giren ayrıtlara sahip düğümler,${v_j}$ , üzerindedir. Ayrık (resıdual) terimi de saklı gösterim $\boldsymbol{h}$’ı hesaplarken girdi $\boldsymbol{x}$’i kullanmamızdan ötürü kullanılır. Kapı terimi $\eta(\boldsymbol{e_{j}})$ iaşağıdaki gibi hesaplanır:

Kapı değeri $\eta(\boldsymbol{e_{j}})$, gelen ayrıt gösteriminin sigmoidini tüm gelen ayrıt gösterimlerinin sigmoidleri toplamına bölünmesiyle normalize edilmiş bir sigmoiddir. Kapı teriminin hesabı için, ayrıt gösterimi $\boldsymbol{e_{j}}$’ne ihtiyaç duyulur ve aşağıdaki gibi hesaplanır:

Saklı ayrıt gösterimi $\boldsymbol{e_{j}^{h}}$ , ilk ayrıt gösterimi $\boldsymbol{e_{j}^{x}}$ ile $\texttt{ReLU}(\cdot)$ uygulanmış $\boldsymbol{e_{j}}$’nin toplamıdır. Burada $\boldsymbol{e_{j}}$, ayrı ayrı rotasyon uygulanmış $\boldsymbol{e_{j}^{x}}$ , düğüm $v_{j}$’nin girdi vektörü $\boldsymbol{x_{j}}$ ve düğüm 4v$’nin girdi vektörü $\boldsymbol{x}$ ‘nin toplamıdır.

Not: Üst katmanların saklı gösterimlerini hesaplamak için (örn. 2. katmanın saklı gösterimleri), girdi öznitelik gösterimlerini 1. katman öznitelik gösterimleriyle değiştirip yukarıdaki denklemi kullanabiliriz.

Çizge Sınıflandırması ve Artık Kapılı GCN Katmanı

Burada, çizge sınıflandırma (graph classification) sorununu tanıtacak ve Artık Kapılı GCN katmanı kodlayacağız. Kodlamadan önce, import komutlarımıza ilaveten aşağıdaki komutları da ekleyelim.

os.environ['DGLBACKEND'] = 'pytorch'
import dgl
from dgl import DGLGraph
from dgl.data import MiniGCDataset
import networkx as nx

İlk satır, DGL’e Pytorch backendini kullanmasını söyler. Deep Graph Library (DGL) çzgeler üzerinde değişik fonksiyonlar sunarken networkx ise çizgeleri görselleştirmemize yardımcı olur.

Bu notebookta amaç, verilen çizge yapısını 8 çizge türünden biri olarak sınıflandırmaktır. Veri kümesi, dgl.data.MiniGCDataset ile elde edilmiş olup istenen sayıda (num_graphs) ve belirli sayıda (min_num_v and max_num_v) düğümlere sahip çizgeler barındırmaktadır. Bu yüzden, elimizdeki çizgelerin hepsi aynı sayıda düğüme sahip değildir.

Not: DGLGraphs‘in temelleri için, bu tutorıal‘ı gözden geçirmenizi öneririm.

Çizgeleri oluşturduktan sonra yapılması gereken iş öznitelik eklemektir. Öznitelikleri DGLGraph‘ın düğüm ve ayrıtlarına ekleyebilmekteyiz. Öznitelikler, string ve tensörlerin oluşturduğu dictionary yapısıyla ifade edilir. ndata ve edataise tüm düğüm ve ayrıtların özniteliklerine ulaşmak için kullandığımız syntaxtir. Aşağıdaki kod parçası, özniteliklerin nasıl üretildiğini göstermektedir. Her bir düğüm kendisine gelen ayrıt sayısını tutarken ayrıtların tümüne 1 değeri atanmıştır.

def create_artificial_features(dataset):
    for (graph, _) in dataset:
        graph.ndata['feat'] = graph.in_degrees().view(-1, 1).float()
        graph.edata['feat'] = torch.ones(graph.number_of_edges(), 1)
    return dataset

Eğitim ve test veri kümeleri üretilier ve öznitelikler aşağıdaki gibi atanır:

trainset = MiniGCDataset(350, 10, 20)
testset = MiniGCDataset(100, 10, 20)

trainset = create_artificial_features(trainset)
testset = create_artificial_features(testset)

Eğitim kümesinden örnek bir çizge aağıdaki gösterime sahiptir. Çizgemiz 15 düğümden ve 45 ayrıttan oluşmakta ve beklendiği gibi düğüm ve ayrıt özniteliklerinin boyutları (1,)‘dir. Dahası, 0 sayısı çizgenin 1.inci sınıfa ait olduğunu gösterir.

(DGLGraph(num_nodes=15, num_edges=45,
         ndata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}
         edata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}), 0)

DGL Message ve reduce fonksiyonları Hakkında

DGL’de, message fonksiyonları (message functions) Edge UDF (User Defined Functions) yapıları ıle ifade edilir. Edge UDF’leri edges adında sadece bir tane argüman alırlar. Her bir edge, sırasıyla, başlangıç düğüm özelliklerine, bitiş düğüm özelliklerine ve ayrıt özelliklerine erişebilmeyi sağlayan src, dst, ve data adlı objeleri içinde barındırmaktadır. Bir diğer fonksiyonumuz reduce fonksiyonları (reduce functions) Node UDF yapılarıyla ifade edilir. Node UDF’ler, data ve mailbox objelerinden oluşan nodes argümanı ile ifade edilir. Burada data düğüm özelliklerini tutarken mailbox ise 2. boyutta yığılmış olan (yani dim=1 argümanı) tüm gelen mesaj özniteliklerini tutmaktadır. update_all(message_func, reduce_func) ise tüm ayrıtlardan mesajları gönderir ve tüm düğümleri günceller.

Artık Kapılı GCN Katmanı İmplementasyonu

Artık Kapılı GCN katmanı aşağıdaki kod parçalarında implement edilmiştir.

Önce, girdi öznitelikleri üzerinde gerçekleştirilen rotasyonlar $\boldsymbol{Ax}$, $\boldsymbol{Bx_{j}}$, $\boldsymbol{Ce_{j}^{x}}$, $\boldsymbol{Dx_{j}}$ ve $\boldsymbol{Ex}$, __init__ fonksiyonunda tanımlı nn.Linear katmanları yardımıyla tanımlanır ve girdi gösterimleri h ile e , forward fonksiyonunda tanımlı lineer katmanlarıyla ileri yayılır (forward propagation) .

class GatedGCN_layer(nn.Module):

    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.A = nn.Linear(input_dim, output_dim)
        self.B = nn.Linear(input_dim, output_dim)
        self.C = nn.Linear(input_dim, output_dim)
        self.D = nn.Linear(input_dim, output_dim)
        self.E = nn.Linear(input_dim, output_dim)
        self.bn_node_h = nn.BatchNorm1d(output_dim)
        self.bn_node_e = nn.BatchNorm1d(output_dim)

İkinci adımımızda, ayrıt gösterimlerini hesaplarız. Bu hesap, message_func fonksiyonunun tüm ayrıtlar üzerinde çalıştırarak ayrıt gösterimlerini hesaplamasıyla gerçekleştirilir. Özellikle e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh'] satırı, yukarıdaki (7.) denklemi ifade etmektedir. message_func fonksiyonu, Bh_j(5. denklemdeki $\boldsymbol{Bx_{j}}$ ) ve 7. denklemden e_ij‘yi ayrıt vasıtasıyla hedef düğümün posta kutusuna gönderir.

def message_func(self, edges):
    Bh_j = edges.src['Bh']
    # e_ij = Ce_ij + Dhi + Ehj
    e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']
    edges.data['e'] = e_ij
    return {'Bh_j' : Bh_j, 'e_ij' : e_ij}

Üçüncü adımımızda, reduce_func fonksiyonu message_func fonksiyonu ile iletilen mesajları toplar. Posta kutusundan düğüm verisi Ah , gönderilen veri Bh_j ve e_ij‘yi topladıktan sonra h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1) satırı, 5. denklemdeki gibi her bir düğümün saklı gösterimini hesaplar. Dikkat ederseniz bu terimde, $\texttt{ReLU}(\cdot)$ ve artık bağlantı (residual connection) uygulanmamıştır.

def reduce_func(self, nodes):
    Ah_i = nodes.data['Ah']
    Bh_j = nodes.mailbox['Bh_j']
    e = nodes.mailbox['e_ij']
    # sigma_ij = sigmoid(e_ij)
    sigma_ij = torch.sigmoid(e)
    # hi = Ahi + sum_j eta_ij * Bhj
    h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)
    return {'h' : h}

forward fonksiyonunda g.update_all çağırıldıktan sonra, 5. denklemde ifade edilen çizge evrişimi h ve e‘nin elde ederiz. h ve e sırasıyla 5. denklemdeki $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ ve 7. denklemdeki $\boldsymbol{e_{j}}$ ‘yi ifade etmektedir. Sonra, h and e ‘yi, sırasıyla, çizgedeki düğüm sayısı ve ayrıt sayısına göre normalize ederiz. Ağımızı etkili bir şekilde eğitebilmek için hemen sonrasında Batch normalization uygulanır. Sonunda, $\texttt{ReLU}(\cdot)$ uygular ve ayrık bağlantıyı ekleriz ki düğümler ve ayrıtlar için saklı gösterimleri forward fonksiyonu ile elde edebilelim.

def forward(self, g, h, e, snorm_n, snorm_e):

    h_in = h # residual connection
    e_in = e # residual connection

    g.ndata['h']  = h
    g.ndata['Ah'] = self.A(h)
    g.ndata['Bh'] = self.B(h)
    g.ndata['Dh'] = self.D(h)
    g.ndata['Eh'] = self.E(h)
    g.edata['e']  = e
    g.edata['Ce'] = self.C(e)

    g.update_all(self.message_func, self.reduce_func)

    h = g.ndata['h'] # result of graph convolution
    e = g.edata['e'] # result of graph convolution

    h = h * snorm_n # normalize activation w.r.t. graph node size
    e = e * snorm_e # normalize activation w.r.t. graph edge size

    h = self.bn_node_h(h) # batch normalization
    e = self.bn_node_e(e) # batch normalization

    h = torch.relu(h) # non-linear activation
    e = torch.relu(e) # non-linear activation

    h = h_in + h # residual connection
    e = e_in + e # residual connection

    return h, e

Daha sonra, içinde çeşitli tam bağlantılı katmanlar barındıran MLP_Layer modülünü tanımlıyoruz. Son olarak, GatedGCN_layer and MLP_layer sınıflarıyla GatedGCN modelini tanımlıyoruz. Modelimizin tanımı aşağıdaki gibidir.

 class GatedGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, L):
        super().__init__()
        self.embedding_h = nn.Linear(input_dim, hidden_dim)
        self.embedding_e = nn.Linear(1, hidden_dim)
        self.GatedGCN_layers = nn.ModuleList([
            GatedGCN_layer(hidden_dim, hidden_dim) for _ in range(L)
        ])
        self.MLP_layer = MLP_layer(hidden_dim, output_dim)
    def forward(self, g, h, e, snorm_n, snorm_e):
        # input embedding
        h = self.embedding_h(h)
        e = self.embedding_e(e)
        # graph convnet layers
        for GGCN_layer in self.GatedGCN_layers:
            h, e = GGCN_layer(g, h, e, snorm_n, snorm_e)
        # MLP classifier
        g.ndata['h'] = h
        y = dgl.mean_nodes(g,'h')
        y = self.MLP_layer(y)
        return y

Constructor’ımızda, e ve h için gömmelerimizi (embedding) (self.embedding_e and self.embedding_h), içinde GatedGCN_layer modellerini barındıran self.GatedGCN_layers adlı $L$ uzunluğunda bir list yapısı ve son olarak dha öncede tanımlanmış olan self.MLP_layer ‘ı tanımlıyoruz. Sonra, bu başlangıç değerlerini kullanarak, modelimiz üzerinden çıktı y‘yi elde ediyoruz.

Modeli daha iyi anlamak için, modelin objesini oluşturup yazdıralım:

# instantiate network
model = GatedGCN(input_dim=1, hidden_dim=100, output_dim=8, L=2)
print(model)

Modelimizin ana yapısı aşağıdaki gibidir:

GatedGCN(
  (embedding_h): Linear(in_features=1, out_features=100, bias=True)
  (embedding_e): Linear(in_features=1, out_features=100, bias=True)
  (GatedGCN_layers): ModuleList(
    (0): GatedGCN_layer(...)
    (1): GatedGCN_layer(... ))
  (MLP_layer): MLP_layer(
    (FC_layers): ModuleList(...))

Beklediğmiiz gibi, modelimizde iki adet GatedGCN_layer katmanı (çünkü L=2)) ve sonrasında 8 adet çıktı oluşturan bir MLP_layer katmanı bulunmaktadır.

Artık train ve evaluate fonksiyonlarımızı tanımlayabiliriz. İlk fonksiyonumuz train,dataloader objesinden örnekleri . Sonra, batch_graphs, batch_x, batch_e, batch_snorm_n ve batch_snorm_e modelimizin girdileri olarak kullanılır ve modelimiz bize anlık tahminlenen skorları ifade eden batch_scores (8 adet skor) adlı çıktıyı döndürür. Tahminlenen skorlar, kayıp fonksiyonunda gerçek değerler ile kıyaslanır: loss(batch_scores, batch_labels). Sonra, gradyenleri sıfırlıyor (optimizer.zero_grad()), geri yayılımı gerçekleştiriyor (J.backward()), ve ağırlıklarımızı güncelliyoruz (optimizer.step()). Son olarak, eğitim kümesindeki doğruluk oranını ve her epok için kaybı hesaplıyoruz. Ek olarak, yazdığımız kodu evaluate fonksiyonu için de kullanabiliriz.

Nihayet eğitime hazırız! 40 epok eğitim sonunda, modelimiz $87$% soğruluk payı ile çizgeleri sınıflandırmayı öğrenmiştir.