Enerjı Bazlı Modellerde Karşıtsal Yöntemler
Tekrar
Dr. LeCun dersin ilk 15 dakikasında enerji bazli modelleri tekrar etmişti. Bu konu icin lütfen bir önceki haftayı, özellikle karşıtsal öğrenme yöntemlerini, gözden geçiriniz.
Önceki dersten öğrendiğimiz üzere, öğrenme yöntemleri iki ana sınıfa ayrılmaktadır:
- Eğitim kümesindeki örneklerin enerjilerini $F(x_i, y_i)$ aşağı çekerken geri kalan her yerde ise enerjiyi yukarı iten $F(x_i, y’)$ Karşıtsal Yontemler.
- Düzenlileştirme yardımı ile sınırlı sayıda düşük enerji bölgelerine sahip bir enerji fonksiyonu F modelleyen Yapısal Yöntemler.
Farklı eğitim yöntemlerinin özelllklerini ayırt edebilmek için, Dr. Yann LeCun enerji fonksiyonunu biçimlendirmemizi sağlayan 7 strateji önermişti. Bu stratejilerden biri de veri noktalarının enerjisini aşağı çeken ve geri kalan tüm noktaların enerjisini iten En Büyük Olabilirlik (Maximum Likelihood) yöntemine benzer yöntemlerdir.
En Büyük Olabilirlik yöntemi olasılıksal bir şekilde eğitim kümesindeki verilerin enerjilerini aşağı çekerken geri kalan her yerde, ($y’\neq y_i$), enerjileri yukarı doğru iter. Bu yöntem enerjilerin “mutlak değerleri”nden ziyade “aralarındaki farkı” dikkate alır. Bunun sebebi ise olasılık dağılımlarının toplamının/integralinin her zaman 1 edecek şekilde normalize edilmesidir ki bu durumda herhangi iki noktanın oranına bakmak mutlak değerlerini kıyaslamaktan daha yararlıdır.
Özdenetimli öğrenmede Karşıtsal Yontemler
Karşıtsal yöntemlerde eğitim kümesinde gözlemiş olduğumuz örneklerin ($x_i$, $y_i$) enerjilerini aşağı iterken, eğitim kümesinin manifoldu dışında kalan örneklerin enerjlerini yukarı itiyoruz.
Özdenetimli öğrenmede girdinin bir kısmını kulllanarak diğer kısımlarını tahmin etmeye çalışırız. Bu öğrenme modelinden beklentimiz, modelimizin bilgisayarlı görü için denetimli görevlerle rekabet edebilecek seviyede iyi öznitelikler üretebilmesidir.
Araştırmacılar, özdenetimli öğrenme modellerinde karşıtsal gömülme (contrastive embedding) yöntemlerini uygulayarak denetimli modellere rakip olabilecek performanslar elde edilebildiğini deneysel olarak gözlemlemişlerdir. Bu yöntemlerden bazılarını ve sonuçlarını aşağıda inceleyeceğiz.
Karşıtsal Gömülme (Contrastive Embedding)
Bir çift ($x$, $y$) düşünelim, $x$’in bir görüntü ve $y$ de $x$ ‘in içeriği koruyan bir dönüşüm (döndürme, büyütme, kırpma, vb.) olsun. Bu çifti pozitif çift olarak adlandıralım.

Fig. 1: Pozitif Çift
Konsept olarak, karşıtsal gömülme yöntemleri, pozitif çifti evrişimsel bir ağın girdisi olarak kullanır ve iki öznitelik vektörü $h$ ve $h’$’ı öğrenir. Pozitif çift $x$ ve $y$ aynı içeriğe sahip olduğu için, öznitelik vektörlerinin de olabildiğince benzer olmalarını istiyoruz. Bu amacı gerçekleştirmek için, benzerlik metriği (kosinüs benzerliği gibi) ve $h$ ile $h’$ arasındaki benzerliği maksimize eden bir kayıp fonksiyonu tanımlamamız gerekiyor. Bunu yaparak, eğitim verisini barındıran manifoldun içinde bulunan tüm görüntülerin enerjilerini düşürüyoruz.

Fig. 2: Negatif Çift
Ancak, manifoldun dışında kalan noktaların enerjisini yukarı itmek zorundayız. Bu yüzden negatif örnekler, yani farklı içeriğe sahip resimler (örneğin farklı sınıf etiketi), ($x_{\text{neg}}$, $y_{\text{neg}}$), üretiyoruz. Bu örnekleri ağımıza girdi olarak verip, öznitelik vektörleri $h$ ile $h’$’ı elde ediyor ve bu iki vektör arasındaki benzerliği minimize etmeye çalışıyoruz.
Bu yöntem, benzer çiftlerin enerjisini aşağı çekerken benzer olmayan çiftlerin enerjilerini de yukarı itmemizi sağlar.
ImageNet’teki yeni sonuçlar bize bu yöntemin, nesne tanıma için denetimli öğrenme yöntemleriyle öğrenilen özelliklere rakip olabilecek derecede iyi özellikler üretebileceğini göstermiştir.
Özdenetimli Öğrenilmiş Sonuçlar (MoCo, PIRL, SimCLR)
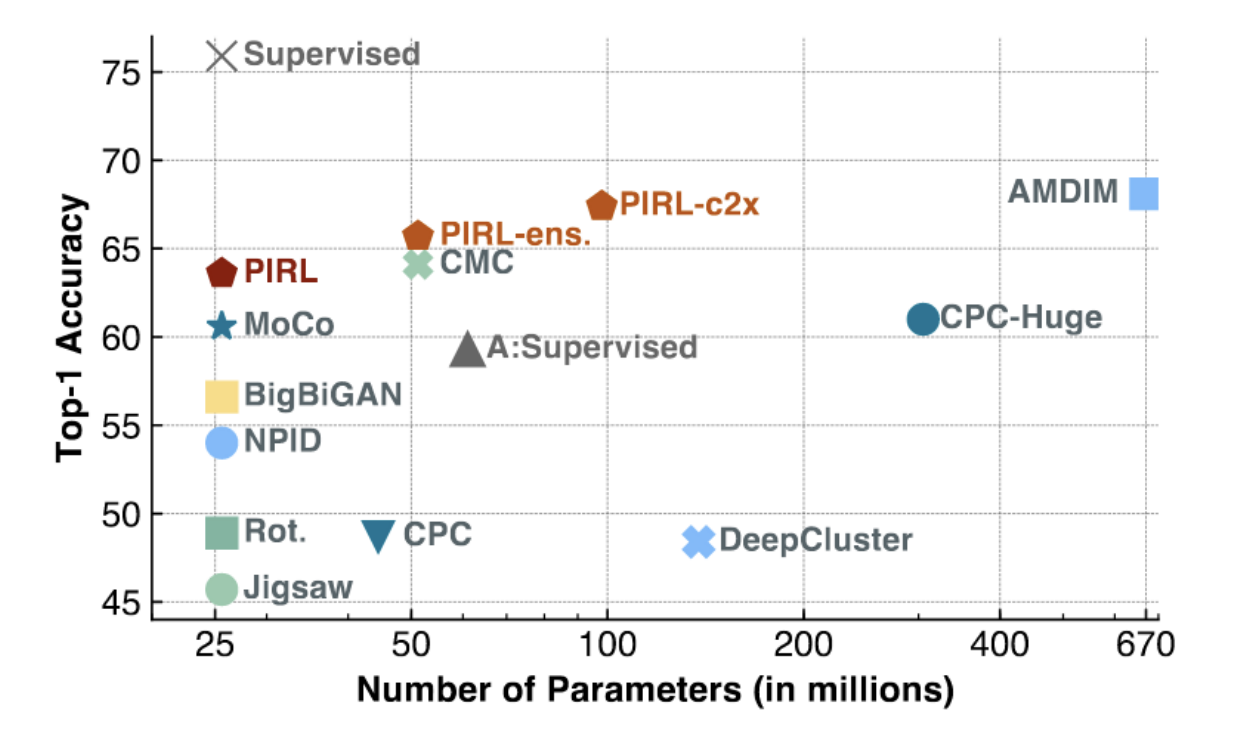
Fig. 3: ImageNet üzerinde PIRL ve MoCo
Yukarıdaki şekilde de görüldüğü üzere, MoCo ve PIRL SOTA (Alanının En İyisi, State of the Art) sonuçlara ulaşmıştır (özellikle az sayıda parametreli ve düşük kapasiteli modellerde). PIRl, diğer denetimli sistemlerin doğruluğuna (~75%) yaklaşmaya başlamıştır.
PIRL yöntemini, amaç fonksiyonu aşağıdaki gibi olan NCE’yi (Gürültüye Karşıt Kestirici, Noise Contrastive Estimator) inceleyerek daha iyi anlayabiliriz.
\[h(v_I,v_{I^t})=\frac{\exp\big[\frac{1}{\tau}s(v_I,v_{I^t})\big]}{\exp\big[\frac{1}{\tau}s(v_I,v_{I^t})\big]+\sum_{I'\in D_{N}}\exp\big[\frac{1}{\tau}s(v_{I^t},v_{I'})\big]}\] \[L_{\text{NCE}}(I,I^t)=-\log\Big[h\Big(f(v_I),g(v_{I^t})\Big)\Big]-\sum_{I'\in D_N}\log\Big[1-h\Big(g(v_{I^t}),f(v_{I'})\Big)\Big]\]Burada, iki özniitelik haritası/vektörü arasındaki benzerlik metriği kosinüs benzerliği olarak tanımlanmıştır.
PIRL’in farkı evrişimsel öznitelik üreticisinin çıktısını doğrudan kullanmamasıdır. Aksine, evrişimsel öznitelik üreticisinden bağımsız katmanlar, $f$ ve $g$, kullanır.
Her şeyi bir araya getirirsek, PIRL’in NCE amaç fonksiyonu şu şekilde çalışır. Bir miniyığında (mini-batch), bir pozitif (benzer) çift ve çok sayıda negatif (benzer olmayan) çiftlere sahip olalım. Önce, dönüştürülmüş resmin öznitelik vektörü ile miniyığındaki tüm örneklerin arasındaki benzerliği hesaplayalım. Sonra, pozitif çift için softmax-vari fonksiyonun skorunu hesaplayalım. Softmax skorunu maksimize etmemiz geri kalan tüm skorları minimize etmek demektir ki bu bizim enerji bazlı modellerde istediğimiz bir durumdur. Böylelikle, NCE kayıp fonksiyonu, benzer çiftlerin enerjilerini aşağı iterken benzer olmayan çiftlerin enerjilerini de yukarı itmemize olanak veren bir model tasarlamamızı sağlar.
Dr. LeCun, PIRL’ın çalışması için oldukça fazla sayıda negatif örneğe ihtiyaç uyulduğunu belirtmektedir. SGD’de miniyığındaki negatif örneklerin çoğunu sürekli olarak tutabilmek zor olabilir. Bü durumu çözmek için PIRL, özel bir ön bellek yapısı kullanmaktadır.
Soru: L2 normu yerine neden kosinüs benzerliği kullanıyoruz? Cevap: Çünkü, oldukça kısa (merkeze yakın) ya da oldukça uzun (merkezden uzak) iki vektör seçersek bu iki vektör L2 normuna göre birbirlerine benzer diyebiliriz. Bunun sebebi, L2 normunun vektörlerin elemanları arasındaki farklarının kareleri toplamıdır. Dolayısıyla, kosinüs benzerliği kullanarak sistemimizi “hile yapmamaya” yani vektörleri uzaltıp kısaltmadan iyi bir sonuç bulmaya zorluyoruz.
SimCLR
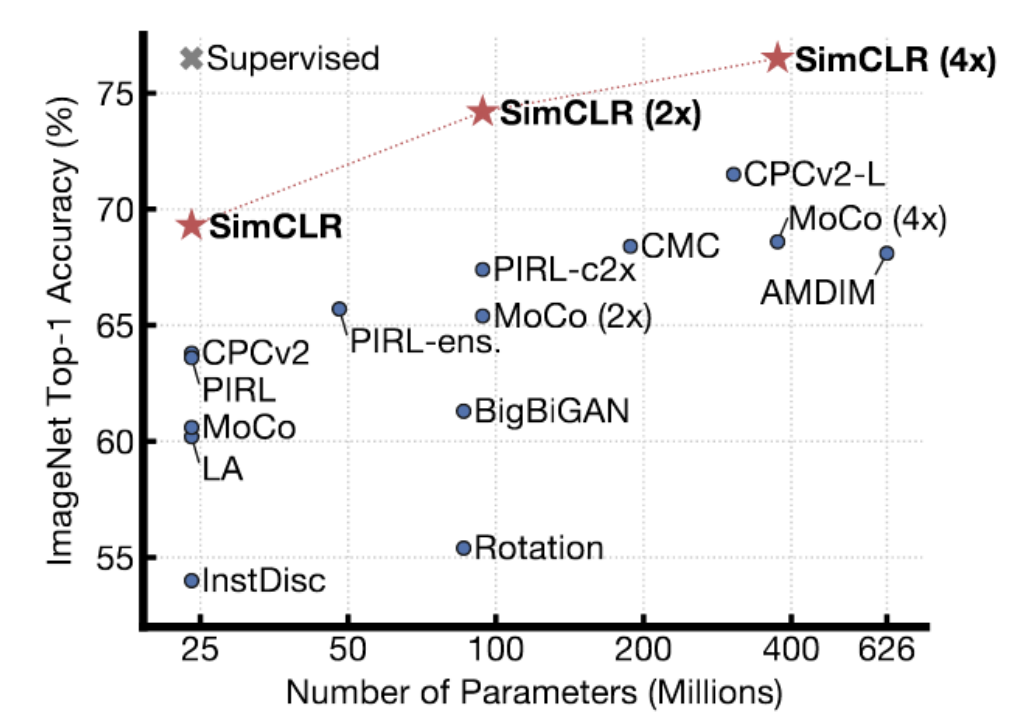
Fig. 4: SimCLR'ın ImageNet Üzerindeki Sonuçları
SimCLR önceki metodlardan daha iyi sonuçlar göstermektedir. Hatta, denetimli metodlarin Imagenet’te ulaştığı en iyi 1. lineer doğruluk performansına erişmiştir. benzer çiftler oluşturmak için karmaşık bir veri büyütme yöntemi kullanır ve TPU’larda büyük miktarda (çok, çok büyük parti yığınlarla) eğitim yapar. Dr. LeCun, SimCLR’in bir ölçüde karşıtsal yöntemlerin sınır çizgisi olduğuna inanmakta. Yüksek boyutlu bir uzayda, veri manifoldundan gerçekten daha yüksek olduğundan emin olmak için enerjiyi yükseltmeniz gereken birçok bölge var. Gösterimlerin boyutları arttıkça, daha fazla negatif örneğe ihtiyaç duyulmaktadir ki enerjinin manifold üzerinde olmayan bölgelerinde daha yüksek olması şartı sağlanabilsin.
Arıtan Otokodlayıcılar
7. haftanın uygulamasında, arıtan otokodlayıcıdan bahsetmiştik. Bu yapı, veri gösterimini bozuk girdiyi orjinal veriye geri dönüştürmeye çalışarak öğrenir. Detaylıca bahsedersek, sistemi, bozulmuş veriler veri manifoldundan uzaklaştıkça karesel bir oranda büyüyen bir enerji fonksiyonu üretebilmesi için eğitiyoruz.
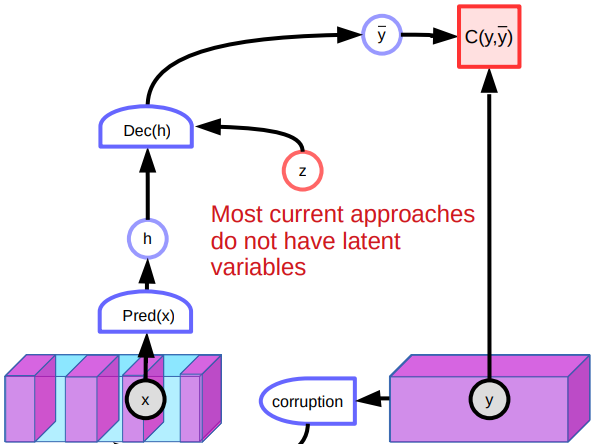
Fig. 5:Arıtan Otokodlayıcı Mimarisi
Problemler
Ancak arıtan otokodlayıcılar ile ilgili çeşitli sorunlar bulunmaktadır. Öncelikle, çok boyutlu ve sürekli bir uzayda, veriyi bozmanın sonsuz sayıda yolu vardır. Bu yüzden enerji fonksiyonunu basitçe bir sürü değişik bölgede yukarı iterek şekillendirebileceğimizin garantisi yoktur. Bir diğer problem ise saklı değişkenlerin noksanlığından ötürü arıtan otokodlayıcılar görüntülerde kötu performans sergilemektedir. Bir resmi yeniden oluşturmanın sayısız yöntemi olduğundan, sistem çeşitli tahminler üretir ve bilhassa iyi öznitelikler öğrenemez. Ayrıca, manifoldun ortasında kalan bozunmuş noktaları iki taraftan da onarmamız mümkün. Bu durum enerji fonksiyonumuzda düz bölgeler oluşmasına neden olur ve genel performansı etkiler.
Diger Karşıtsal Yontemler
Karşıtsal ıraksama (Contrastive divergence), Oran Eşleştirme (Ratio Matching), Gürültüye Karşıt Kestirim (Noise Contrastive Estimation) ve Minimum Olasılık Akışı (Minimum Probability Flow) gibi çeşitli karşıtsal yöntemler literatürde bulunmaktadır. Bu bölümde, karşıtsal ıraksamanın arkasında yatan temel fikirden bahsedeceğiz.
Karşıtsal Iraksama(Contrastive Divergence)
Karşıtsal Iraksama (CD) girdileri akıllıca bozarak veri gösterimi öğrenmeyi hedefler. Sürekli bir uzayda, önce eğitim kümemizden bir örnek $y$ seçip sonra onun enerjisini düşürüyoruz. Seçtiğimiz örnek için, gradyan bazlı bir süreç ile gürültü kullanarak enerji yüzeyinde hareket ediyoruz. Eğer girdilerimiz ayrık bir uzaydan alınıyorsa, örneği rastgele bozmamız o örneğin enerjisini değiştirmek için yeterli olacaktır. Bozunum sonucu eğer enerji düşüyor ise o örneği tutuyoruz. Aksi takdirde, belli bir olasılık ile o örneği atıyoruz. Bu süreci devam ettirdikçe $y$’nin enerjisi de en sonunda düşecektir. Daha sonra, enerji fonksiyonumuzun parametresini $y$ ve zıtlaştırılmış örneğimiz $\bar y$’i kayıp fonksiyonu kullanarak kıyaslayıp güncelleyebilmiş oluruz.
Kalıcı Karşıtsal Iraksama (Persistent Contrastive Divergence)
Karşıtsal Iraksama’nın özel bir versiyonu ise Kalıcı Karşıtsal Iraksama yöntemidir. Önceki yönteme kıyasla sistem, konumunu hatırlayabilen bir grup “parçacık” kullanır. Bu parçacıklar tıpkı CD’deki gibi enerji yüzeyinde hareket ettirilir. Sonunda, bu parçaçıklar enerji yüzeyimizdeki düşük enerjili yerleri bulacak ve yukarı itilmelerini sağlayacaktır. Ancak, boyut arttıkça sistem performansı kötü etkilenmektedir.
📝 Vishwaesh Rajiv, Wenjun Qu, Xulai Jiang, Shuya Zhao
emirceyani
23 Mar 2020