畳み込みと自動微分エンジンを理解する

1次元畳み込みを理解する

データのスパース性、定常性、構成性を議論したいので、このパートでは、畳み込みについて説明します。

前の週 で説明した行列$A$を使用する代わりに、行列の幅をカーネルサイズ$k$に変更します。 したがって、行列の各行はカーネルです。 スタックやシフトでカーネルを使用できます（図1を参照）。 すると、高さ$n-k + 1$の層を$m$層を作成できます。

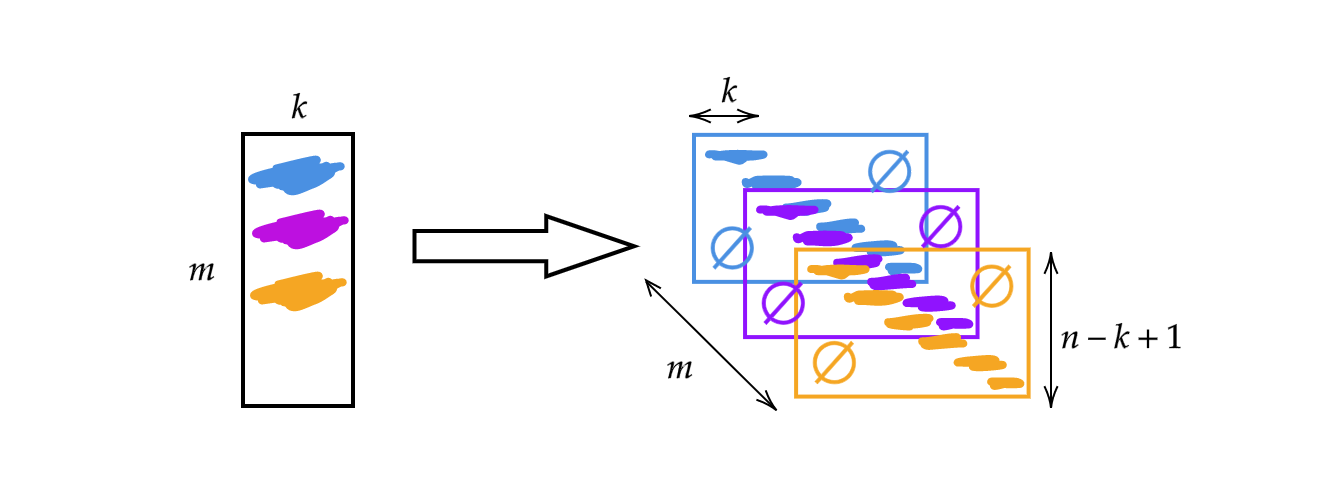
図1: １次元畳み込みの例

出力は、サイズ$n-k + 1$の厚さ$m$のベクトルです。

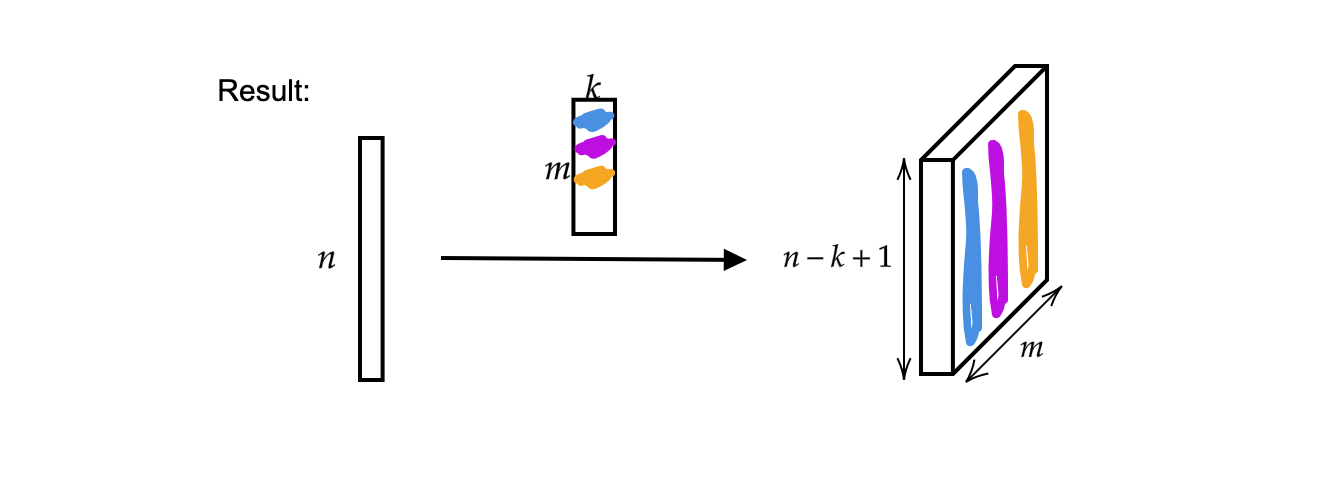
図2: １次元畳み込みの結果

さらに、単一の入力ベクトルは単旋律の信号と見なすことができます。

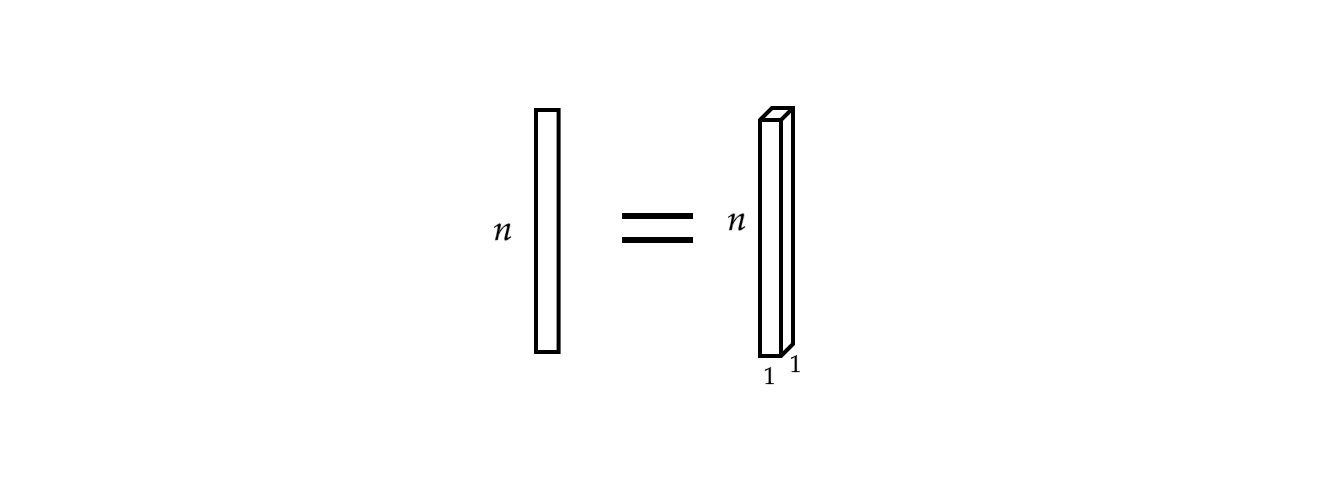
図3: 単旋律の信号

今、入力$x$は写像です

ここで、$\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb {N}^1$（これは$1$次元の信号です。なぜなら$1$次元のドメインがあるからです。）で、この場合はチャネル数$c$は$1$です。$c = 2$の場合、これはステレオ（複旋律）信号になります。

１次元畳み込みの場合、カーネルごとにスカラー積で計算します（図4を参照）。

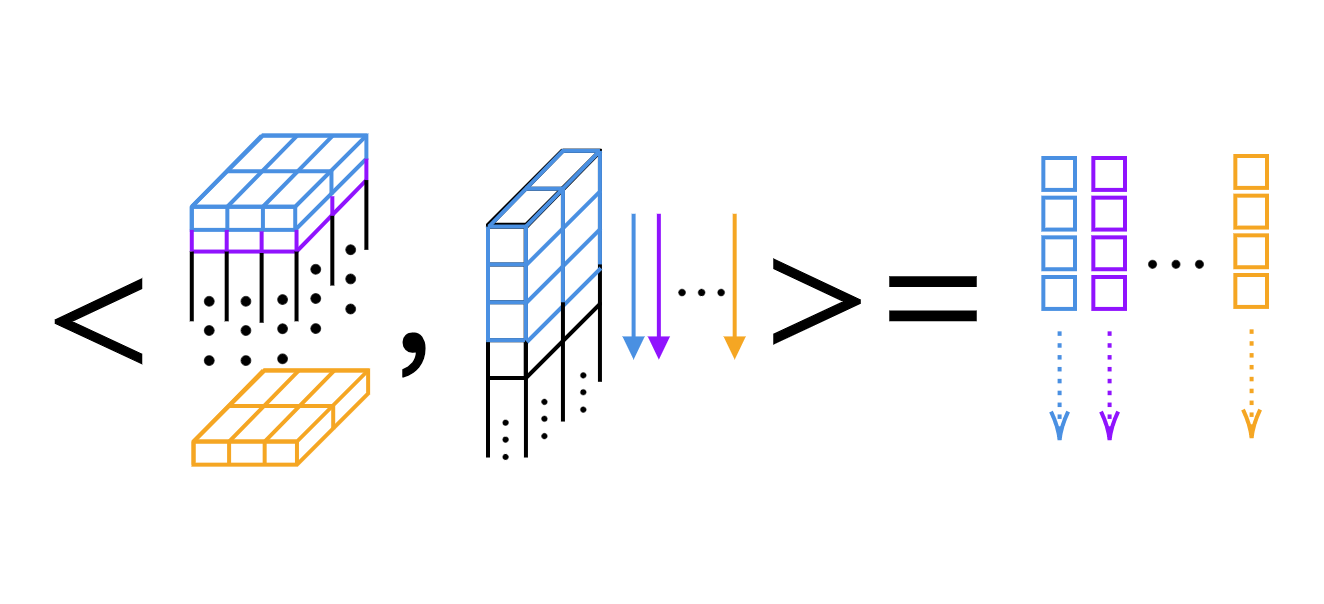
図4: 層ごとにスカラー積での畳み込み

PyTorchにおけるカーネルと出力幅の次元

ヒント：IPythonでは ？ を使用して、関数のドキュメントにアクセスできます。 例えば、

Init signature:
nn.Conv1d(
	in_channels,           # number of channels in the input image
	out_channels,          # number of channels produced by the convolution
	kernel_size,           # size of the convolving kernel
	stride=1,              # stride of the convolution
	padding=0,             # zero-padding added to both sides of the input
	dilation=1,            # spacing between kernel elements
	groups=1,              # nb of blocked connections from input to output
	bias=True,             # if `True`, adds a learnable bias to the output
	padding_mode='zeros',  # accepted values `zeros` and `circular`
)

1次元畳み込み

カーネルサイズは$3$、ストライドは$1$で、$1$次元の畳み込みを$2$チャネル（ステレオ信号）から$16$チャネル（$16$カーネル）へ変換します。次は、厚さが$2$、長さが$3$の$16$カーネルが続きます。仮に入力信号のバッチサイズが$1$（1つの信号）であり、チャネル数は$2$、サンプル数は$64$とすると、出力層の信号数は$1$、チャネル数は$16$、信号の長さは$62$（$= 64-3 + 1$）となります。また、バイアスのサイズも出力すると、重みごとに1つのバイアスがあるため、バイアスのサイズは$16$であることがわかります。

conv = nn.Conv1d(2, 16, 3)  # 2 channels (stereo signal), 16 kernels of size 3
conv.weight.size()          # output: torch.Size([16, 2, 3])
conv.bias.size()            # output: torch.Size([16])

x = torch.rand(1, 2, 64)    # batch of size 1, 2 channels, 64 samples
conv(x).size()              # output: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2 channels, 16 kernels of size 5
conv(x).size()              # output: torch.Size([1, 16, 60])

2次元畳み込み

入力データを、高さ$64$、幅$128$の$1$サンプル、$20$チャネル（たとえば、ハイパースペクトル画像を使用）だとします。2次元畳み込みは、入力からの$20$チャネルと、サイズが$3 \times 5$の$16$カーネルです。 畳み込み後、出力データには$1$サンプル、高さ$62$（$= 64-3 + 1$）、幅$124$（$= 128-5 + 1$）の$16$チャネルがあります。

x = torch.rand(1, 20, 64, 128)    # 1 sample, 20 channels, height 64, and width 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 channels, 16 kernels, kernel size is 3 x 5
conv.weight.size()                # output: torch.Size([16, 20, 3, 5])
conv(x).size()                    # output: torch.Size([1, 16, 62, 124])

次元数が維持したい場合は、パディングを使用することができます。上記により、畳み込み関数に新しいパラメーター stride = 1と padding =（1、2） を追加できます。これは、$y$方向に$1$（上部に$1$、底部に$1$）と$x$方向に$2$を意味します。 その場合、出力信号のサイズは入力信号のサイズと同じです。 2次元畳み込みを実行するときにカーネルの関数を保存するために必要な次元の数は$4$です。

# 20 channels, 16 kernels of size 3 x 5, stride is 1, padding of 1 and 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # output: torch.Size([1, 16, 64, 128])

自動微分の仕組み

このセクションでは、偏微分を計算するように、PyTorchのテンソルにすべての計算をチェックするように依頼します。

• 勾配を蓄積する機能を備えた$2 \times2$テンソル$\boldsymbol {x}$を作成します。
• $\boldsymbol {x}$のすべての座標値から$2$を差し引き、$\boldsymbol {y}$を取ります。 （ y.grad_fnを出力すると、 <SubBackward0 object at 0x12904b290> が得られます。つまり、 yは減算$\boldsymbol {x} -2$のモジュールによって生成されます。また、y.grad_fn.next_functions [0] [0] .variableを使用して、元のテンソルを導出することもできます。）
• 次の操作は：$\boldsymbol {z} = 3 \boldsymbol {y} ^ 2$;
• $\boldsymbol {z}$の平均を計算します。

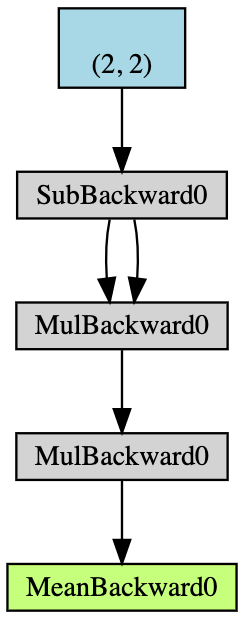
図5: 自動微分の例のフローチャート

バックプロパゲーションは、勾配の計算に使用されます。 この例では、バックプロパゲーションのプロセスは、勾配$\frac {d \boldsymbol {a}} {d \boldsymbol {x}}$を計算するものと見ることができるでしょう。検証として$\frac {d \boldsymbol {a}} {d \boldsymbol {x}}$を手動で計算したすると、a.backward（）で計算したx.gradの値は、私たちの手動による計算の結果と同じだとわかります。

手動でバックプロパゲーションを計算するプロセスは次のとおりです。

PyTorchで偏微分を使用する場合、常に元のデータと同じ次元数が得られます。 しかし、正しいヤコビ行列は転置されたものになります。

基本的なものから変わったものへ

これで、$1 \times3$ベクトル$x$を手に入れ、$y$をダブル$x$に割り当て、ノルムが$1000$より小さくなるまで$y$を2倍し続けます。 $x$にはランダム性があるため、反復数計算はいつ終わるかは簡単にはわかりません。

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

ただし、勾配の値で推測できます。

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

推測に関しては、以下に示すように、 requires_grad = Trueを使用して、勾配の蓄積を追跡したいというラベルをつけます。$x$または$w$の宣言で requires_grad = Trueを省略し、$z$で backward（） を呼び出すと、$x$と$w$の勾配がいっさい積算されてないため、ランタイムエラーが発生します。

# Both x and w that allows gradient accumulation
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

また、with torch.no_grad()で勾配の蓄積が省略できます。

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# All torch tensors will not have gradient accumulation
with torch.no_grad():
    z = w @ x

try:
    z.backward()  # PyTorch will throw an error here, since z has no grad accum.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

その他：勾配値をカスタマイズする

また、基本的な数値計算の代わりに、ニューラルグラフに導入できる自己定義モジュール/関数を生成 することができます。 Jupyter Notebookはここにあります。

そのためには、 torch.autograd.Functionのクラスを継承し、 forward（） 関数と backward（） 関数を上書きする必要があります。 たとえば、ネットワークを訓練する場合は、フォワードパスを取得し、出力に関する入力の偏微分を知ることで、コード内の任意の箇所でこの新モジュールが使用できるようにする必要があります。 すると、出力に対する入力の偏微分がわかっている限り、バックプロパゲーション（チェーンルール）を使って、連鎖した演算の任意のところにも何かしら導入することができます。

この場合、ノートブックにはカスタムモジュールの3つの例、「add」、「split」、および「max」モジュールがあります。 たとえば、カスタム加算モジュールは次のとおりです。

# Custom addition module
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx is a context where we can save
        # computations for backward.
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # need to return grads in order
        # of inputs to forward (excluding ctx)
        return grad_x1, grad_x2

2つの和を計算して出力を取得する場合は、このようにフォーワードパス関数を上書きする必要があります。 そして、バックプロパゲーションを行うために計算グラフを降っていくと、勾配が両側にコピーされます。 そのため、バックワード関数をコピーして上書きします。

splitと maxについては、ノートブックのフォーワードパス関数とバックワードパス関数を上書きする方法のコードを参照してください。 Splitと同じものから来た場合、勾配をコピーしてから加算/合計する必要があります。 argmaxの場合、最も高い値に属したインデックスは$1$で、他のインデックスは$0$のように、最も高い値に対応するインデックスを選択します。さまざまなカスタムモジュールに応じて、各自のフォワードパスと、バックワード関数での勾配の実行方法を上書きする必要があることを忘れないでください。