線形代数と畳み込み

🎙️ Alfredo Canziani

線形代数の復習

このパートでは、ニューラルネットワークの文脈における基本的な線形代数についておさらいします。 まずは単純な隠れ層$\boldsymbol{h}$から始めます:

\[\boldsymbol{h} = f(\boldsymbol{z})\]

この出力は　ベクトル$z$　に非線形関数　$f$　が適用された結果です。 ここの $z$ は　入力されたベクトル　$\boldsymbol{x} \in\mathbb{R^n}$　を$\boldsymbol{A} \in\mathbb{R^{m\times n}}$によってアフィン変換した結果です:

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

簡単にするために、バイアスを無視します。上記の線形方程式は次のように展開できます。

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

上記の $\boldsymbol{a}^{(i)}$ は行列 $\boldsymbol{A}$　のなかの第$i$行です。

この変換の意味を理解するために、$a^{(1)}\boldsymbol{x}$などの $\boldsymbol{z}$の1つの要素を分析してみましょう。例えば $n=2$とすると、$\boldsymbol{a} = (a_1,a_2)$　および　$\boldsymbol{x} = (x_1,x_2)$となります。

$\boldsymbol{a}$および$\boldsymbol{x}$は、2次元座標系上のベクトルとして描画できます。 ここで、$\boldsymbol{a}$と$\hat{\boldsymbol{\imath}}$の間の角度が$\alpha$で、$\boldsymbol{x}$と$\hat{\boldsymbol{\imath}}$の間の角度が、$\xi$であるとします。すると、三角関数の公式を用いることで、$a^\top\boldsymbol{x}$は次のように展開できます。

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

この出力は入力されたベクトルが行列$\boldsymbol{A}$の特定の行とどのぐらい同じ方向を向いているかを測る値です。 これは、2つのベクトルの間の角度　$\xi-\alpha$を観察することで、理解することができます。 $\xi = \alpha$である場合、2つのベクトルは完全に同じ方向を向いており、最大値となります。 もし　$\xi - \alpha = \pi$である場合、2つのベクトルはお互いに反対方向を指すため　$\boldsymbol{a}^\top\boldsymbol{x}$ 最小値となります。 要するに、この線形変換により、入力されたベクトルが$ A $で定義されたさまざまな方向へ射影された値を見ることができます。 このようなやりかたは、より高い次元にも適用することができます。

線形変換を理解するもう1つの方法は、$ \ boldsymbol {z} $も次のように展開すれば：

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

出力は、行列$\boldsymbol{A}$の列で重み付けられた和です。 よって、信号は入力を組み合わせたものにすぎません。

線形代数の概念を畳み込みへ展開

次に、音声データ分析の例を使用して、線形代数の概念を畳み込みに拡張します。 まずは、全結合層を行列積の形式で表すと：

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

この例では、重み行列のサイズは$4 \times 3$、入力ベクトルのサイズは$3 \times 1$なので、出力ベクトルのサイズは$4 \times 1$です。

ただし、音声データの場合、データサイズは非常に長くなります（サイズはもう3ではありません）。 音声データのサンプル数は、 音声の時間（例：3秒）$\times$サンプリングレート（例： 22.05 kHz） です。 下記のように、入力ベクトル$\boldsymbol{x}$は非常に長くなります。 よって、重み行列は「寸胴」になります。

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

このような式は学習が困難になります。 幸いなことに、同じことを単純にできる方法があります。

局所性

データの局所性（例：遠くにあるデータ点は対象外となる）により、 上記の重み行列の$w_{1k}$ は、$k$の値が大きい場合に0で埋めることができます。 よって、行列の最初の行のカーネルは3のサイズはになります。 このサイズ3のカーネルを$\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$としましょう。

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

定常性

自然信号には定常性があります（特定のパターン/モチーフが繰り返されます）。 ですので、先ほど定義したカーネル$\mathbf{a}^{(1)}$を再利用することができます。 毎回１ステップ飛ばし（例：ストライドが1）でこのカーネルを使用すると、下記のようになります：

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

局所性のおかげで、行列の右上部分と左下部分の両方も$0$ で埋めることができ、行列がスパースになります。 特定のカーネルを何度も再利用することは重み共有と呼ばれます。

多層テプリッツ行列

上記の特性を使って変更すると、残ったパラメーターの数は3つだけとなります（例： $a_1, a_2, a_3$）。 これを前回の12個のパラメーターの重み行列（例： $w_ {11}, w_ {12}, \cdots, w_{43}$）と比較すると、今のパラメーター数は制限され過ぎています。これを同じように展開したいと考えます。

前の行列は、カーネル$\boldsymbol{a}^{（1）}$付きのある層（例：畳み込み層）と見なすことができます。 次に、異なったカーネル$\boldsymbol{a}^{（2）}$や$\boldsymbol{a}^{（3）}$などで複数の層を作成し、パラメーター数を増やすことができます。

各層は、ただ一つの多数複製されたカーネルを含む行列を持ちます。このタイプの行列は、テプリッツ行列と呼ばれます。このようなのテプリッツ行列では、対角要素は一定とされます。ここで使用するテプリッツ行列は、スパース性もあります。

最初のカーネル$\boldsymbol{a}^{（1）}$と入力ベクトル$\boldsymbol {x}$が与えられると、この層で出力の最初の要素は$a_1^{（1）}x_1 + a_2 ^ {（1）} x_2 + a_3 ^ {（1）} x_3$となります。したがって、出力ベクトル全体は次のようになります。

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

異なるカーネルを持つ次の畳み込み層例： $\boldsymbol{a}^{（2）}$と$\boldsymbol{a}^{（3）}$）に対しても同じ行列積を適用することができ、同様の結果を得ることができます。

Listening to convolutions - Jupyter Notebook

Jupyter Notebookはここにあります.

このノートブックでは、「スカラー積」としての畳み込みのやりかたを理解していきます。

ライブラリ librosaを使用すると、オーディオクリップ$\boldsymbol {x}$とそのサンプリングレートを読み込むことができます。 この例では、サンプルは70641個あり、サンプリングレートは22.05kHz、クリップの全長は3.2秒です。読み込まれた音声信号はばらつきがあり（図1を参照）、$y$軸の振幅から見るとどのような声がするのかを推測することができます。音声信号$x(t)$は、実際にはWindowsシステムをオフにしたときに再生されるサウンドです（図2を参照）。

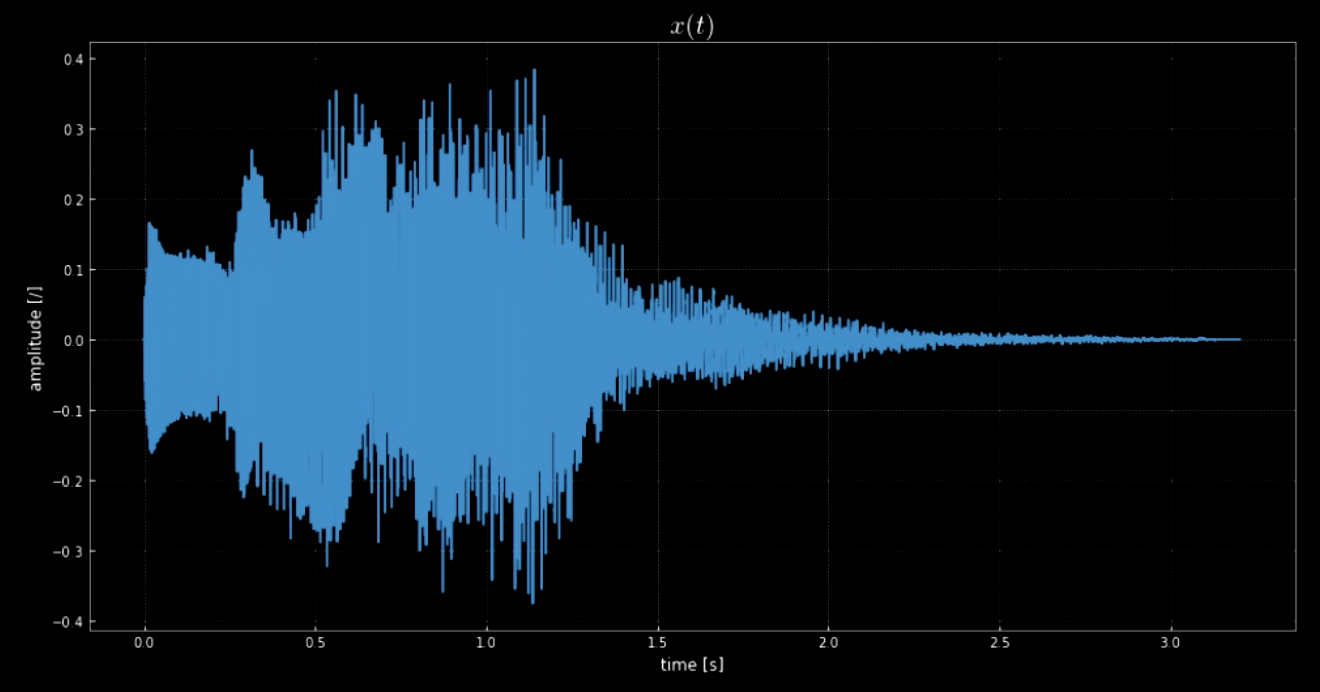
図1: 音声信号の可視化

図2: 上の音声信号に対する注意

波形から音符を分離する必要があります。 これをフーリエ変換（FT）で行おうとすると、すべての音が一緒に出て、各ピッチの正確な時間と場所を把握するのが難しくなります。よって、局所化されたFTが必要となります（スペクトログラムとも呼ばれます）。スペクトログラムをみるとわかるように（図3を参照）、異なったピッチと異なった周波数でピークが見えます（例： 1600で最初のピッチピーク）。 それらの周波数で4つのピッチを連結すると、元の信号がピッチされたものが得られます。

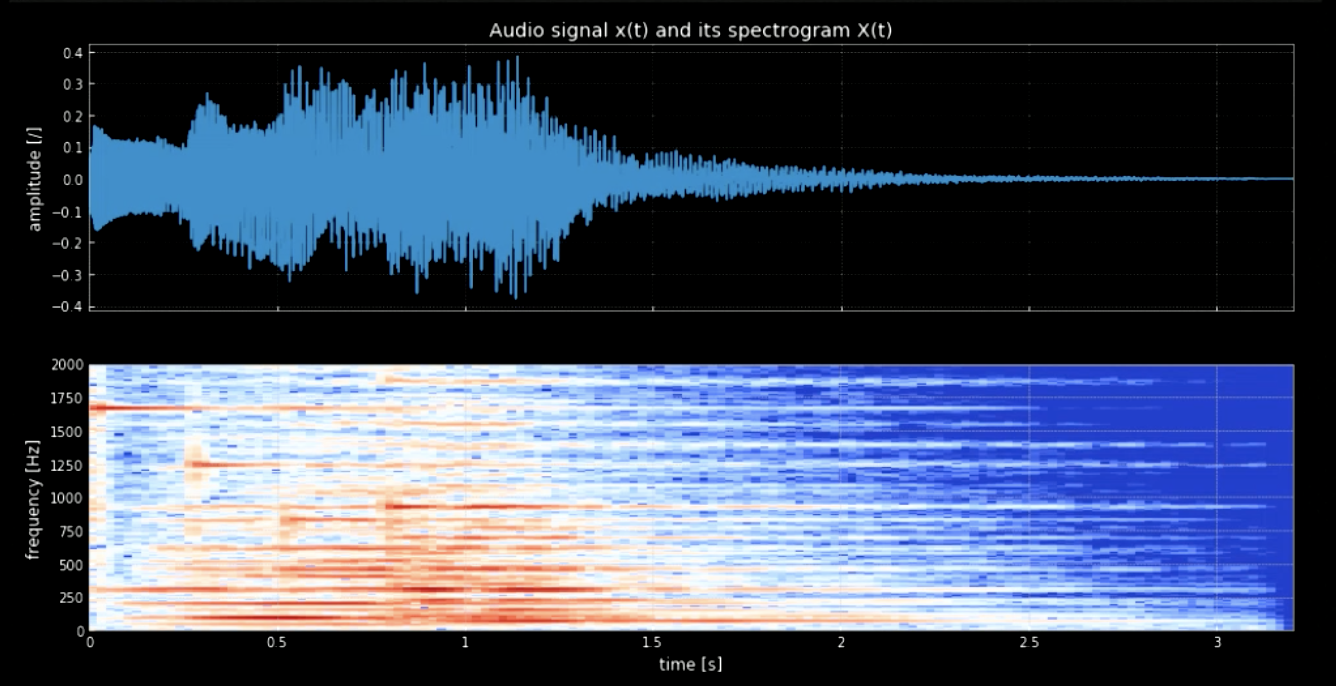
図3: 音声信号とそのスペクトログラム

入力信号とすべてのピッチ（たとえば、ピアノのすべての音階）を畳み込むと、入力（特定のカーネルが音声と一致したときに当たる）のすべての音符を抽出できます。 元の信号といろんなピッチを連結した信号のスペクトログラムを図4に、元の信号と4つのピッチの周波数を図5に示します。4つのカーネルを入力信号（元の信号）と畳み込みこんだものを図6に示します。図6と畳み込みされた信号のオーディオクリップが、ノートの抽出における畳み込みの有効性を証明しています。

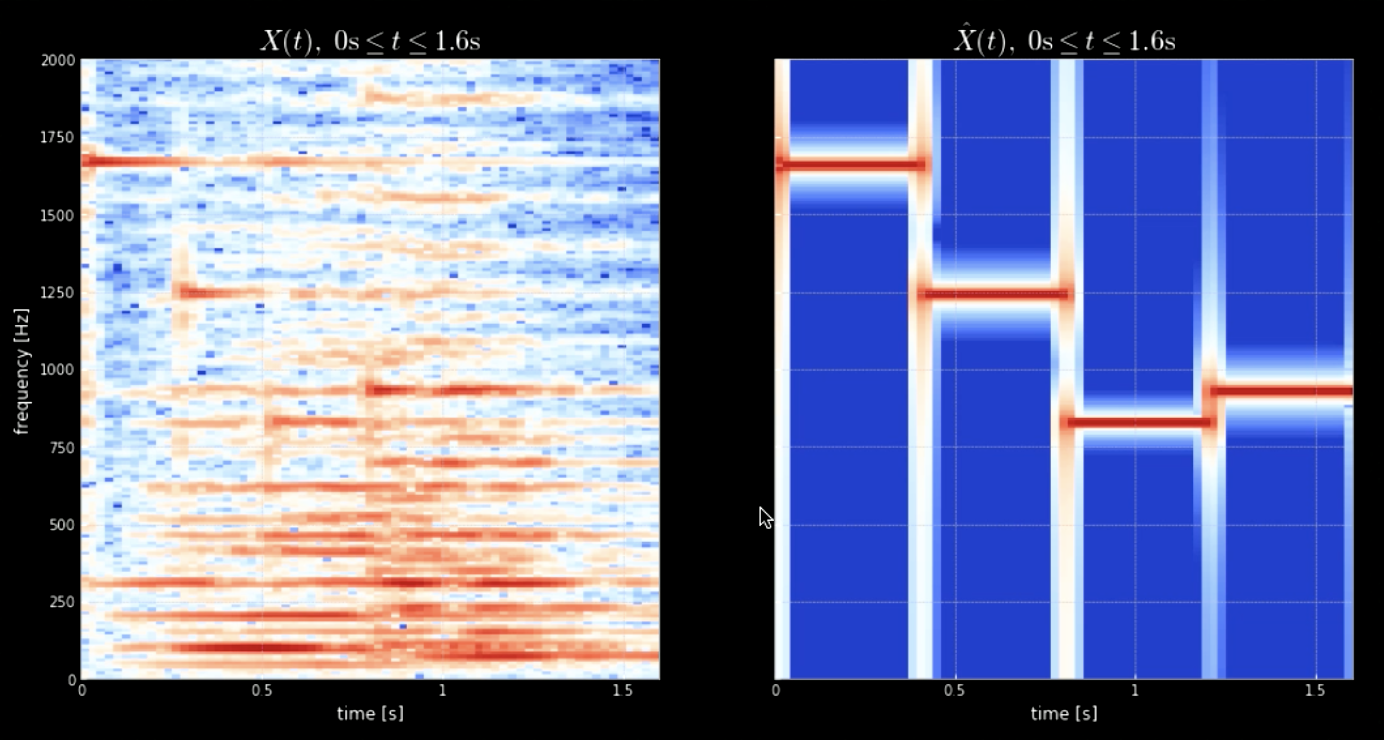
図4: 元の信号のスペクトログラム（左）とピッチが連結されたもののスペクトログラム（右）

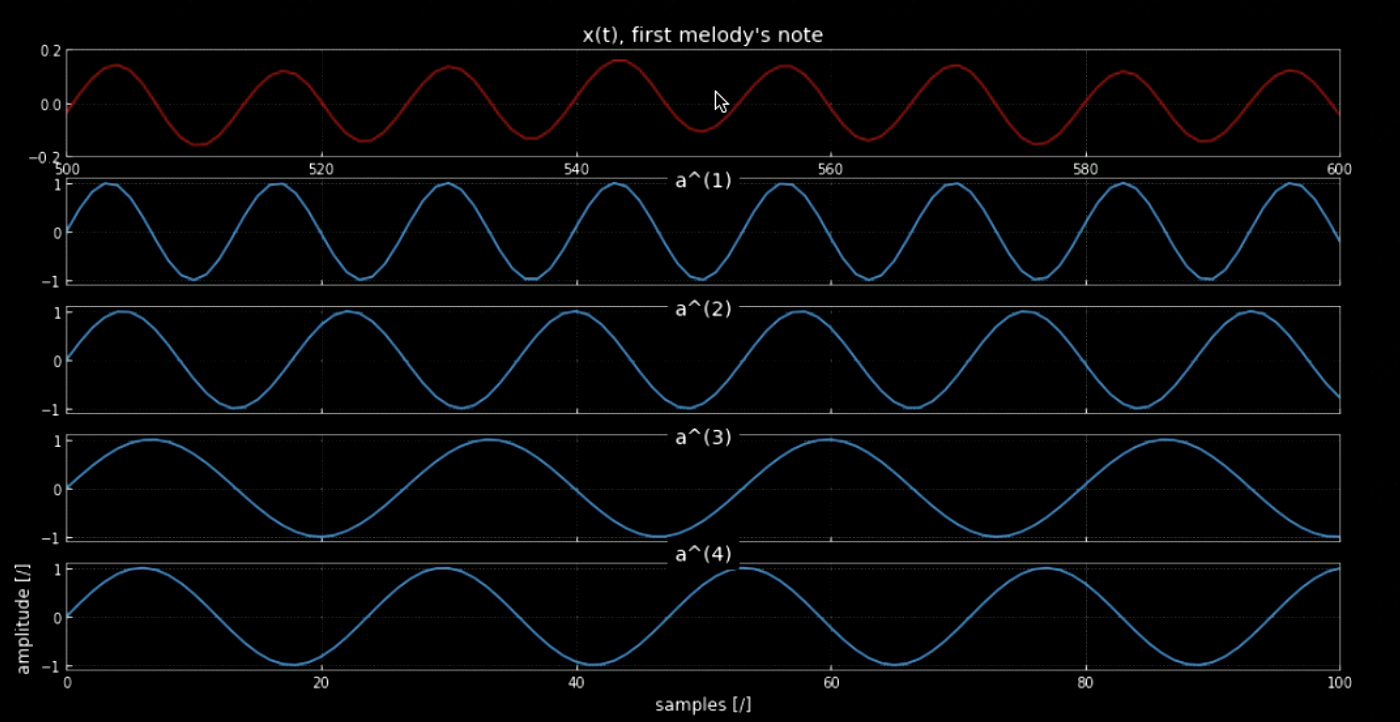
図5: メロディーの最初の音符.

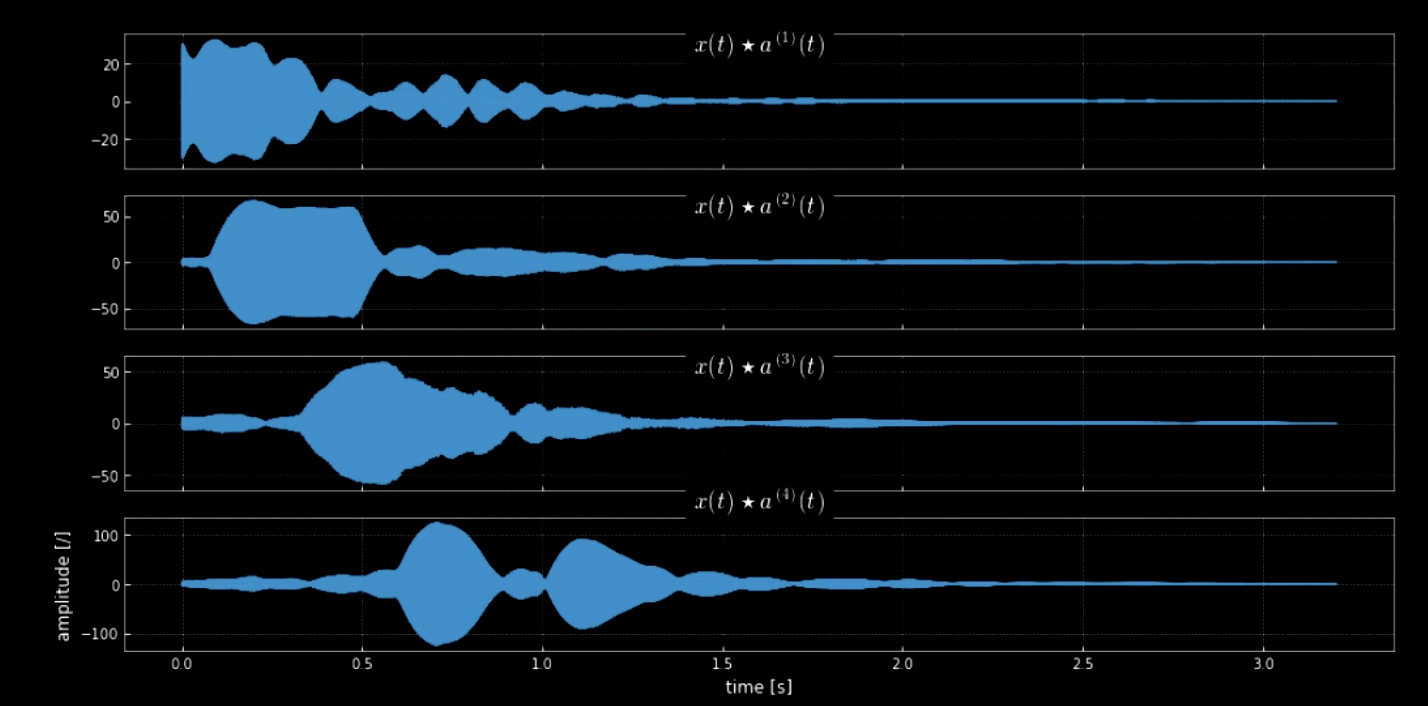
図6: 4つのカーネルの畳み込み

異なるデータセットの次元数

最後に、次元数のさまざまな表現とその例について、短い余談をします。 ここで、仮に入力セット$X$がドメイン$\Omega$からチャネル$c$にマッピングされたとします。

例

• 音声データ：ドメインは1次元; 時間でインデックス付けられた離散信号； チャネル数$c$は、1（モノ）、2（ステレオ）、5 + 1（ドルビー5.1）などがあります。
• 画像データ：ドメインは2次元（ピクセル）； $c$の範囲は、1（グレースケール）、3（カラー）、20（ハイパースペクトル）、などがあります。
• 特殊相対論：ドメインは$\mathbb{R^4} \times \mathbb{R^4}$（時空$\times$ 4モメンタム）です。 $c=1$の場合、ハミルトニアンと呼ばれます。

図7: 異なる信号の異なる次元

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
Jesmer Wong
18 Feb 2020