Metodi contrastivi nei modelli ad energia

Riassunto

Il dr. LeCun ha passato i primi 15 min circa riassumendo i modelli ad energia (energy based models, EBM). Si faccia riferimento alle lezioni della settimana scorsa (Settimana 7) per queste informazioni, specialmente per i concetti riguardanti i metodi di apprendimento contrastivo.

Come abbiamo appreso dall’ultima lezione, ci sono due classi principali di modelli per l’apprendimento ad energia:

1. Metodi contrastivi, che fanno decrescere l’energia dei dati di addestramento, $F(x_i, y_i)$, mentre la fanno decrescere nelle altre aree, $F(x_i, y’)$.
2. Metodi architettonici, che costruiscono la funzione di energia $F$ in modo tale da presentare poche o limitate regioni a bassa energia tramite l’applicazione di regolarizzazioni.

Al fine di distinguere le caratteristiche dei diversi metodi di addestramento, il dr. Yann LeCun ha inoltre sintetizzato 7 strategie di addestramento dalle categorie prima menzionate. Una di queste racchiude i metodi che sono simili al metodo di massima verosimiglianza (Maximum Likelihood).

La massima verosimiglianza diminuisce l’energia dei punti dei dati di addestramento e la diminuisce per tutti i punti $y’\neq y_i$ in maniera probabilistica. Essa non si “interessa” dei valori assoluti di energia, ma solamente della differenza fra le energie. Siccome le distribuzioni di probabilità sono sempre normalizzate affinché sommino o integrino a 1, comparare il rapporto tra due punti è più utile rispetto a comparare valori assoluti.

Metodi contrastivi nell’apprendimento auto-supervisionato

Nei metodi contrastivi, diminuiamo l’energia dei punti di addestramento ($x_i$, $y_i$), allo stesso momento aumentando l’energia dei punti esterni alla varietà dei dati.

Nell’appredimento auto-supervisionato (self-supervised learning, SSL), utilizziamo una parte dell’input per predirne le parte restanti. Speriamo che il nostro modello possa produrre delle buone caratteristiche per la visione artificiale in modo tale che possano competere con quelle ottenute dai compiti supervisionati.

I ricercatori hanno verificato in maniera empirica che l’applicazione dei metodi contrastivi di incorporazione (embedding) ai metodi di apprendimento auto-supervisionato può infatti portare a buone performance comparabili a quelle dei modelli supervisionati. Sotto esploreremo alcuni di questi metodi e vedremo i loro risultati.

Incorporamento contrastivo (Contrastive Embedding)

Si consideri una coppia ($x$, $y$) tale che $x$ sia un’immagine e $y$ una trasformazione di $x$ (rotazione, ingrandimento, ritaglio, ecc.) che ne preservi il contenuto. La denominiamo coppia positiva.

Fig. 1: coppia positiva

Concettualmente, l’incorporamento contrastivo prende una rete convoluzionale a cui dà in input $x$ e $y$, ottenendo due vettori di caratteristiche: $h$ e $h’$. Siccome $x$ e $y$ hanno lo stesso contenuto (ovvero, sono una coppia positiva), vogliamo che i loro vettori di caratteristiche siano più simili possibile. Perciò, scegliamo una metrica di similarità (come il coseno di similitudine) e una funzione di perdita che massimizzi la similarità fra $h$ e $h’$. Facendo ciò, abbassiamo l’energia per le immagini facenti parte della varietà dei dati di addestramento.

Fig. 2: coppia negativa

Tuttavia, dobbiamo ancora aumentare l’energia per i punti al di fuori di questa varietà. Quindi generiamo esempi negativi ($x_{\text{neg}}$, $y_{\text{neg}}$), ovvero immagini con diverso contenuto (ad esempio, aventi diversa categorizzazione). Le utilizziamo come input alla nostra rete di cui sopra, ottenendo i vettori di caratteristiche $h$ e $h’$, e proviamo a minimizzare la similarità fra di loro.

Questo metodo ci permette di “spingere” in basso l’energia di coppie simili, “spingendo” in alto l’energia di coppie dissimili.

Risultati recenti (su ImageNet) hanno mostrato che questo metodo può produrre caratteristiche valide per il riconoscimento di oggetti e che possono competere con quelle apprese tramite metodi supervisionati.

Risultati di metodi auto-supervisionati (MoCo, PIRL, SimCLR)

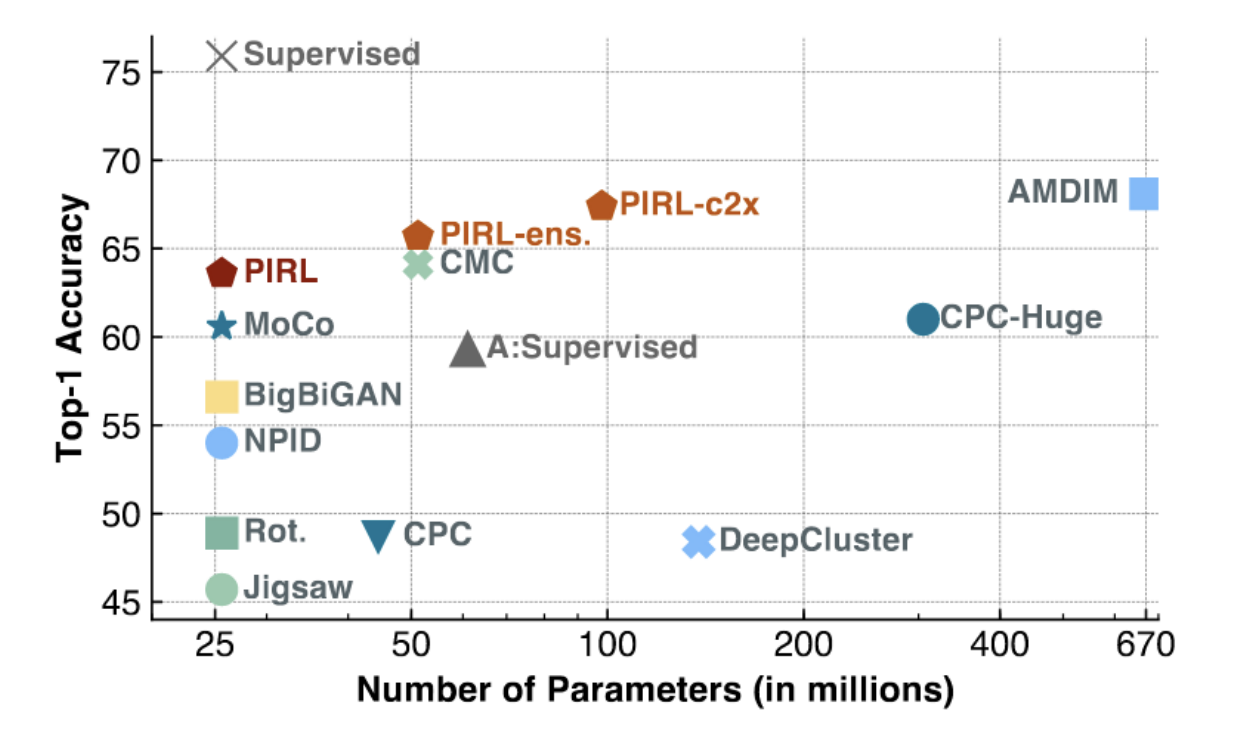
Fig. 3: PIRL e MoCo su ImageNet

Come vediamo dalla figura sopra, PIRL e MoCo ottengono risultati allo stato dell’arte (specialmente per modelli a bassa capacità, con un basso numero di parametri). PIRL sta iniziando ad avvicinarsi al livello di accuratezza di riferimento per i modelli supervisionati.

Possiamo comprendere PIRL un po’ meglio vedendo la sua funzione obiettivo: NCE (Noise Contrastive Estimator, stimatore contrastivo del rumore), come di seguito.

Qui utilizziamo il coseno di similarità come metrica di similarità fra due vettori/mappe di caratteristiche.

PIRL non utilizza direttamente l’output dell’estrattore convoluzionale di caratteristiche; definisce, invece, diversi “capi” $f$ e $g$, i quali possono essere concepiti come strati indipendenti da collocare al di sopra dell’estrattore convoluzionale di caratteristiche “di base”.

Componendo tutti i pezzi assieme, la funzione obiettivo di PIRL, NCE, funziona come di seguito. In un mini-batch abbiamo una coppia positiva (simile) e tante coppie negative (dissimili). Calcoliamo quindi la similarità tra il vettore di caratteristiche dell’immagine trasformate ($I^t$) e i restanti vettori delle caratteristiche del mini-batch (uno positivo, gli altri negativi). Dopodiché calcoliamo il punteggio di una funzione pseudo-esponenziale normalizzata (pseudo-softmax) sulla coppia positiva. Massimizzare il punteggio di una funzione softmax significa minimizzare i restanti punteggi, il che è esattamente il desiderata per i modelli basati sull’energia. La funzione di perdita finale, quindi, ci permette di costruire un modello che diminuisce l’energia per le coppie simili e l’aumenta per coppie dissimili.

Il dr. LeCun menziona il fatto che, affinché ciò funzioni, è richiesto un grande numero di coppie negative. Nell’SGD, può essere complicato mantenere costantemente un gran numero di queste coppie nei mini-batch. Di conseguenza, PIRL utilizza anche un banco di memoria temporanea fungente da “deposito”.

Domanda: perché utilizziamo il coseno di similarità anziché la norma L2? Risposta: con la norma L2 è molto facile rendere due vettori simili se corti (vicini al centro) o renderli dissimili se molto lunghi (lontani dal centro). Questo perché la norma L2 è una somma dei quadrati delle differenze parziali fra i due vettori. Di conseguenza, usando il coseno di similarità, si forza il sistema a trovare una buona soluzione senza “imbrogliare” rendendo i vettori corti o lunghi.

SimCLR

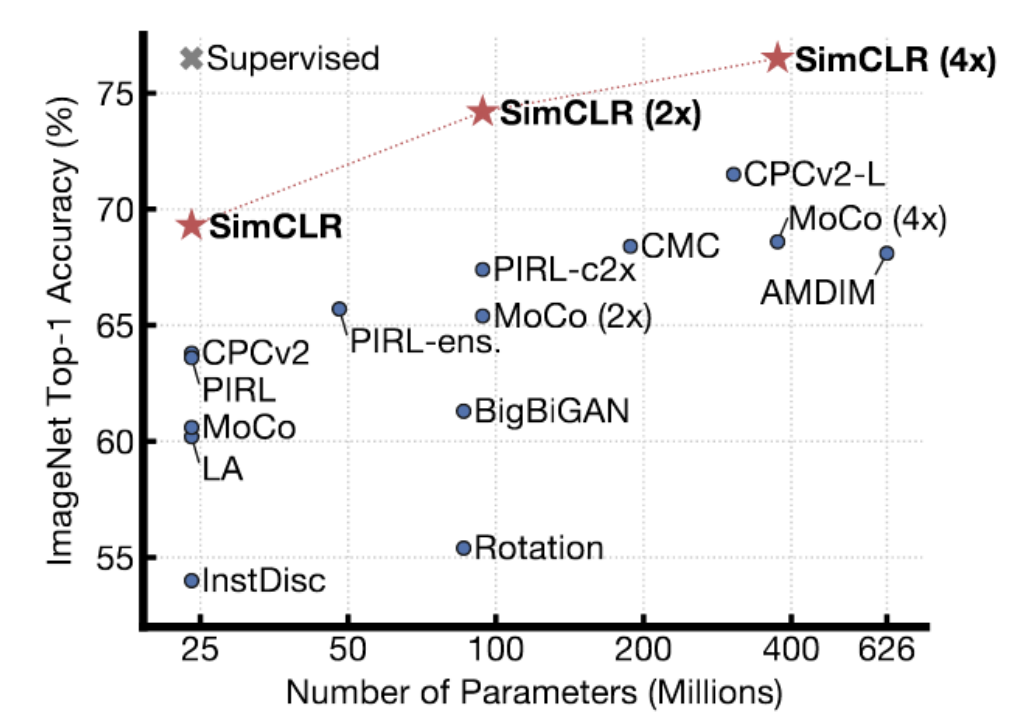
Fig. 4: risultati di SimCLR su ImageNet

SimCLR ha risultati migliori rispetto ai metodi precedenti. Infatti, raggiunge le performance dei metodi supervisionati su ImageNet. La sua tecnica utilizza un sofisticato metodo di aumento dei dati (data augmentation) per generare coppie simili; inoltre, viene addestrato per una quantità di tempo massiccia (con una grandezza del mini-batch molto elevata) sulle TPU. Il dr. LeCun crede che SimCLR mostri, in qualche misura, le limitazioni dei metodi contrastivi. Ci sono molte, molte regioni di uno spazio ad alta dimensionalità dove bisogna incrementare l’energia per assicurarsi che sia maggiore di quella della varietà dei dati. All’aumentare delle dimensioni della rappresentazione, si necessita di un numero sempre crescente di campioni negativi affinché ci si possa assicurare che l’energia sia più alta in quei luoghi dello spazio non appartenenti alla varietà.

Autoencoder per la riduzione del rumore (denoising autoencoder)

Nella pratica della settimana 7, abbiamo discusso degli autoencoder per la riduzione del rumore (denoising autoencoder). Questo modello tende ad apprendere la rappresentazione dei dati tramite ricostruzione di un input perturbato nell’input originale. Più specificamente, addestriamo il sistema a produrre una funzione di energia che cresce in maniera quadratica all’allontanarsi dei dati perturbati dalla varietà dei dati.

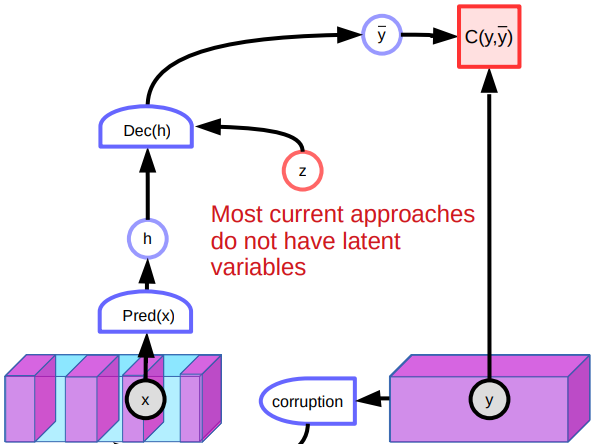
Fig. 5: architettura di un autoencoder per la riduzione del rumore

Problematiche

Tuttavia, ci sono anche numerosi problemi con gli autoencoder per la riduzione del rumore. Uno di questi è che in uno spazio continuo ad alta dimensionalità ci sono innumerevoli modi di perturbare un dato. Per cui, non ci sono garanzie che si possa dare forma alla funzione di energia semplicemente aumentandola in un gran numero di regioni dello spazio. Un altro problema con questo modello è che produce scarsi risultati con le immagini a causa della mancanza di variabili latenti. Siccome ci sono vari modi per ricostruire un’immagine, il sistema produce diverse previsioni e non impara caratteristiche particolarmente buone. Inoltre, i punti che, perturbati, rimangono all’interno della varietà, possono essere ricostruiti verso più direzioni. Questo creerà regioni piane all’interno della funzione di energia, le quali inficeranno la performance globale.

Altri metodi contrastivi

Ci sono altri metodi contrastivi come la divergenza contrastiva (contrastive divergence), la comparazione dei rapporti (ratio matching), la stima contrastiva del rumore (noise contrastive estimation) e il minimo flusso di probabilità (minumum probability flow). Daremo giusto un’infarinata riguardo l’idea base della divergenza contrastiva.

Divergenza contrastiva (contrastive divergence, CD)

La divergenza contrastiva è un altro modello che apprende le rappresentazioni tramite la perturbazione “intelligente” del campione di input. In uno spazio continuo, prima di tutto consideriamo un campione di addestramento $y$ e ne abbassiamo l’energia. Per questo campione, usiamo una sorta di processo basato sul gradiente per muoverci verso il basso sulla superficie dell’energia con rumore. Se lo spazio di input è discreto, possiamo invece perturbare il campione di addestramento in maniera casuale al fine di modificarne l’energia. Se l’energia risultante è più bassa, teniamo questa perturbazione; altrimenti, la scartiamo con un certo livello di probabilità. Facendo ciò risulterà, alla fine, nell’abbassamento dell’energia di $y$. Possiamo quindi aggiornare i parametri della nostra funzione di energia comparando $y$ e il campione contrastivo $\bar y$ tramite una qualche funzione di perdita.

Divergenza contrastiva persistente

Un affinamento della divergenza contrastiva è la divergenza contrastiva persistente. Il sistema utilizza una serie di “particelle” e ne memorizza la posizione. Queste particelle sono spostate verso il basso nella superficie dell’energia, in maniera analoga alla CD standard. Alla fine, troveranno dei luoghi a bassa energia nella nostra superficie dell’energia e ne causeranno un incremento dell’energia. Tuttavia, la tecnica non si adatta bene all’aumentare della dimensionalità.