Contrastive Methods in Energy-Based Models

Resumen

El Dr. LeCun pasó los primeros ~15 minutos dando una revisión de los modelos basados ​​en energía. Para obtener esta información, consulta los videos de la semana pasada (notas de la semana 7), especialmente el concepto de métodos de aprendizaje contrastivos (o de contraste).

Como hemos aprendido en la última clase, hay dos tipos principales de métodos de aprendizaje:

1. Métodos Contrastivos que reducen la energía de los puntos de datos de entrenamiento, $F(x_i, y_i)$, mientras aumentan la energía en cualquier otro lado, $F(x_i, y’)$.
2. Métodos Arquitectónicos que construyen la función de energía $F$ que ha minimizado / limitado las regiones de baja energía mediante la aplicación de regularización.

Para distinguir las características de los diferentes métodos de entrenamiento, el Dr. Yann LeCun ha resumido además 7 estrategias de entrenamiento de las dos clases mencionadas anteriormente. Uno de los cuales son los métodos similares al de Máxima Verosimilitud, que empujan hacia abajo la energía de los puntos de datos y empujan hacia arriba en todas las otras partes.

El método de máxima verosimilitud empuja probabilísticamente hacia abajo las energías en los puntos de datos de entrenamiento y empuja hacia todas partes cada otro valor de $y’\neq y_i$. Máxima Verosimilitud no “se preocupa” por los valores absolutos de las energías, sino que sólo “se preocupa” por la diferencia entre energías. Debido a que la distribución de probabilidad siempre se normaliza para sumar/integrar a 1, comparar la relación entre dos puntos de datos dados es más útil que simplemente comparar valores absolutos.

Métodos contrastivos en el aprendizaje auto-supervisado

En los métodos contrastivos, presionamos hacia abajo la energía de los puntos de datos de entrenamiento observados ($x_i$, $y_i$), mientras aumentamos la energía de los puntos fuera de la variedad (manifold) de datos de entrenamiento.

En el aprendizaje auto-supervisado, usamos una parte de la entrada para predecir las otras partes. Esperamos que nuestro modelo pueda producir buenas características (features) en el área de visión por computadora, que compitan con las de las tareas supervisadas.

Los investigadores han encontrado empíricamente que la aplicación de métodos de encaje contrastivos (contrastive embedding) a modelos de aprendizaje auto-supervisados puede tener buenos resultados que rivalizan con los de los modelos supervisados. Exploraremos algunos de estos métodos y sus resultados a continuación.

Encaje contrastivo

Considers un par ($x$, $y$), de modo que $x$ es una imagen e $y$ es una transformación de $x$ que conserva su contenido (rotación, ampliación, recorte, etc.). A esto lo llamamos un par positivo.

Fig. 1: Par Positivo

Conceptualmente, los métodos de inserción contrastivos toman una red convolucional y alimentan $x$ e $y$ a través de esta red para obtener dos vectores de características: $h$ y $h’$. Debido a que $x$ e $y$ tienen el mismo contenido (es decir, un par positivo), queremos que sus vectores de características sean lo más similares posible. Como resultado, elegimos una métrica de similitud (como la similitud del coseno) y una función de pérdida que maximiza la similitud entre $h$ y $h’$. Al hacer esto, disminuimos la energía de las imágenes en la variedad (manifold) de datos de entrenamiento.

Fig. 2: Par Negativo

Sin embargo, también tenemos que aumentar la energía de los puntos fuera de esta variedad. Así que también generamos muestras negativas ($x_{\text{neg}}$, $y_{\text{neg}}$), imágenes con contenido diferente (etiquetas de clase diferentes, por ejemplo). Los alimentamos a nuestra red anterior, obtenemos los vectores de características $h$ y $h’$, y ahora tratamos de minimizar la similitud entre ellos.

Este método nos permite empujar hacia abajo la energía de los pares similares, mientras empujamos hacia arriba la energía de pares diferentes.

Resultados recientes (en ImageNet) han demostrado que este método puede producir características que son buenas para el reconocimiento de objetos que pueden rivalizar con las características aprendidas a través de métodos supervisados.

Resultados Auto-Supervisados ​​(MoCo, PIRL, SimCLR)

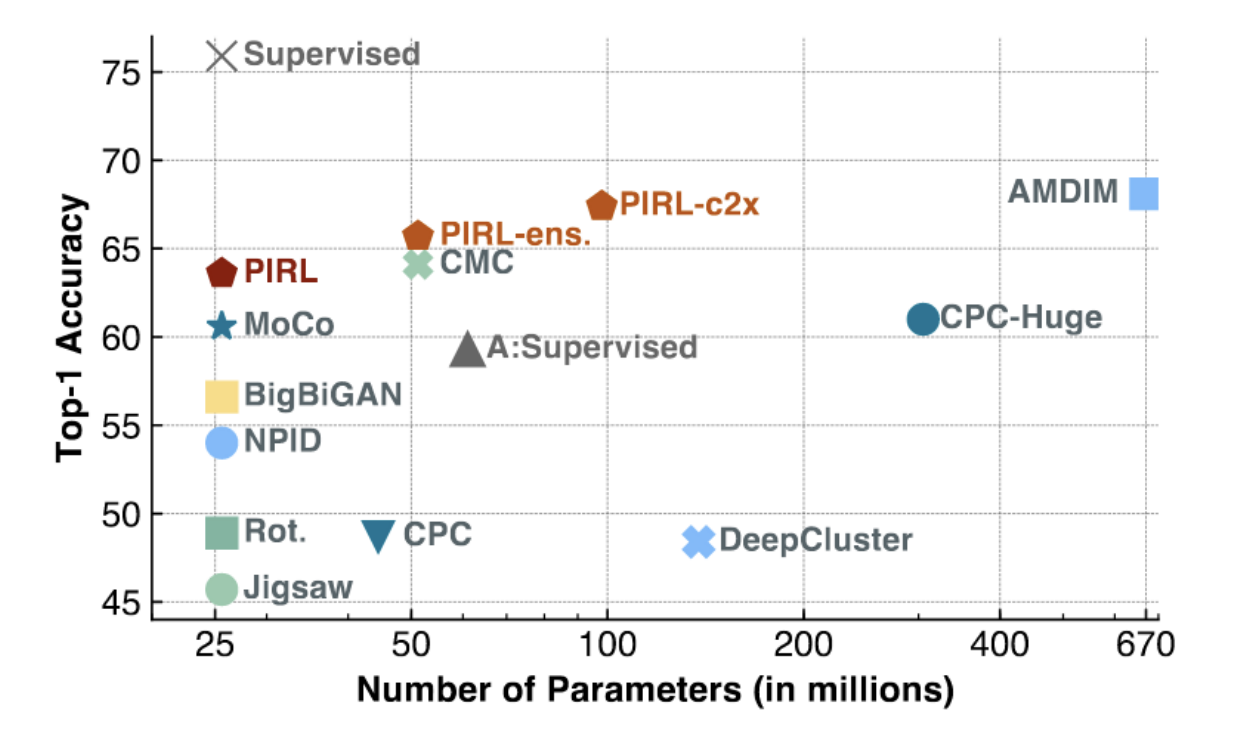
Fig. 3: PIRL y MoCo en ImageNet

Como se ve en la figura anterior, MoCo y PIRL logran resultados SOTA (especialmente para modelos de menor capacidad, con una pequeña cantidad de parámetros). PIRL está comenzando a acercarse al top-1 en precisión lineal de los modelos supervisados (~75%).

Podemos entender mejor a PIRL observando su función objetivo: NCE (Estimador de Contraste de Ruido) de la siguiente manera.

\(L_{\text{NCE}}(I,I^t)=-\log\Big[h\Big(f(v_I),g(v_{I^t})\Big)\Big]-\sum_{I'\in D_N}\log\Big[1-h\Big(g(v_{I^t}),f(v_{I'})\Big)\Big]\)

Aquí definimos la métrica de similitud entre dos mapas de características/vectores como la similitud del coseno.

Lo que hace PIRL de manera diferente es que no usa la salida directa del extractor de características convolucionales. En su lugar, define diferentes cabezas (heads) $f$ y $g$, que se pueden considerar como capas independientes sobre el extractor de características convolucionales base.

Poniendo todo junto, la función objetivo NCE de PIRL funciona de la siguiente manera. En un mini-lote, tendremos un par positivo (similar) y muchos pares negativos (diferentes). Luego calculamos la similitud entre el vector de características de la imagen transformada ($I^t$) y el resto de los vectores de características en el minibatch (uno positivo, el resto negativo). A continuación, calculamos la puntuación de una función similar a softmax en el par positivo. Maximizar una puntuación softmax significa minimizar el resto de las puntuaciones, que es exactamente lo que queremos para un modelo basado en energía. La función de pérdida final, por lo tanto, nos permite construir un modelo que empuja la energía hacia abajo en pares similares, mientras la empuja hacia arriba en pares diferentes.

El Dr. LeCun menciona que para que esto funcione, se requiere una gran cantidad de muestras negativas. En SGD, puede ser difícil mantener de manera consistente una gran cantidad de estas muestras negativas de mini lotes. Por lo tanto, PIRL también usa un banco de memoria en caché.

Pregunta: ¿Por qué utilizamos la similitud de coseno en lugar de la norma L2? Respuesta: Con una norma L2, es muy fácil hacer dos vectores similares haciéndolos “cortos” (cerca del centro) o hacer dos vectores diferentes haciéndolos muy “largos” (lejos del centro). Esto se debe a que la norma L2 es solo una suma de diferencias parciales cuadradas entre los vectores. Por lo tanto, el uso de la similitud de coseno obliga al sistema a encontrar una buena solución sin “hacer trampa” haciendo vectores cortos o largos.

SimCLR

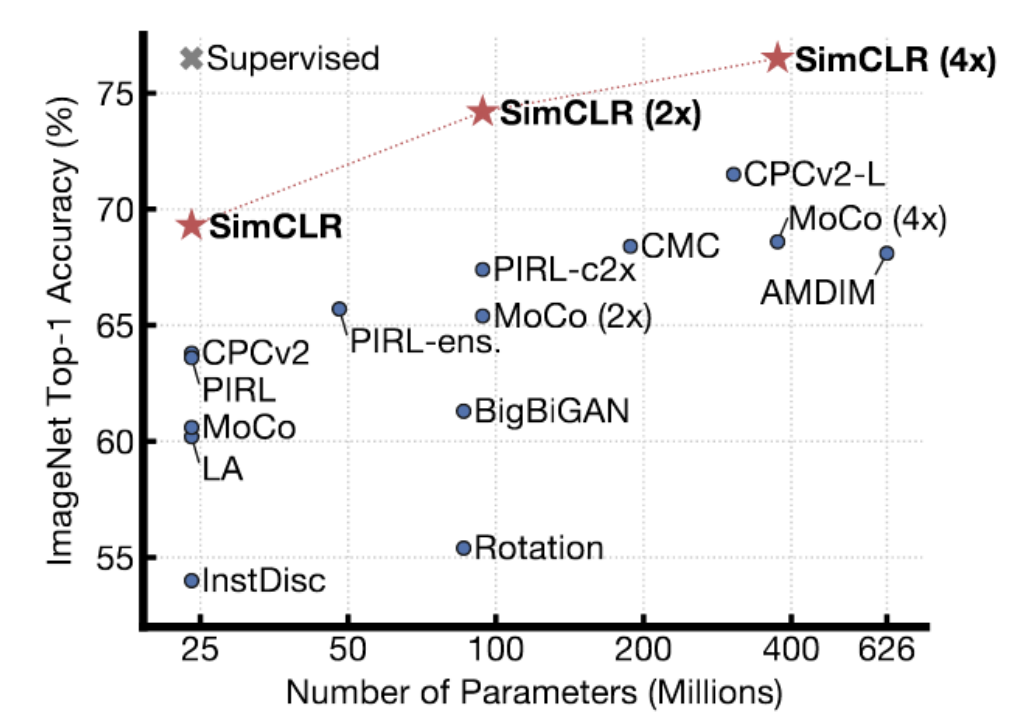
Fig. 4: Resultados de SimCLR en ImageNet

SimCLR muestra mejores resultados que los métodos anteriores. De hecho, alcanza el rendimiento de los métodos supervisados ​​en ImageNet, con una precisión lineal de primer nivel en ImageNet. La técnica utiliza un método sofisticado de aumento de datos para generar pares similares, y lo entrenan durante una gran cantidad de tiempo (con tamaños de lote muy, muy grandes) en TPUs. El Dr. LeCun cree que SimCLR, hasta cierto punto, muestra el límite de los métodos contrastivos. Hay muchas, muchas regiones en un espacio de alta dimensión en las que necesita aumentar la energía para asegurarse de que sea realmente más alta que en la variedad de datos. A medida que aumenta la dimensión de la representación, necesita más y más muestras negativas para asegurarse de que la energía sea mayor en esos lugares que no pertenecen al manifold.

Denoising autoencoder

En la práctica de la semana 7, hablamos sobre denoising autoencoders. El modelo tiende a aprender la representación de los datos reconstruyendo la entrada dañada en la entrada original. Más específicamente, entrenamos al sistema para producir una función de energía que crece cuadráticamente a medida que los datos corruptos se alejan de la variedad de los datos.

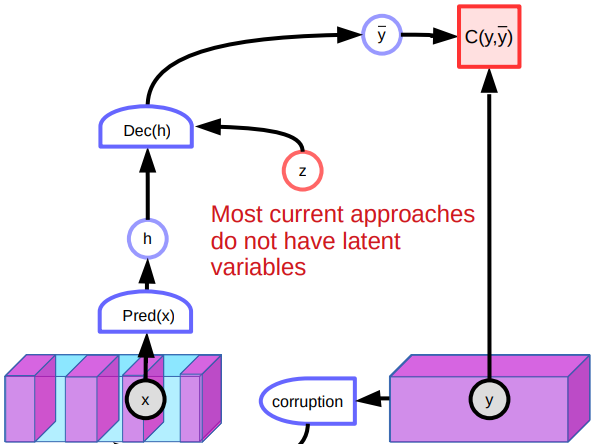
Fig. 5: Architectura del *denoising autoencoder*

Problemas

Sin embargo, existen varios problemas con la eliminación de ruido de los codificadores automáticos. Un problema es que en un espacio continuo de alta dimensión, existen incontables formas de corromper un dato. Por lo tanto, no hay garantía de que podamos dar forma a la función de energía simplemente presionando hacia arriba en muchos lugares diferentes. Otro problema con el modelo es que funciona mal cuando se trata de imágenes debido a la falta de variables latentes. Dado que hay muchas formas de reconstruir las imágenes, el sistema produce varias predicciones y no aprende características particularmente buenas. Además, los puntos corruptos en el medio del manifold podrían reconstruirse a ambos lados. Esto creará puntos planos en la función de energía y afectará el rendimiento general.

Otros Métodos Contrastivos

Existen otros métodos contrastivos como la divergencia contrastiva, la correspondencia de relaciones (Ratio Matching), la estimación contrastante de ruido y el flujo de probabilidad mínimo. Discutiremos brevemente la idea básica de divergencia contrastiva.

Divergencia Contrastiva

La divergencia contrastiva (CD) es otro modelo que aprende la representación corrompiendo inteligentemente la muestra de entrada. En un espacio continuo, primero elegimos una muestra de entrenamiento $y$ y reducimos su energía. Para esa muestra, usamos algún tipo de proceso basado en gradientes para movernos hacia abajo en la superficie de energía con ruido. Si el espacio de entrada es discreto, podemos perturbar la muestra de entrenamiento al azar para modificar la energía. Si la energía que obtenemos es menor, la conservamos. De lo contrario, lo descartamos con cierta probabilidad. Seguir haciéndolo eventualmente reducirá la energía de $y$. Luego podemos actualizar el parámetro de nuestra función de energía comparando $y$ y la muestra contrastada $\bar y$ con alguna función de pérdida.

Divergencia Contrastiva Persistente

Uno de los refinamientos de la divergencia contrastiva es la divergencia contrastiva persistente. El sistema usa un montón de “partículas” y recuerda sus posiciones. Estas partículas se mueven hacia abajo en la superficie de energía al igual que lo hicimos en divergencia contrastiva normal (CD). Eventualmente, encontrarán lugares de baja energía en nuestra superficie energética y harán que sean empujadas hacia arriba. Sin embargo, el sistema no escala bien a medida que aumenta la dimensionalidad.