شرح عمليات الإلتفاف و جهاز التفاضل التلقائي

فهم الإلتفاف في بعد واحد (Understanding 1D convolution)

في هذا الجزء سوف نقوم بمناقشة الإلتفاف لأننا نريد أن نستكشف إنتشارية (sparisty) و ثباتية (stationarity) و تكوينية (compositionality) البيانات.

بدلاً عن استخدام المصفوفة $A$ التي تم مناقشتها في العمل السابق سوف نغير عرض المصفوفة إلى حجم النواة $k$. بالتالي أي صف في المصفوفة يمثل نواة. يمكننا استخدام هذه الأنوية عن طريق تجميعهم وإزاحتهم (انظر إلى شكل 1). إذًا، لدينا $m$ من الطبقات بإرتفاع $n-k+1$.

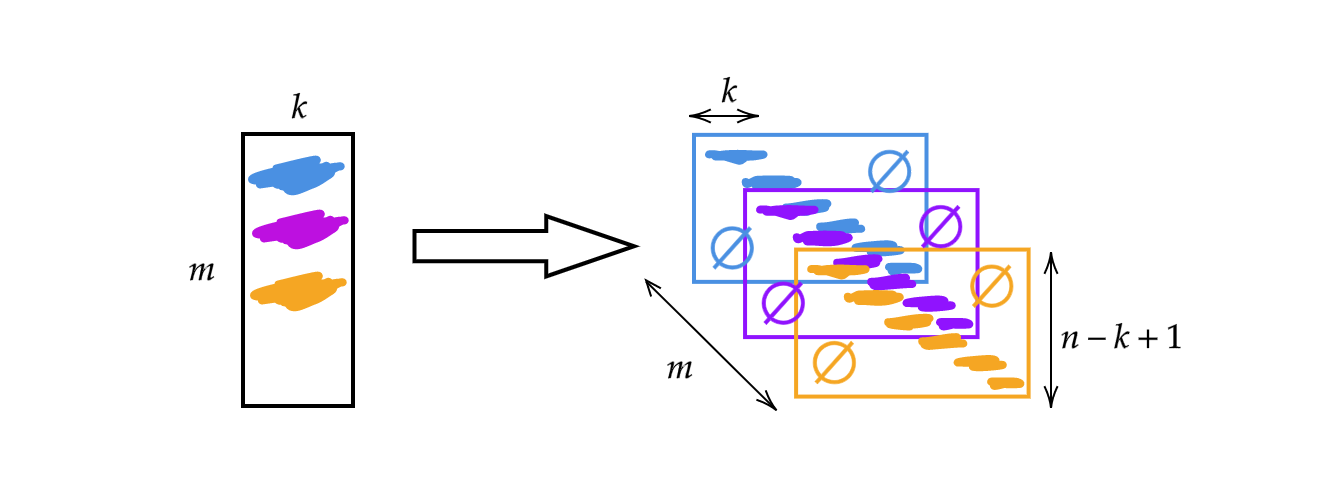
شكل 1: توضيح للإلتفاف ذو البعد الواحد (1D)

المخرج هو $m$ (سماكة) المتجهات التي حجمها $n-k+1$.

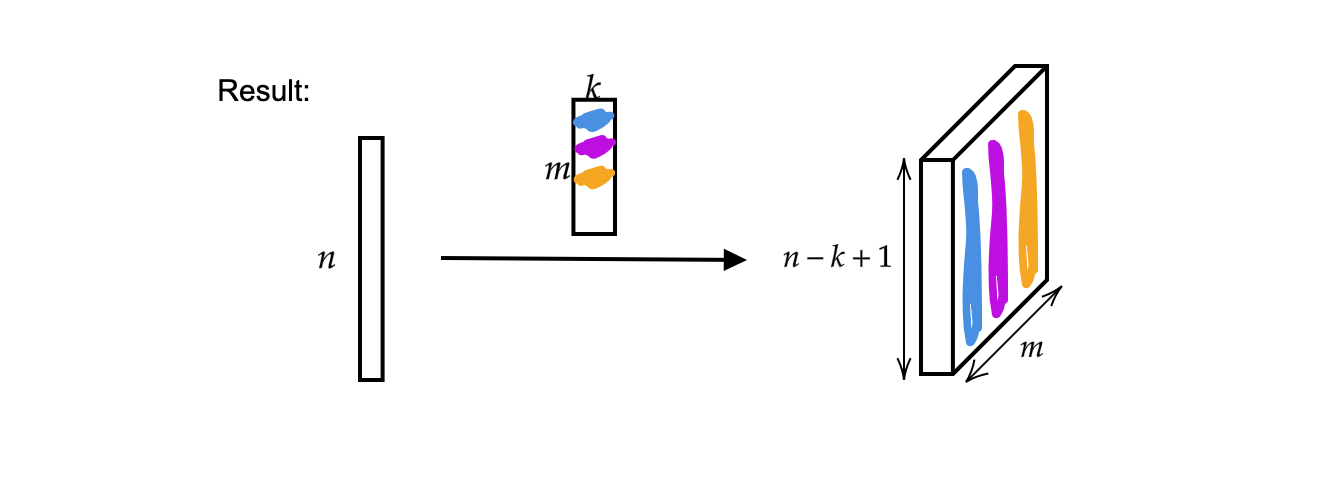
شكل 2 : نتيجة الإلتفاف 1D

أيضا مدخل واحد يمكن أن ينظر إليه كموجة أحادية الصوت

شكل 3: موجة أحادية الصوت

الآن المدخل $x$ هو عبارة عن تحويل

حيث $\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb{N}^1$ (لأن هذه موجة ذات بعد واحد أو مجال ذو بعد واحد) و في هذه الحالة رقم القناة $c$ هو $1$. عندما $c$ = $2$ فإن الموجة تصبح موجة ستيريو .

أبعاد الأنوية (kernels) و عرض المخرجات في PyTorch

تلميح: يمكننا استخدام question mark في IPython للحصول على مستندات الدوال. مثلاً

Init signature:
nn.Conv1d(
	in_channels,           # number of channels in the input image
	out_channels,          # number of channels produced by the convolution
	kernel_size,           # size of the convolving kernel
	stride=1,              # stride of the convolution
	padding=0,             # zero-padding added to both sides of the input
	dilation=1,            # spacing between kernel elements
	groups=1,              # nb of blocked connections from input to output
	bias=True,             # if `True`, adds a learnable bias to the output
	padding_mode='zeros',  # accepted values `zeros` and `circular`
)

الإلتفاف ذو البعد الواحد

لدينا إلتفاف ذو بعد $1$ من $2$ من القنوات (موجة ستيريو) إلى $16$ قناة ($16$ أنوية) بحجم نواة $3$ و طول خطوة $1$. و بعد ذلك لدينا $16$ أنوية بسمك $2$ و طول $3$. لنفترض أن الموجة المدخلة لديها طول حزمة $1$ (موجة واحدة) و $2$ من القنوات و $64$ عينة. الطبقة المخرجة الناتجة لديها $1$ موجة و $16$ قناة و طول الموجة $62$ (حيث أن $64-3+1$). أيضا أذا أخرجنا حجم معامل الإنحياز سوف نجد أن حجم معامل الإنحياز هو $16$ لأننا لدينا معامل إنحياز واحد لكل وزن.

conv = nn.Conv1d(2, 16, 3)  # 2 channels (stereo signal), 16 kernels of size 3
conv.weight.size()          # output: torch.Size([16, 2, 3])
conv.bias.size()            # output: torch.Size([16])

x = torch.rand(1, 2, 64)    # batch of size 1, 2 channels, 64 samples
conv(x).size()              # output: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2 channels, 16 kernels of size 5
conv(x).size()              # output: torch.Size([1, 16, 60])

الإلتفاف ذو البعدين

أولاً نعرف البيانات المدخلة كـ $1$ عينة و$20$ قناة (افترض أنها صورة لديه أطياف عدة) بإرتفاع $64$ وعرض $128$. فأن الإلتفاف ذو بعدين يكون لديه $20$ قناة من المدخل و$16$ نواة بحجم $3 \times 5$. بعد تطبيق الإلتفاف فأن البيانات المخرجة لديها $1$ عينة و $16$ قناة بإرتفاع $62$ (حيث أن $64-3+1$) و عرض $124$ (لأن $128-5+1$).

x = torch.rand(1, 20, 64, 128)    # 1 sample, 20 channels, height 64, and width 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 channels, 16 kernels, kernel size is 3 x 5
conv.weight.size()                # output: torch.Size([16, 20, 3, 5])
conv(x).size()                    # output: torch.Size([1, 16, 62, 124])

إذا أردنا أن نصل إلى نفس البعد يمكننا استخدام تبطينات. في الكود أعلاه، يمكننا إضافة عوامل لدالة الإلتفاف stride=1 و padding=(1, 2) و هذا يعني $1$ في إتجاه $y$ (واحد في الأعلى وواحد في الأسفل) و $2$ في إتجاه $x$. بالتالي تكون الموجة المخرجة يكون لها نفس الحجم مقارنة بالموجة المدخلة. عدد الأبعاد المطلوب لتخزين مجموعة الأنوية عندما نستعمل إلتفاف ذو بعدين هو $4$.

# 20 channels, 16 kernels of size 3 x 5, stride is 1, padding of 1 and 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # output: torch.Size([1, 16, 64, 128])

كيف يعمل حساب الإنحدار التلقائي

في هذ الجزء سوف نطلب من torch تفحص كل الحسابات على الموترات (tensors) حتى نتمكن من حساب التفاضلات الجزئية.

• عرف موتر $\boldsymbol{x}$ بالأبعاد $2\times2$ مع إمكانية تجميع الإنحدار.
• إطرح $2$ من كل عناصر $\boldsymbol{x}$ لنحصل على $\boldsymbol{y}$ (إذا طبعنا y.grad_fn فسوف يكون المخرج <SubBackward0 object at 0x12904b290> و هذا يعني أن y تساوي القيمة المطلقة لحاصل الطرح $\boldsymbol{x}-2$. أيضاً يمكننا استخدام y.grad_fn.next_functions[0][0].variable لنشتق الموتر الأصلي.)
• قم بالمزيد من الحسابات: $\boldsymbol{z} = 3\boldsymbol{y}^2$;
• أحسب متوسط $\boldsymbol{z}$.

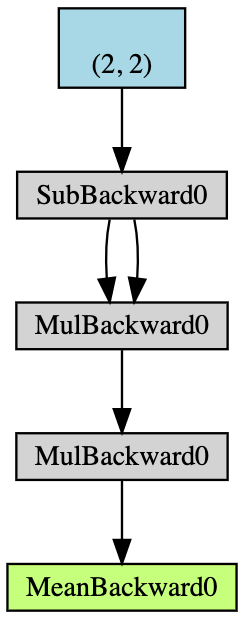
شكل 5: مخطط لمثال التدرج التلقائي

يستخدم الانتشار الخلفي لحساب التدرجات. في هذا المثال، يمكن النظر إلى عملية الانتشار الخلفي على أنها حساب التدرج $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$. بعد حساب $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$ يدويًا للتحقق من الصحة، يمكننا أن نجد أن تنفيذ a.backward() يعطينا نفس القيمة x.grad في حساباتنا.

فيما يلي عملية حساب الانتشار الخلفي يدويًا:

عندما تريد استخدام التفاضل الجزئي في PyTorch سوف تحصل على نفس أبعاد البيانات. لكن المصفوفة الجاكوبية الصحيحة هي منقولها (transpose).

من الأساسيات إلى الأكثر جنوناً

الآن لدينا متجه بأبعاد $1\times3$ والمسمى بـ $x$، قم بتعيين $y$ لضعف $x$ واستمر في مضاعفة $y$ حتى يصبح معياره (norm) أصغر من $1000$. نظرًا للعشوائية التي لدينا لـ $x$، لا يمكننا معرفة عدد التكرارات بشكل مباشر بعد إنتهاء هذا الإجراء.

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

لكن يمكننا أن نتوقعها بسهولة إذا عرفنا قيم الإنحدارات.

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

كما في عملية التوقع فإننا نستخدم requires_grad=True لنوضح أننا نريد متابعة مجموع الإنحدارات كما موضح أدناه. إذا كنا قمنا بإزالة requires_grad=True في حالة تعريف $x$ أو $w$ و استخدام backward() على $z$ فسينتج خطأ في زمن التنفيذ ﻷنه ليس لدينا مجموع إنحدارات لـ $x$ أو $w$.

# Both x and w that allows gradient accumulation
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

و يمكن استخدام with torch.no_grad() لتجاهل مجموع الإنحدارات.

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# All torch tensors will not have gradient accumulation
with torch.no_grad():
    z = w @ x

try:
    z.backward()  # PyTorch will throw an error here, since z has no grad accum.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

جزء إضافي – الإنحدار المخصص

أيضاً بدلاً عن العمليات العددية الأساسية فأننا يمكن أن نعمل دوال أو وحدات خاصة بنا و التي يمكن أن نستعملها في الشبكة العصبية. يمكن أن تجد الـ Jupyter Notebook هنا.

لنفعل ذلك نحتاج لأن نرث الكلاس torch.autograd.Function و نعيد تعريف الدوال forward() و backward(). مثلاً إذا كنا نريد تدريب شبكة ما فأننا نحتاج إلى أن نمرر المدخل عبر الشبكة و نعرف التفاضلات الجزئية للمدخل بالنسبة للمخرج لذلك يمكننا استخدام هذه الوحدة في أي نقطة في الكود. ثم باستخدام الإنتشار الخلفي (قاعدة السلسلة) يمكننا استخدام هذه الوحدة في أي مكان في سلسلة العمليات طالماً أننا نعلم التفاضلات الجزئية للمدخل بالنسبة للمخرج.

في هذه الحالة لدينا تلاتة أمثلة للوحدات المخصصة في هذا الـ notebook الوحدات add و split و max. مثلاً الوحدة المخصصة للجمع:

# Custom addition module
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx is a context where we can save
        # computations for backward.
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # need to return grads in order
        # of inputs to forward (excluding ctx)
        return grad_x1, grad_x2

إذا كان لدينا حاصل جمع شيئين والمخرج واحد فنحتاج إلى إعادة تعريف دالة الـ forward بهذه الطريقة. ولما نعود للأسفل للقيام بالإنشار الخلفي فإن الإنحدارات يتم نسخها عبر الجهتين. لذلك نعيد تعريف دالة الـ backward عن طريق النسخ.

بالنسبة إلى split وmax، راجع الكود الخاص بكيفية كتابة دالة الـ forward و الـ backward في هذه المذكرة. إذا أتينا من نفس الشيء و قمنا بالانقسام عند النزول لعمل التدرجات، يجب أن نجمعها. بالنسبة لـ argmax، فإنه يحدد مؤشر الشيء الأعلى، لذلك يجب أن يكون المؤشر الأعلى هو $1$ بينما يكون الآخر $0$. تذكر أن وفقًا للوحدات النمطية المختلفة، نحتاج إلى إعادة تعريف دالة الـ forward الخاصة بها، وكيفية حساب التدرجات في دالة الـ backward.