الجبر الخطي و الالتفاف

🎙️ Alfredo Canziani

مراجعة الجبر الخطي

هذا الجزء مراجعة للجبر الخطي ضمن صياغ الشبكات العصبية. فلنبدأ بطبقة مخفية واحدة $\boldsymbol{h}$:

\[\boldsymbol{h} = f(\boldsymbol{z})\]

الناتج هو دالة غير خطية $f$ مطبقة على المتجه $z$. هنا $z$ عبارة عن مخرج التحويل التآلفي $\boldsymbol{A} \in\mathbb{R^{m\times n}}$ للمتجه $\boldsymbol{x} \in\mathbb{R^n}$:

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

لتبسيط التحويل سنتجاهل الحدود المطلقة، لتصبح المعادلات هكذا:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

حيث تمثل $i$ في $\boldsymbol{a}^{(i)}$ رقم الصف في المصفوفة $\boldsymbol{A}$.

حتى نفهم المعنى وراء هذا التحويل، علينا أن نحلل إحدى مكونات $\boldsymbol{z}$، على سبيل المثال $a^{(1)}\boldsymbol{x}$. دع $n=2$، و من ثم $\boldsymbol{a} = (a_1,a_2)$ و $\boldsymbol{x} = (x_1,x_2)$.

يمكن رسم $\boldsymbol{a}$ و $\boldsymbol{x}$ كمتجهين في نظام إحداثي ثنائي الأبعاد. الآن. إذا كانت الزاوية بين $\boldsymbol{a}$ و $\hat{\boldsymbol{\imath}}$ هي $\alpha$ و الزاوية بين $\boldsymbol{x}$ و $\hat{\boldsymbol{\imath}}$ هي $\xi$, عندها الصيغة المثلثية $a^\top\boldsymbol{x}$ تصبح:

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

يقيس الناتج مدى محاذاة المدخل بالنسبة لصف معين من المصفوفة $\boldsymbol{A}$. بإمكاننا فهم ذلك بملاحظة الزاوية بين المتجهين، $\xi-\alpha$. عندما يكون $\xi = \alpha$، نجد أن المتجهان متحاذيان تماماً و الناتج يكون في أقصى قيمه. أما إذا $\xi - \alpha = \pi$، عندها $\boldsymbol{a}^\top\boldsymbol{x}$ تصل أدنى قيمها و المتجهان يشيران إلى إتجاهين متعاكسين. كخلاصة، التحويل الخطي يمكننا من إسقاط المدخل على محاور مختلفة مُعرفة بدلالة المصفوفة $A$. يمكن استخدام هذا التفسير للأبعاد العليا أيضاً.

بطريقة أخرى نستطيع فهم التحويل الخطي بأن $\boldsymbol{z}$ يمكن إعادة صياغتها كما يلي:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

يمثل المخرج مجموع أوزان أعمدة المصفوفة $\boldsymbol{A}$. ولذلك فإن الإشارات الناتجة ليست إلا تركيبة من المدخل.

من الجبر الخطي إلى الالتفاف

سنقوم الآن بالتوسع والانتقال من التحويل الخطي إلى الالتفاف، مستخدمين تحليل البيانات الصوتية كمثال. بداية، نقوم بتمثيل الطبقة كلية الإتصال بعمليات الضرب:

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

في هذا المثال، مصفوفة الأوزان بالأبعاد $4 \times 3$، و المتجه المدخل بالأبعاد $3 \times 1$ و المتجه المخرج بالأبعاد $4 \times 1$.

و لكن, بالنسبة للبيانات الصوتية، عادة ما تكون البيانات أطول بكثير (ليست 3 عينات فقط). عدد العينات للبيانات الصوتية تساوي مدة المقطع الصوتي (في هذا المثال 3 ثوان) مضروبة في معدل أخذ العينات (في هذا المثال 22.05 كيلو هرتز). يعد المتجه المدخل $\boldsymbol{x}$ طويلاً كما هو موضح أدناه. و بالمثل, مصفوفة الأوزان ستأخذ مساحة كبيرة.

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

بالتالي الصيغة أعلاه صعبة للتدريب. ولحسن الحظ بإمكاننا تبسيطها.

خاصية المحلية

بسبب المحلية (وهي عدم الإكتراث بالنقاط البعيدة في البيانات عن نقطتنا هذه) يمكن استبدال البيانات $w_{1k}$ في مصفوفة الأوزان أعلاه بالأصفار عندما تكون $k$ كبيرة كفاية. عندها، يصبح الصف الأول للمصفوفة مرشحاً بطول 3. فلنسم هذا المرشح بالرمز $\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$.

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

خاصية السكون

تمتلك موجات البيانات الطبيعة خاصية الثبات (إذ تتكو عدد من الأنماط الثابتة فيها). يساعدنا ذلك في إعادة استخدام المرشح $\mathbf{a}^{(1)}$ المعرف مسبقاً. نستخدم المرشح بتحريكه خطوة عند كل مرة (كل خطوة انتقالية تساوي 1), منتجاً الآتي:

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

يمتلئ الجزء العلوي والسفلي من المصفوفة بالأصفار بسبب المحلية، مما يؤدي إلى تناثر القيم التي لا تساوي صفر. إعادة استخدام مرشح معين باستمرار يسمى بمشاركة الأوزان.

الطبقات المتعددة لمصفوفة توبلتز (Toeplitz)

بعد تلك التغييرات، يثبح عدد المعاملات المتبقية مساويًا إلى 3 (وهي $a_1,a_2,a_3$). بالمقارنة المصفوفة السابقة ذات الـ 12 معاملًا ($w_{11},w_{12},\cdots,w_{43}$)، نجد أن عدد المعاملات الحالي مقيد جداً ولذلك يجب نمدده للوصول لنفس العدد.

تعتبر المصفوفة السابقة طبقة بحد زاتها (طبقة التفافية) مع المرشح $\boldsymbol{a}^{(1)}$. عندها يمكننا أن نبني عدة طبقات باستخدام مرشحات مختلفة $\boldsymbol{a}^{(2)}$، $\boldsymbol{a}^{(3)}$، الخ، وبالتالي نزيد من عدد المعاملات.

كل طبقة تحتوي على مرشح واحد فقط مكرر عدة مرات. يدعى هذا النوع من المصفوفات مصفوفة توبلتز. في كل مصفوفة من هذا النوع، تمثل عناصر كل قطر نازل من اليسار إلى اليمين ذات الثابت. مصفوفات توبلتز المستخدمة هنا هي مصفوفة متناثرة القيم.

باعتبار المرشح الأول كمعطى $\boldsymbol{a}^{(1)}$ و كذلك المتجه المدخل $\boldsymbol{x}$، أول عنصر بالناتج من هذه الطبقة هو $a_1^{(1)} x_1 + a_2^{(1)} x_2 + a_3^{(1)}x_3$. ومنها يصبح المتجه الناتج:

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

يمكن استعمال ذات الصيغة في الطبقات الالتفافية التالية ($\boldsymbol{a}^{(2)}$ و $\boldsymbol{a}^{(3)}$) للحصول على نتائج مشابهة.

الاستماع للالتفاف - Jupyter Notebook

يمكنك إيجاد الملف هنا.

في الملف أعلاه, سنكتشف الالتفاف كـ ‘ضرب نقطي متحرك’.

المكتبة librosa ستمكننا من تحميل المقطع الصوتي $\boldsymbol{x}$ و معدل أخذ العينات. في هذه الحالة، هناك 70641 عينة، و معدل أخذ العينات هو 22.05 كيلو هرتز، كما أن زمن المقطع هو 3.2 ثوان. المقطع المحمل متموج (انظر الشكل 1) ويمكننا أن نتوقع الصوت بالنظر إالى قيم المحور $y$ . الإشارة الصوتية $x(t)$ هو الصوت الذي يصدر عن إغلاق نظام ويندوز (انظر الشكل 2).

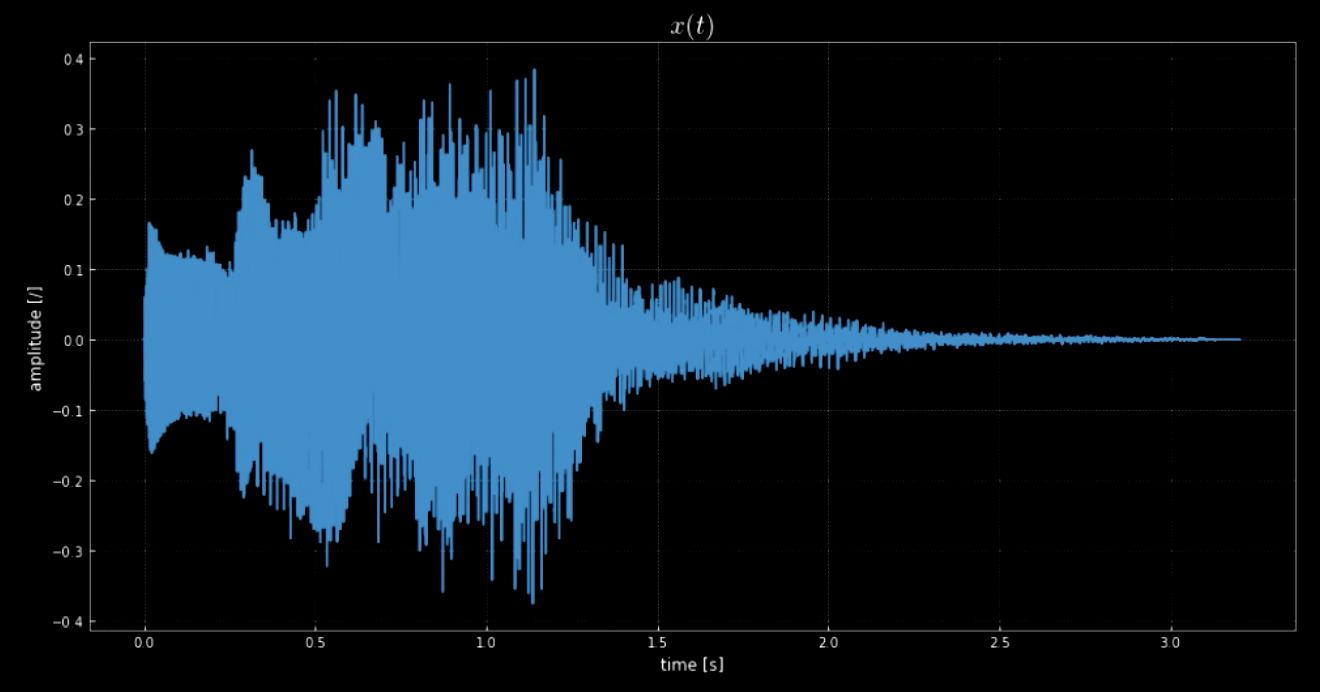
الشكل. 1: الإشارة الصوتية.

الشكل. 2: ملاحوظات للموجة الصوتية أعلاه.

في البداية نحتاج لعزل الدرجات الموسيقية عن بعضها في الموجة. إذا استعملنا تحويل فوريه (Fourier transform) سنحصل على كافة الدرجات وسيكون من الصعب تحديد زمن وموقع كل درجة. لذلك، سنستعمل تحويل فوريه على فترات قصيرة من الزمن (والذي يعرف بالمخطط الطيفي). كما نرى من المخطط الطيفي (انظر الشكل 3), تعلوا الدرجات المختلف عند ترددات مختلفة (على سبيل المثال الدرجة الأولى عند 1600). عند دمج الأربعة درجات، نستعيد المقطع الأصلي.

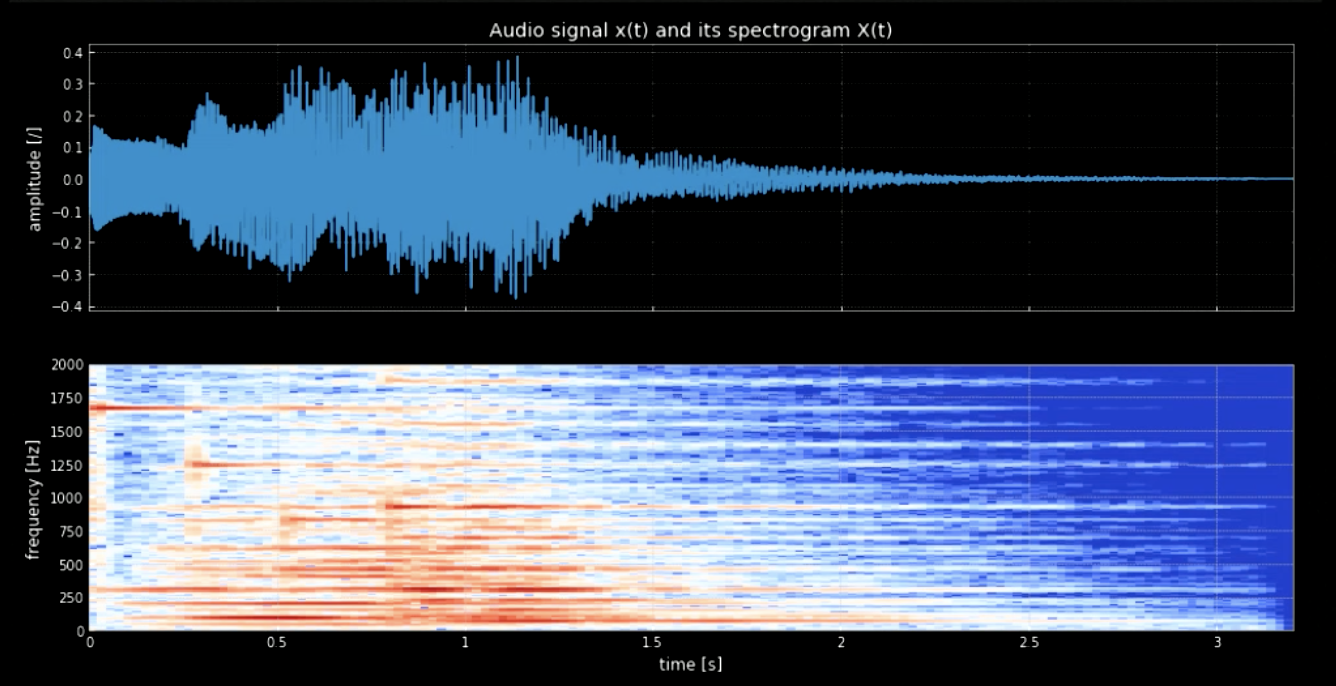
الشكل. 3: الإشارة الصوتية و مخطط طيفها.

يساعد التفاف الإشارة المدخلة مع كل الدرجات الموسيقية (مثلاً كل مفاتيح البيانو) على استخراج كل الدرجات من المقطع المدخل (أي عدنما يساوي التسجيل درجة مرشح ما). شكل 4 يوضح المخطط الطيفي للمقطع الأصلي وإلى جانبه المقطع المركب من الدرجات، في حين أن شكل 5 يوضح ترددات المقطع الأصلي والدرجات الأربع. أما شكل 6 فيوضح نتيجة التفاف المرشحات الأربعة مع المقطع الأصلي. يثبت الشكل 6 إضافة للمقاطع الصوتية للالتفاف يثبتان كفاءة الالتفاف في استخراج الدرجات الموسيقية.

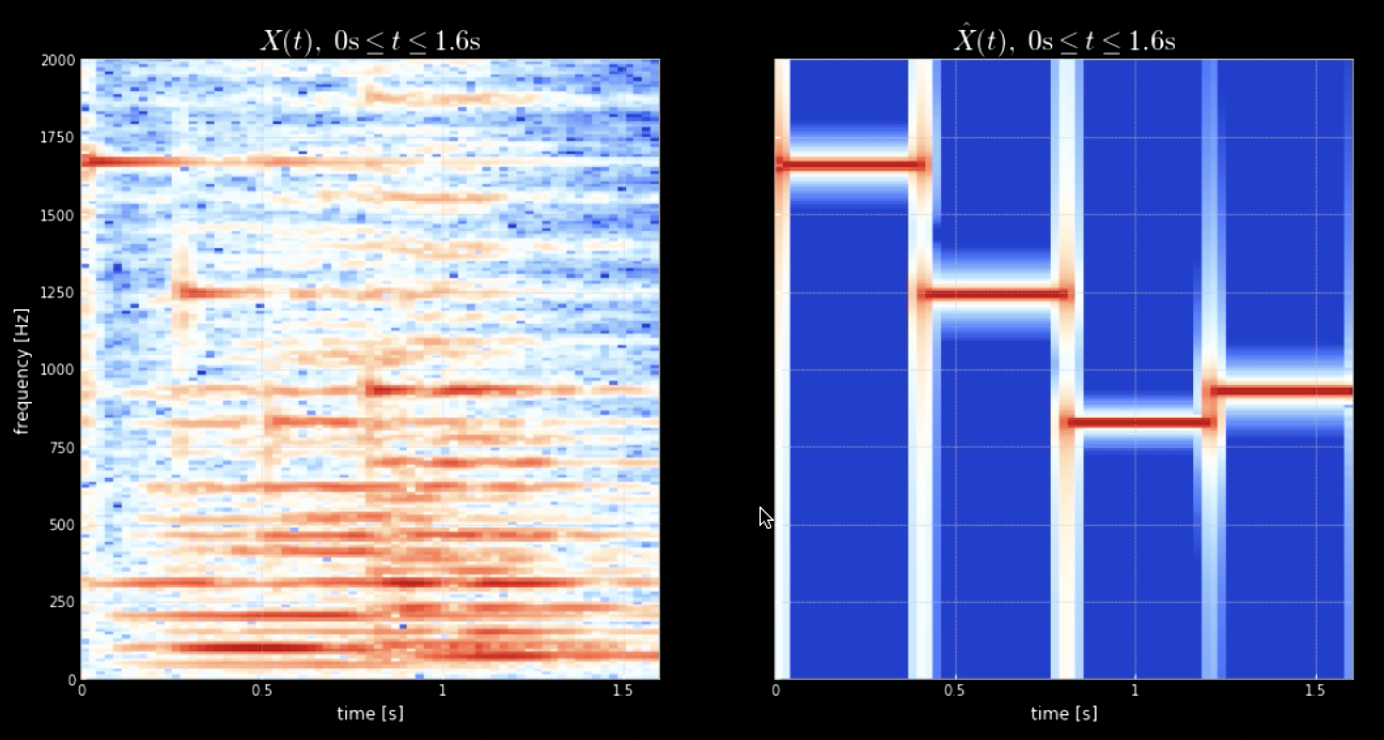
الشكل. 4: مخطط الطيف للإشارة الأساسية (يسار) و المخطط الطيفي لتركيز الدرجات الصوتية (يمين).

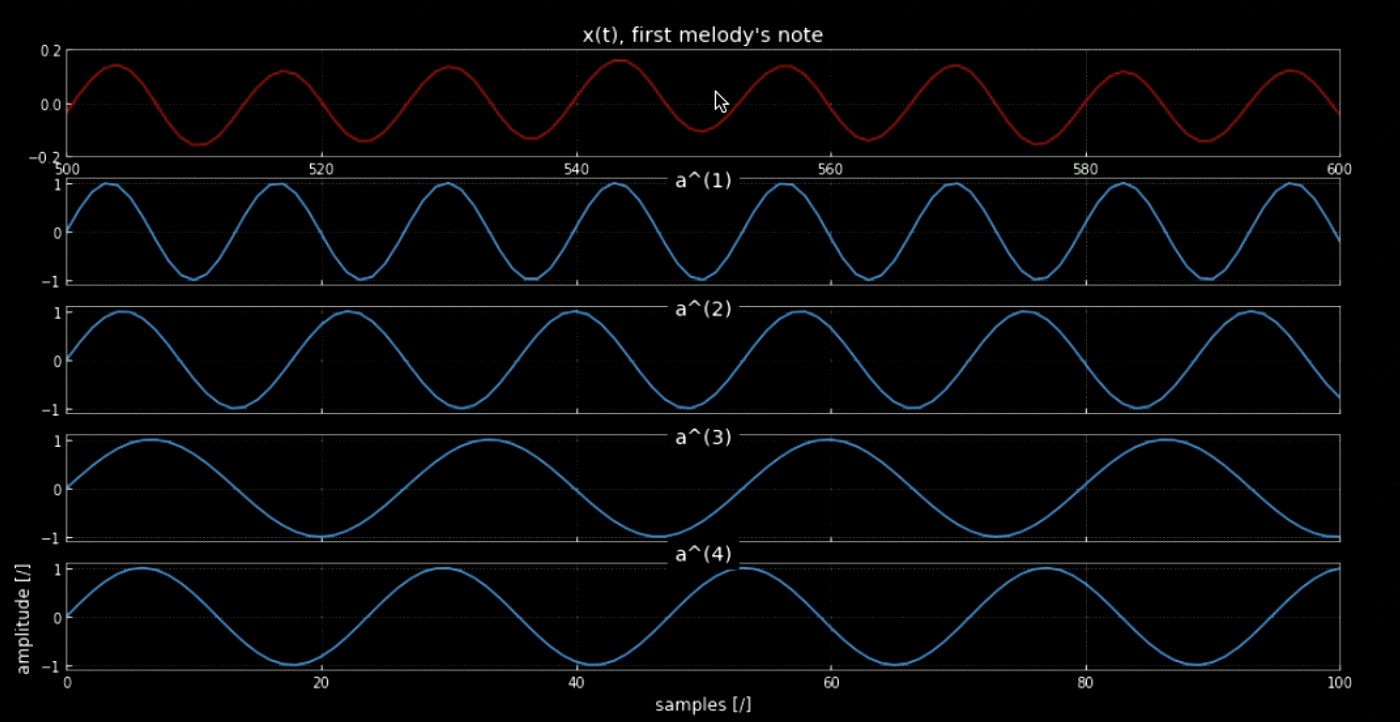
الشكل. 5: أول درجة موسيقية في المقطع.

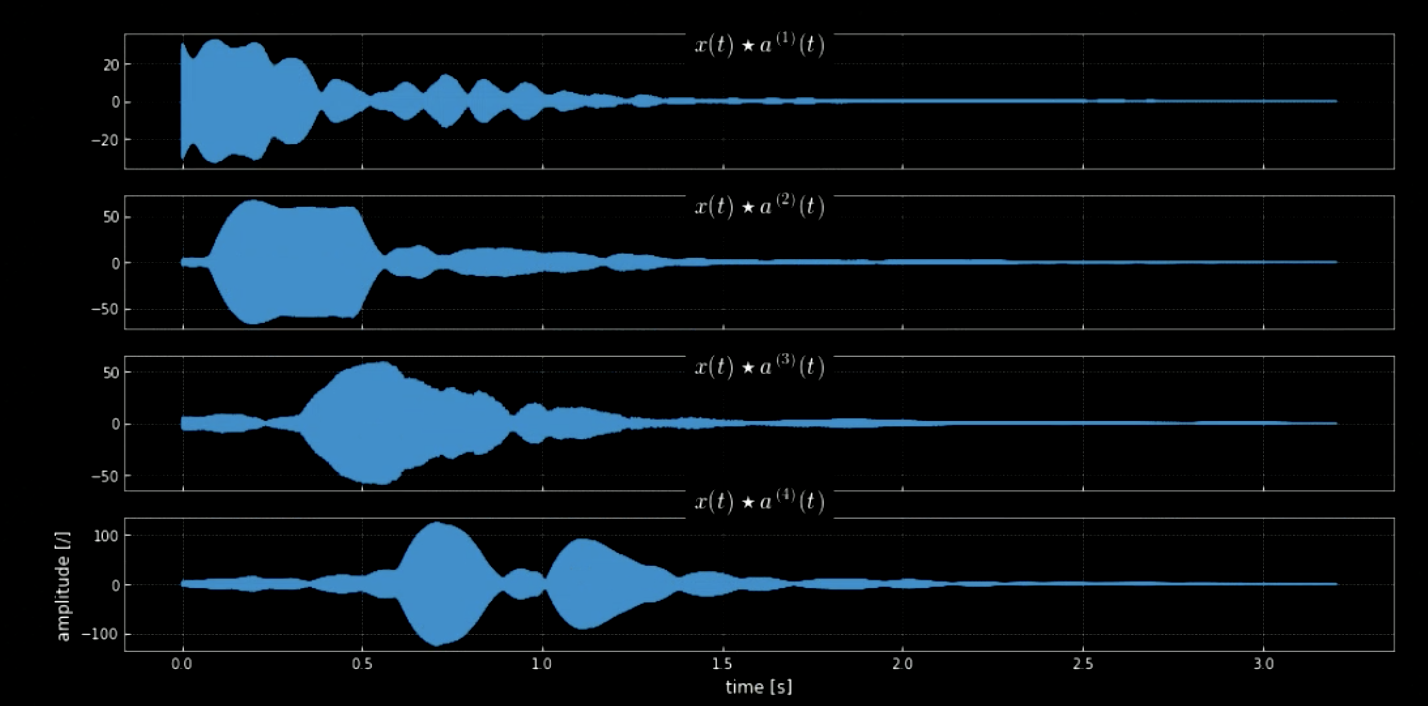
الشكل. 6: الالتفاف لأربعة مرشحات.

أبعاد البيانات المختلفة

في هذا الجزء، سنبتعد قليلاً عما سبق لنتحدث عن التمثيلات المختلفة للأبعاد مع أمثلة على ذلك. سنأخذ بعين الاعتبار المجال $X$ المعطى بالعلاقة من $\Omega$ إلى القنوات $c$.

أمثلة

• البيانات الصوتية: عناصر المجال أحادية البعد، إشارة رقمية متقطعة مجدولة بالزمن؛ عدد القنوات $c$ يتراوح بين 1 (أحادي)، 2 (ستريو)، 5+1 (دولبي 5.1) الخ
• الصور: عناصر المجال ثنائية الأبعاد (pixels)؛ $c$ يتراوح بين 1(تدرج رمادي)، 3(ملون)، 20(فائق الطيفية)، الخ
• النسبية الخاصة: المجال هو $\mathbb{R^4} \times \mathbb{R^4}$ (الزمكان $\times$ كميات الحركة الأربعة)؛ عند $c = 1$ المسمى بالهاملتوني (Hamiltonian)

الشكل. 7: الأبعاد المختلفة لأنواع مختلفة من الإشارات.

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
Ahmed Alhassan
18 Feb 2020