训练隐藏变量基础模型(EBM)
🎙️ Alfredo Canziani自由能
自由能:
\[F_\infty (\vect{y})=\min_z E(\vect{y},z) = E(\vect{y},\check z)\]在这里,$F_\infty$ 是零温度极限自由能,$\vect{y}$ 是2D向量。该自由能为距离模型流形的二次欧几里得距离,且模型流形内的所有点的能量均为零。当您将点远离流形时,它将以平方增长。
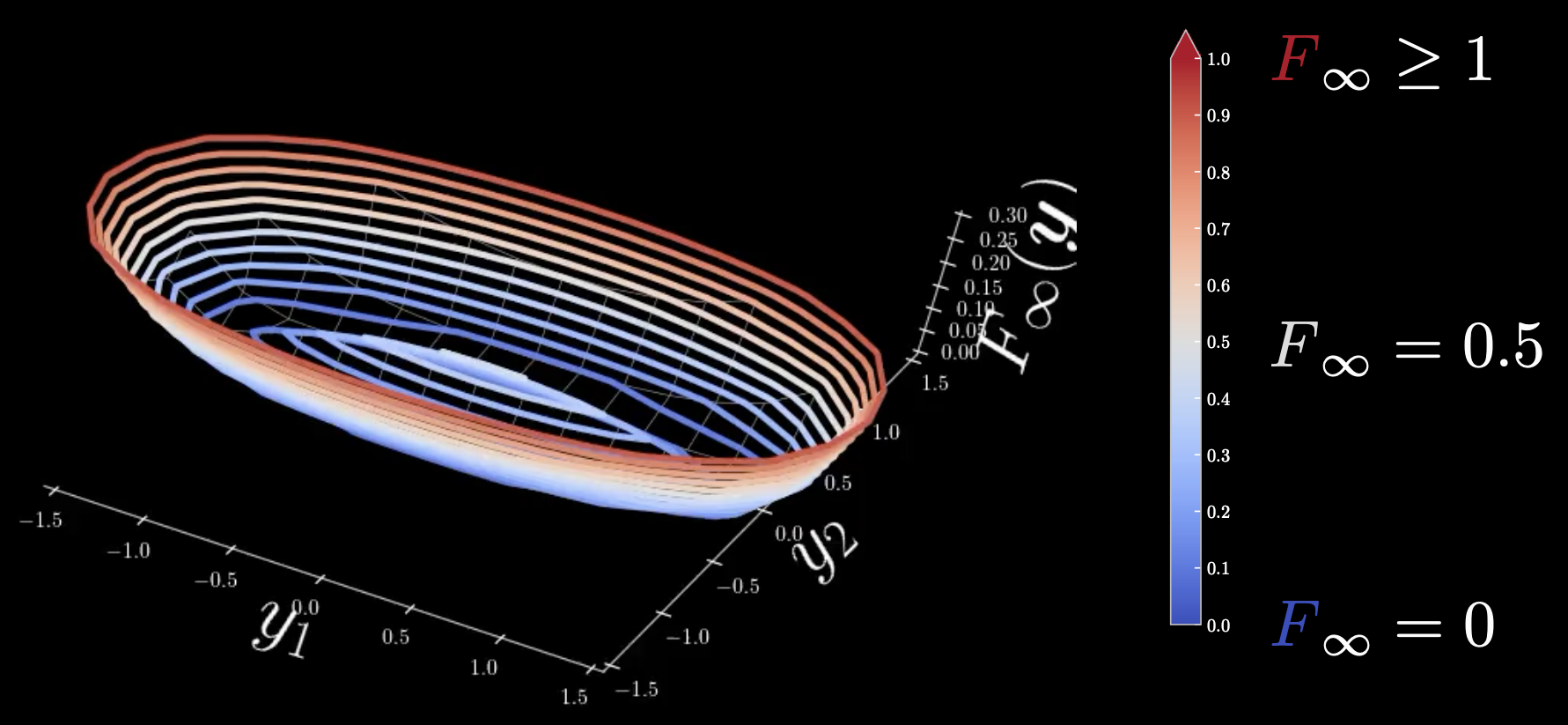
图 1: 冷暖色图
冷:$F_\infty = 0$, 暖:$F_\infty = 0.5$, 热:$F_\infty \geq 1$
椭圆周围在流形椭圆是的所有区域都将具有零能量,但是在中心处存在无限的零温度极限自由能。为了避免这种情况,我们需要将自由能放宽到没有局部最小值的状态,以使其变得更加平滑。
让我们用接下来的冷热图仔细看看在 $y_1=0$ 处的情况:
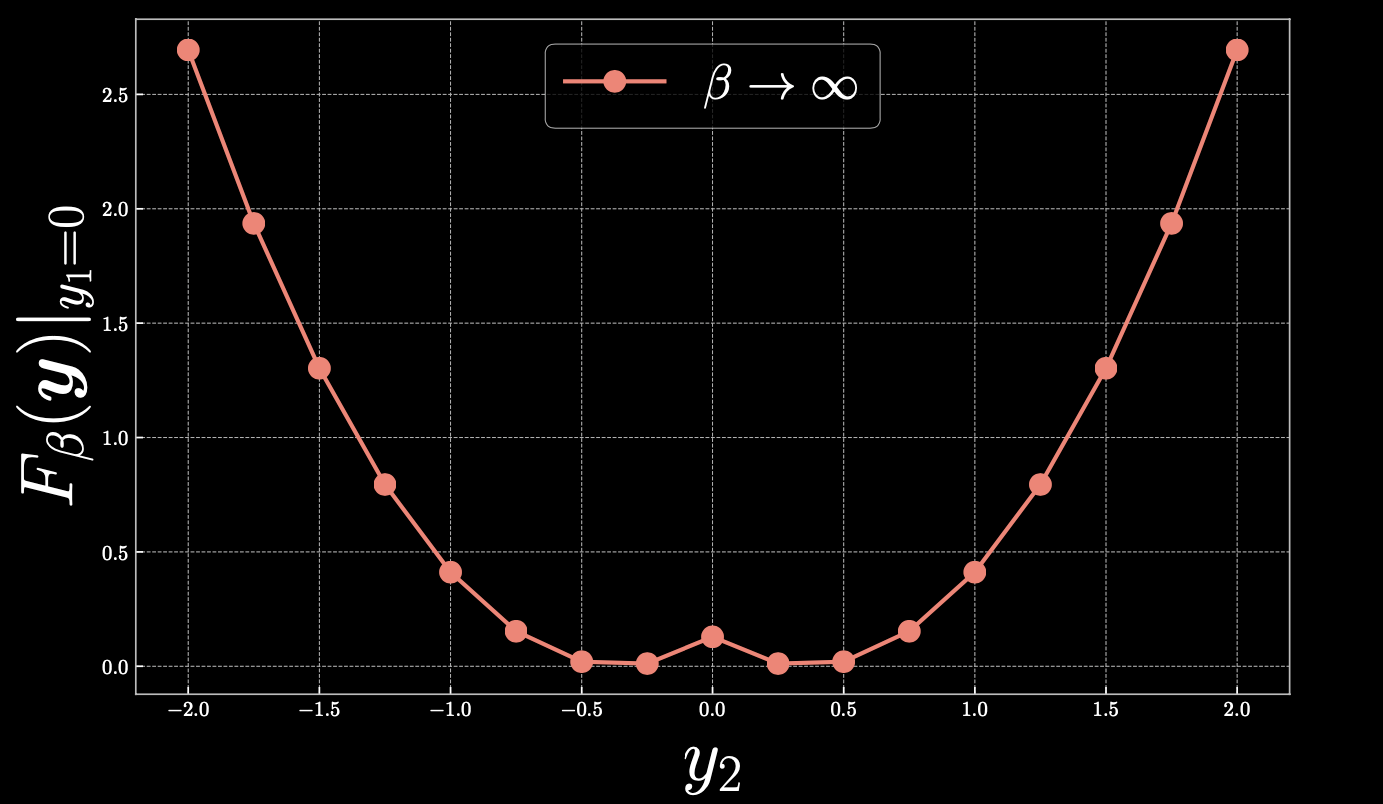
图 2
如果我们取 $y_2=0.4$, 那么 $F_\beta(\vect{y})=0$ 。当我们从该点向右侧线性移动时,自由能呈二次方增加。同样,如果我们向 $0$ 移动,你最终将沿着抛物线攀升,从而在中心形成一个峰值。
松弛版本的自由能
为了平滑我们先前观察到的峰值,我们需要放宽自由能函数:
\[F_\beta(\vect{y})\dot{=}-\frac{1}{\beta} \log \frac{1}{\vert\mathcal{Z}\vert}{\int}_\mathcal{Z} \exp[{-\beta}E(\vect{y},z)]\mathrm{d}z\]其中 $\beta=(k_B T)^{-1}$ 是逆温度,由玻尔兹曼常数乘以温度组成。如果温度很高 $\beta$ 将会非常小,如果温度很冷,那么 $\beta\rightarrow \infty$。
简单离散近似:
\[\tilde{F}_\beta(\vect{y})=-\frac{1}{\beta} \log \frac{1}{\vert\mathcal{Z}\vert}\underset{z\in\mathcal{Z}}{\sum} \exp[{-\beta}E(y,z)]\Delta z\]在这里,我们定义 $-\frac{1}{\beta} \log \frac{1}{\vert\mathcal{Z}\vert}\underset{z\in\mathcal{Z}}{\sum} \exp[{-\beta}E(\vect{y},z)]$ 为 $\smash{\underset{z}{\text{softmin}}}_\beta[E(\vect{y},z)]$, 从而使松弛版本的零温度极限自由能成为真正的 softmin。
例子:
现在,我们将回顾以前练习中的示例,并观察采用了松弛版本的效果。
情况 1: $\vect{y}’=Y[23]$
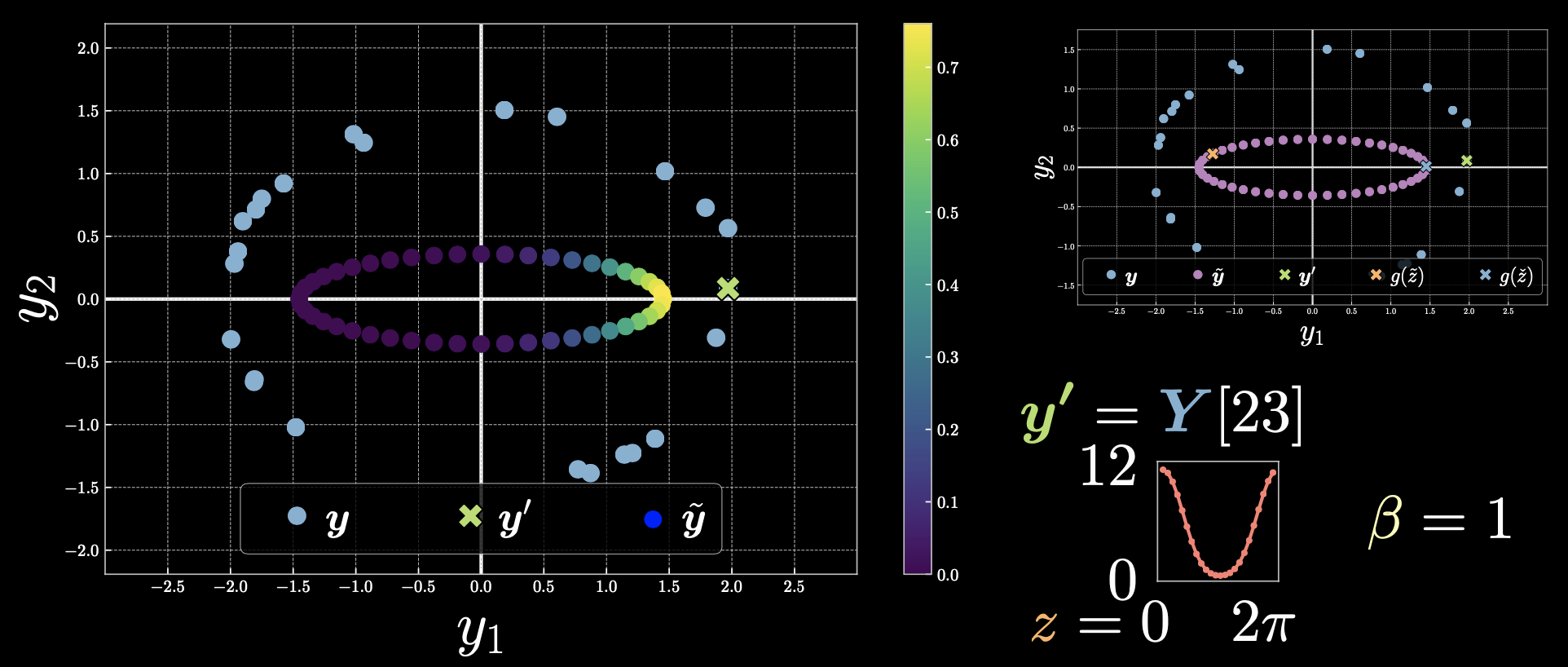
图 3
靠近点 $\vect{y}’$ 的点具有更小的能量,因此指数将较大,但对于距离较远的那些,指数将为零。
情况 2: $\vect{y}’=Y[10]$
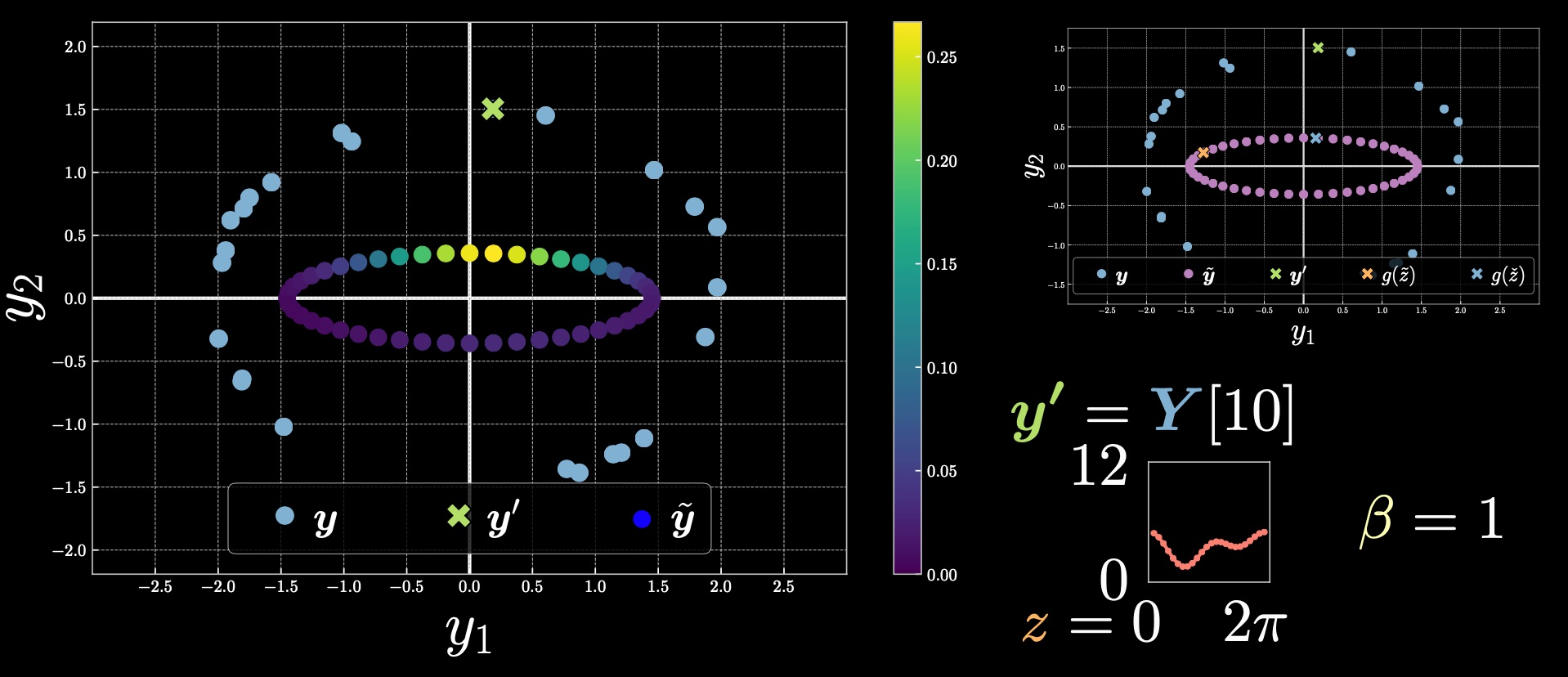
图 4
请注意颜色栏范围与上一个示例之间的变化。这里的上限值是从 $\exp[-\beta E(\vect{y},z)]$ 推导而来的。
情况 3: $\vect{y}’=(0,0)$
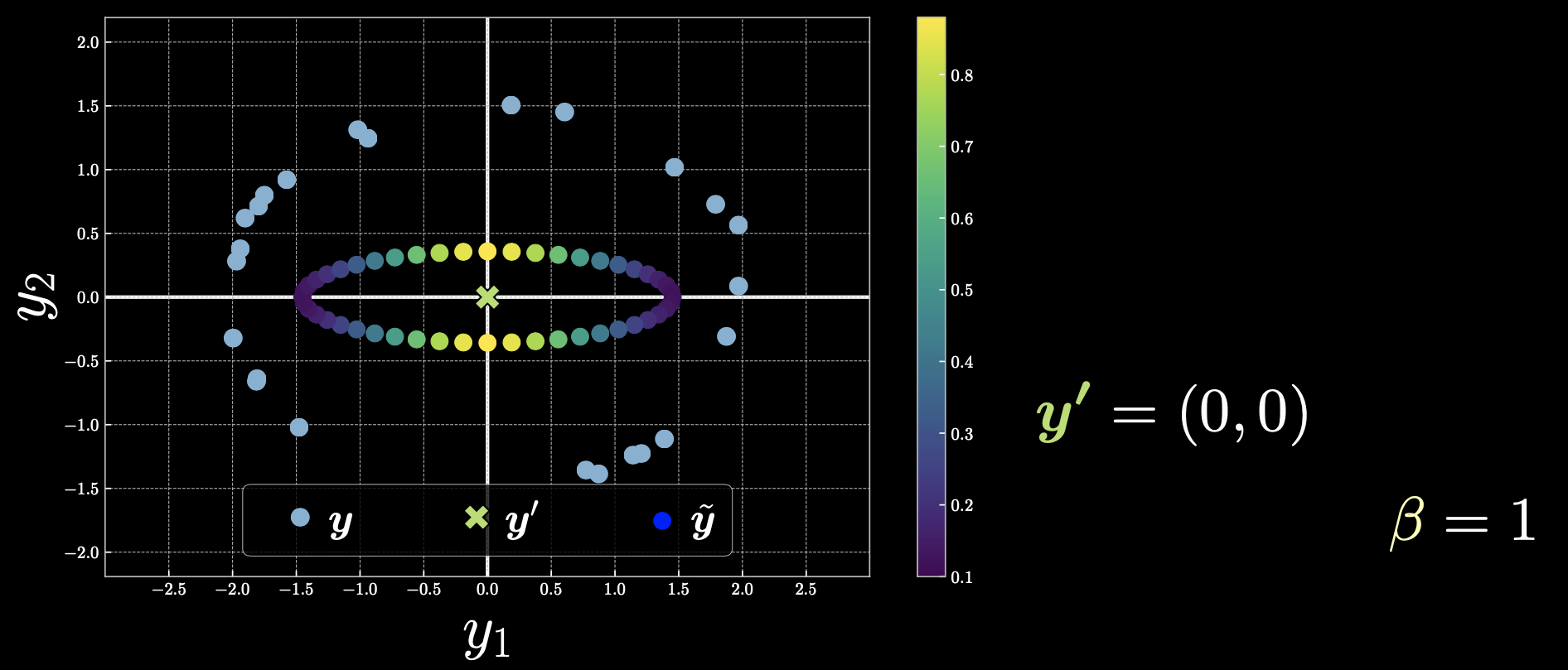
图 5
如果我们选择 $\vect{y}’$ 作为原点,那么所有的点都会起作用,自由能也会对称地变化。
现在,让我们回到如何平滑因冷能而形成的峰的问题上。如果我们选择了更暖一些的自由能,我们会得到如下描述。
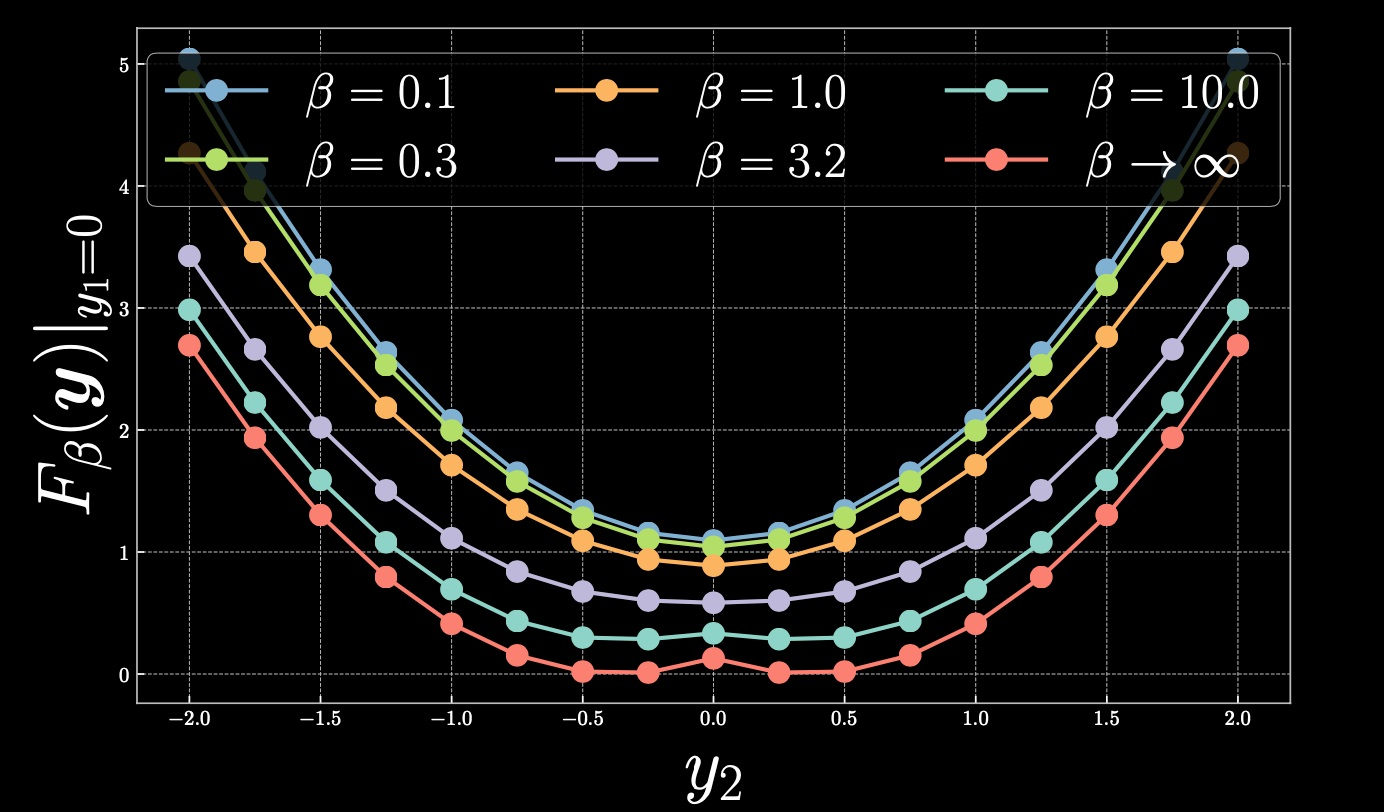
图 6
当我们通过降低温度 $\beta$ 来提高温度时,其结果为抛物线只有一个全局最小值。如 $\beta$ 接近0,你最终将得到平均值并恢复MSE。
命名方法和 PyTorch
正式地,我们将实际的 softmax 定义如下:
\[\smash{\underset{z}{\text{softmax}}}_\beta[E(y,z)] \doteq \frac{1}{\beta} \log \underset{z\in\mathcal{Z}}{\sum} \exp[{\beta}E(\vect{y},z)] - \frac{1}{\beta} \log{N_z}\]其中 $N_z = \vert\mathcal{Z}\vert / \Delta z$.
要在 PyTorch 中实现以上函数,可以如下所示使用 torch.logsumexp:
实际的 softmin:
\[\smash{\underset{z}{\text{softmin}}}_\beta[E(y,z)] \doteq -\frac{1}{\beta}\log\frac{1}{N_z}\underset{z\in\mathcal{Z}}{\sum}\exp[-{\beta}E(\vect{y},z)]\]可以使用带有2个负号的 softmax 来实现 softmin,如下所示:
\[\smash{\underset{z}{\text{softmin}}}_\beta[E(y,z)] = -\smash{\underset{z}{\text{softmax}}}_\beta[-E(y,z)]\] \[\texttt{torch.softmax}(l(j),\texttt{dim=j}) = \smash{\underset{j}{\text{softargmax}_{\beta=1}}}[l(j)]\]从技术的角度看待,如果自由能是
-
热的,它指平均值。
-
温的,它指隐变量的边缘化。
-
冷的,它指最小值。
训练 EBMs
目标——寻找良好表现的能量函数
在学习过程中最小化的损失函数被用于测量可用的能量函数的质量。简单来说,损失函数是一个标量函数,它告诉我们能量函数有多好。我们应当区分能量函数和损失函数(在第2节中介绍的),能量函数通过推理过程最小化,而损失函数通过学习过程最小化。
\[\mathcal{L}(F(\cdot),Y) = \frac{1}{N} \sum_{n=1}^{N} l(F(\cdot),\vect{y}^{(n)}) \in \R\]$\mathcal{L}$ 是整个数据集的损失函数,它可以被表示为每个样本的损失函数功能的平均值。
\[l_{\text{energy}}(F(\cdot),\check{\vect{y}}) = F(\check{\vect{y}})\]其中 $l_\text{energy}$ 是能量损失函数在数据集上的数据点 $\vect{y}$ 的值。$\check{\vect{y}}$ 标明了下一个要被往下推的数据点。这意味着在训练过程中损失函数会被最小化。
对于来自训练数据分布的数据,能量函数应该较小,而在其他地方则较大。
\[l_{\text{hinge}}(F(\cdot),\check{\vect{y}},\hat{\vect{y}}) = \big(m - [F(\hat{\vect{y}})-F(\check{\vect{y}})]\big)^{+}\]其中 $m$ 是边界,$F(\check{\vect{y}})$ 和 $F(\hat{\vect{y}})$ 是”冷“能量(对于正确标签)和”热“能量(对于错误标签)的自由能。
该模型试图使得两种能量的差值尽量大于边界 $m$。
我们注意到在ReLU function $[\cdot]^{+}$ 被应用于输出 $m - [F(\hat{\vect{y}}) - F(\check{\vect{y}})]$上。这意味着,Hingle 损失函数值将始终保持非负。这表明了,如果存在任何的负值,它们都会因为这个函数而变成 $0$。
训练将使得 $F(\hat{\vect{y}})-F(\check{\vect{y}})$ 等于或大于 $m$。如果差值变得大于 $m$,那么 $[m - [F(\hat{\vect{y}}) - F(\check{\vect{y}})]]$ 的最终结果将变负,Hinge 损失将变 $0$。我们也可以说,只要差值小于 $m$,我们就可以一直推动能量。然而,如果差值变得大于边界 $m$,我们需要停止推动能量。Hinge 损失函数并没有一个光滑的边界。
Log 损失函数有光滑的边界,如下所示。
\[l_{\log}(F(\cdot),\check{\vect{y}},\hat{\vect{y}}) = \log(1+\exp[F(\check{\vect{y}})-F(\hat{\vect{y}})])\]由于我们有指数函数,这种损失有更平滑的边界。换句话说,它们看起来像是具有无限边界的”柔软“版本的 Hinge 损失。
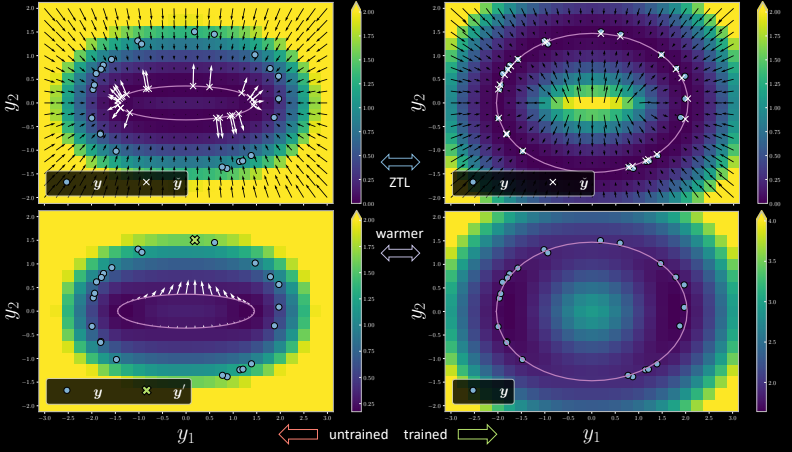
图 7
左侧是未经训练的版本,其中每个训练数据点都有一个对应的 $x$,如图中所示,它是模型流形上最靠近训练数据点的位置。在以ZTL(零温度极限)进行训练期间,梯度会使最接近训练数据点的流形上的数据点被推向训练数据点。
我们可以看到,在右侧图像上经过一次迭代之后,训练后的模型版本显示 $x$ 个点到达了所需位置,并且能量变为与训练点相对应的零(图中的蓝色点)。
现在让我们谈谈边缘化。当在ZTL训练模型并温度被提高时,数据点被分别推向训练数据点。但是,在边缘化的情况下,如果我们选择一个点 $\vect{y}$ (左下方图像上的绿色十字点),梯度只是指向该特定点的所有箭头的平均值 $\vect{y}$。这使得所有要点都趋向于 $\vect{y}$,以确保它不会过拟合训练数据。请注意受训版本有多不适合所有的训练数据点。
现在让我们在以下图表中查看训练版本的横截面。对于ZTL(${\beta = {\infty}}$),我们可以看到自由能具有很高的峰值。随着我们减少 ${\beta}$,尖峰会不断减小,我们持续减少它,直到我们获得蓝色的平滑抛物线图(这是边缘化情况下的图)。
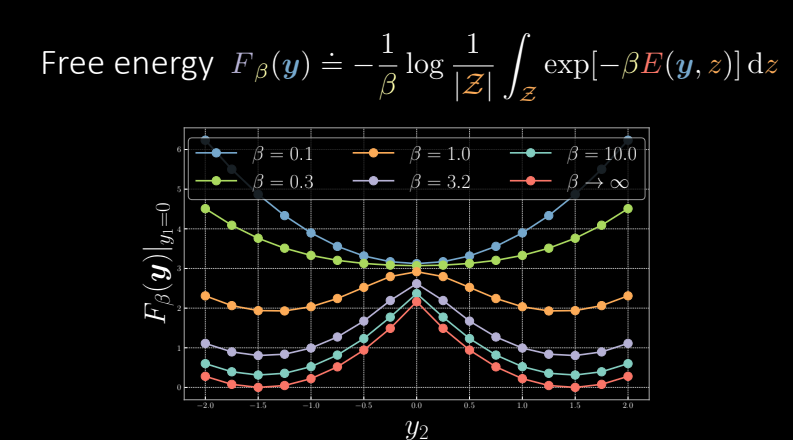
图 8 自由能量
现在让我们继续进入下一环节:自监督学习(有条件的情况)。
自监督学习
回顾训练数据:
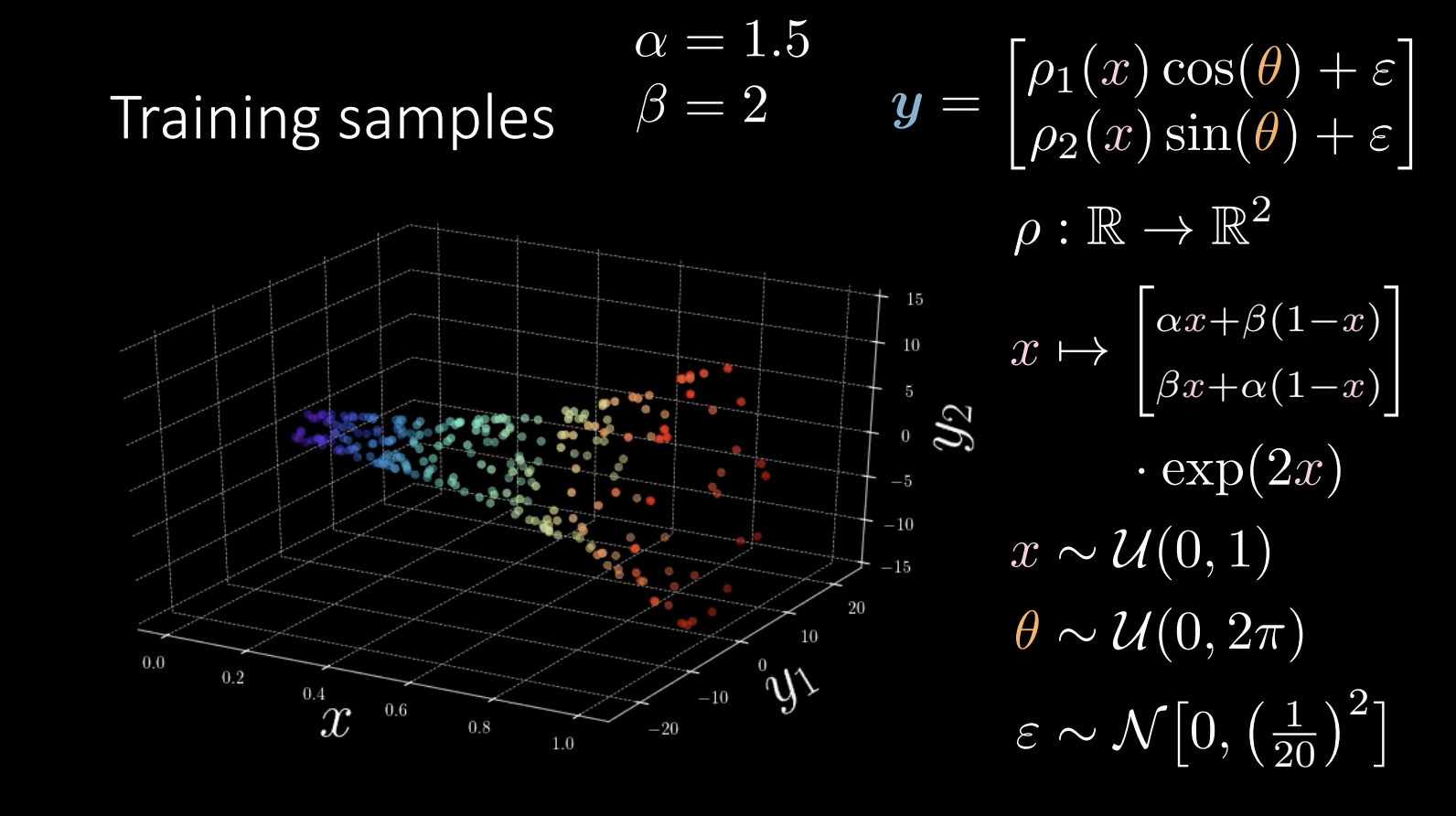
图 9
在训练过程中,我们尝试学到”号角“的形状。
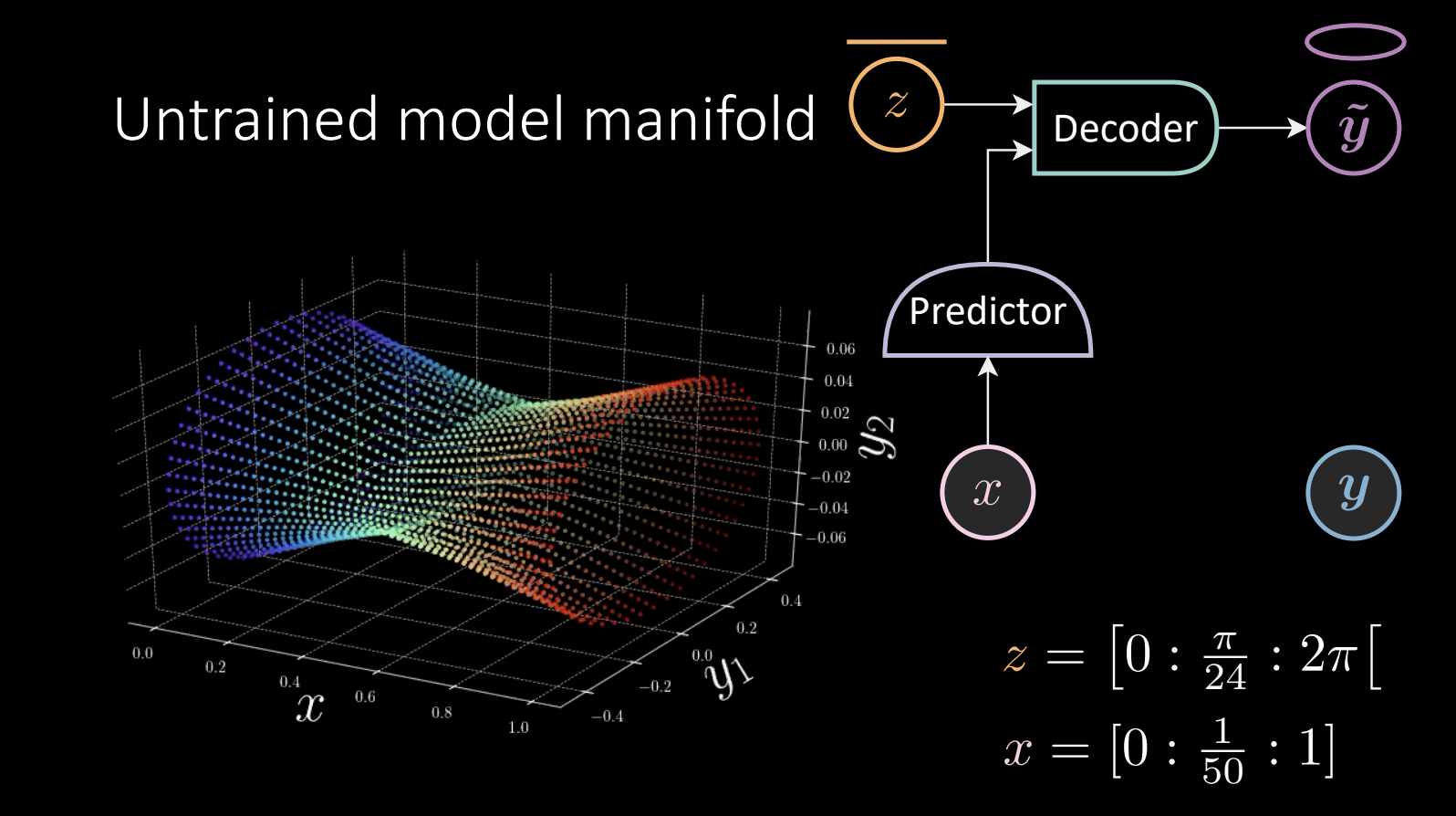
图 10 未训练的模型流形
$z$ 线性取值,并被送入解码器得到 $\tilde{\vect{y}}$,得到的 $\tilde{\vect{y}}$ 会环绕椭圆。
\[x = [0:\frac{1}{50} :1]\]预测器获得观测到的 $x$, 并将结果送入解码器。
我们执行温度自由能训练,其结果为:
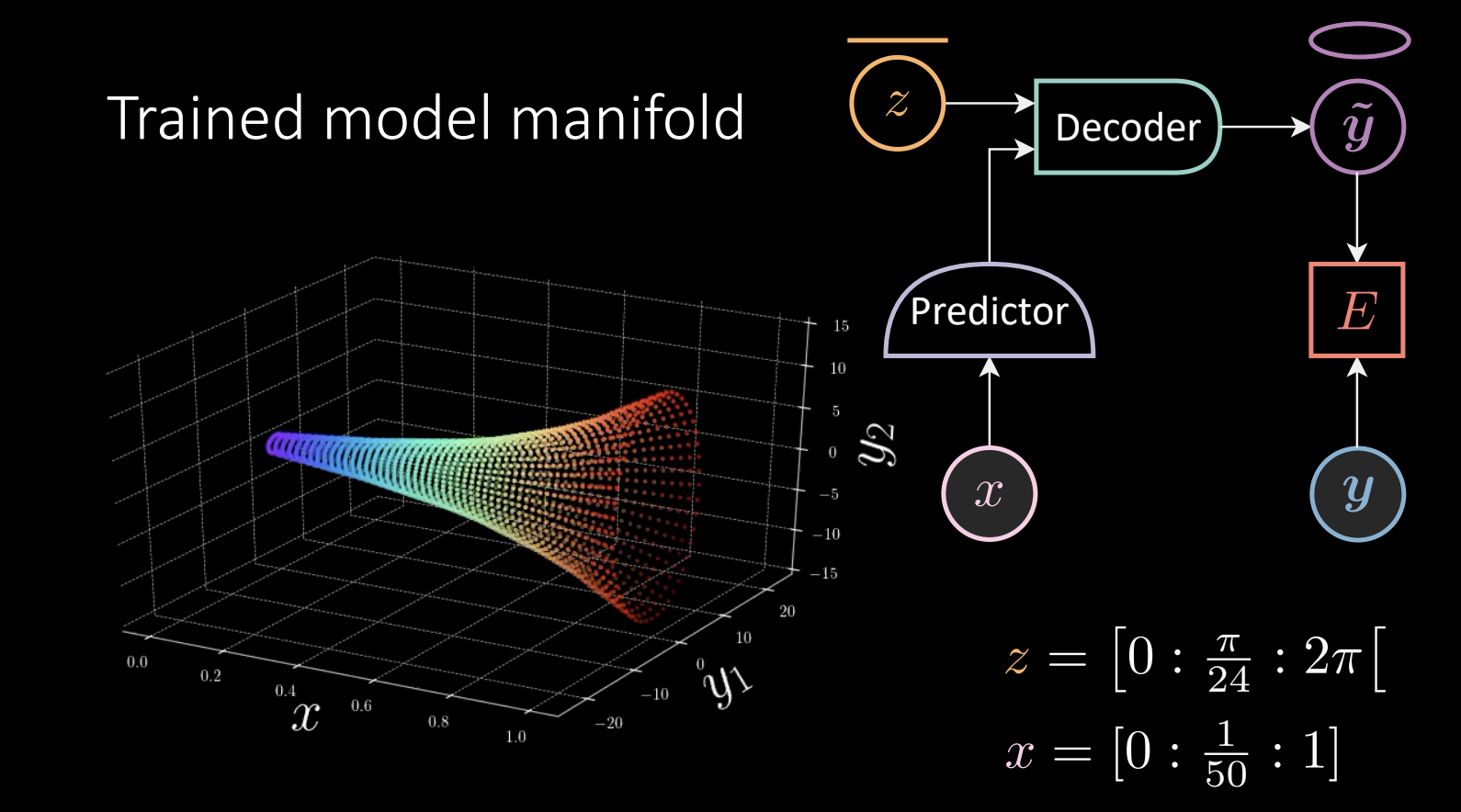
图 10 未训练的模型流形
对于给定的”号角“,我们选择一个数据点 $\vect{y}$, 找到流形上离它最近的点,并将其拉向 $\vect{y}$。
在这种情况下,能量函数被定义为
\[E(x,\vect{y},z) = [\vect{y}_{1} - f_{1}(x)g_{1}(z)]^{2} + [\vect{y}_{2} -f_{2}(x)g_{2}(z)]^{2}\]其中
\[f,g:\mathbb{R} \rightarrow \mathbb{R}^{2}\] \[\begin{array}{l} x \stackrel{f}{\mapsto} x \stackrel{\mathrm{L}^{+}}{\rightarrow} 8 \stackrel{\mathrm{L}^{+}}{\rightarrow} 8 \stackrel{\mathrm{L}}{\rightarrow} 2 \\ z \stackrel{g}{\mapsto}[\cos (z) \quad \sin (z)]^{\top} \end{array}\]$g$ 的部分被 $f$ 的输出缩放。
示例数据不需要花费时间训练。但我们应该如何推广它呢? \(\begin{array}{l} f: \mathbb{R} \rightarrow \mathbb{R}^{\operatorname{dim}(f)} \\ g: \mathbb{R}^{\operatorname{dim}(f)} \times \mathbb{R} \rightarrow \mathbb{R}^{2} \end{array} \\ E(x, \vect{y}, z)=\left[\vect{y}_{1}-g_{1}(f(x), z)\right]^{2}+\left[\vect{y}_{2}-g_{2}(f(x), z)\right]^{2}\)
在这个例子中,$g$ 函数获得 $f$ 和 $z$,而且 $g$ 可以使一个神经网络。这次,该模型需要学习 $\vect{y}$ 绕圈移动,也就是我们之前认为理所当然的 $\sin$ 和 $\cos$ 部分。
另一个问题是需要确定隐变量 $z$ 的维度。 \(\begin{array}{l} f: \mathbb{R} \rightarrow \mathbb{R}^{\operatorname{dim}(f)} \\ g: \mathbb{R}^{\operatorname{dim}(f)} \times \mathbb{R}^{\operatorname{dim}(z)} \rightarrow \mathbb{R}^{2} \end{array}\\ E(x, \vect{y}, z)=\left[\vect{y}_{1}-g_{1}(f(x), z)\right]^{2}+\left[\vect{y}_{2}-g_{2}(f(x), z)\right]^{2}\)
因为高维隐变量倾向于过拟合。我们需要正则化 $z$。否则,模型将会记住所有数据点,从而导致整个空间的能量为零。
📝 Anu-Ujin Gerelt-Od, Sunidhi Gupta, Bichen Kou, Binfeng Xu
Yang Zhou
31 Oct 2020