隐变量能量模型（EBM）的推导

训练数据和模型定义

为了理解为什么以及如何使用能量基础模型（EBMS），以及相关的数据格式，让我们从一个椭圆开始考虑训练样本。我们在下面给出方程。 \(\vect{y} = \begin{bmatrix} \rho_1(x)\cos(\theta) + \epsilon \\ \rho_2(x)\sin(\theta) + \epsilon \end{bmatrix},\)

其中 $x \sim \mathcal{U}(0,1),\space \theta \sim \mathcal{U}(0,2\pi),\space \epsilon \sim \mathcal{N}[0, (\frac{1}{20})^2]$ 而且 $\rho : \mathbb{R} \mapsto \mathbb{R}^2$ 将 $x$ 映射到 \(\begin{bmatrix}\alpha x + \beta (1-x) \\ \beta x + \alpha (1-x) \end{bmatrix}\exp(2x)\)。

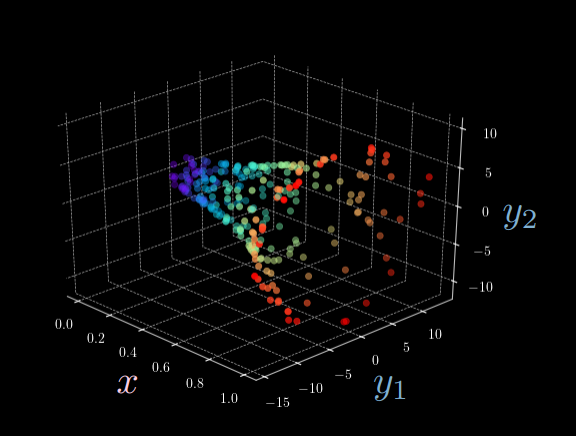
图 1: 椭圆函数的3D可视化

从图1中，我们可以清楚地看到，给定一个单独的输入 $x$, 存在多一个可能的输出 $\vect{y}$。换一句话说，我们无法想我们期待的那样通过前向神经网络分辨出一对一映射。（例如，对于指定的输入 $x$，总会存在两个不同的 $y_2$ 将 $y_1$ 固定住）。正因如此，我们需要引入隐变量能量基础模型。

为了简化，我们将输入 $x=0$ 固定，并令 $\alpha = 1.5, \beta = 2$， 从而得到 \(\vect{y} = \begin{bmatrix} 2\cos(\theta) + \epsilon \\ 1.5\sin(\theta) + \epsilon \end{bmatrix}\) 。从中，我们随机采样 $24$ 个数据点 $Y = [\vect{y}^{(1)},\ldots,\vect{y}^{(24)}]$ 。同时，我们取隐变量 $z = [0:\frac{\pi}{24}:2\pi)$ 并将其送入一个解码器得到 $\tilde{\vect{y}}$ （图2和图3）。然后，我们用 $\vect{y}$ 和 $\tilde{\vect{y}}$ 之间的欧几里得距离计算能量函数。 \(E(\vect{y},z) \equiv E(\vect{y},\tilde{\vect{y}}(z)) = [y_1 - g_1(z)]^2 + [y_2 - g_2(z)]^2, \space \vect{y} \in Y,\)

其中 $\vect{g} = [g_1 \space\space g_2]^{\top} : \mathbb{R} \mapsto \mathbb{R}^2$ ， $\vect{g}(z) = \ [w_1 \cos(z) \space\space w_2 \sin(z)]^{\top}$

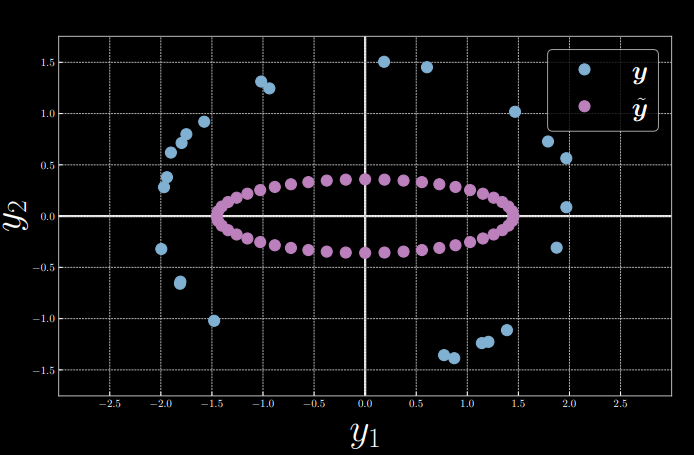
图 2: 采样样本可视化

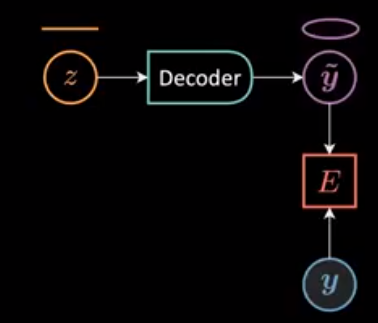
图 3: 能量计算图

对于 $\vect{y}^{(i)} \in Y, i \in [1,24]$， 我们可以在给定每个 $\tilde{\vect{y}}$ 的情况下，通过改变 $z$ 来计算相对应的能量。从而，我们可以可视化 $24$ 个能量函数 $E_{1},\ldots,E_{24}$ 。其中，y轴上的能量值是根据位于x轴上隐变量 $z$ 的选择绘制的。

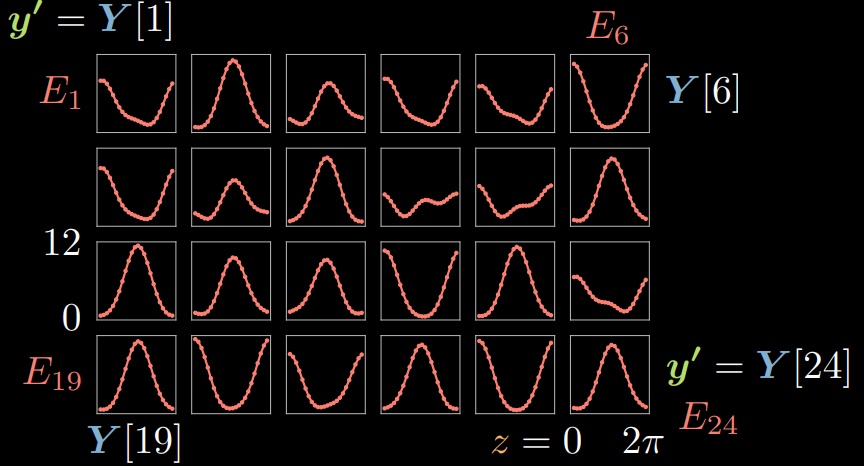
图 4: 不同样本上的能量函数

两个训练样本下的能量和自由能

让我们继续深入给定 $\vect{y}^{(i)}$ 时 $E(\vect{y}, z)$ 的函数形式。图 5 展示了 $E(\vect{y}^{(23)}, z) = E_{23}$ 的图形。

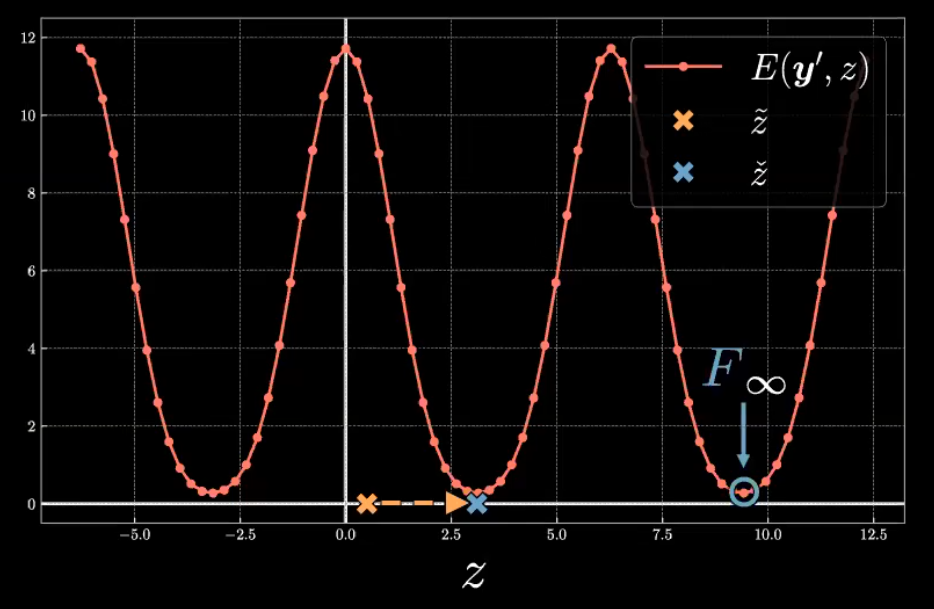
图 5: 第23个样本的能量函数

能量函数 $E_{23}$ 是一个周期函数，其中最大值在 $z=0$ 和 $2{\pi}$ 附近，最小值在 $z={\pi}$ 附近。该能量函数的对称形状是由于 $\vect{y}^{(23)}$ 在 $\vect{y}$ 空间中相对于 解码后 $\tilde{\vect{y}}$ 的位置引起的。

正如图6所示，用绿色点表示的$\vect{y}^{(23)}$ 十分靠近用紫色点表示的 $\tilde{\vect{y}}$ 水平轴，其中 $\tilde{\vect{y}}$ 在 $E_{23}$ 形成了对称形状。隐变量 $z$ 可以被看作一个以顺时针为正方向的反向极坐标角。在 $z=0$ （最左边的紫色点），$\tilde{\vect{y}}$ 和 $\vect{y}^{(23)}$ 间的欧几里得距离在很大程度上引起了很高的能量。当 $z$ 靠近 ${\pi}$ （最右边的紫色点），$\tilde{\vect{y}}$ 更靠近 $\vect{y}^{(23)}$ ，从而导致能量减少到一个最小值。相反的，当 $z$ 超过 ${\pi}$ 向 $2{\pi}$ 增长时，$\tilde{\vect{y}}$ 和 $\vect{y}^{(23)}$ 的距离增加，并且能量增长到一个最大值。

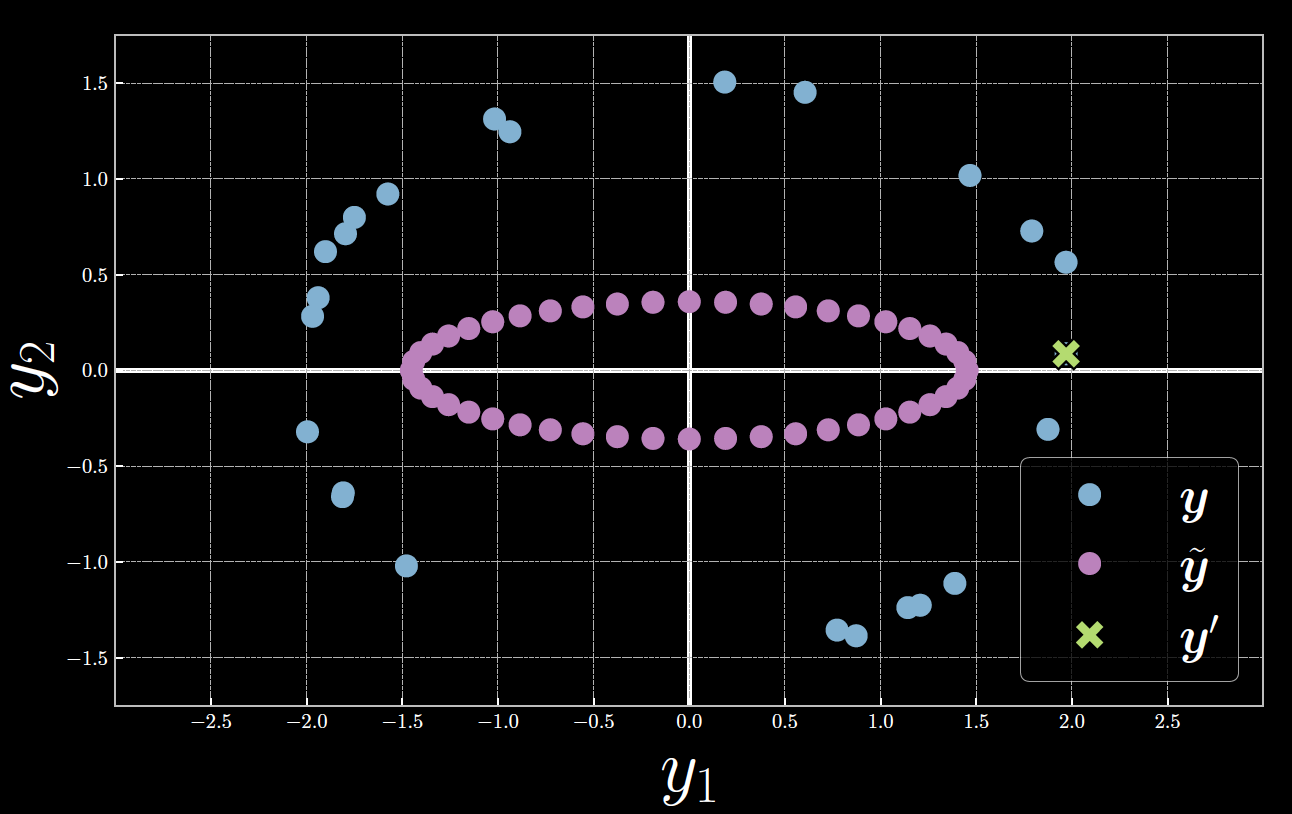
图 6: 隐变量，解码器输出和第23个样本间的关系

现在我们有了一个关于能量分布的理解，现在让我们来计算如下定义的自由能的零温度极限。

同时，我们也将表示产生了如下定义的自由能 $\check{z}$ 的隐变量。

如图5所示，为了找到与 $\vect{y}^{(23)}$ 相关联的自由能，我们会从初始隐变量 $\tilde{z}$ 开始。$\check{z}$ 可以通过如穷举搜索，共轭梯度，线搜索或有限内存BGFS的优化算法进行计算。自由能便是相对于隐变量的能量的最小值。

下图图7展示了在 $\vect{y}$ 空间自由能的计算结果。注意，隐变量在优化的过程中的增长导致了 $\tilde{\vect{y}}$ 朝向 $\vect{y}^{(23)}$ 顺时针移动。在自由能处，能量是最小的，从而 $\tilde{\vect{y}}$ 和 $\vect{y}^{(23)}$ 间的距离也是最小的。

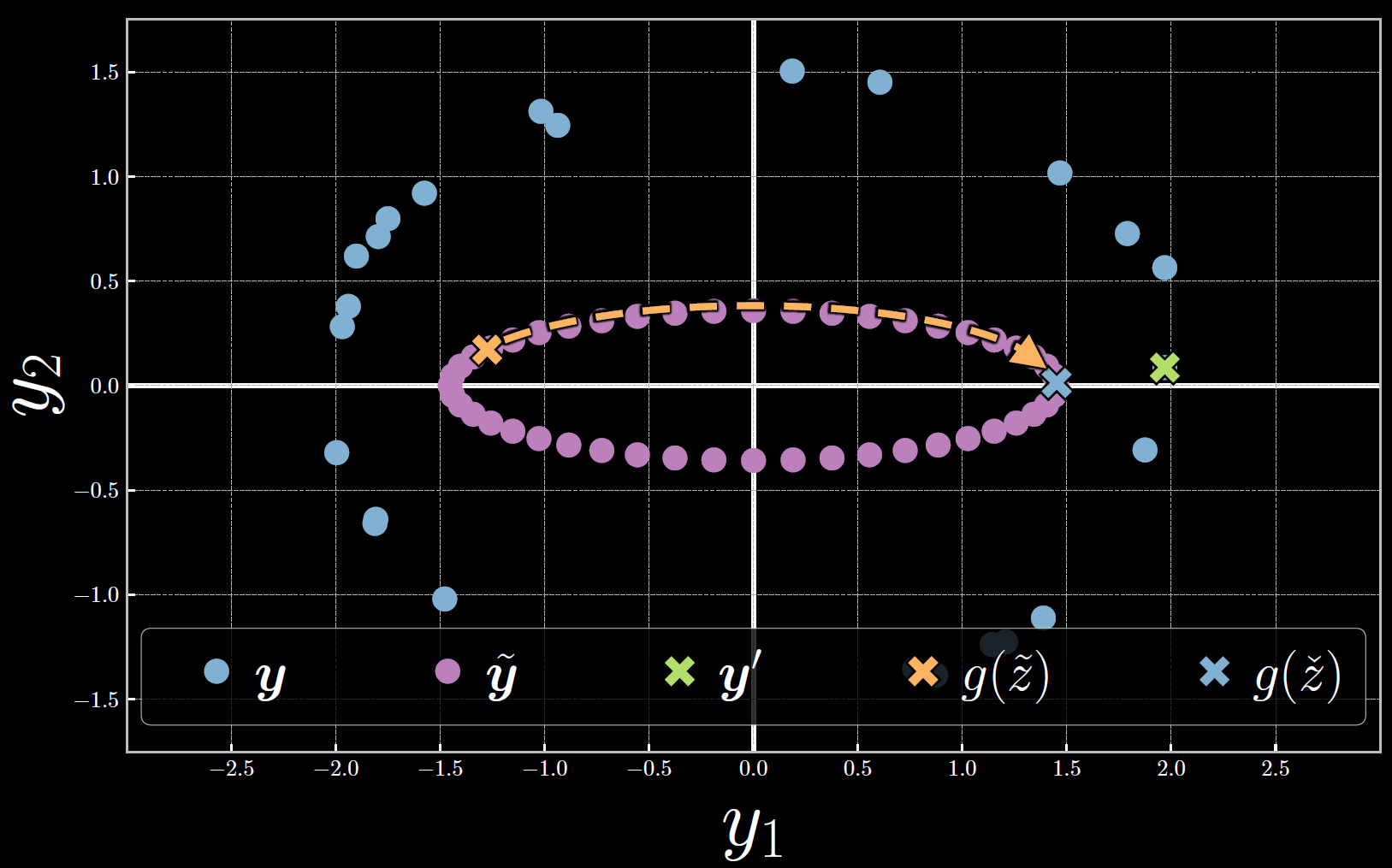
图 7: 第23个样本相关联的自由能计算结果

在计算自由能 $F_\infty$ 和其相关的隐变量 $\check{z}$ 的过程中，我们能找到靠近样本数据 $\vect{y}^{(i)}$ 的解码结果 $\tilde{\vect{y}}$ 。

Free energy dense estimation

为了能更好的理解自由能函数，我们从如下图8所示的例子开始。

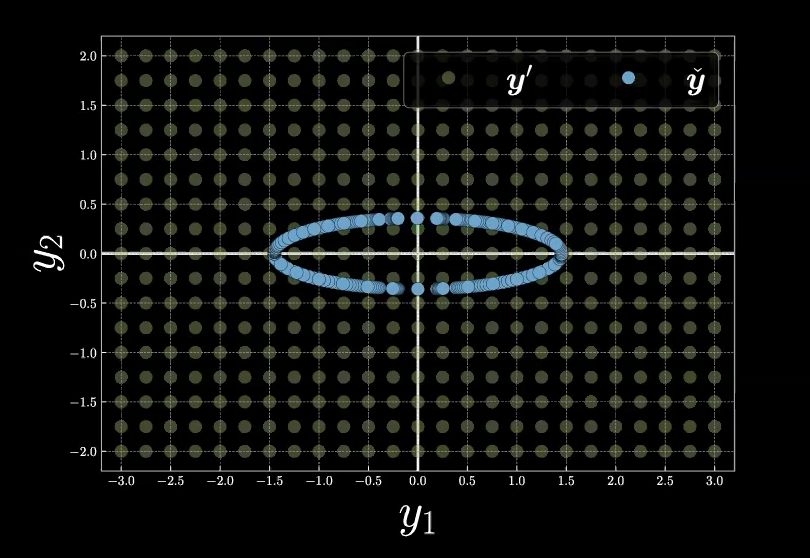
图 8: 网格中的自由能示例

为了计算相对于用蓝色表示的流形（同时也是隐变量 $z$ 的所有选择）的每个网格格点上的自由能 $F_\infty$。我们首先在下面回顾自由能函数的定义。 \(F_\infty = \min_z E(\vect{y},z) = E(\vect{y},\check{z}).\)

在给出能量函数公式，$E(\vect{y},z)$，和（样本）位置 $\vect{y}$，我们的最小化优化过程从推理阶段开始，这也正是找到最有可能生成样本位置的隐变量 $\check{z}$ 的过程。从图8的图像上，我们可以从蓝色流形的任意一点 $z$ 开始在流形上移动，以寻找流形上离我们的采样位置 $\vect{y}$ 距离最近的点 $\check{z}$。最终，自由能便是我们的采样位置 $\vect{y}$ 和所选点 $\tilde{\vect{y}}(\check{z})$ 间的欧几里得距离。

现在，如图9所示，我们考虑网格格点中的5个颜色不同的特定采样点。

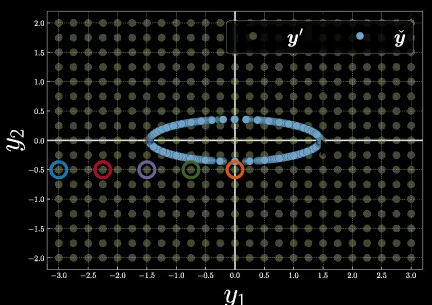
图 9: 网格上的五个采样点

利用我们上面学到的知识，我们可以针对流形上隐变量 $z$ 的不同选择，对这五个点的能量函数的形状进行猜测。确切地说，蓝色点可能具有很大幅度的能量函数值，也便是这五个点中最大的自由能。而橙色点可能有最小的自由能。

在图10中，我们给出了五个能量函数的完整图形。X符号代表了每个能量函数的 $\check{z}$ 值。

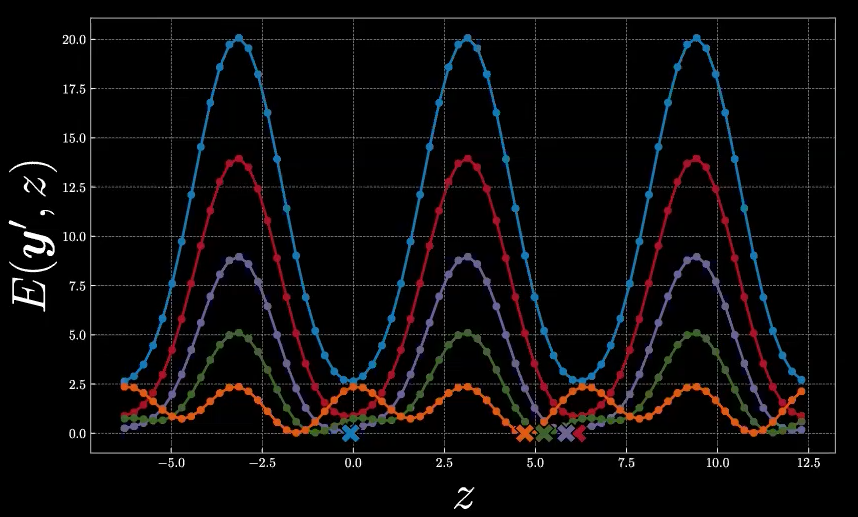
图 10: 五个点的能量函数

我们继续上述例子，可以主要到，我们的自由能函数 $F_\infty$ 在它的范围内只有非负标量值（因为我们使用 $E(\vect{y},z)$ 的欧几里得距离），而我们的自由能函数 $F_\infty$ 的定义域是 $\mathbb{R}^2$ （只是 $\vect{y}$ 的空间），所有我们有 $F_\infty :\mathbb{R}^2 \rightarrow \mathbb{R}^+$ 。我们现在用自由能值作为我们的推论，将上述网格绘制成如下图11所示的热力图。注意，箭头代表梯度值。

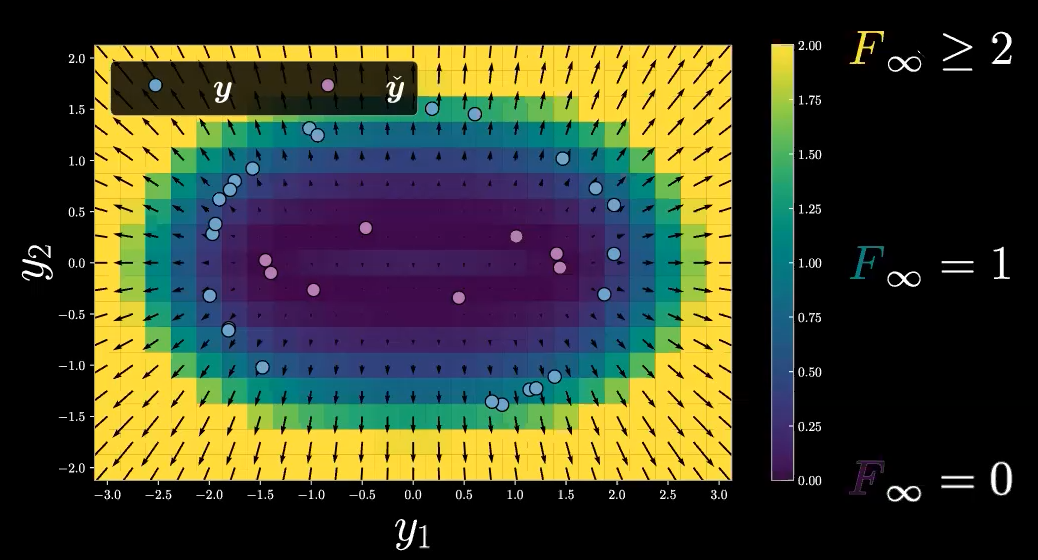
图 11: Free Energy Heat Map

综上所述，我们在这里仅仅讨论了自由能的一个简单示例。在实际情况中，我们会有更广泛的隐变量 $z$ 的选择，而不想我们的椭圆流形例子中的唯一选择。然而，我们需要记住，自由能值 $F_\infty$ 完全不依赖与隐变量。

理解性问答

问题1：为什么能量平面上的值是标量？

能量平面上的值是自由能值 $F_\infty$，也恰恰是我们的能量函数 $E(\vect{y},z)$ 对于所有可能的隐变量 $z$ 的最小值。所以 $F_\infty$ 不依赖于 $z$， 只依赖于 $\vect{y}$，并对 $\vect{y}$ 的每个选择都输出一个标量值。

、

考虑到上述的网格示例，网格上有 $17\times 25 = 425$ 个点，所以我们会有 425 个自由能值，每个值都是每个点到流形的二次欧几里得距离。

问题2：如何选择表达数据流形的函数？

关于隐变量选择的研究有很多，我们可以用几层神经网络来表达选择的隐变量。

一个典型的例子是语言翻译。我们可以以不同的方式翻译句子，我们不会在魔性训练中使用 softmax 函数，因为那样的话，翻译后将可能会有无穷可能的句子结果。因此，我们在这里使用 EBM，并且能量函数将会告诉我们原始句子和翻译后句子的匹配性。

问题3： 将经过训练的流形上的能量最小化基本上意味着去噪吗？

如果模型是从真实的流形中学到的，那么你可以通过最小化能量来找到你的输入的去噪版本。