图能量模型
🎙️ Yann LeCun损失函数对比
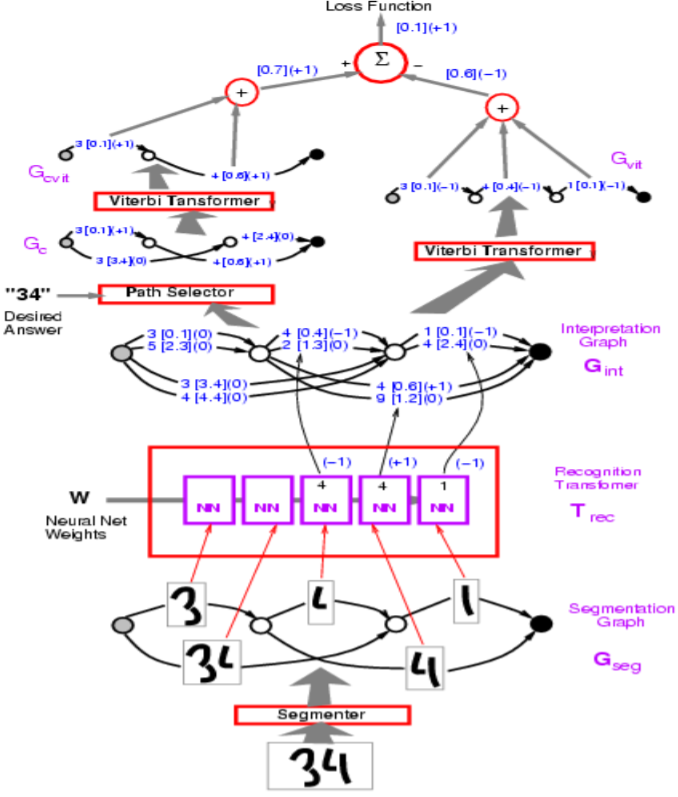
图 1: 网络结构
在上图中,错误的路径被标为 $-1$ 。
在上图中的例子中,Transformer图模型使用了Perceptron误差。我们的目标是使得错误答案的能量尽量大,正确答案的目标尽量小。
从算法实现的角度,你会用向量表示图示中的弧线。相比较于对每个类别使用不同的弧线,单个向量就同时包含了所有类别和每个类别的分数。
提问:上述模型中的分割模型是如何实现的?
回答:分割模型是人工启发式的。尽管有其他的方法可以实现端到端的训练,但该模型使用了一个人工的分割。这种人工方法在字母识别中被滑动窗口的方法所取代。
损失函数概述
| 损失函数 | 公式 | 边界 |
|---|---|---|
| Energy Loss | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)$ | None |
| Perceptron | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)-\min\limits_{\text{Y}\in\mathcal{Y}}\text{E}(\text{W}, \text{Y}, \text{X}^i)$ | 0 |
| Hinge | $\max\big(0, m + \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | $m$ |
| Log | $\log\bigg(1+\exp\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | >0 |
| LVQ2 | $\min\bigg(M, \max\big(0, \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | 0 |
| MCE | $\bigg(1+\exp\Big(-\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\Big)\bigg)^{-1}$ | >0 |
| Square-Square | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2-\bigg(\max\big(0, m - \text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)^2$ | $m$ |
| Square-Exp | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2 + \beta\exp\big(-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | >0 |
| NNL/MMI | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i) + \frac{1}{\beta}\log\int_{y\in\mathcal{Y}}\exp\big(-\beta\text{E}(\text{W}, y,\text{X}^i)\big)$ | >0 |
| MEE | $1-\frac{\exp\big(-\beta E(W,Y^i,X^i)\big)}{\int_{y\in\mathcal{Y}}\exp\big(-\beta E(W,y,X^i)\big)}$ | >0 |
Perceptron损失在上表中似乎没有边界,但也正因如此,这种损失存在数值爆炸的风险。
-
Hinge损失是偏差最大的答案和正确答案的能量差值。从直观上可以理解为,对于边界 $m$,当正确答案的能量至少低于偏差最大的答案的能量 $m$ 时,Hinge损失只会是0。
-
MCE损失被用于语音识别,看上去和Sigmoid相近。
-
NLL 损失的目标是使得正确答案的能量尽量小,并且使得公式中的对数部分尽量大。
提问:为什么Hinge损失比NLL损失更好?
回答:Hinge损失比NLL损失更好的原因为:NLL鼓励正确答案和其他答案的能量差值趋于无穷,而Hingle损失只鼓励差值大于固定数值(边界 $m$ )。
定义:
一个解码器以一串向量作为输入,这串向量表示分数或单独的声音/图像的能量,然后解码器选择其中最有可能的输出作为结果。
提问:什么问题可以使用解码器?
回答:语言模型,机器翻译或者序列标注。
Transformer图模型中的前向算法
图构成(Graph Composition)
我们可以通过图构成来结合两张图。在这个例子中,我们可以看到一个语言模型词典被表示为Trie图和一个用神经网络生成的识别图。
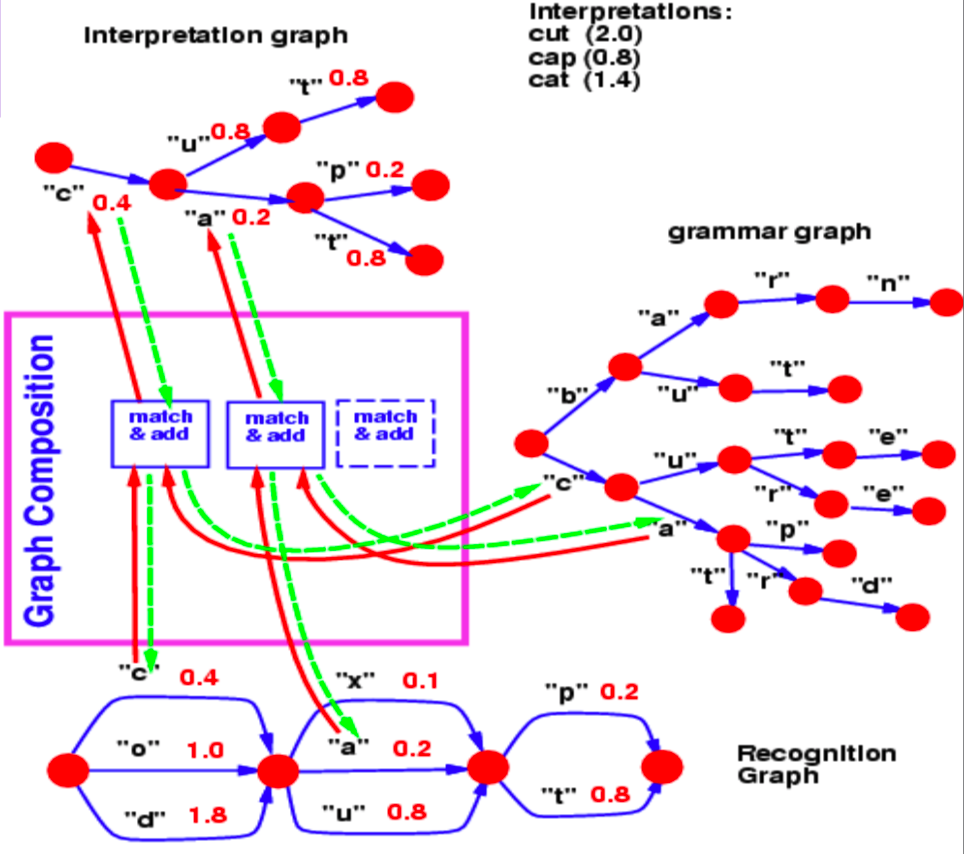
图 2: 图构成(Graph Composition)
识别图通过不同的能量数值(相对于每一条弧线)来标明一个字母在某个特别的步骤的可能性。
现在,我们想问一个关于图构成操作的问题作为例子:哪条在识别图中的路径是符合我们的词典的最佳路径?
识别图和语法图从第一步到第二步的共同的Hop是字母 $c$ ,相关联的能量是 $0.4$。因此,我们的解释图在第一步和第二步之间只包含了一条对应于 $c$ 的弧线。相似的,识别图中可能位于第二步和第三步间的字母为 $x$, $u$ 和 $a$。在语法图中位于 $c$ 之后的分支包含了 $u$ 和 $a$。所以,图构成操作选择了 $u$ 和 $a$ 作为解释图中的弧线。它也关联了从识别图中复制而来的弧线和对应的能量值。
如果语法图也包含了弧线上的能量值,图构成操作会添加这些能量值或把它们与其他的操作结合起来。
相似的,图构成也允许我们结合两个不同的用神经网络表达的知识。在上述示例中,一个预测下一字母的神经网络表达了语法。神经网络的Softmax输出向我们提供了从一个给定节点转移至下一节点的转移概率。
另外,如果例子中的语言模型是一个神经网络,我们可以在整个结构中进行反向传播。这就成为了一个包含了循环,条件判断,递归等操作的可以反向传播的可微分程序。
来自九十年代中期的支票读取器
来自九十年代中期的支票读取器的整体结构是比较复杂的,但我们主要感兴趣的部分从产生识别图的字母识别环节开始。
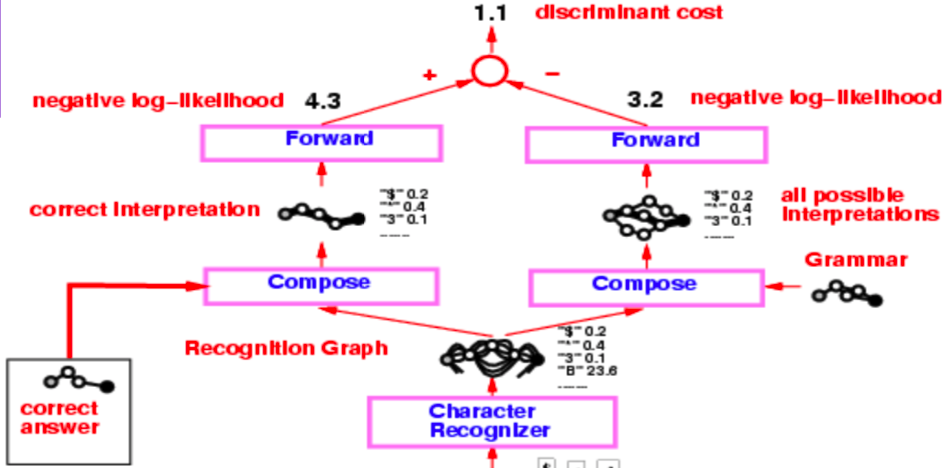
图 3: 支票读取器
识别图经过了两个独立的构成操作,第一个利用正确的解释(或者说真实值),第二个利用语法创建了包含所有可能解释的图。
整个系统通过Negative Log-Likelihood损失函数进行训练。Negative Log-likelihood表明解释图中的每条路径都是一种可能的解释,而这条路径上的能量和就是这个解释的能量。
现在,相比较于Viterbi算法,我们选择使用前向算法。在下一个小节我们将讨论这两种方法的区别。
Viterbi 算法
Viterbi算法是一种动态规划算法,它被用于找到指定图中最有可能的路径(拥有最小能量的路径)。它相对于隐变量 $z$ 优化能量使其最小,这里的 $z$ 代表图中的路径。
\[F (x, y) = \min_{z} \; E(x, y, z)\]前向算法
前向算法计算所有路径的负能量的指数之和的对数。这可以轻易地从以下的公式中看出:
\[F_{\beta} (x, y) = -\frac{1}{\beta} \; \log \; \sum_{z \, \in \, \text{paths}} \; \exp \, (- \beta \; E(x, y, z))\]这个操作在边缘化隐变量 $z$, 它定义了解释图中的路径。这种方法计算了抵达特定节点的所有可能路径的指数之和的对数。这就像在以一种软性最小化的方式结合所有可能路径的代价。
前向算法的实现十分节约资源并且不比Viterbi算法有更大的花费。而且,我们可以对图中所有前向算法节点进行反向传播。
前向传播的成功可以通过下面这个定义在解释图上的例子来证明。
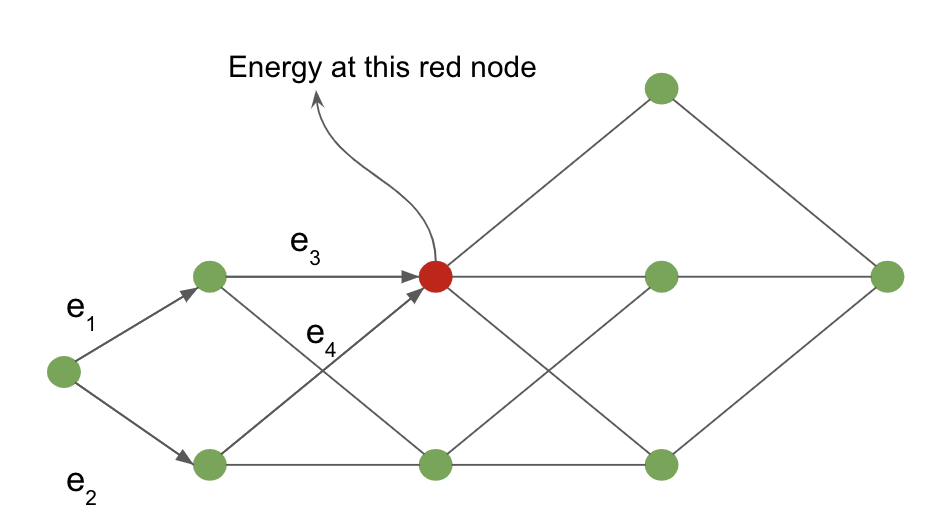
图 4: 解释图
从输入节点到红色阴影节点的代价是通过边缘化所有可能通向红色节点的路径。 在我们的例子中,指向红色的箭头定义了这些可能的路径。
对于红色节点,该节点的能量值为:
\[-\frac{1}{\beta} \; \log \; [ \, \exp \, (- \, \beta (e_1 \, + \, e_3)) \; + \; \exp \, (- \, \beta (e_2 \, + \, e_4)) \, ]\]前向传播算法的神经网络类比
前向算法是置信度传播算法在图蜕化为链图时特殊形式。整个算法可以被看做是一个前向传播的神经网络,每个节点函数为一个指数和的对数与一个额外项。
我们对于解释图中每一个节点都维护一个变量 $\alpha$。
\[\alpha_{i} = - \; \log \; \biggl[ \sum_{k \, \in \, \text{parent} \, (i)} \; \exp \, (- \, \beta \; (\alpha_k \, + \, e_{ki})) \biggl]\]其中的 $e_{ki}$ 是节点 $k$ 到节点 $i$ 的边的能量。
$\alpha_i$ 组成了神经网络中节点 $i$ 的激活值,而 $e_{ki}$ 是连接节点 $k$ 和 节点 $i$ 的边的权重。这样的模型在代数上等同于一个神经在对数域上的加权和操作。
我们可以对一个应用了前向算法的动态(对于不同的例子,图会改变)解释图进行反向传播。我们可以在图的末尾节点上对于定义在解释图的边上的边权重 $e_{ki}$ 计算梯度 $F(x, y)$。

图 5: 支票读取器
我们回到支票阅读器的例子,我们对两个图构成使用了前向算法并且通过使用指数和的对数的计算公式得到了末尾节点的能量值。这两个能量值的差值就是Negative log-likelihood 损失。
位于识别图和正确答案之间的在图构成上使用前向算法得到的的结果是正确答案的指数和的对数。相对的,位于识别图和语法图之间的图构成上最后一个节点的指数和的对数,是所有可能可行解释的边缘值。
反向传播的拉格朗日形式
对于输入 $x$ 和 目标输出 $y$, 我们可以用一系列函数建模一个网络。$f_k$ 作为权重,$w_k$ 用于网络输出 $z_k$ 之后的步骤 $z_{k+1} = f_k(z_k, w_k)$。在监督学习的设定中,网络的优化目标是最小化网络的第 $n$ 个结果相对于真值的代价:$C(z_n, y)$,这等价于相对于限制条件 $z_{k+1} = f_k(z_k, w_k)$ 和 $z_0 = x$,最小化 $C(z_n, y)$。
拉格朗日项可以被写作:
\(\mathcal{L}(x, y, \lambda_i, z_i, w_i) = C(z_n, y) + \sum\limits_{k=0}^{n-1} \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k))\)
其中 $\lambda$ 项表示拉格朗日乘子 (详见 Paul’s online notes 作为复习材料)。
为了最小化 $\mathcal{L}$, 我们需要将$\mathcal{L}$ 相对于每个输入的偏导数设为 $0$ 并求解。
-
对于 $\lambda$, 我们简单地将该限制条件还原:$\frac{\partial{\mathcal{L}}}{\partial \lambda_{k+1}} = 0 \rightarrow z_{k+1} = f_k(z_k, w_k)$。
-
对于 $z_k$, $\frac{\partial \mathcal{L}}{\partial z_k} = 0 \rightarrow \lambda^T_k - \lambda^T_{k+1} \frac{\partial f_k(z_k, w)}{\partial z_k} \rightarrow \lambda_k = \frac{\partial f_k(z_k, w_k)^T}{\partial z_k}\lambda_{k+1}$, 这一步只是标准的反向传播公式。
这个方法由拉格朗日和汉密尔顿在经典力学的背景下提出,其中最小化的目标是整个系统的能量,而 $\lambda$ 项表示了系统的物理限制,例如:两个球被一个铁杆限制在固定距离内。
在我们需要每步优化代价 $C$ 的情况下,拉格朗日项变为 \(\mathcal{L} = \sum_k \left(C_k(z_k, y_k) + \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k)) \right)\).
神经偏微分方程
通过采用这种形式的反向传播,我们可以讨论一种新模型:神经偏微分方程(Neural ODEs)。这些网络大体上是一种循环神经网络,其中,$t$ 时刻的状态 $z$ 被定义为 $ z_{t+\text{d}t} = z_t + f(z_t, W) dt $。$W$ 代表一些固定的参数。这也可以用普通的微分方程(非偏微分方程)来表达:$\frac{\text{d}z}{\text{d}t} = f(z_t, W)$。
通过采用朗格朗日公式来训练这样的网络是十分直接的。如果我们拥有目标 $y$ ,并且我们希望系统状态在时刻 $T$ 到达 $y$,我们可以简单将代价函数设为 $z_T$ 和 $y$ 的距离。网络的另一个目标可以是找到系统的稳定状态,比如,在某时刻后,系统不再改变。从数学上说,这等同于 $\frac{\text{d}z}{\text{d}t} = f(y, W) = 0$ 的设定。总体来说,使用这种方法找到一个方程的解 $y$ 比反向传播更容易,因为网络不需要记住相对于整个序列的梯度,并只需要优化 $f$ 或 $\lvert f \rvert^2$。对于更多训练神经偏微分方程来达到不动点的信息,可以参考 (Lecun88)。
能量角度的变分推断
对于一个基本的能量函数 $E(x,y,z)$, 如果我们想要针对一个变量 $z$ 边缘化以获得一个只包含 $x$ 和 $y$ 的损失 $L(x,y)$, 我们必须计算
\[L(x,y) = -\frac{1}{\beta}\int_z \exp(-\beta E(x,y,z))\]如果我们乘上 $\frac{q(z)}{q(z)}$, 我们会获得
\[L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\]如果我们假设 $q(z)$ 是 $z$ 的概率分布,我们可以把我们重写后的损失函数中的积分结果解释为一个相对于 $\frac{\exp({-\beta E(x,y,z)})}{q(z)}$ 的分布的期待值。
我们使用这种解释,琴生不等式和基于采样的估计,来间接地优化我们的损失函数。
琴生不等式
琴生不等式是以下情况的一种几何观察:如果我们有一个凸函数,那么处于一定范围的函数的期待值是这个函数在范围两端的结果的平均值。从几何上展示这一点是十分直观的:
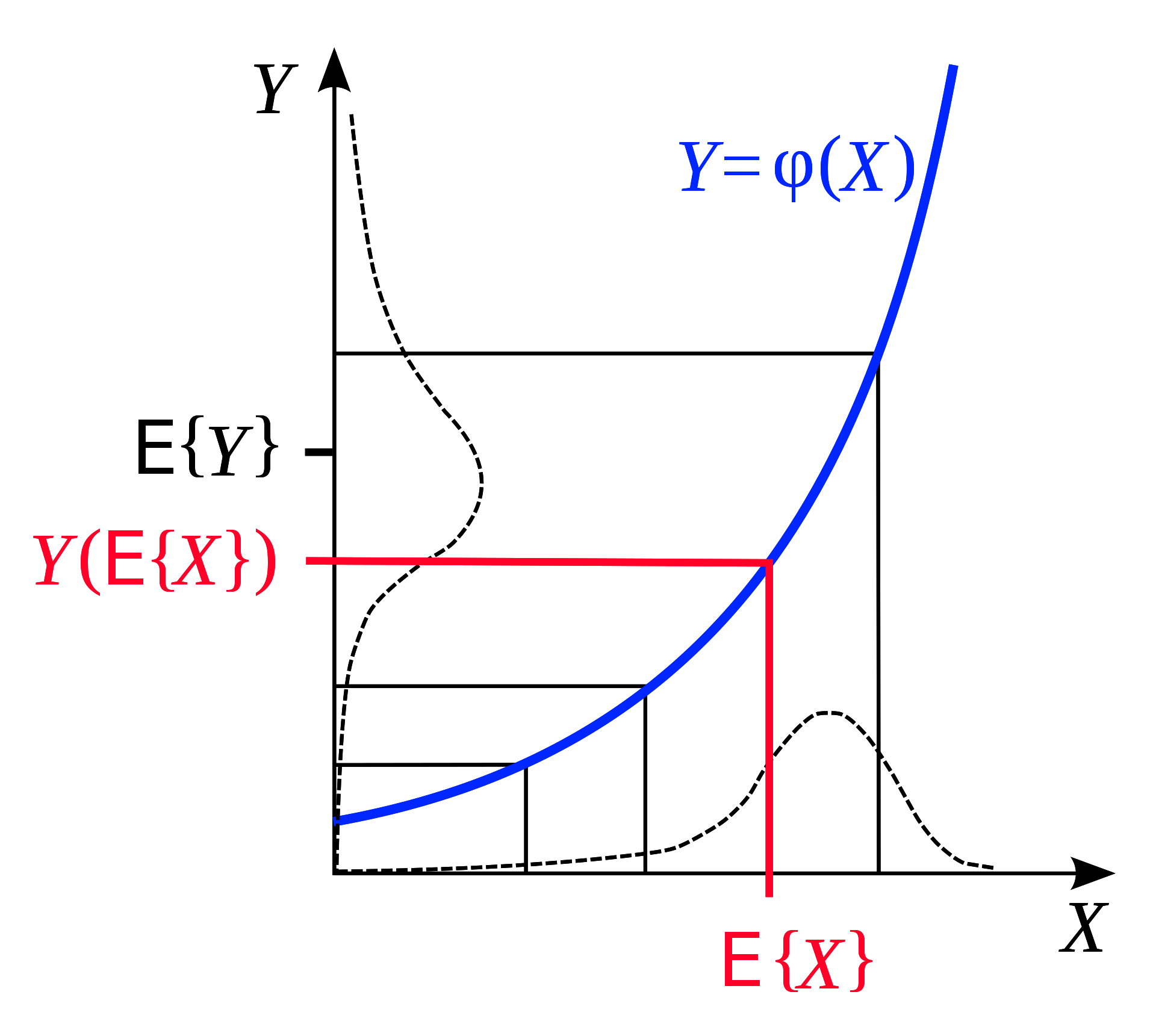
图 6: 琴生不等式 (来源 [Wikipedia](https://en.wikipedia.org/wiki/Jensen%27s_inequality))
类似的,如果 $F$ 是凸的,那么对于一个固定的概率分布 $q$, 我们可以通过琴生不等式推得,在一定范围 $z$ 上,
\[F\Bigg(\int_z q(z)h(z)\Bigg) \leq \int_z q(z)F(h(z)) \tag{1}\]现在,回想起我们的边缘化后的乘上了 $\frac{q(z)}{q(z)}$ 的 $L(x,y)$
\[L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\]如果我们令 $h(z) = -\frac{1}{\beta} \frac{\exp({-\beta E(x,y,z)})}{q(z)}$,我们可以从琴生不等式 $(1)$ 得到
\[F\Bigg(\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z)F\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\]我们再用一个具体的凸损失函数,$F(x) = -\log(x)$
\[-\log\Bigg(-\frac{1}{\beta}\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z) * \frac{-1}{\beta}\log\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\] \[\leq \int_z q(z)[E(x,y,z) + \frac{1}{\beta}\log(q(z))]\] \[\leq \int_z q(z)E(x,y,z) + \frac{1}{\beta}\int_z q(z)\log(q(z))\]很好!现在我们通过两个我们能够理解的项得到了我们的损失函数 $L(x,y)$ 的上界,第一项 $\int_z q(z)E(x,y,z)$ 是平均 能量,第二项 $\frac{1}{\beta}\int_z\log(q(z))$ 是分布 $q$ 的熵 乘上了一个标量($-\frac{1}{\beta}$)。
要点
我们现在通过一种方法表达了上界,这种方法避免了复杂的积分,而采用在一个我们选择的替代分布( $q(z)$ )上采样来简单估计这些值。
为了得到我们的上界公式的第一项,我们只需要在这个分布中采样,并计算采用了我们采样的 $z$ 的 $L$ 的平均值。
第二项(熵的倍数)只是这种分布的一个特点,可以被相似地使用随机采样 $q$ 来估计。
最后,我们通过最小化 $L$ 的上界来相对于$L$ 的参数 (网络权重 $W$)最小化 $L$。我们通过更新两个变量来优化:(1)$q$ 的熵 (2)模型参数 $W$。
总结
本章节从能量角度看待变分推断(variantonal inference)。如果你需要计算指数之和的对数,你可以用你的损失函数的平均值加上一个熵项来替换。这样的替换提供了一个上界。接着我们最小化这个上界,从而最小化我们的损失函数。
📝 Yada Pruksachatkun, Ananya Harsh Jha, Joseph Morag, Dan Jefferys-White, and Brian Kelly
Yang Zhou
4 May 2020