用于结构化预测的深度学习

结构化预测

结构化预测这种问题是对给定的输入 x 预测变数 y，其中输出值彼此相关且带有限制，而是离散或实数的标量。并且输出的变数并非属于特定的类别，而是具有指数多个或者无穷多的可能值。 例如：在语音识别、手写识别，或是自然语言翻译，输出必须符合语法，而且不能限制可能的输出的数量。模型的工作为捕捉在问题领域的循序、空间、或组合的结构。

结构化预测的早期工作

这个向量被喂给一个 TDNN（时延神经网络），它给出一个特征向量（等同代表类别的 softmax）。其中一个语音识别遇到的状况是，同一个词可能不同的人发音速度或方法不同。我们使用动态时间规整来解决这个问题。

想法是为系统提供一组预先录制，对应到录下的某人的序列或者特征向量的模板。神经网络训练时同时使用这些模板，使得系统学会识别不同发音下的词汇。潜变量使我们得以将特征向量延时以配合模板的长度。

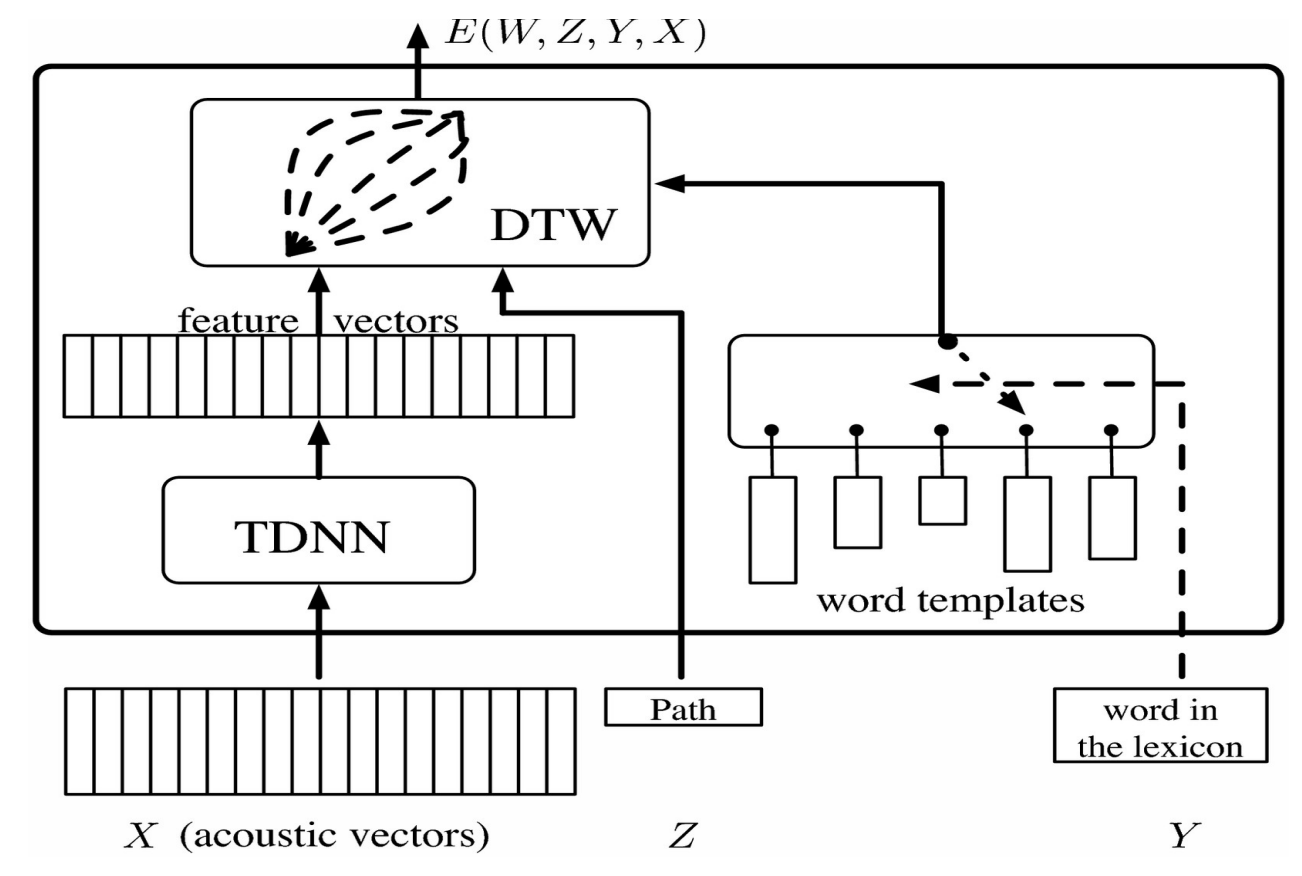
Figure 1.

这可以视觉化为矩阵，藉由将来自 TDNN 的特征向量水平排列，词汇模板垂直排列。矩阵中的每个元素对应到特征向量间的距离。这可以视觉化为一个图的问题：目标是从左下角以最短路径抵达右上角。

为训练这个潜变数模型，我们得使正确答案的能量尽量小，错误答案的能量尽可能大。为此我们使用一个目标函数，它会接收错误词汇的模板并且将它们推离目前的特征序列，并且将梯度反向传播。

基于能量的因子图

基于能量的因子图的想法是要建立一个能量基础模型，其中的能量是各项部份的能量的和或者当几率是因子的积。这些模型的优点是可以利用高效的推断算法。

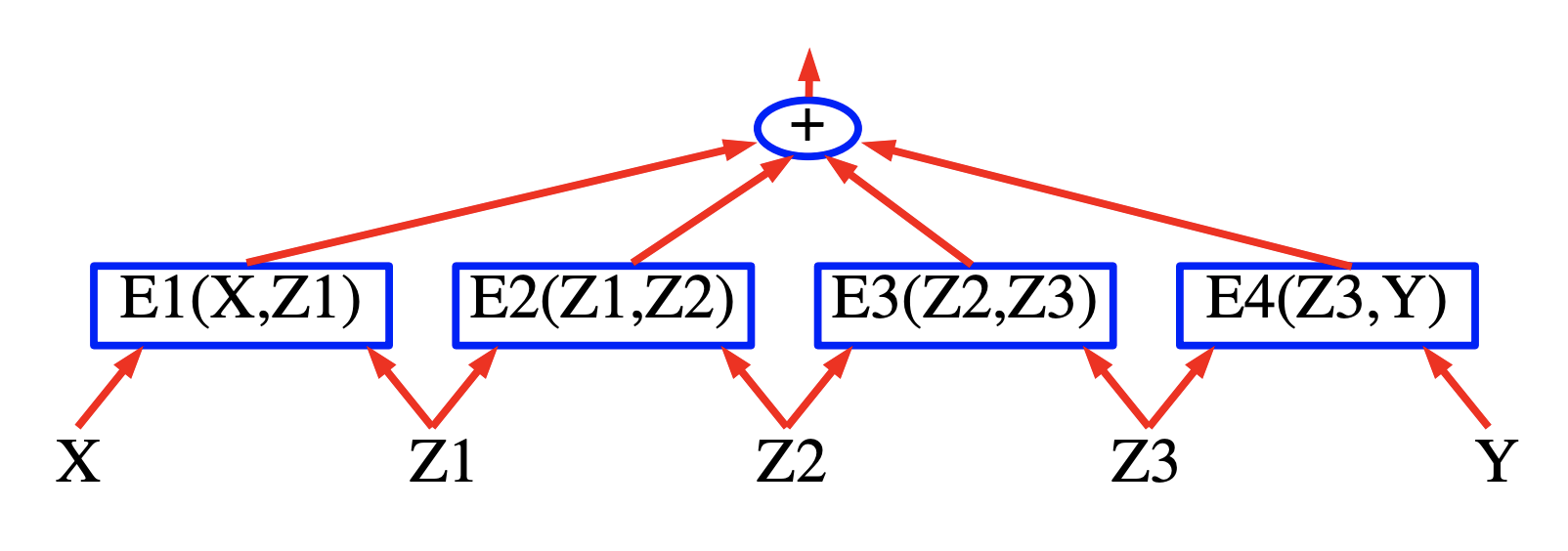
Figure 2.

序列标记

模型接受一个说话的声音讯号 X 并输出使得总能量最小化的标记 Y。

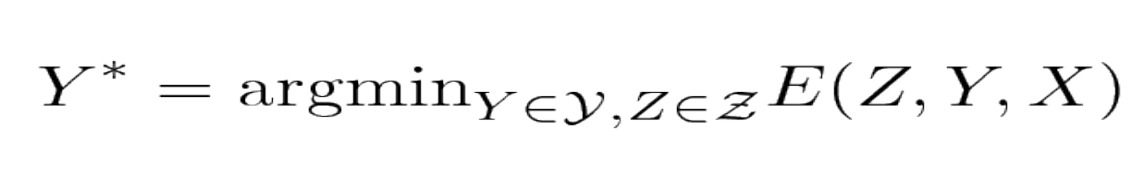
Figure 3.

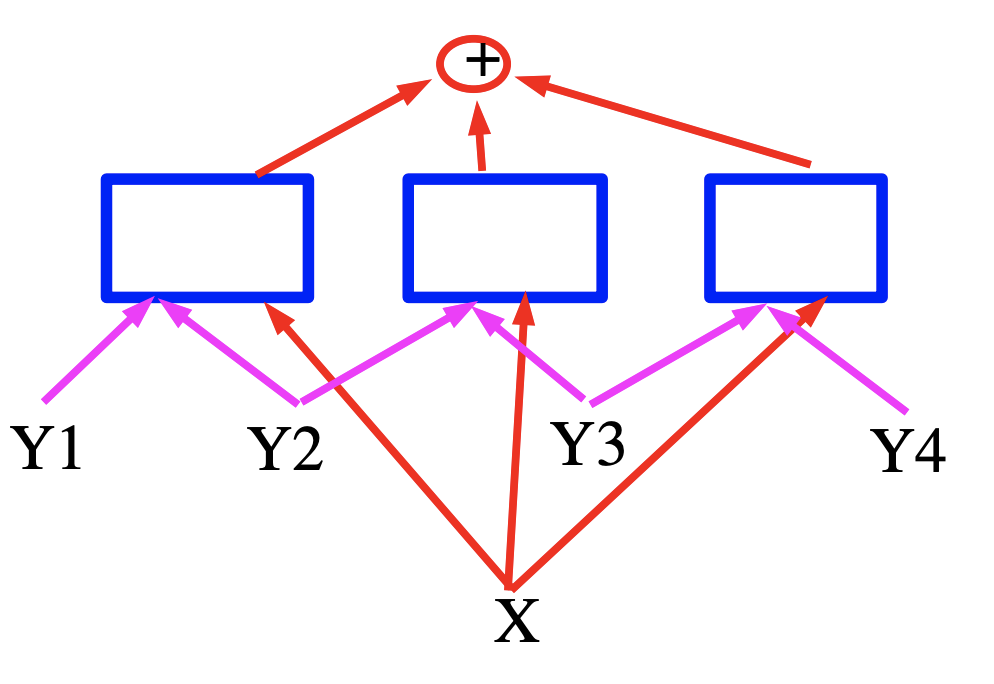
Figure 4.

此处，能量是蓝色方块代表的三个项，也就是为输入变数产生特征向量的神经网络。就语音识别而言，X 可以想作声音讯号，方块实作文法限制，而 Y 代表生成的输出标记。

基于能量的因子图的高效推断

能量基础学习教程 (Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, and Fu Jie Huang 2006)：

用能量基础模型进行学习与预测牵涉到最小化答案 $\mathcal{Y}$ 和潜变数 $\mathcal{Z}$ 的能量。当 $\mathcal{Y} \times \mathcal{Z}$ 的基数很大时，最小化的过程可能变得难以追踪。其中一种解法是善用能量函数的结构以有效最小化。一种能善用结构的例子是当能量能被表达为一些函数（称作因子）的和，而这些函数各自依赖于 Y 和 Z 中不同组变数的子集。这些依赖适合用因子图的方式来表示。因子图是一种概率图模型或信念网络的一般型。

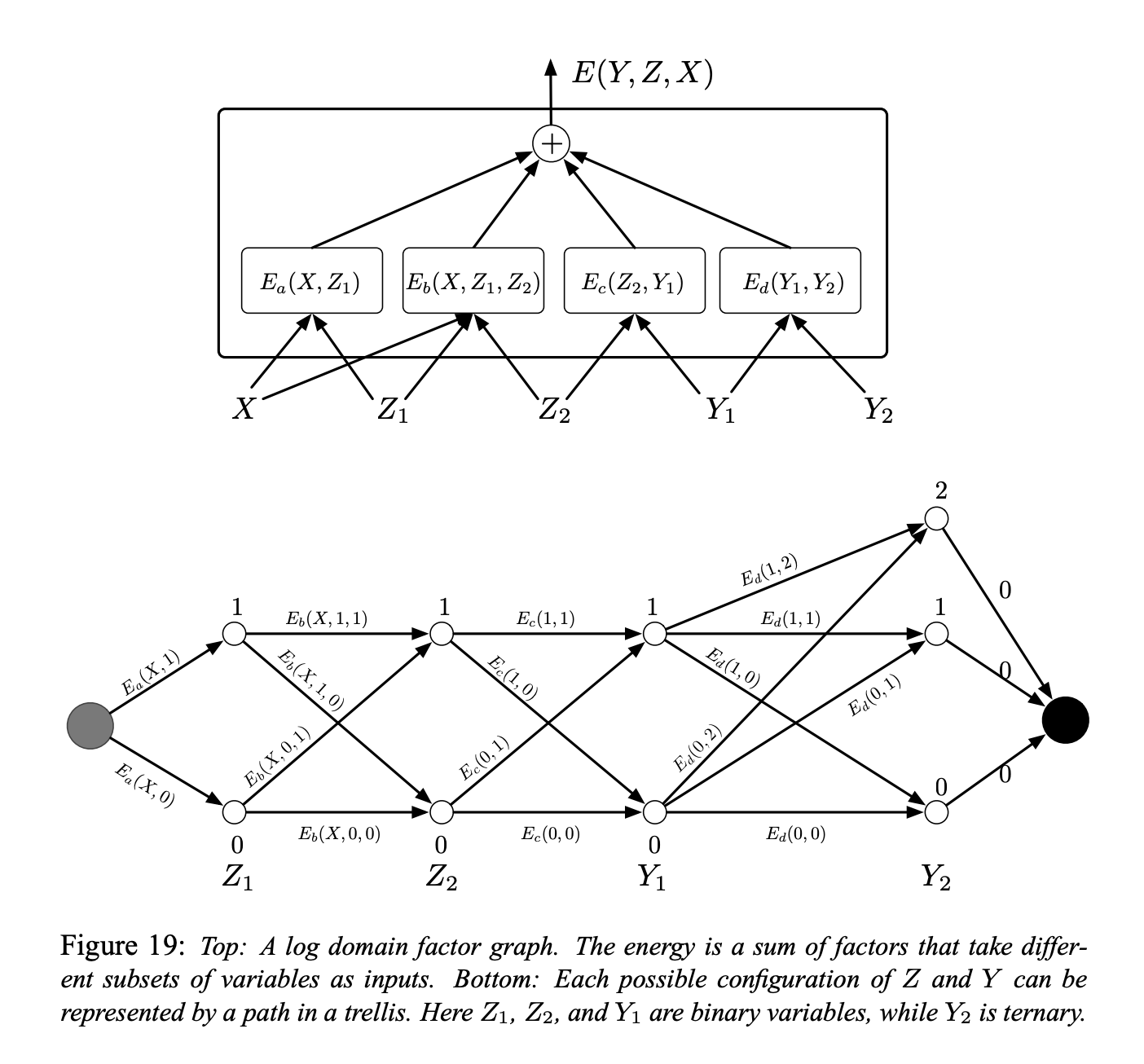
Figure 5.

Figure 19 展示了一个单纯的因子图。能量函数是四个因子的和：

其中 $Y = [Y_1, Y_2]$ 是输出变数，$Z = [Z_1, Z_2]$ 是潜变数。每个因子可视为代表对输入变数的软性限制。推断的问题是要找：

先假定 $Z_1$, $Z_2$, 和 $Y_1$ 是离散的二元变数，$Y_2$ 是三元变数。$X$ 的定义域的基数并不重要，因为 X 总是会被观测。给定 X 之下 $Z$ 和 $Y$ 可能的组合的数量有 $2 \times 2 \times 2 \times 3 = 24$。一个朴素的，经由穷举的最小化算法会计算能量函数 24 次（96 次的因子计算）。

然而，我们注意到对给定的 $X$，$E_a$ 只有两种可能的输入组合：$Z_1 = 0$ 和 $Z_1 = 1$。相似地，$E_b$ 和 $E_c$ 只有 4 种可能的输入组合，而 $E_d$ 有 6 种。总共只需要 $2 + 4 + 4 + 6 = 16$ 单一的因子计算。

因此，我们可以预先计算 16 个因子的数值，如 Figure 19（下方）将它们放在格子中的弧上。

每一列的节点代表一个变数的可能值。每个边的权重是因子根据对应输入变数输出的能量。在这种表示之下，一个从开始节点到最终节点的路径代表一种可能的变数组合。路径权重的和代表该组合的能量。故推断的问题可以归约为寻找图中的最短路径，能够运用动态规划的方法例如 Viterbi 算法或者 A* 算法来解决。损失会与边的数量成比例（16），也就是指数小于总共的路径数量。

要计算 $E(Y, X) = \min_{z\in Z} E(Y, z, X)$ 时，使用同样的程序，只是我们会将图限制到那些跟定下的 $Y$ 相容的弧的子集。

以上的程序有时被称作 min-sum 算法，它是传统的图的 max-product 算法的对数域版本。这个过程很容易能推广到接受多于两个变数输入的因子图，和树状结构而非链状结构的因子图。

然而，它仅适用于二分树（无环）的因子图。当图里有环，min-sum 算法可能给出近似解，也可能完全不收敛。此时可以使用如模拟退火这种下降算法。

单纯的，具有浅的因子的基于能量的因子图

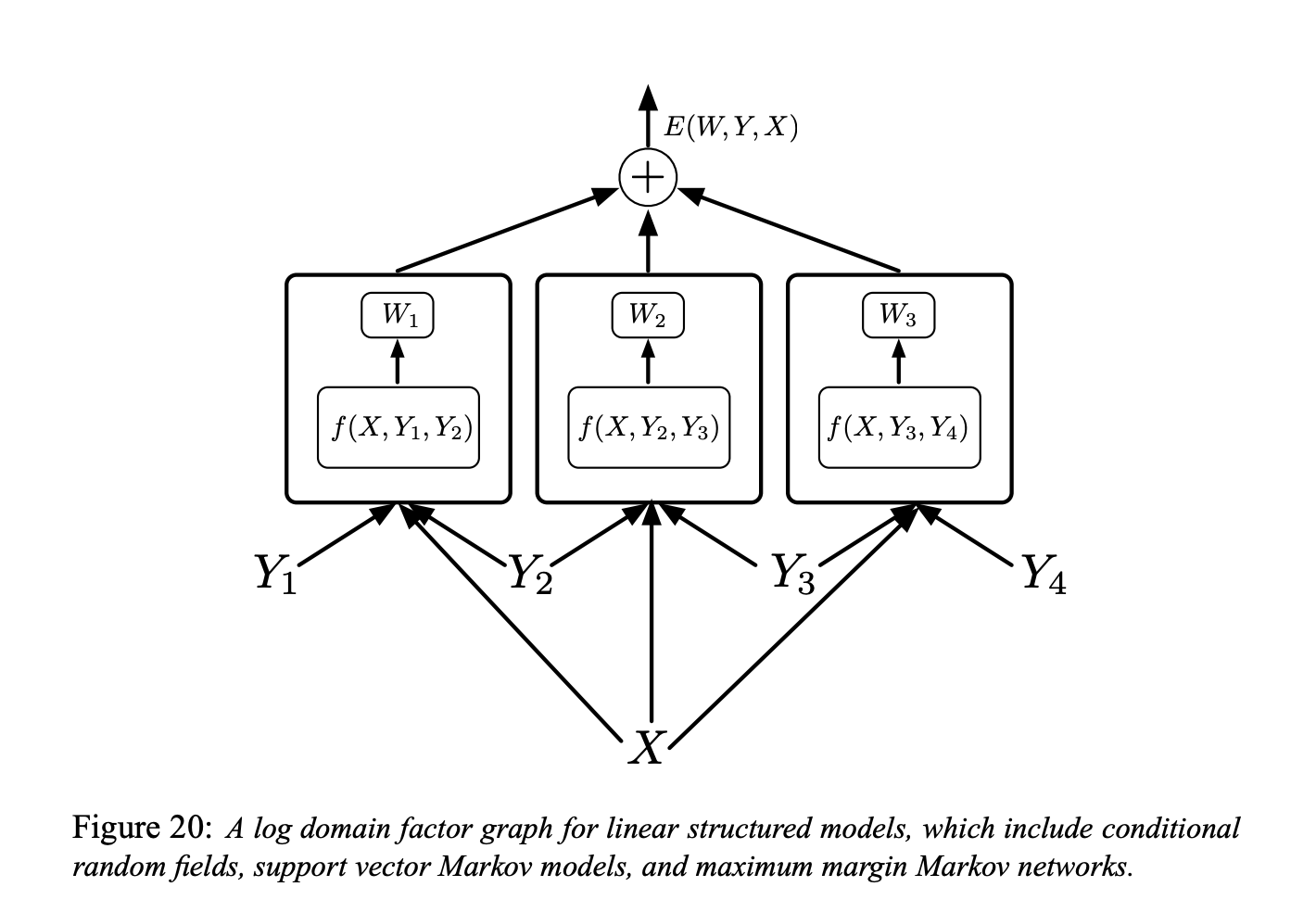
Figure 6.

Figure 20 中是在对数域中线性结构模型的因子图（也就是我们所说单纯的，具有浅的因子的基于能量的因子图）。

每个因子都是具有可训练参数的线性模型。它依赖于输入与一对的标记 $(Y_m, Y_n)$。总的来说，每个因子都可以依赖于超过两个标记，但我们会只讨论成对的因子来简化符号：

这里 $\mathcal{F}$ 代表因子的集合（一对对有着直接互相依赖的关系的标记的集合），$W_{m n}$ 是因子 $(m, n)$ 的参数，而 $f_{m n}\left(X, Y_{m}, Y_{n}\right)$ 是个（固定的）特征向量。全域的参数向量 $W$ 是串接所有 $W_{m n}$。

接着我们可以想想要用何种损失函数，这里有几种模型。

条件随机场

我们可以用负对数似然损失函数来训练一个线性结构模型。

这是条件随机场。

直觉上来说，我们希望正确答案的能量要小，而所有答案（包含那些较好的）的指数取对数之后要大。

底下是负对数似然损失的正式定义：

最大边界马可夫网络与潜支持向量机

我们也可以用合页损失做优化。

想法是我们希望正确答案的能量可以很小，而在所有可能的错误答案中，找到有着最低能量的。接着我们要增加它的能量。其它答案就不用，因为它们已经有较高的能量。

这就是最大边界马可夫网络和潜支持向量机的概念。

结构化感知器模型

我们可以用感知器损失训练线性结构化模型。

Collins [Collins, 2000, Collins, 2002] 提倡在 NLP 使用感知器损失：

其中 $Y^{* i}=\operatorname{argmin}_{y \in \mathcal{Y}} E\left(W, y, X^{i}\right)$ 是系统找到的答案。

早期用于语音、手写识别的判别训练

最小经验误差损失 (Ljolje, and Rabiner 1990)：

在序列的层次进行训练，他们不告诉系统对应的声音或位置，而是给系统输入的语句和逐字稿，并且要系统藉延时自己找出来。他们并没有使用神经网络，而是使用其它方法把语音信号转为声音类别。

图变换网路

这里的问题是我们有一个数字的序列作为输入但不知如何分段。我们可以建立一个图其中每个路径都是一种分段方法，接着找出最小能量的路径，基本上就是找最短路径。这里是一个具体的示例。

我们有输入图像 34。将其输入分段器，得到多种分割方法。这些分段都是可以组合小区段的方式。每一道路径都对应到一种组合这些笔迹的方式。

Figure 7.

我们将每一种都输入相同的字元识别卷积网络，得到 10 个分数（这里写了 2 个但是应该有 10 个，对应 10 个分类）。举例来说，1 [0.1] 代表类别 1 的能量是 0.1。所以这里有一个图，或者想像成一个奇怪的张量。它其实是一个稀疏的张量。这张量标明每一种变数的组合的损失。其实它更像是张量的一个分部，或者是对数分布因为我们讨论的是能量。

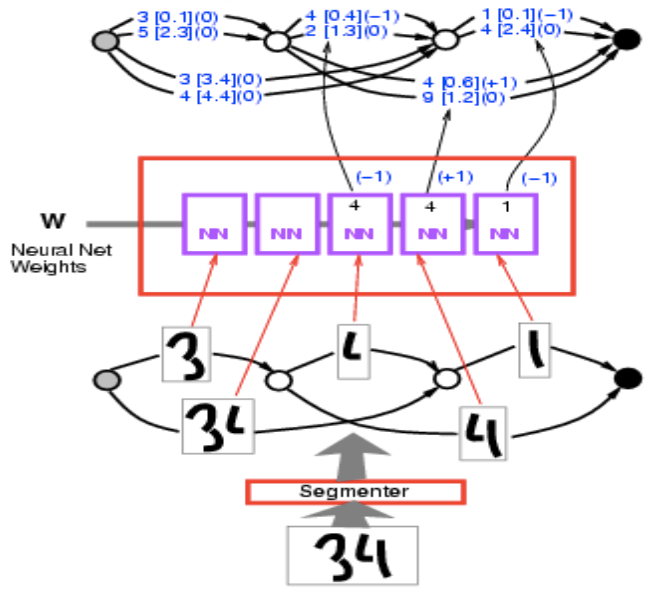
Figure 8.

拿到这个图之后我们要来计算正确答案的能量。我先说正确解答是 34。找到抵达 34 的路径，有两个，能量各自为 3.4 + 2.4 = 5.8 和 0.1 + 0.6 = 0.7。选择有最低能量的路径，这里就是 0.7。

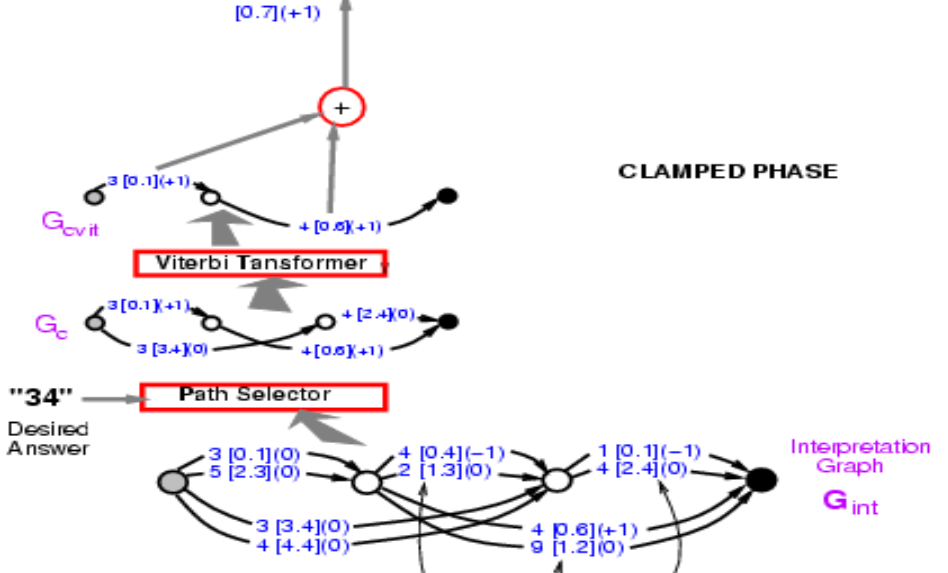
Figure 9.

所以寻找路径就像最小化潜变数，其中潜变数是我们选择的路径。概念上而言，它是一个以潜变数为路径的能量模型。

我们已经算出正确路径的能量：0.7。我们现在所需要做的就是将梯度反向传播，以改变卷积网络中的权重，使总能量下降。虽然看起来很困难，但完全是办的到的。因为整个系统都是由我们已知的元素组成，神经网络是普通的，路径选择器和 Viterbi 转换器只是表达是否选择某个边的开关。

那要如何反向传播呢？首先点 0.7 是 0.1 + 0.6。所以点 0.1 和 0.6 的梯度是 +1，如括弧内所写。接下来，Viterbi 转换器只是在两条路径中择一，所以只要把梯度复制到对应的边并将其他边设为 0，正如使用最大值池化或平均值池化时一样。路径选择器的情况也是一样，只是选择正确答案的系统。注意图中的 3 [0.1] (0) 在此刻应该是 3 [0.1] (1)，我们稍后会回到这里。接着你可以在网络中反向传播梯度，以减低正确答案的能量。

重要的是，这个结构是动态的，因为当我们收到一个新的输入，神经网络的数量会随着分段的数量而改变，导出的图也会不同。我们必须反向传播过这个动态结构。这就是 PyTorch 能派上用场的地方了。

这一阶段的反向传播使正确答案的能量变小。而在第二阶段我们要使错误答案的能量上升。此时，我们让系统任意选择它要的答案，进行一种简化的判别训练做结构化预测，并使用感知器损失。

第二阶段的第一步和第一阶段完全相同。Viterbi 转换器选择有着最低能量的路径，我们不在乎到底是正确与否。此处得到的能量会小于等于第一阶段得到的，因为我们按照最小能量选择路径。

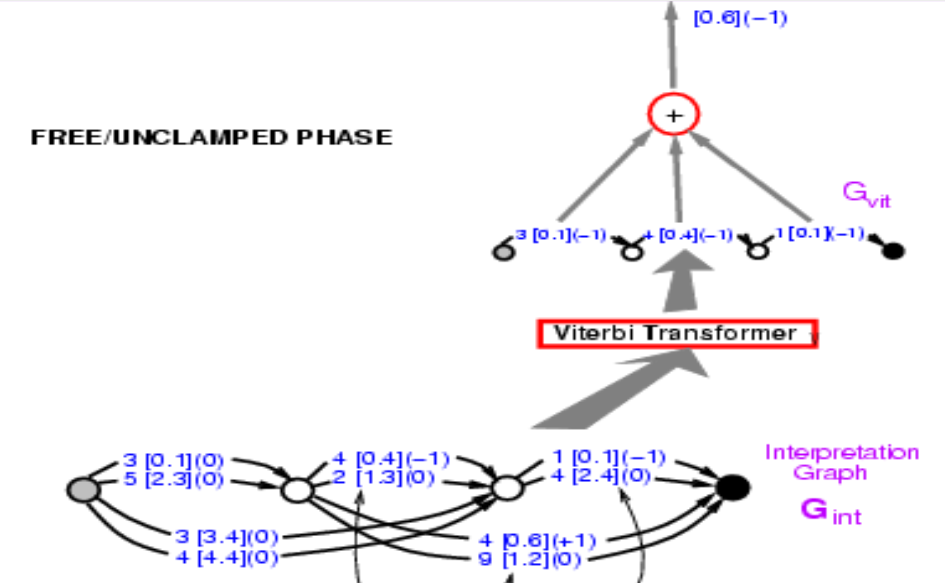
Figure 10.

将两阶段放在一起，损失函数应该要是第一阶段能量减去第二阶段的能量。之前我们介绍了如何在左半边反向传播，我们现在要在整个结构中反向传播。在左边的路经会得到 +1，而右侧的路径会是 -1，所以 3 [0.1] 出现在两边，应该得到梯度 0。这样做最终系统会最小化正确答案和最佳答案之间的能量插。这里的损失函数是感知机损失。

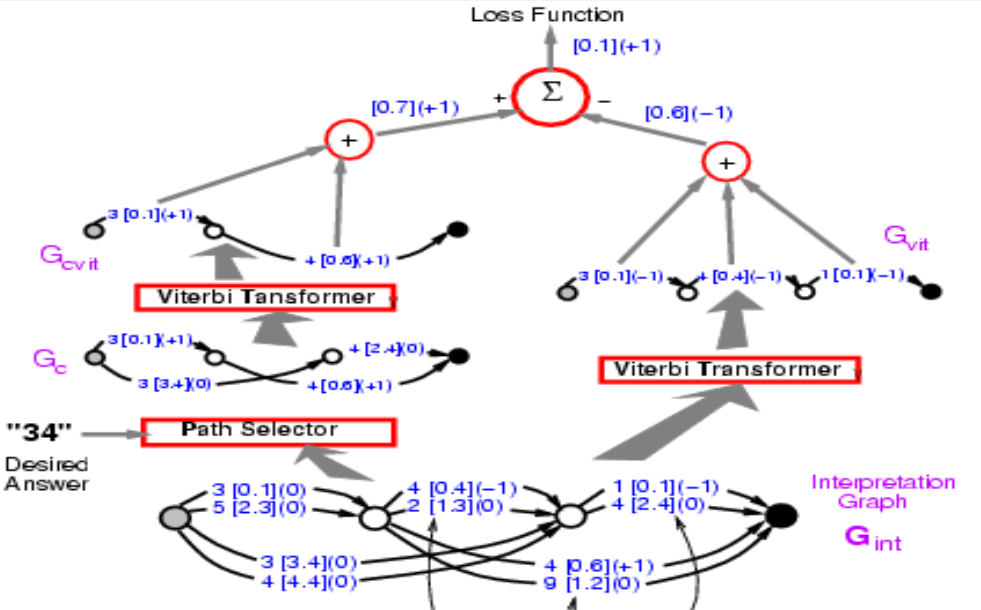
Figure 11.

理解问答

问题 1：为何基于能量的因子图的推断很容易？

在具有潜变数的能量基础模型中，推断需要使用穷举的方法例如梯度下降来最小化能量，然而在此的能量可以由各因子累加，能够用动态规划的技巧处理。

问题 2：如果因子图中的潜变数是连续变数呢？我们还是能使用 min-sum 算法吗？

不能，因为这样无法寻找所有可能组合。然而，此时能量也给我们一个好处，因为我们可以做独立优化。像在 Figure 19 中 $Z_1$ 和 $Z_2$ 只影响 $E_b$。我们可以做独立的优化和动态规划来进行推断。

问题 3：NN 的箱子是指不同的卷积网络吗？

他们是共用的。只是同一个字元识别网络的多个复制。