图形卷积网络 II

光谱图形卷积网络(Spectral Graph ConvNets , 英文简称GCNs)

在之前的部份，我們討論了圖形卷積網絡的理論，用兩個方法之一來決定用在圖形上的捲積，也我們現在能夠用來決定我們的光譜圖形卷積網絡。

基本型的光譜圖形卷積網絡(Vanilla Spectral GCN)

我們定義了一個圖形光譜層，比如我們叫它為$h^l$，這個下一層的激活值是這樣:

這裡的$\eta$代表一個非線性激活和$w^l$代表一個空間性的過濾器。這個方程的 右側是等於$\eta(\hat{w}^l(\Delta)h^l)$，這裡的$\hat{w}^l$代表一個光譜過濾器，而$\Delta$是拉普拉斯(Laplacian)。我們可以更進一步分解程式的右側為$\eta(\boldsymbol{\phi} \hat{w}^l(\Lambda)\boldsymbol{\phi^\top} h^l)$，而$\boldsymbol{\phi}$是就是傅立葉矩陣(Fourier matrix)和$\Lambda$是特徵值。這就生成下方最後的程式。

目標是為了用反向傳播，而不是人手外加的，去學到一個光譜過濾器 $\hat{w}^l(\lambda)$。

這個方法過去時第一個用在卷積網路上的光譜性技巧，但它有多個局限性:

• 無法保證有空間區域性的過濾器
• 要去學由($\hat{w}(\lambda_1)$ 到 $\hat{w}(\lambda_n)$)每一層的O(n)那麼多的參數
• 學習率是$O(n^2$)因為$\boldsymbol{\phi}$是緊密矩陣(dense matrix)

樣條式圖形卷積網絡(SplineGCNs)

樣條式圖形卷積網絡涉及計算平穩的空間性過濾器來取得一些空間區域性的過濾器。這個在頻域和在空間區域性的關係是由帕塞瓦爾恆等式(Parseval’s identity)和也包括海森堡不確定性原理(Heisenberg uncertainty principle)一起建立出來的，方式是這樣:光譜過濾器的導數中較細的數值(較平穩的函數)$\Leftrightarrow$空間性(區域)過濾器中較細的方差。

我們如何去取得一個平穩的光譜過濾器?我們分解光譜過濾器我們如何去取得一個平穩的光譜過濾器?我們把光譜過濾器分解為$K$平穩內核$\boldsymbol{B}$(樣條，英文:splines)的線性組合，所以$\hat{w}^l(\Lambda)=diag(\boldsymbol{B}w^l)$，(diag: 對角矩陣)。這個激活方程式是如下方這樣。

\(h^{l+1}=\eta\bigg(\boldsymbol{\phi} \Big(\text{diag}(\boldsymbol{B}w^l)\Big)\boldsymbol{\phi^\top} h^l\bigg)\) (diag: 對角矩陣)

現在，我們只有$O(1)$個參數，參數為常數$K$，每層的參數是可以由反向傳播進行學習。相反，學習的複雜度還是$O(n^2)$。

重疊式圖形卷積網絡(LapGCNs)

我们如何在图形大小为$n$的，而只用一个线性的$O(n)$时间如何去学习?那使用拉普拉斯特征向量的直接带来的效果为$O(n^2)$复杂度。我们要避免「特征分解」，这一点可以由一个直接地学习一点个函数做到。这个光谱函数会是单项式的拉普拉斯，下方所示。

一个很好的功能就是过滤器是完全地被所有k-hop连接起来，看起来就如被k-hop支撑起来一样(这称为k-hop supports.)。

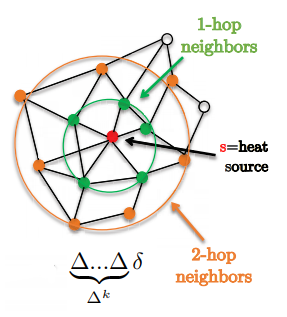
图1: 展示1-hop和2-hop邻域

我们替换表达式「$\Delta^k 」为「$X_k$」，一个递归方程式就如这样定义

那现在，稀疏（现实中）图形的复杂度现在为$O(E.K)=O(n)$。我们可以把$X_k$的大小转为$\bar{X}$来构成一个线性运算。我们现在就有下方这个激活方程。

注意: 因为没有用上拉普拉斯特征分解，所有运算都是在空间的域，而不是光谱性的域，所以叫它们为光谱式图形卷积网络是有点误导性的。更进一步的，重叠式图形卷积网络另一个缺陷就是卷积层是包含稀疏线性运算，也就是现在的GPU们不是在这方面有被完全优化过。

我们现在用这三个做法解决了三个基本版图形卷积网络的限制，第一是用位置性过滤器($K$-hop support)，第二是用每层为$O(1)$参数，第二是用$O(n)$学习复杂度。不过，重叠式图形卷积网络的限制是因为用了单项式基底($\Delta^0,\Delta^1,\ldots$)，这些基底是在优化中不稳定的，因为它不是正交的，也就是改变一个系数就改变函数的近似值。

切布网路(ChebNets)

为了去解决这个不稳定基底问题，我们可以用任何正交基底，但它必须要有一个递归方程式来确保有一个线性复杂度。对于切布网路，我们用切比雪夫多项式，而在重疊式圖形卷積網絡中，我們用$X_k$,來代表這個表達式$T_k(\Delta)h$，也就是在$h$上用上了切比雪夫函數的表達式，這樣一個遞歸方程就如下方定義，

現在我們就在系数扰动(coefficient perturbation)下有穩定性。

切布网路們都是圖形卷積網絡，它能夠用在任何任意的圖形領域上，但限制是它們都是各向同性的。標準的卷積网生成各向異性的過濾器，那是因為歐幾里得格子(Euclidean grids)是有方向的，同時光譜圖形卷積網絡計算各向同性過濾器，這是因為國形沒有方向這個概念，比如上下左右。我們可以延伸切佈網路到多重使用一個2d光譜過濾器的圖形。這或許是有用的，比如，在推薦系統中，我們有影片圖形和用戶圖形。多重圖形切佈網路有激活方程，下方所示。

凱利網路(CayleyNets)

凱利網路在其對應的頻段中生成局部性過濾器時，就生成得不穩定，而這是在眾多圖形中看得出來的。在凱利網路中，我們改為使用正交基底凱利有理化數(orthonormal basis Cayley rationals.)。

凱利網路有與切佈網路那樣有同樣的屬性，它們都是各向同性，但它們以帶光譜放大來以頻率來分佈，而且在同樣的$K$順序下，它也提供一個能分更多類的過濾器。

光谱图形卷积网络

模板匹配

为了明白光谱图形卷积网络，我们回到卷积网的模组匹配(template matching)的定义。

当给图形进行模组匹配的主要问题是模组中的节点缺乏顺序性或缺乏位置顺序性。我们只有的是节点的索引值，也就是对匹配它们的信息来说是不足够的。那我们如何去设计模组匹配来令它对节点重新参数化是有不变性的?就是了，如果我们有一个图形和其中一个节点有任意的索引值，比如说是6，那这个索引值也可以是122，所以模组匹配必须是独立于节点的索引值。

最简单的做法是只用一个模组向量$w^l$，而不是用$w_{j1}$或$w_{j2}$﹑ $w_{j3}$更多。所以我们匹配这个向量wl对其它在我们图形上的特征。今天的大部份的图形神经网络都是用这个属性。

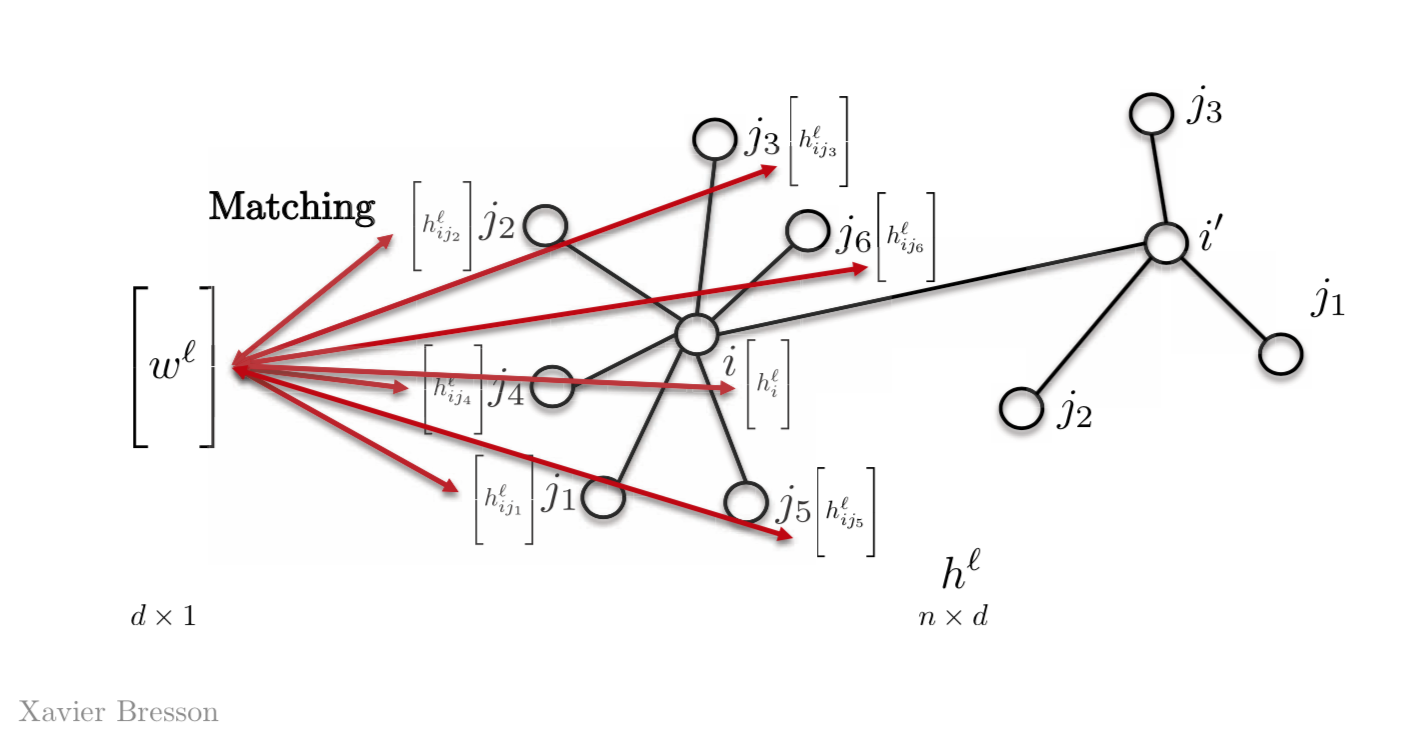
图2: 模组匹配(template matching)用一个模组向量

数学性来说，如果是一个特征的话，我们有，

这里，$w^l$是在尺寸为$d \times 1$的$l$层的模组向量，而 $h_{ij}^l$是在节点j的向量，这个向量尺寸为 $d \times 1$，它会变成在节点$i$的一个标量$h_{i}^{l+1}$。

如果是更多的($d$)特征，

这里，$\boldsymbol{W}^l$尺寸为$d \times d$ ，而且每一个向量性特征，$h_{i}^{l+1}$ 是 $d \times 1$

对于向量表示，

这里，$\boldsymbol{A}$是一个尺寸为$n \times n$的邻接矩阵，而$h^l$是在$l$层的激活函数，它的尺寸为$n \times d$。

基于这个模组匹配的定义，我们可以定义两种空间性的图形卷积网络:各向同性图形卷积网络和各向异性图形卷积网络

各向同性图形卷积网络

基础型空间性图形卷积网络

它的定义和之前一样，但我们在方程式上加上了一个对角矩阵，旁边的数值的平均值。

矩阵表示为

这里， $\boldsymbol{A}$大小为$n \times n$, 而$h^{l}$大小为$n \times d$和$W^{l}$ 大小为$d \times d$，所有东西计算起来为一个大小为$n \times d$ 的$h^{l+1}$矩阵。

而向量的表示是这样，

这里，$h_{i}^{l+1}$的大小为$d \times 1$。

而向量的表示是用来解决节点没有顺序的问题，也就是节点重新参数化的不变性。也就是这样，加一些之前的例子上去，如果节点的数字为6，然后改为122，这对在下一层$h^{l+1}$的激活函数的计算中是不会改变或影响到任何东西的。

我们也可以解决有不同大小的邻域。也就是我们可以有大小为4个节点或10个节点的邻域，这也不会改变或影响到任何东西

先给我们一个设计上的接收视野(Receptive Field)，也就是，以图形神经网路，我们只要考虑那些邻域。

我们有权重分享，也就是我们在所有的特征上都用同样的Wl矩阵，无论是在图形中的位置是什么，也就是卷积层属性。

这个方程式是独立于图形大小，那是因为所有的运算都是本地性运行。

因为这是各向同性模型，邻域会有同样$\boldsymbol{W}^{l}$ 矩阵。

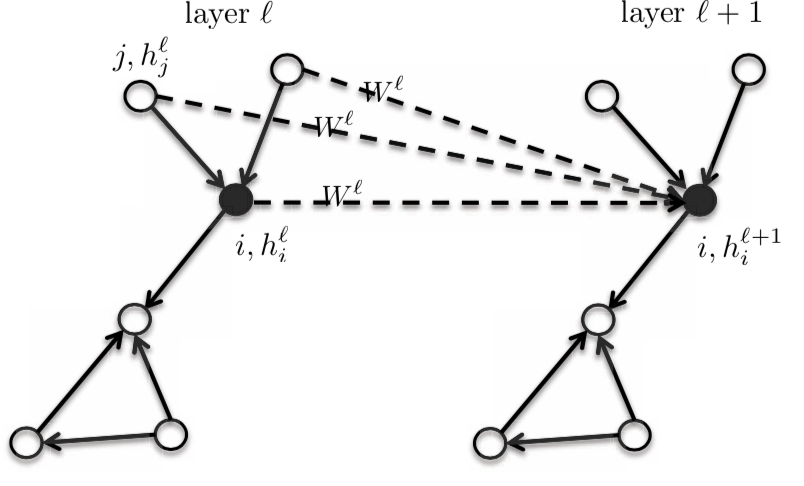
图3: 各向同性模型

So, the activation of the next layer $h_{i}^{l+1}$ is a function of the activation of the previous layer $h_{i}^{l}$ at node $i$ and the neighbourhood of $i$. When we change the function, we get an entire family of graphs. 所以，下一层$h_{i}^{l+1}$的这个激活是…，就是在节点$i$和节点$i$的邻域的之前那一层$h_{i}^{l}$的激活的函数。当我们去改变这个函数时，我们就有整个图形的家族

切布网络(ChebNets)和基础式空间性图形卷积网络(Vanilla Spatial GCNs)

上方定义了基础型空间性图形卷积网络是一个简化了的切布网络。我们可以把切布网络的方程展开截断起来，方法是利用第一和第二切比雪夫函数来得到这个，

图形取样和聚合框架 (Graph SAmple and aggregate, 简称GraphSAGE)

如果边条是在基础型空间性图形卷积网络，那这个邻接矩阵的$\boldsymbol{A}_{ij} = 1$，我们就有个:

\(h_{i}^{l+1} = \eta\bigg(\frac{1}{d_{i}}\sum_{j \in N_{i}}\boldsymbol{W}^{l}h_{j}^{l}\bigg)\) 以这个方程，我们有中央式或核心性的顶点$i$，和这个它的邻域有同样的模板权重(template weight)，为$\boldsymbol{W}^{l}$.。我们可以把它区分起来，方法是给它一个中央性的节点$\boldsymbol{W}_{1}^{l}$，而且有一个不同的模板节点$\boldsymbol{W}_{2}^{l}$和用它在独热邻域中。这会大量提高GNN的效能。这个模型还是本质上被认为是各向同性，那是因为邻域都有同样的权重。

这里，wl1和wl2的大小为dxd，而hli和hlj的大小为dx1。

在这个方程，我们可以找到$\boldsymbol{W}_{2}^{l} h_{j}^{l}$的总和和最大数值，或$h_{j}^{l}$的长短期记忆，而不是平均值。

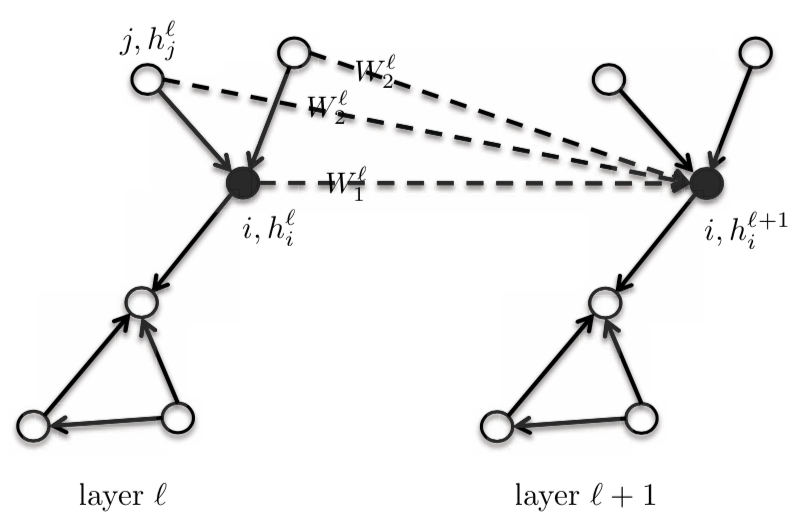
图4: 图形取样和聚合框架 (Graph SAmple and aggregate, 简称GraphSAGE)

图形同构网络(GIN)

一个架构可以区分不是同构的图形们。同构是图形们之间的相等度。在下方的图，两个图形是被认为同构的。同构图形们会被以相似的方式对待，而且不是同构的图形们会被以不相似的方式对待。

图形同构网络是一个图形同构图形卷积网络。

这里，$\texttt{BN}$意思是批量归一化

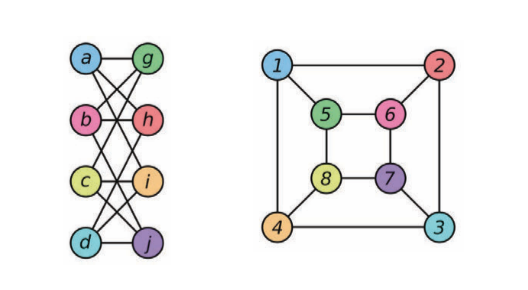
图5: 两个同构图形的例子 ## [各向异性图形卷积网络](https://www.youtube.com/watch?v=Iiv9R6BjxHM&list=PLLHTzKZzVU9eaEyErdV26ikyolxOsz6mq&index=24&t=5586s) 标准的卷积网络有一个能力就是生成各向异性过滤器...也就是说它一个可以注意方向性的东西。这是因为方向性结构是基于上下左。相反，图形卷积网络上方被形容为没卜方向性，而所以这只可以生成各向同性过滤器。各向異性可以自然地以一些邊緣特徵來實作出來。比如，分子就有单键和双键﹑三键。图形地上来说，它是用边的信息来实作出来。 ### Mo网络(MoNets) Mo网络用图形的度数来学习高斯混合模型(Gaussian Mixture Model，英文简称GMM)的参数
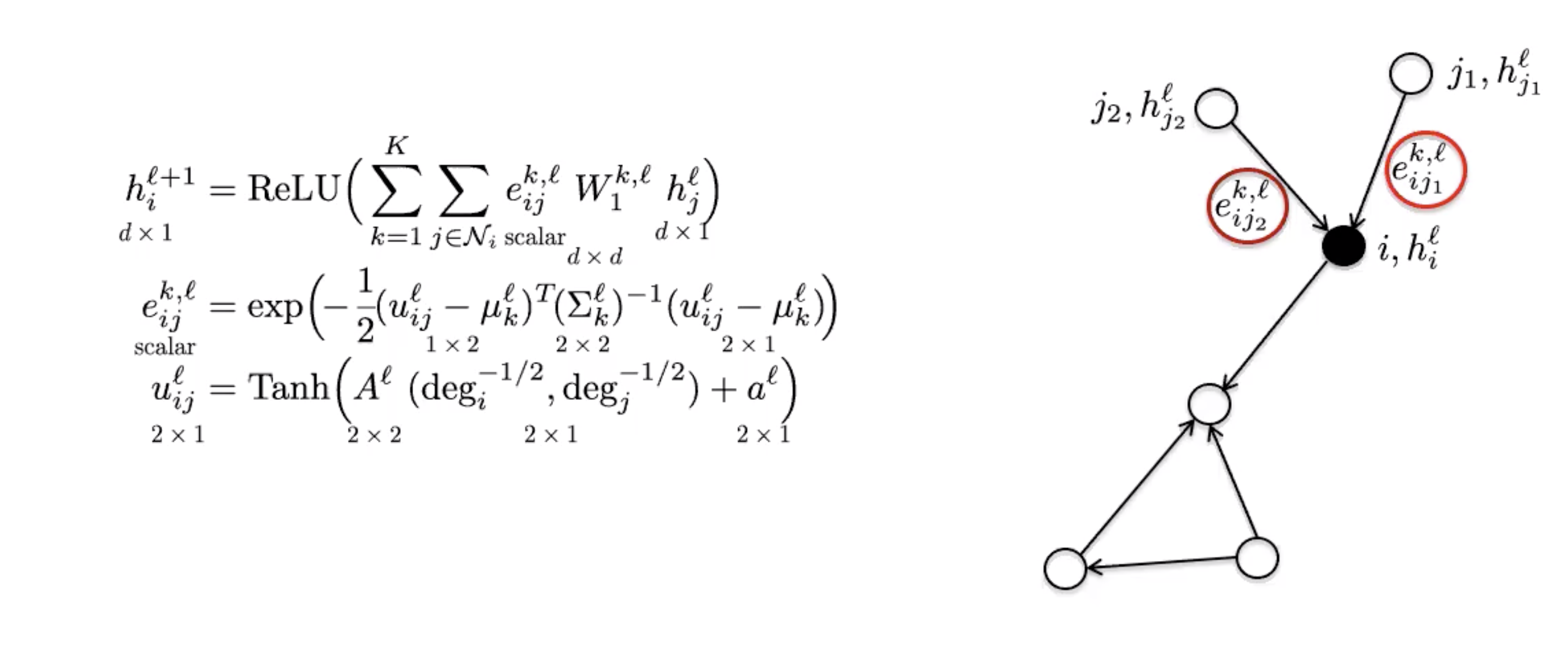
图6： Mo网络 ### 图形注意机制网络(Graph Attention Networks ，简称GAT) 图形注意机制网络使用注意机制来在邻域聚合函数(neighbourhood aggregation function)中实作各向异性。
图7: 图形注意机制网络(Graph Attention Networks ，简称GAT) ### 门控式图形卷积网络 这些都用了一个简单的「边门控式机制」，也可以看得出一个较软的注意力机制过程是如一个在GAT中用上的稀疏注意力机制。
图8: 门控式图形卷积网络 ### 图形变压器(Graph Transformers)
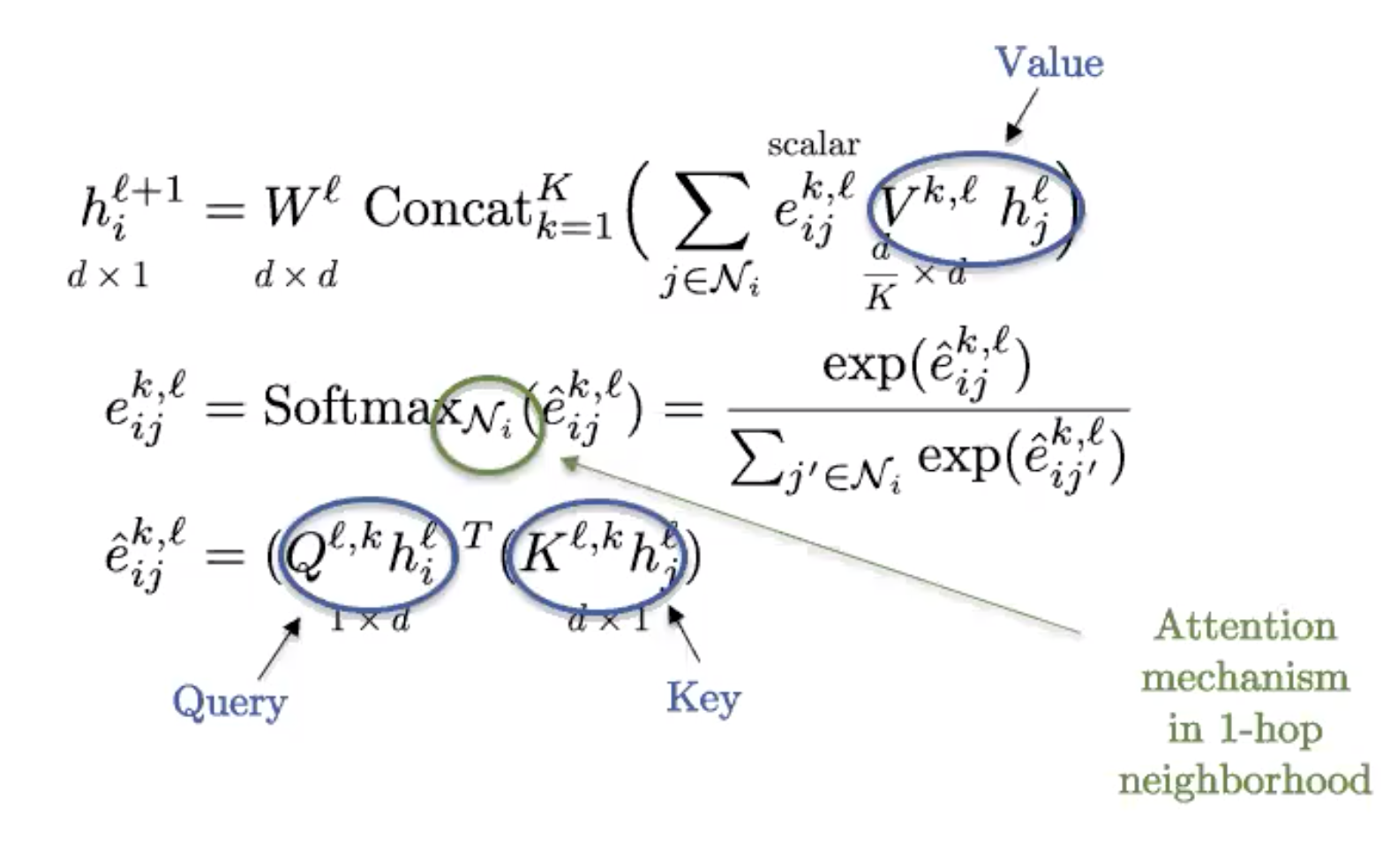
图9: 图形变压器(Graph Transformers) 這個圖形版本是一個基本形變壓器，一般都被用在NLP。如果圖片是完全地連接起來，也就是每兩個節點們分享一條邊，我們會補充一點標準變壓器的定義。 圖形在稀疏性中取得它自身的結構，所以完全連結起來的圖形有一個不重要的的結構和本身是本質地上是一個**集**。變壓器之後是被看成一個「集」神經網絡，而且事實上現在最好的技術就是去分析這些集或一堆特徵。 ## 基準化分析法圖形神經網絡(Benchmarking GNNs) 基準化分析法是任何領域中的過程中，都是十分重要的部份。而最近發佈出的基準，也就是[基準化分析法圖形神經網絡](https://arxiv.org/pdf/2003.00982.pdf/)有6個中規模大小的數據集，這些數據集可以被用在4個基本的圖形問題:圖形分類和圖片回歸﹑節點分類丶邊分類。雖然這些數據集都是中規模大小，但已經足夠來用在不同的圖形神經網絡們。 就如一個**图形回归任務**的例子，我們會去預測出分子溶解度。
图10: 图形回归任务 - 量子化学
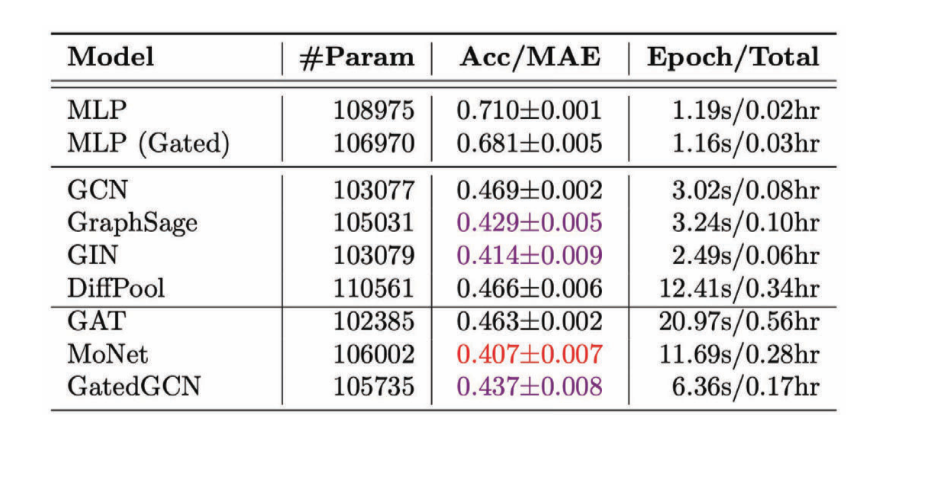
Figure 11: Performance of various GCNs on the regression task 图11：</ b>各种GCN在回归任务上的表现 </center> 我们可以注意到大部例子中，各向异性的图形卷积网络效能比各向同性的图形卷积网络好，因为我们用了方向性属性。 在**图形分类任务**中，如果是决定在用在一个计算机视觉问题上，那是先决在我们在图片中有一些起节点，而我们也想去分类图片。
图 12: 图形分类任务
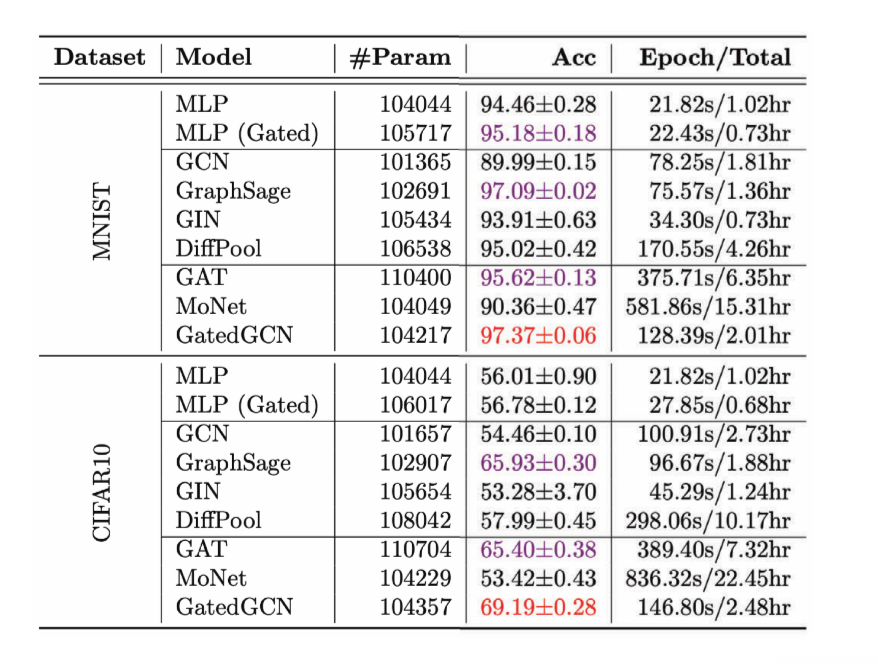
图 13: 不同的圖形卷積神網絡在圖形分類上的效能 **在「邊」分類任務**上，我們有考慮過旅行推銷員的組合優化問題(Combinatorial Optimization problem of the Travelling Salesman Problem ，簡稱TSP)，這裡我們想要知道的是，如果特定的邊是屬於最佳解決方案的話，我們想要知道。如果是屬於解決方案的話，它就屬於第1類，不是就屬於第0類。這裡我們要明確的「邊」的特徵，而且最得最好的只有門控式圖形卷積神網絡。
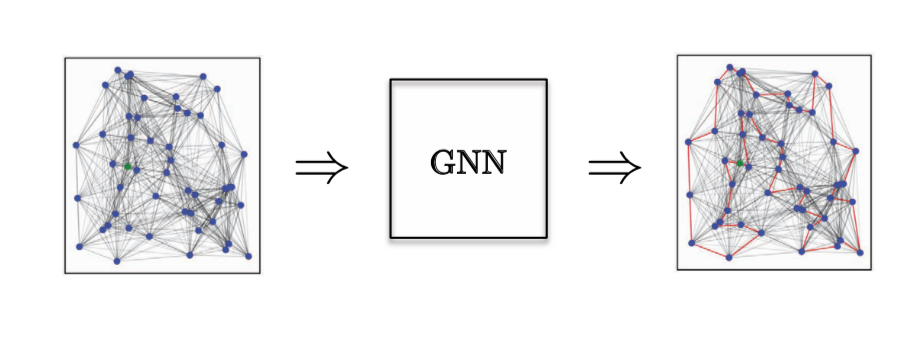
图14:分类「边」的任务。
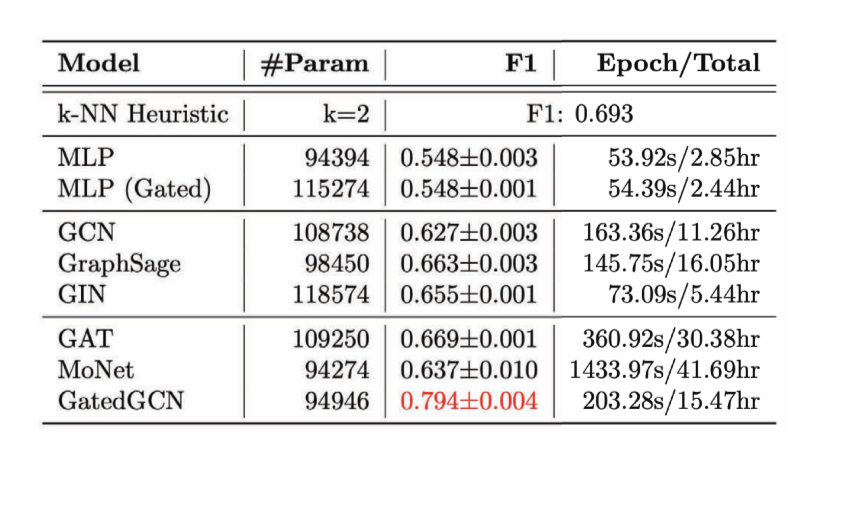
图15: 不同的图形卷积网络的效能 我们可以在自我监督的任务中用上图形卷积网络，它们不会被限于监督学习模型。根据杨立昆 (Yann LeCun)博士，大部份的自我监督学习任务都利用一些图形结构。当我们在文字数据上用上自我监督学习任务时，我们就是用一序列的文字去学预测出缺失了的文字或预测一些新句子。这里有一个图形结构，它就是一个字是在别的字上在一些距离上出现了多少次。文字会是一个线性图形，而邻旁选择到的东西就会被用来训练一个变压器。在这个对比式训练的个案，我们有两个相似的样本，而且也有两个不一样的，这本质上就是一个相似的图形，也就是两个相似的様本就是连结起来，不相似就不是连结起来。 ## 结论 图形卷积网络广泛到由卷积网络到在图形上的数据。卷积网络运算虽要在图形上重新设计。对模板匹配做这些东西的话就会对空间性图形卷积网络带来提升，而且对光谱图形卷积网络来说就会把它转成空间性图形卷积网络。 虽然后者在稀疏矩阵乘法中还没被优化好，但这是对稀疏图形和GPU实作来说是一个线性复杂度。它所有的应用就在下方所示。
图16：应用