Graph Convolutional Networks I

传统卷积神经网络

卷积神经网络是解决高维学习问题的强大结构。

什么是维度诅咒？

考虑一个1024 x 1024像素的图像。该图像可以看作是1,000,000维空间中的一个点。每个维度使用10个样本将生成${10}^{1,000,000}$个图像，这是非常多的。卷积神经网络具有强大的功能，可以很好地提取高维图像数据的表示，例如本示例。

• 维度（图片） = 1024 x 1024 = ${10}^{6}$
• 每个维度取 N = 10 个样本 –> ${10}^{1,000,000}$ 点

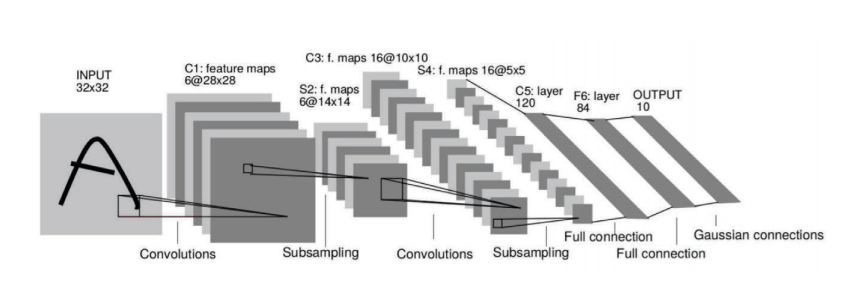
Fig. 1: 图1：卷积神经网络提取高维图像数据的表示形式。

有关卷积神经网络的主要假设：:

1. 数据（图像，视频，语音）是由更小的部分组合的。

它由有以下特征的模式组成：

• 局部性 神经网络中的神经元A仅连接到相邻的层，而不连接到网络中的所有层。我们称其为本地接收场假设。
• 固定性 我们有一些在我们的图像域中共享的相似的模式。例如，图2中间图像中的黄色床单。
• 分层性 低层特征将被组合形成中层特征。随后，这些中层特征将组合起来，逐渐形成更高级别的特征。例如，视觉表示。

Fig. 2: 数据是由更小的结构组合的。

2. 卷积神经网络利用由更小部分组合而成这一结构。

他们提取结构特征并将其提供给分类器，推荐器等。

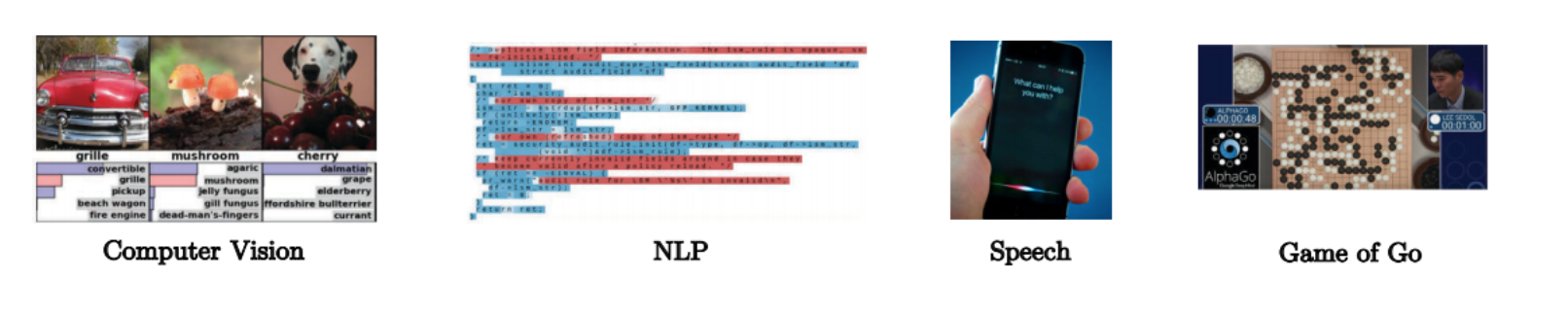
Fig. 3: 卷积神经网络利用由更小部分组合而成这一结构。

图域

数据域

• 图像，体积，视频分别在2D，3D，2D + 1欧几里德域（网格）上。每个像素由红色，绿色和蓝色的向量表示。

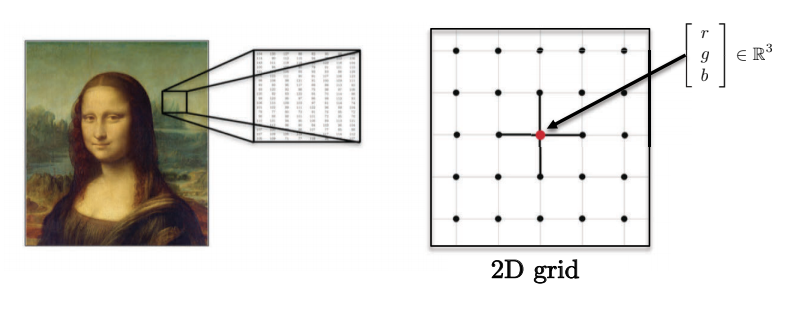
Fig. 4: 图像具有多个维度。

• 句子，单词，语音在一维欧几里得域上。例如，每个字符都可以用整数表示。

  
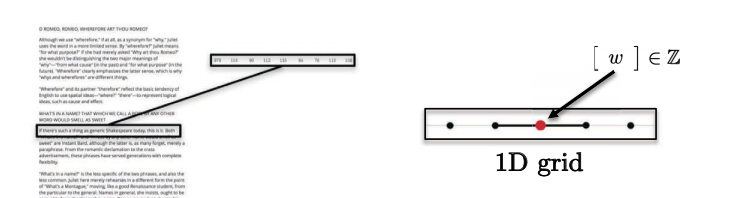
  Fig. 5: 序列是一维的。

• 这些域具有明显的规则空间结构，所以卷积神经网络的操作可以快速进行且在数学上规范定义。

  
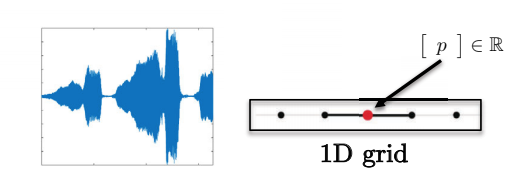
  Fig. 6: 语音数据具有一维网格。

图域

图域的启发性示例

让我们考虑一个社交网络。由于两个用户之间的成对连接不会形成网格，因此最好通过图形表示社交网络。图的节点表示用户，而两个节点之间的边表示两个节点（用户）之间的连接。每个用户都有一个三维特征矩阵，其中包含消息，图像和视频等。

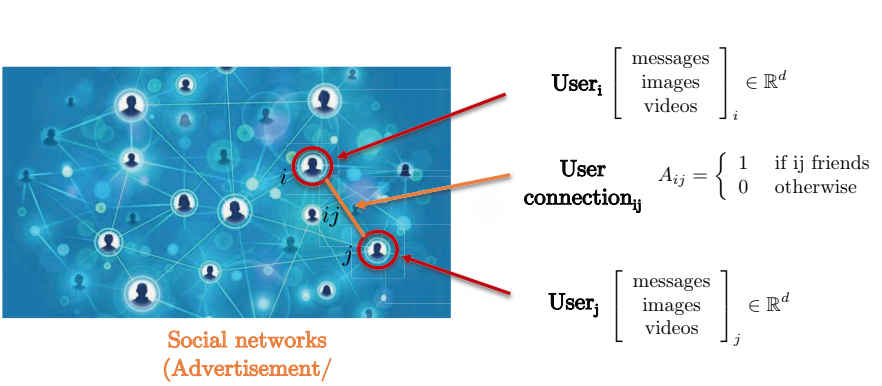
Fig. 7: 通过图表示的社交网络。

用大脑结构与功能之间的联系预测神经遗传疾病就是一个值得考虑的动机示例。如下所示，大脑由几个感兴趣区域（ROI）组成。这些ROI仅局部连接到周围的某些感兴趣区域。邻接矩阵表示感兴趣的不同区域之间的强度。

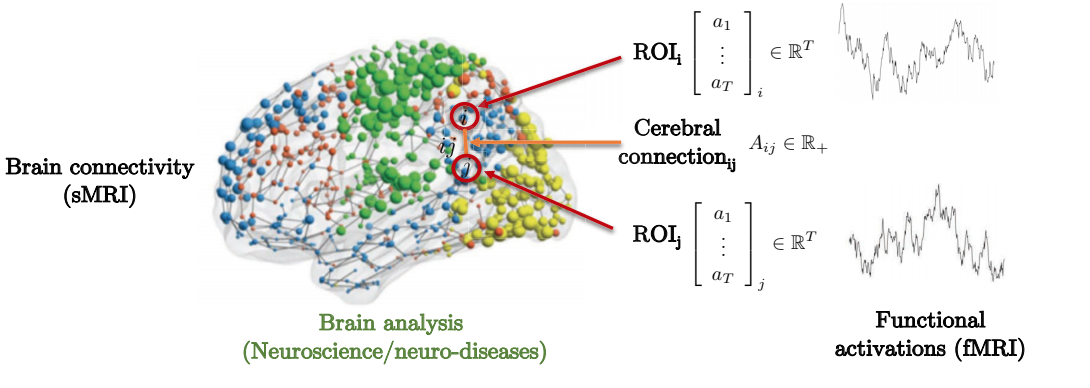
Fig. 8: 通过图形表示的大脑连通性。

量子化学也提供了图形域的有趣表示。每个原子由图中的一个节点表示，并通过使用边代表键与其他原子连接。这些分子/原子中的每一个都具有不同的特征，例如带电荷，键类型等。

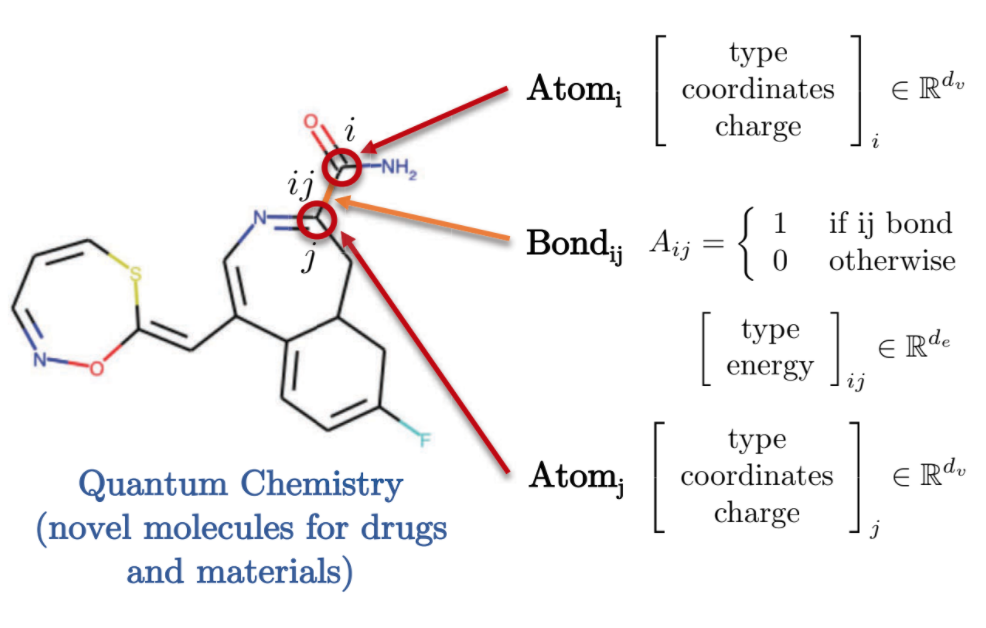
Fig. 9: 通过图表示的量子化学。

图的定义和特征

*图G由以下项定义： * 顶点 V * 边 E * 邻接矩阵 A

• 图的特征:
  • 点特征: $h_{i}$, $h_{j}$ (原子类型)
  • 边特征: $e_{ij}$ (键类型)
  • 图特征: g (分子能)

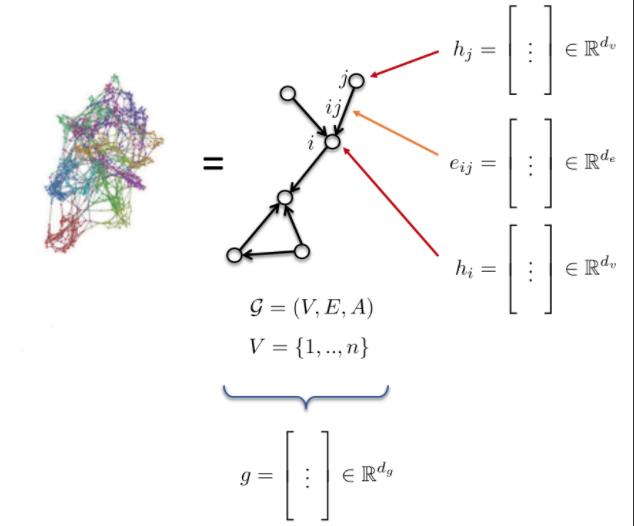
Fig. 10: 图。

传统卷积网络中的卷积

卷积

我们简单把卷积定义为：

\(h^{\ell+l} = w^\ell * h^\ell,\) 其中 $h^{\ell+1}$ 是 $n_1\times n_2\times d$维的, $w^\ell$ 是 $3\times 3\times d$维的, 而 $h^\ell$ 是 $n_1\times n_2\times d$维的. 例如, $n_1$ 和 $n_2$ 可以分别是图像的$x$ 和$y$方向上的像素数, 而d是每个像素的维度（例如，彩色图像像素维度为3）。

因此, $h^{\ell+1}$ 是通过对第 $(\ell+1)$-th 层的一个特征应用卷积 $w^\ell$生成的第$\ell$-th 个隐藏层的一个特征。
通常，内核比较小，用以表示本地接收字段–-在这种情况下为$3\times 3$ , 或 $5\times 5$。
注意：我们使用填充来确保 $h^{\ell+1}$ 的维度与$h^\ell$的相同。\

例如，在此图像中，内核可用于识别线。

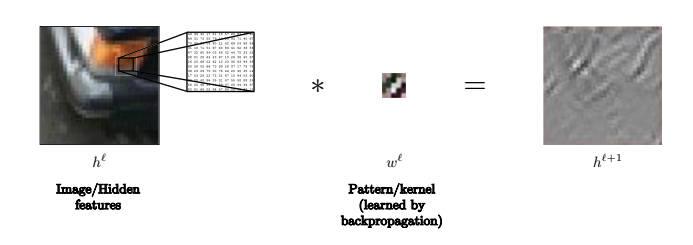
Fig. 11: 内核可用于识别图像中的线条。

我们如何定义卷积？

更确切地说，卷积定义如下：

上面将卷积定义为模板匹配。
我们通常使用$h_{i+j}$代替$h_{i-j}$，因为前者实际上是相关性，更像模板匹配。但是，使用第一个还是第二个表发方法并不重要，因为您的内核只是被翻转了，这不会影响模型学习。 在第三行中，我们将$h_{i+j}^\ell$写为$h_{ij}^\ell$。 内核非常小，因此我们没有像第二行那样对整个图像$\Omega$求和，而只是对像元$i$的邻域$\mathcal{N}_i$求和，如第三行所示。

这使得卷积的复杂度为$O(n)$，其中$n$是输入图像中的像素数。

卷积正是针对$n$个像素中的每个像素，对$3\times 3$ 格上的$d$维向量的内积求和。

因此，复杂度为$n\cdot 3\cdot 3\cdot d$，即$O(n)$；而且，可以与n个像素中的每个像素进行GPU并行计算。

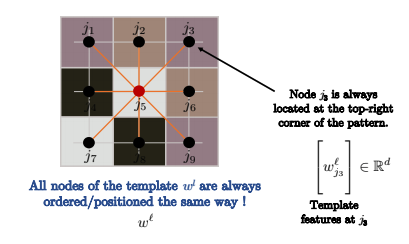
Fig. 12: 节点以相同的方式排序。

如果要卷积的图形是网格（比如计算机视觉中对图像进行标准卷积一样），则节点的排列方式如上图所示。因此，$j_3$将始终位于模式的右上角。

对于下图中的所有节点$i$，例如$i$和$i’$，内核的节点顺序始终是相同的。例如，您总是将模式右上角的$j_3$与图像局部（我们对像素$i$进行卷积的局部小块）的右上角进行比较，如下所示。 从数学上讲：

和

始终位于模板和图像补丁之间的右上角。

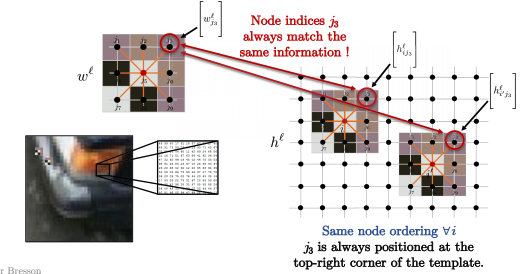
Fig. 13: 图像局部小块与模板匹配。

我们可以把模板匹配延伸到图吗？

我们有几个需要考虑的问题：

1. 首先，在图中，节点没有排序。

因此，在下图所示的模板中，节点$j_3$没有特定位置，只有一个（不具备实际意义的）索引。因此，当我们尝试与下图中的节点$i$和$i’$匹配时，我们不知道j_3是否在两个卷积中与相同节点匹配。 这是因为没有图形的右上角概念。没有上，下，左，右的概念。 因此，模板匹配实际上没有任何意义，如上所述，我们不能直接按照模板匹配的定义来应用它（上图）。

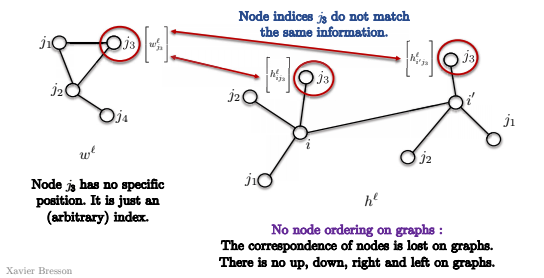
Fig. 14: 图中没有节点顺序。

1. 第二个问题是邻域的大小可能不同。

下面图中显示的模板$w^\ell$有4个节点，但是节点$i$附近有7个节点。 我们如何比较这两个节点呢？

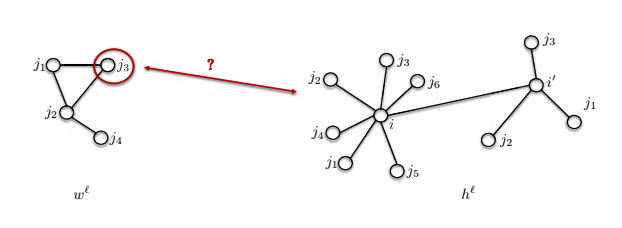
Fig. 15: 图中不同的邻域大小。

图卷积

现在，我们使用卷积定理为图定义卷积。

卷积定理指出，两个函数的卷积的傅立叶变换是它们的傅立叶变换的点积：

\(\mathcal{F}(w*h) = \mathcal{F}(w) \odot \mathcal{F}(h) \implies w * h = \mathcal{F}^{-1}(\mathcal{F}(w)\odot\mathcal{F}(h))\) 通常，傅立叶变换具有 $O(n^2)$ 复杂度，但是如果域是网格，则可以通过FFT将复杂度降低为$O(n\log n)$。

###我们可以将卷积定理扩展到图吗？ 这引出了两个问题： 1.如何为图定义傅立叶变换？ 2.如何计算紧凑内核$O（n）$时间的快速频谱卷积（如模板匹配中）？

我们将对图形神经网络使用这两种设计：模板匹配将用于空间图卷积网络，卷积定理将用于频谱卷积网络。

光谱图卷积网络

如何进行频谱卷积？

步骤 1 : 图拉普拉斯

这是频谱图理论中的核心运算。

定义

注意矩阵$A$是邻接矩阵，而$\Delta$是拉普拉斯算子，它等于单位矩阵减去由矩阵$D$归一化的邻接矩阵。$D$是对角矩阵，对角线上的每个元素都是节点的度数。这叫标准化的拉普拉斯算子或默认的拉普拉斯算子。 拉普拉斯算子可以解释为图的平滑度的度量，换句话说，就是局部值$h_i$和其邻域平均值$h_j$的差。以下公式中的$d_i$是节点$i$的度数，$\mathcal{N}_{i}$是节点$i$的所有邻居。

上面的公式是将Laplacian应用于节点$i$上的函数$h$，即$h_i$的值减去其相邻节点$h_j$的平均值。基本上，如果信号非常平滑，则拉普拉斯值很小，反之亦然。

步骤2：傅立叶函数

以下是图拉普拉斯算子的本征分解，

拉普拉斯算子分解为三个矩阵, $\Phi ^ T$, $\Lambda$, $\Phi$.

$\Phi$ 定义如下,它包含列向量或Lap特征向量 $\phi_1$ 至$\phi_n$，每个向量的大小为$n \times 1$，它们也称为傅里叶函数。傅立叶函数构成正交的基础。

其中 \(\begin{array}{l}\text { where } \underset{n \times n}{\Delta}\Phi=\left[\phi_{1}, \ldots, \phi_{n}\right]=\text { and } \Phi^{T} \Phi=\mathrm{I},\left\langle\phi_{k}, \phi_{k^{\prime}}\right\rangle=\delta_{k k^{\prime}} \\\end{array}\)

$\Lambda$是具有拉普拉斯特征值的对角矩阵，对角线上是$\lambda_1$至$\lambda_n$。从规范化应用来看，这些值通常在$0$到$2$的范围内。这些值也称为图的频谱。请参阅下面的公式。 \(\begin{array}{c}\text { where } \underset{n \times n}\Lambda=\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{n}\right) \text { and } 0 \leq \lambda_{1} \leq \ldots \leq \lambda_{n}=\lambda_{\max } \leq 2\end{array}\)

以下是研究特征值分解的示例。拉普拉斯矩阵$\Lambda$与特征向量$\phi_k$相乘，结果的形状为$n \times 1$，结果为$\lambda_k \phi_k$。

下图是一维欧几里得拉普拉斯特征向量的可视化。

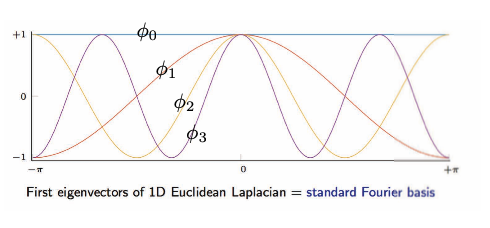
Fig. 16: 网格/欧式域一维欧式拉普拉斯算子的特征向量。

对于图域，从左到右是图的第一，第二，第三，…傅立叶函数。$\phi_1$具有正（红色）和负（蓝色）值的振荡，与ϕ_2，ϕ_3$\phi2$, $\phi3$也有。这些振荡取决于图的拓扑，而拓扑与图的几何形状（例如社区，枢纽等）有关，这有助于图聚类。见下文。

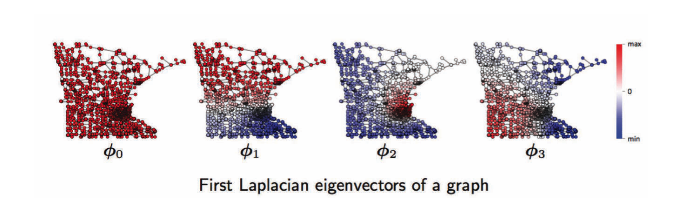
Fig. 17:图域：图的傅立叶函数。

第三步：傅立叶变换

\(\begin{aligned} \underset{n \times 1} h &=\sum_{k=1}^{n} \underbrace{\left\langle\phi_{k}, h\right\rangle}_{\mathcal{F}(h)_{k}=\hat{h}_{k}=\phi_{k}^{T} h}\underset{n \times 1}{\phi_{k}} \\ &=\sum_{k=1}^{n} \hat{h}_{k} \phi_{k} \\ &=\underbrace{\Phi \hat{h}}_{ \mathcal{F}^{-1}(\hat{h}) } \end{aligned}\) 傅里叶级数：用傅里叶函数分解函数h。

取函数h并投影到每个傅立叶函数ϕ_k上，得到k的傅立叶级数的系数（一个标量），然后乘以函数ϕ_k。傅立叶变换基本上可以视为在傅立叶函数上投影一个函数h，结果是傅立叶级数的系数。

傅立叶变换/傅立叶级数的系数

傅里叶级数：用傅里叶函数分解函数h。 取函数$h$并投影到每个傅立叶函数$\phi_k$上，得到$k$的傅立叶级数的系数（一个标量），然后乘以函数$\phi_k$。 傅立叶变换基本上可以视为在傅立叶函数上投影一个函数$h$，结果是傅立叶级数的系数。

傅立叶变换/傅立叶级数的系数

傅立叶变换/傅立叶级数的系数

傅里叶变换是线性运算，将矩阵$\Phi^{T}$与向量$h$相乘。

步骤4：卷积定理

两个函数的卷积的傅立叶变换是它们的傅立叶变换的点积。 \(\begin{aligned} \underset{n \times 1} {w * h} &=\underbrace{\mathcal{F}^{-1}}_{\Phi}(\underbrace{\mathcal{F}(w)}_{\Phi^{T} w=\hat{w}} \odot \underbrace{\mathcal{F}(h)}_{\Phi^{T} h}) \\ &=\underset{n \times n}{\Phi}\left( \underset{n \times 1}{\hat{w}}\odot \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi\left(\underset{n \times n}{\hat{w}(\Lambda)} \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi \hat{w}(\Lambda) \Phi^{T} h \\ &=\hat{w}(\underbrace{\Phi \Lambda \Phi^{T}}_{\Delta}) h \\ &=\underset{n \times n}{\hat{w}(\Delta)} \underset{n \times1}h \\ & \end{aligned}\)

上面的示例是$w$和$h$的卷积，形状均为$n \times 1$，它等于$w$ 和$h$的傅立叶变换之间的点积的傅立叶变换的逆。上面的公式表明，它也等于$\hat{w}(\Delta)$和 $h$的矩阵乘积。

图$h$和$w$ 上两个函数的卷积是取w的谱函数并将其应用到拉普拉斯并乘以$h$，这就是谱卷积的定义。但是，计算复杂度为$\mathrm{O}\left(n^{2}\right)$，$n$是图中的节点数。

局限性

图域的谱卷积不具平移不变性，这意味着如果平移，函数的形状也可能会更改，而在网格/欧氏域中则不会。

推荐书目

Spectral graph theory, Fan Chung, (谐波分析，图论，组合问题，优化)