注意力机制和Transformer

注意力机制

在讨论Transformer架构之前，我们先介绍注意的概念。 注意力主要有两种类型：自我注意力vs.交叉注意力，在这些类别中，我们可以比较硬vs.软注意力。

稍后我们将看到，转换器由注意力模块组成，注意力模块是集合之间的映射，而不是序列之间的映射，这意味着我们不对输入/输出强加排序。

自我注意力 (I)

考虑一组$ t $输入$ \ boldsymbol {x} $：

其中每个 $\boldsymbol{x}_i$是一个$n$维向量. 由于集合具有$ t $个元素，每个元素都属于$ \ mathbb {R} ^ n $，因此我们可以将集合表示为矩阵$ \ boldsymbol {X} \ in \ mathbb {R} ^ {n \ times t} $。

通过自我注意，隐藏表示$ h $是输入的线性组合： \(\boldsymbol{h} = \alpha_1 \boldsymbol{x}_1 + \alpha_2 \boldsymbol{x}_2 + \cdots + \alpha_t \boldsymbol{x}_t\)

使用上述矩阵表示形式，我们可以将隐藏层写为矩阵乘积：

其中$\boldsymbol{a} \in \mathbb{R}^t$ 是具有$\alpha_i$分量的列向量.

请注意，这与我们到目前为止看到的隐藏表示形式不同，在隐藏表示形式中，输入乘以权重矩阵。

根据我们施加在向量$ \ vect {a} $上的约束，我们可以获得硬或软的注意力。

硬注意力

格外注意，我们对alpha施加了以下约束：$ \ Vert \ vect {a} \ Vert_0 = 1 $。 这意味着$ \ vect {a} $是一个热门向量。 因此，输入的线性组合中除一个系数外的所有系数都等于零，并且隐藏表示减小为与元素$ \ alpha_i = 1 $相对应的输入$ \ boldsymbol {x} _i $。

软注意力

对于软注意力，我们强加$ \ Vert \ vect {a} \ Vert_1 = 1 $。 隐藏的表示形式是系数总和为1的输入的线性组合。

自我注意力 (II)

$ \ alpha_i $来自哪里？

我们通过以下方式在\ mathbb {R} ^ t $中获得向量$ \ vect {a} \

其中$ \ beta $表示$ \ text {soft（arg）max}（\ cdot）$的逆温度参数。 $ \ boldsymbol {X} ^ {\ top} \ in \ mathbb {R} ^ {t \ times n} $是集合$ \ lbrace \ boldsymbol {x} _i \ rbrace \ _ {i = 1} ^ t $，而$ \ boldsymbol {x} $代表集合中的通用$ \ boldsymbol {x} _i $。 请注意，$ X ^ {\ top} $的第$ j $行对应于元素$ \ boldsymbol {x} _j \ in \ mathbb {R} ^ n $，因此$$的$ j $行 \ boldsymbol {X} ^ {\ top} \ boldsymbol {x} $是$ \ boldsymbol {x} _j $与$ \ lbrace中每个$ \ boldsymbol {x} _i $的标量乘积\ bracesymbol {x} _i \ rbrace \ _ {i = 1} ^ t $。

向量$ \ vect {a} $的分量也称为“分数”，因为两个向量之间的标量积告诉我们两个向量的对齐方式或相似程度。因此，$ \ vect {a} $的元素提供有关整个集合与特定$ \ boldsymbol {x} _i $的相似性的信息。

方括号代表可选参数。请注意，如果使用$ \ arg \ max（\ cdot）$，我们将获得一个很热的alpha向量，这引起了大家的注意。另一方面，$ \ text {soft（arg）max}（\ cdot）$引起柔和的注意。在每种情况下，所得向量$ \ vect {a} $的分量总和为1。

这样生成$ \ vect {a} $可以得到一组，每个$ \ boldsymbol {x} _i $一个。此外，每个$ \ vect {a} _i \位于\ mathbb {R} ^ t $中，因此我们可以将alphas堆叠在矩阵$ \ boldsymbol {A} \中\ mathbb {R} ^ {t \ times t} $中。

由于每个隐藏状态都是输入$ \ boldsymbol {X} $和向量$ \ vect {a} $的线性组合，因此我们获得了一组$ t $隐藏状态，可以将它们堆叠成矩阵$ \ boldsymbol {H} \ in \ mathbb {R} ^ {n \ times t} $。

高性能键-值存储

键值存储是用于存储（保存），检索（查询）和管理关联数组（字典/哈希表）的范例。

例如，假设我们想找到一种制作千层面的食谱。 我们有一本食谱书，然后搜索“烤宽面条”-这是查询。 将对照您数据集中的所有可能键检查此查询-在这种情况下，这可能是书中所有食谱的标题。 我们检查查询与每个标题的对齐程度，以找到查询与所有各个键之间的最大匹配分数。 如果我们的输出是argmax函数-我们检索得分最高的单个配方。 否则，如果我们使用软的argmax函数，我们将获得概率分布，并且可以按顺序从最相似的内容检索到越来越少与查询匹配的配方。

基本上，查询就是问题。 给定一个查询，我们针对每个键检查该查询并检索所有匹配的内容。

查询，键和值

每个向量$ \ vect {q}，\ vect {k}，\ vect {v} $都可以简单地视为特定输入$ \ vect {x} $的旋转。 其中$ \ vect {q} $只是$ \ vect {x} $旋转了$ \ vect {W_q} $，而$ \ vect {k} $只是$ \ vect {x} $旋转了$ \ vect {W_k } $，以及类似的$ \ vect {v} $。 请注意，这是我们第一次引入“可学习的”参数。 由于注意力完全基于方向，因此我们也不包括任何非线性。

为了将查询与所有可能的键进行比较，$ \ vect {q} $和$ \ vect {k} $必须具有相同的维数，即* ie * $ \ vect {q}，\ vect {k} \ in \ mathbb {R} ^ {d’} $。

但是，$ \ vect {v} $可以是任何维度。 如果继续我们的千层面食谱示例-我们需要查询以维度作为关键字，即*，即我们正在搜索的不同食谱的标题。 但是，检索到的相应配方的尺寸$ \ vect {v} $可以任意长。 因此我们在\ mathbb {R} ^ {d’’} $中有$ \ vect {v} \。

为简单起见，在此我们假设所有元素的维数均为$ d $，即

所以现在我们有了一组$ \ vect {x} $，一组查询，一组键和一组值。 由于我们堆叠了$ t $个向量，因此我们可以将这些集合堆叠到每个具有$ t $列的矩阵中。 每个向量的高度为$ d $。 \(\{ \vect{x}_i \}_{i=1}^t \rightsquigarrow \{ \vect{q}_i \}_{i=1}^t, \, \{ \vect{k}_i \}_{i=1}^t, \, \, \{ \vect{v}_i \}_{i=1}^t \rightsquigarrow \vect{Q}, \vect{K}, \vect{V} \in \mathbb{R}^{d \times t}\)

我们将一个查询$ \ vect {q} $与所有键$ \ vect {K} $的矩阵进行比较：

然后，隐藏层将是$ \ vect {V} $的列的线性组合，并由$ \ vect {a} $中的系数加权：

由于我们有$ t $个查询，因此我们将获得$ t $个对应的$ \ vect {a} $权重，因此将得到一个维度为$ t \ times t $的矩阵$ \ vect {A} $。

因此在矩阵式中我们有:

顺便说一句，我们通常将$ \ beta $设置为：

这样做是为了使温度在不同尺寸的$ d $的选择中保持恒定，因此我们将其除以尺寸$ d $的平方根。 （想想向量$ \ vect {1} \ in \ R ^ d $的长度是多少。）

为了实现，我们可以通过将所有$ \ vect {W} $堆叠到一个高$ \ vect {W} $中，然后计算$ \ vect {q}，\ vect {k}，\ vect { v} $：

还有“头”的概念。 上面我们看到了一个带有一个头的示例，但是我们可以有多个头。 例如，假设我们有$ h $头，那么我们有$ h $ $ \ vect {q} $，$ h $ $ \ vect {k} $和$ h $ $ \ vect {v} $ ，最后得到$ \ mathbb {R} ^ {3hd} $中的向量：

但是，我们仍然可以通过在\ mathbb {R} ^ {d \ times hd} $中使用$ \ vect {W_h} \，将多头值转换为原始尺寸$ \ R ^ d $。 这只是实现键值存储的一种可能方法。

The Transformer

现在，特别是在扩展我们的注意力知识的同时，我们将解释transformer的基本组成部分。 特别是，我们将通过一个基本的转换器进行正向传递，并了解如何在标准的编码器-解码器范例中使用注意力并将其与RNN的顺序体系结构进行比较。

编码器-解码器结构

我们应该熟悉这个术语。 在自动编码器演示过程中，它最突出地显示出来，并且是到目前为止的前提条件。 总而言之，输入是通过编码器和解码器馈送的，这些编码器和解码器在数据上施加了某种瓶颈，仅迫使最重要的信息通过。 此信息存储在编码器块的输出中，并可用于各种不相关的任务。

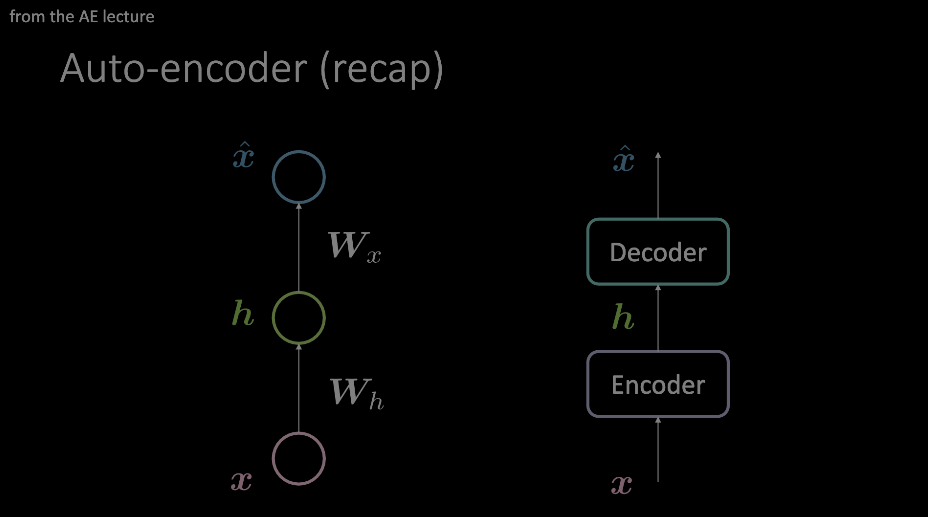
Figure 1: 自编码器的两个示例图。 左侧的模型显示了如何通过两个仿射变换+激活来设计自编码器，其中右侧的图像用任意操作模块替换了单个“层”。

我们的“注意力”吸引到了如右侧模型中所示的自动编码器布局，现在将在变压器的背景下深入了解内部。

编码模块

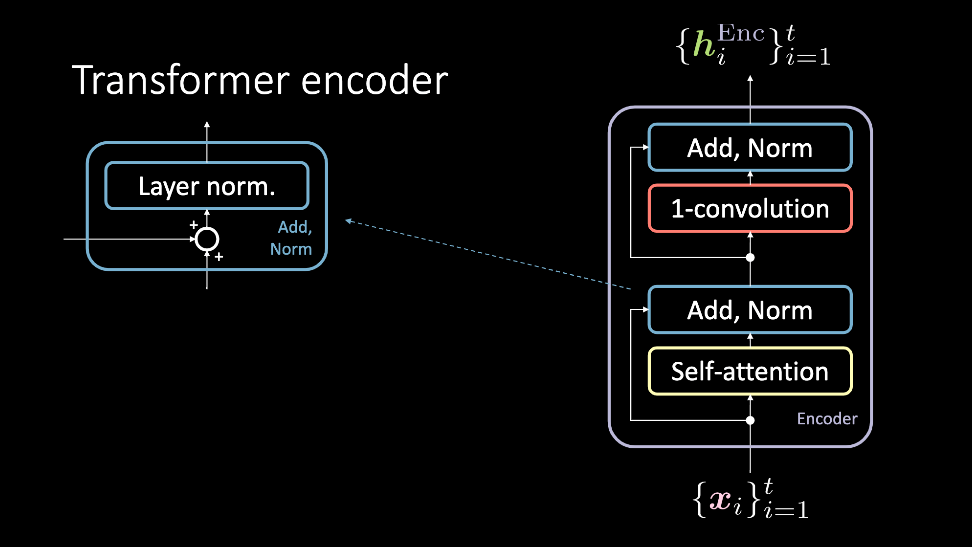
Figure 2: Transformer编码, 它接受一组输入$ \ vect {x} $，并输出一组隐藏表示 $\vect{h}^\text{Enc}$.

编码器模块接受一组输入，这些输入同时通过自我关注模块馈送，并绕过它到达Add, Norm 模块。 在这一点上，它们再次同时通过1D卷积和另一个Add, Norm块，并因此作为隐藏表示集输出。 然后，这组隐藏的表示形式要么通过任意数量的编码器模块（即*更多的层）发送，要么发送到解码器。 现在我们将更详细地讨论这些块。

自我注意力

自我注意模型是简单的注意力模型。 查询，键和值是从顺序输入的同一项生成的。 在尝试为顺序数据建模的任务中，在此输入之前添加位置编码。 该块的输出是注意力加权值。 自我注意块接受一组输入，从$ 1，\ cdots，t $开始，输出$ 1，\ cdots，t $注意加权值，这些值通过编码器的其余部分馈入。

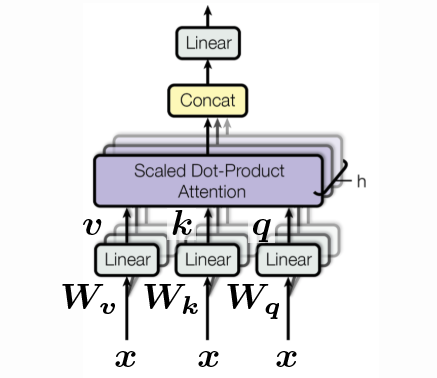
Figure 3: 自我注意块。 输入的顺序在第3维上显示为一组，并进行了串联。

Add, Norm

添加规范块具有两个组件。 首先是add块，这是一个残余连接，并进行层归一化。

1D-卷积

在此步骤之后，将应用一维卷积（也称为位置前馈网络）。 该块由两个密集层组成。 根据设置的值，此块允许您调整输出$ \ vect {h} ^ \ text {Enc} $的尺寸。

解码模块

Tranformer解码器遵循与编码器类似的过程。 但是，还有一个额外的子块要考虑。 此外，此模块的输入是不同的。

Figure 4: 解码器的友好说明。

交叉注意力

交叉注意遵循用于自注意块的查询，键和值设置。 但是，输入要复杂一些。 解码器的输入是数据点$ \ vect {y} \ _ i $，然后将其传递给自注意并添加范数块，最后到达交叉注意块。 这用作交叉注意的查询，其中键和值对是输出$ \ vect {h} ^ \ text {Enc} $，其中此输出是使用所有过去的输入$ \ vect {x} \ _ 1来计算的 ，\ cdots，\ vect {x} \ _ {t} $。

总结

集合$ \ vect {x} \ _ 1 $到$ \ vect {x} \ _ {t} $通过编码器输入。 使用自我注意和更多块，获得输出表示$ \ lbrace \ vect {h} ^ \ text {Enc} \ rbrace_ {i = 1} ^ t $，该输出表示被馈送到解码器。 在对其施加自注意力之后，进行交叉注意力。 在此块中，查询与目标语言$ \ vect {y} \ _ i $中的符号表示相对应，并且键和值从源语言语句（$ \ vect {x} \ _ 1 $到$ \ vect {x} \ _ {t} $）。 凭直觉，交叉注意会发现输入序列中的哪些值与构造$ \ vect {y} \ _ t $最相关，因此应获得最高的注意系数。 然后，这个交叉注意力的输出将通过另一个1D卷积子块进行馈送，我们得到$ \ vect {h} ^ \ text {Dec} $。 对于指定的目标语言，可以通过将$ \ lbrace \ vect {h} ^ \ text {Dec} \ rbrace_ {i = 1} ^ t $与某些目标数据进行比较，从此处直接了解培训的开始方式。

单词语言模型

我们在解释transformer最重要的模块之前遗漏了一些重要的事实，但是现在需要讨论它们，以了解transformer如何在语言任务中实现最新的结果。

位置编码

注意机制使我们能够并行化操作并极大地加快了模型的训练时间，但是却丢失了顺序信息。 位置编码功能使我们能够捕获此上下文。

语义表现

在训练transformer的整个过程中，会生成许多隐藏的表示形式。 为了创建类似于PyTorch中的单词模型示例所使用的嵌入空间，交叉注意的输出将提供单词$ x_i $的语义表示，此时可以对此进行进一步的实验。 数据集。

代码总结

现在，我们将以更容易理解的格式（代码）来查看上面讨论的transformer块！

我们将在第一个模块中研究多头注意力模块。 依赖于此块中输入的查询，键和值，它既可以用于自我注意，也可以用于交叉注意。

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, p, d_input=None):
        super().__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        if d_input is None:
            d_xq = d_xk = d_xv = d_model
        else:
            d_xq, d_xk, d_xv = d_input
        # Embedding dimension of model is a multiple of number of heads
        assert d_model % self.num_heads == 0
        self.d_k = d_model // self.num_heads
        # These are still of dimension d_model. To split into number of heads
        self.W_q = nn.Linear(d_xq, d_model, bias=False)
        self.W_k = nn.Linear(d_xk, d_model, bias=False)
        self.W_v = nn.Linear(d_xv, d_model, bias=False)
        # Outputs of all sub-layers need to be of dimension d_model
        self.W_h = nn.Linear(d_model, d_model)

初始化多头注意力类。 如果 d_input 存在, 变成交叉注意力. 否则是自我注意力.查询，键，值设置被构造为输入 d_model的线性变换.

def scaled_dot_product_attention(self, Q, K, V):
    batch_size = Q.size(0)
    k_length = K.size(-2)

    # Scaling by d_k so that the soft(arg)max doesnt saturate
    Q = Q / np.sqrt(self.d_k)  # (bs, n_heads, q_length, dim_per_head)
    scores = torch.matmul(Q, K.transpose(2,3))  # (bs, n_heads, q_length, k_length)

    A = nn_Softargmax(dim=-1)(scores)  # (bs, n_heads, q_length, k_length)

    # Get the weighted average of the values
    H = torch.matmul(A, V)  # (bs, n_heads, q_length, dim_per_head)

    return H, A

在通过关注向量缩放后，返回与值的编码相对应的隐藏层。 为了记录目的（序列中的哪些值被注意掩盖了？），还返回A。

def split_heads(self, x, batch_size):
    return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

将最后一个维度拆分为 (heads × depth). 转置后成 (batch_size × num_heads × seq_length × d_k)

def group_heads(self, x, batch_size):
    return x.transpose(1, 2).contiguous().
        view(batch_size, -1, self.num_heads * self.d_k)

将注意力头集中在一起，以获得与批次大小和序列长度一致的正确形状。

def forward(self, X_q, X_k, X_v):
    batch_size, seq_length, dim = X_q.size()
    # After transforming, split into num_heads
    Q = self.split_heads(self.W_q(X_q), batch_size)
    K = self.split_heads(self.W_k(X_k), batch_size)
    V = self.split_heads(self.W_v(X_v), batch_size)
    # Calculate the attention weights for each of the heads
    H_cat, A = self.scaled_dot_product_attention(Q, K, V)
    # Put all the heads back together by concat
    H_cat = self.group_heads(H_cat, batch_size)  # (bs, q_length, dim)
    # Final linear layer
    H = self.W_h(H_cat)  # (bs, q_length, dim)
    return H, A

多头注意力的前向传播。

给定一个输入，将其分为q，k和v，这时，这些值将通过缩放的点乘积注意机制馈入，连接并馈入最终的线性层。 注意块的最后输出是找到的注意，以及通过其余块传递的隐藏表示。

尽管在变压器/编码器中显示的下一个块是Add，Norm，这是PyTorch中已内置的功能。 这样，它是一个非常简单的实现，不需要它自己的类。 接下来是一维卷积块。 有关更多详细信息，请参阅前面的部分。

现在我们已经构建了所有主类（或为我们构建了所有主类），现在我们转向编码器模块。

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, conv_hidden_dim, p=0.1):
        self.mha = MultiHeadAttention(d_model, num_heads, p)
        self.layernorm1 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)
        self.layernorm2 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)

    def forward(self, x):
        attn_output, _ = self.mha(x, x, x)
        out1 = self.layernorm1(x + attn_output)
        cnn_output = self.cnn(out1)
        out2 = self.layernorm2(out1 + cnn_output)
        return out2

在功能最强大的Transformer中，任意数量的这些编码器相互堆叠。

回想一下，自我注意本身没有任何循环或卷积，但这就是使它如此快速运行的原因。 为了使其对位置敏感，我们提供了位置编码。 这些计算如下：

为了避免在细节上占用过多空间，我们将为您提供https://github.com/Atcold/pytorch-Deep-Learning/blob/master/15-transformer.ipynb的完整代码。

具有N个堆叠的编码器层以及位置嵌入的整个编码器写为

class Encoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, ff_hidden_dim,
            input_vocab_size, maximum_position_encoding, p=0.1):
        self.embedding = Embeddings(d_model, input_vocab_size,
                                    maximum_position_encoding, p)
        self.enc_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.enc_layers.append(EncoderLayer(d_model, num_heads,
                                                ff_hidden_dim, p))
    def forward(self, x):
        x = self.embedding(x) # Transform to (batch_size, input_seq_length, d_model)
        for i in range(self.num_layers):
            x = self.enc_layers[i](x)
        return x  # (batch_size, input_seq_len, d_model)

示例

仅编码器可用于许多任务。 在随附的笔记本中，我们看到了如何将编码器用于情感分析。

使用imdb评论数据集，我们可以从编码器输出一系列文本的潜在表示形式，并通过二进制交叉熵训练该编码过程，该编码与正片或负片评论相对应。

同样，我们省去了螺母和螺栓，将您引向笔记本电脑，但这是Transformer中使用的最重要的建筑组件：

class TransformerClassifier(nn.Module):
    def forward(self, x):
        x = Encoder()(x)
        x = nn.Linear(d_model, num_answers)(x)
        return torch.max(x, dim=1)

model = TransformerClassifier(num_layers=1, d_model=32, num_heads=2,
                         conv_hidden_dim=128, input_vocab_size=50002, num_answers=2)

该模型以典型方式进行训练的地方。