自然语言处理中的深度学习

综述

• 近年来令人瞩目的成就:
  • 对于某些语言, 机器翻译比起人工翻译更受青睐
  • 在一些问答数据集上, 机器超过人类水平
  • 语言模型可以生成流利的段落 (比如, Radford et al. 2019)
• 用机器学习可以得到非常通用的模型, 从而对于每个不同的任务, 机器学习只需要少量与这个任务相关的知识

语言模型

• 语言模型给一段文字指定概率: $p(x_0,…x_n)$
• 一个句子可能由太多种词汇组合而成, 所以我们无法简单地训练一个分类器
• 这里最流行的方法是利用链式法则去分解概率分布:

神经语言模型

简单来讲, 我们把一段文字输入一个神经网络, 这个神经网络会首先把这些上下文信息映射到一个向量上. 这个向量表示了下一个词的信息. 我们有一个巨大的词嵌入矩阵, 这个矩阵里的向量对应了这个模型所有可能输出的词. 接着, 我们通过计算之前那个上下文向量与这个词嵌入矩阵里所有向量的点积, 得到预测下一个词的概率. 我们通过优化极大似然的方法训练这个模型. 通常, 我们不直接进行词级别的预测, 而是对子词(sub-word)或者字母进行预测.

图.1: 神经语言模型

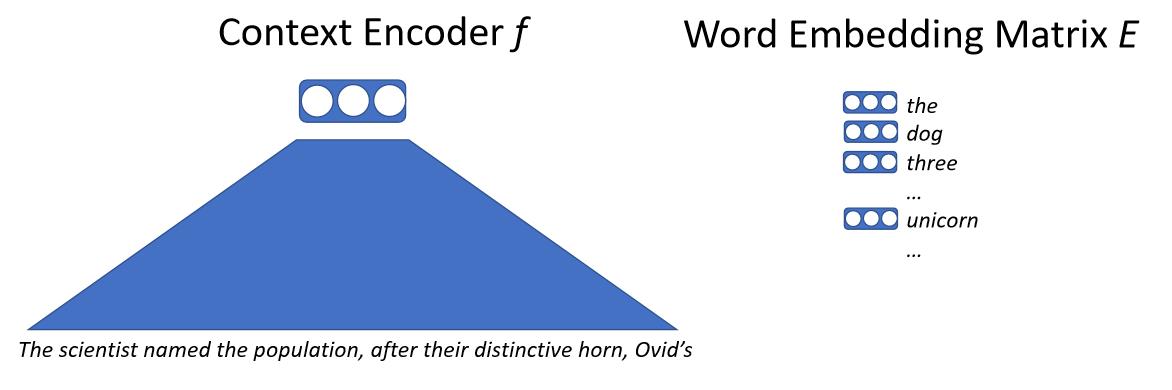
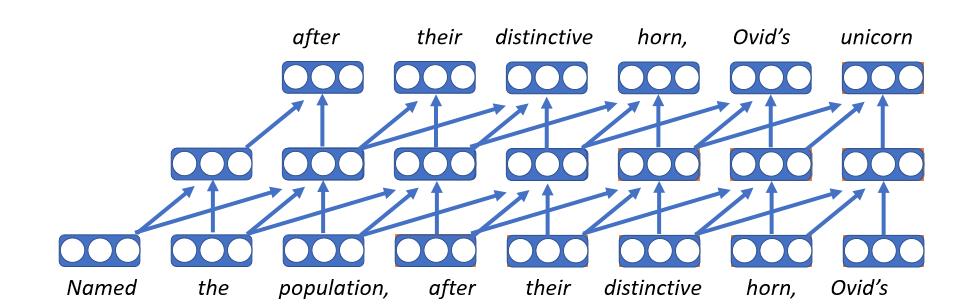
卷积语言模型

• 这是最初的神经语言模型
• 把每个词嵌入成一个向量, 它对应了词嵌入矩阵的一个条目; 因此, 无论这个词处在什么样的上下文当中, 得到的都是同样的向量表示
• 在时间维(通常在处理序列输入的时候, 比如一句话由不同词的序列组成, 我们把不同词组成的这个维度称为时间维)的每一步, 我们用同一个前向网络进行计算
• 不足的是, 卷积语言模型只能处理固定长度的历史信息, 因此, 它只考虑有限的上下文信息
• 卷积语言模型的训练速度非常快

图.2: 卷积语言模型

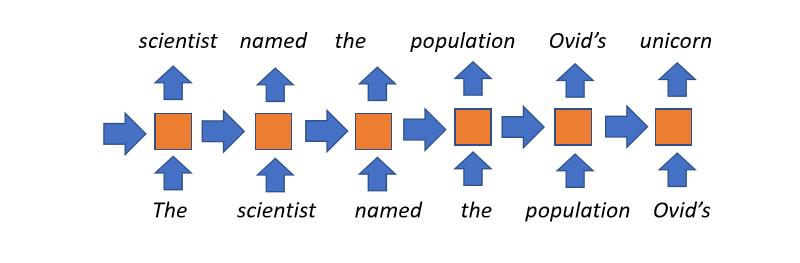
循环语言模型

• 直到近一两年前, 循环语言模型一直是最流行的方法.
• 概念上非常容易理解: 时间轴上每一步, 我们维护一个状态 (这个状态是从上一步传递过来的, 里面包含着我们之前读过的所有信息). 我们把在当前步新读到的信息融合到这个状态里, 再把它传递到下一步. 我们重复这个过程, 直到读完每一个词.
• 循环语言模型没有上下文长度的限制: 举个极端的例子, 利用循环语言模型, 一本书的标题甚至可以影响到这本书最后一个词的状态.
• 缺点:
  • 正在阅读的整个文档的历史信息都被压缩到一个固定大小的向量里了, 这个向量是循环语言模型的瓶颈
  • 当上下文信息很长的时候, 这个模型存在梯度消失(gradient vanishing)的问题
  • 因为之后步的状态计算依赖于之前步的状态, 所以无法并行化运算, 这个导致了训练速度相对较慢

图.3: 循环语言模型

Transformer语言模型

• 自然语言处理领域最新的模型
• Revolutionized penalty (eric: not sure what does this mean)
• 三个主要步骤
  • 输入
  • $n$ 层transformer (编码层), 每层的参数不共享
  • 输出
• Transformer论文中一个6层transformer编码器的示例::

图.4:Transformer语言模型

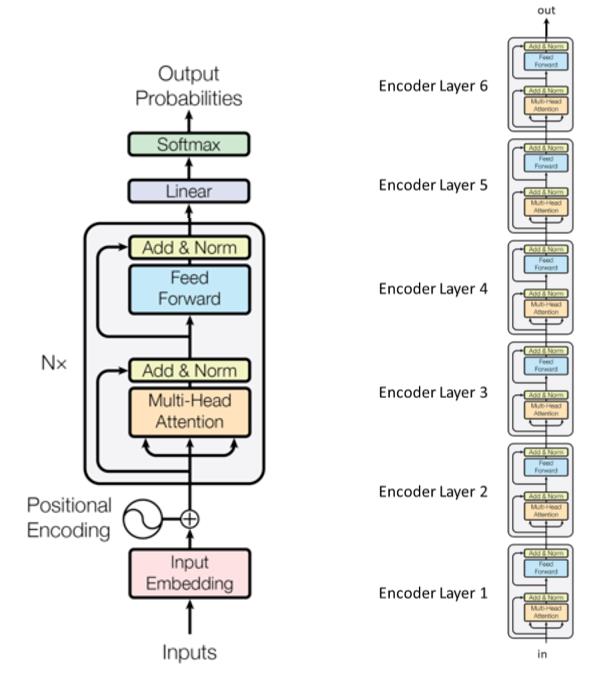
我们用”Add&Norm”来连接不同的子层(在transformer里, 我们通常用层来表示transformer模块堆叠的数量, 每个模块里存在一些子层). “Add”表示一个残差连接(详见He et al.的Deep Residual Learning for Image Recognition). 这些残差连接可以减轻梯度消失的影响. “Norm”代表层标准化(Layer Normalization).

图.5: 编码层

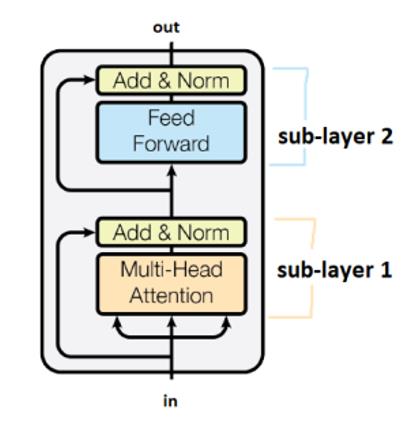
注意, 对于时间轴上的不同步, transformer公用同一套参数.

多头注意力机制

图.6: 多头注意力机制

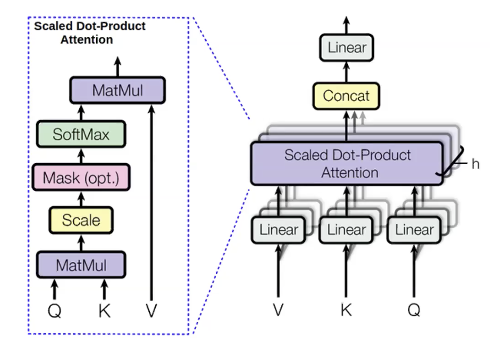
对于我们想要预测的词, 我们计算一个叫做query(q)的值. 对于这个词值钱的所有词(我们用它们来预测这个词), 我们称他们为keys(k). Query里记录了上下文信息,比如之前的形容词. Key更像是一个标签, 它当中包含了当前词的信息, 比如它是否是一个形容词. 一旦计算了$q$, 我们可以用它去计算出之前词的分布 ($p_i$):

对于之前的词, 我们同时计算一个叫做values(v)的值, 它表示了这些词的内容信息.

计算这些数值之后, 我们计算$v$的加权和, 权重是注意力机制得到的概率分布, 用这些加权和作为我们输出的隐状态(hidden states):

\(h_i = \Sigma_{i}{p_i v_i}\)

在同一时间, 我们并行运算好几组query, value和key, 这样我们就可以借助多种信息去预测下一个词. 举个例子, 当我们用”这些”, “长角的”, “银白色的”去预测”独角兽(复数, unicorns)”. 通过”长角的”和”银白色的”, 我们已经可以猜到独角兽了. 但是, 通过”这些”, 我们可以知道我们要的是一个名词的复数形态. 从而, 用全部这三个词去预测, 我们可以得到更好的结果. 多头注意力机制就是一种让模型从之前的词中考虑多种因素的方法.

相比于其他方法(比如循环神经网络), 多头注意力机制的一个重要的优势在于它很强的并行性. 它可以在同时对所有时间点的所有头进行计算. 这种运算方法随之引入一个问题: 因为它可以同时计算所有时间点, 模型是可以看到当前预测的词之后的词的 (作弊了), 我们只想要模型考虑之前的词. 一个解决方案是引入自注意力掩码(self-attention masking). 这个掩码是一个上三角矩阵, 矩阵对角线左下方的系数全部为0, 矩阵对角线右上方的系数全部为负无穷. (译者注: 这个掩码是应用在对数上的, 如果对这个矩阵求指数, 它就变成一个下三角矩阵, 左下为1, 右上为0.) 将这个掩码使用在注意力机制的输出上, 可以让模型在预测一个词的时候, 只关注它之前的词. 这个掩码很重要, 因为它让这个语言模型在数学上是正确的. 在实际操作中, 我们经常用双向的上下文信息. (注: 在双向的transformer语言模型里, 我们有两个transformer, 前向的transformer如同以上所述. 后向的transformer在实际操作中, 我们将文字序列倒序, 然后用另一个transformer去对这个倒序的的文字序列进行计算. 对于倒序的tranformer, 自注意力掩码也是必要的. 对于每一个transformer, 我们都要保证它不能”偷看”到当前预测的词之后的内容.)

在transformer语言模型里, 我们通常会给模型额外提供一种嵌入, 表示每个词的位置信息. 在语言中, 有一些信息, 比如词序, 对于模型来说非常重要. 在这里我们的方法是, 用一个额外的嵌入去学习每个词的位置信息, 然后用它们作为transformer的额外输入, 去区分同样的词在不同位置出现的情况. 这时, transformer的输入就是用来表达词信息的向量与用来表达位置信息的向量的和(注: 或者把这两个向量连接起来).

图.7: Transformer结构

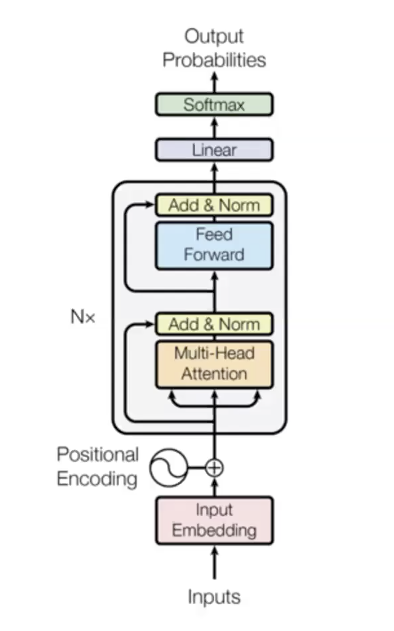
为啥这模型这么棒:

1. 它提供词与词之间的直接连接, 计算每个词的时候都可以访问到之前所有词的隐状态, 这样有效减少了梯度消失. 通过这个方法, 我们可以非常简单地学到很复杂的函数.
2. 并行运算所有时间点.
3. 自注意力机制是平方时间复杂度的 (每个词可以访问到其他所有词)

一些使用技巧 (适用于多头注意力机制和位置信息嵌入) 以及如何从语言模型中解码

技巧1: 利用层标准化来稳定训练

• 对于基于transformer的模型来说非常重要 <!–

Trick 2: Warmup + Inverse-square root training schedule

• Make use of learning rate schedule: in order to make the transformers work well, you have to make your learning rate decay linearly from zero to thounsandth steps. –>

技巧2: 学习率预热(Warmup)和逆方差学习率调整

• 合理调整学习率: 通常我们让学习率在前一千步内线性地下降.

技巧3: 谨慎初始化参数

• 对于类似机器翻译的任务, 这点很重要.

技巧4: 标签平滑化

• 对于类似机器翻译的任务, 这点同样很重要.

以下是我们之前讨论的方法的结果. 在右面列出的”ppl”代表困惑度(perplexity, 交叉熵的指数形式). ppl越低越好.

图.8: 模型性能对比

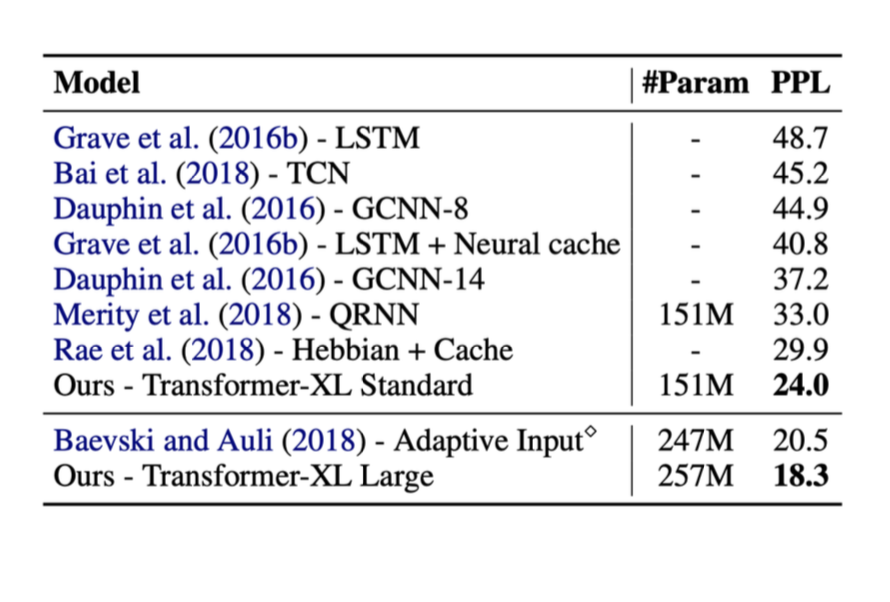
从图中可以看到, 当使用了transformer时, 模型性能有明显提升.

关于transformer语言模型的重要知识点

• 比较少的归纳偏置(Inductive Bias).
• 所有词之间都直接连接, 一定程度上解决梯度消失问题.
• 可以并行运算所有时间点. <!–

Self attention is quadratic (all time-steps can attend to all others), limiting max sequence length.

• As self attention is quadratic, its expense grows linearly in practice, which could cause a problem. –>

自注意力机制是平方时间复杂度的(任意词可以访问到其他所有词), 我们需要限制输入序列的最大长度.

• 因为自注意力机制是平方时间复杂度的, 计算开销随着序列长度线性增长, 这个会导致一些问题.

图.9: 对比Transformers和RNNs

Transformer有很好的扩展性

1.无限的训练数据, 甚至超过你需要的规模 2.GPT2 (2019年一个基于transformer的模型) 包含20亿个可训练参数 3.最近(2020年), 一些模型甚至包含170亿个参数. <!–

Decoding Language Models

We can now train a probability distribution over text - now essentially we could get exponentially many possible outputs, so we can’t compute the max. Whatever choice you make for your first word could affect all the other decisions. Thus, given that, the greedy decoding was introduced as follows. –>

从语言模型中解码

我们现在可以训练一个模型, 训练它学习一个文字上的概率分布. 因为存在指数级数量的可能输出, 我们无法轻易得到概率最高的那一个. 我们对于前面词的选择, 会影响之后所有的决策. 所以, 我们利用贪婪解码(greedy decoding)的方法.

贪婪解码可能不灵

在每一步, 我们取概率最高的那个词. 但是, 这种做法无法保证最后得到整体概率最高的序列, 因为只要在某一步取了某个词, 之后都再无机会回溯到这一步重新选取了.

穷举搜索亦不现实

如果想要穷举所有可能的序列, 需要$O(V^T)$的时间复杂度, 费时费力.

以上内容的理解问答

1. 相对于单头注意力机制(single-headed attention), 多头的好处都有啥?

   • 为了更好地预测下一个词, 模型需要观测和考虑多个因素. <!–

2. How do transformers solve the informational bottlenecks of CNNs and RNNs?

   • Attention models allow for direct connection between all words allowing for each word to be conditioned on all previous words, effectively removing this bottleneck. –>

3. Transformers是如何解决CNN或者RNN模型的信息瓶颈问题的?

   • 注意力机制允许每个词直接访问到它之前的所有词, 这种机制去除了信息瓶颈的问题.

4. 在GPU并行运算上, transformer如何区别于RNN的?

   • Transformer模型的多头注意力机制使得它可以被高度并行化, 这个在RNN中是无法做到的. 实际上, transformer用一次前向反馈就可以完成对所有时间点的计算..