不確定性下的預測和策略學習(PPUU)

簡介和問題設置

让我们去以一个完全没有强化学习的方式来学习。想想吧，我们训练很多模型，都是以一个不停犯错同时又由错误中学习的强化学习方式来学习。但这不是最好的方法，因为出错得太厉害就会送我们到天堂或地狱，到了这两个地方就没有意义去学习了。

所以，让我们说一些更「人类」的方式来学习驾驶一辆车。以转线来说说吧。比如有辆车时速100公里每小时，就是差不多一秒走30米吧，所以如果我们看30 米前方，就等於观察1秒未來的事。

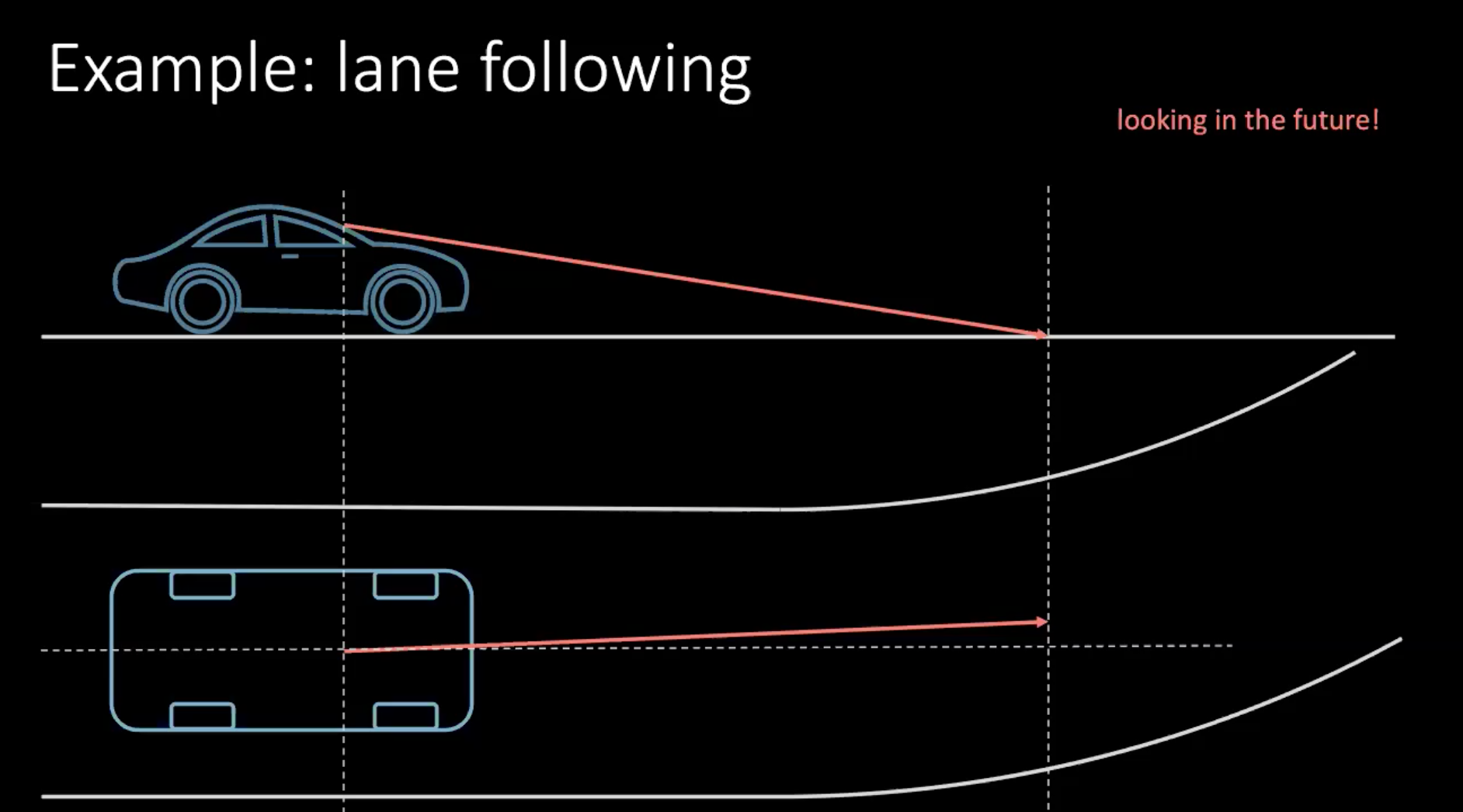
图 1: 驾驶的同时也观察未来

如果我们转向车子，那我们就要以未来会发生什么来作出决定。为了在数秒后做一个转向，我们要现在就要去作出行动，也就是要现在去转动方向盘，现在我们就正在转方向盘了。驾驶时下决定，不单单是基于你如何驾驶，也要看交通中的周围的车辆。因为周围的每一个人都不是那么确定性的，所以是十分困难来去用所有车的可能性来考虑。

现在就让我们来一步一步来解说如何运作。我们有一个代理人(以一个大脑来代表)，它以$s_t$来作为自身的输入(包括位置和速度﹑图片内容)﹑输入后就生成行为$a_t$ (转向控制，加速和煞车)。环境会送我们到下一个新状态，然后就传回一个代价值$c_t$。

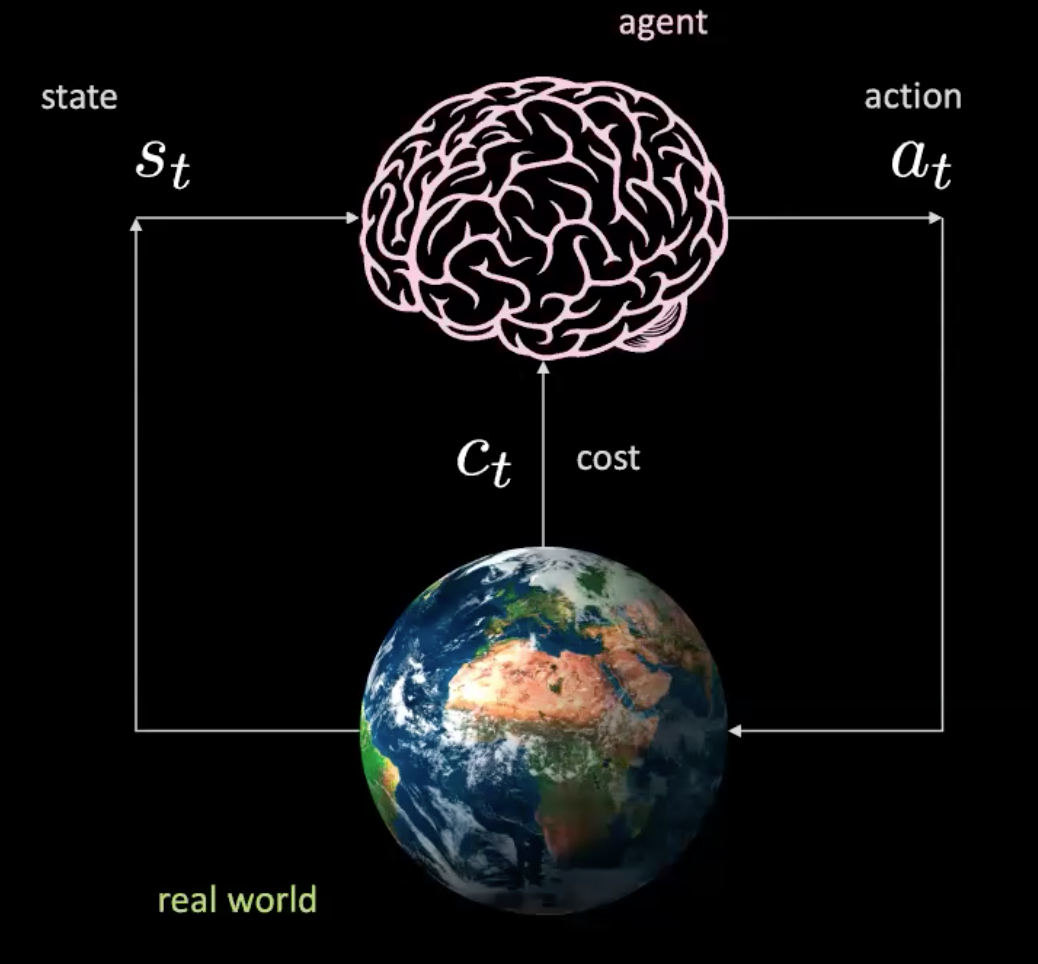
图 2: 现实世界中代理人的图示

这就如一个简单的网路，就如以下一样，当在一个特定的状态下，你作出一个行动，然后世界就给我们下一个状态和基效行动带来的后果。这是没有包括模型的，因为每一个行为都是与现实世界互动的行为。但我们可以在没有与现实世界互动下来训练一个代理人吗?

对!我们可以!就让我们在「学习世界模型」部份中找出来吧。

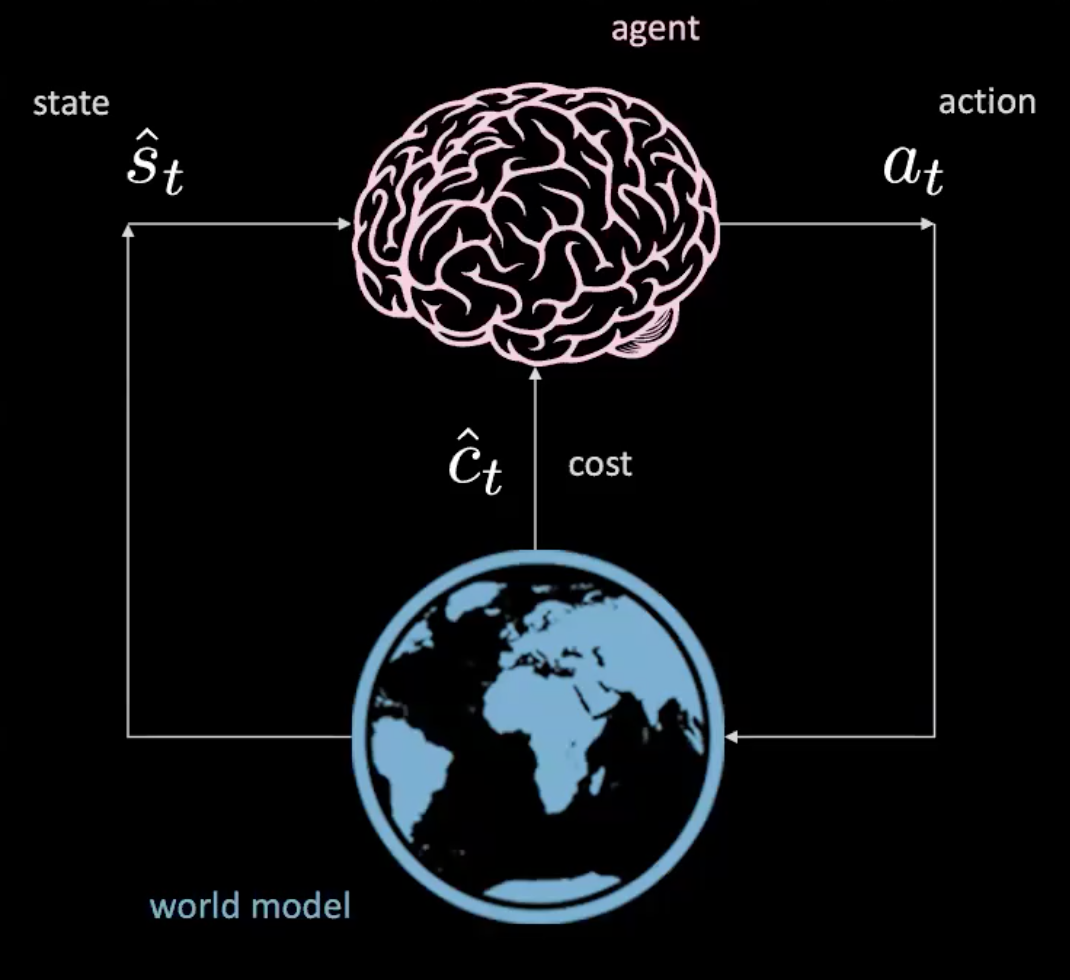
图 3: 世界模型中的代理人的图示

数据集

在说一下如何去学这个世界模型前，让我们去探索下我们所有的数据集。我们有7个摄影机安装在30层高的大厦，全都面对着州际公路。我们调整着州际公路。我们调整摄像机来影到由上方看下去的视觉，而且我们去边框每一部车和取出这些边框。在时间点$t$，我们可以确定$p_t$代表位置; $v_t$代表速度;最后$i_t$代表目前车辆周围的交通状况。

因为我们知道驾驶时的运动学的，我们可以倒过来知道司机正在做什么行动。比如，一辆车是以直线匀速来移动，我们就知道加速度是零(意思就是没有行动)

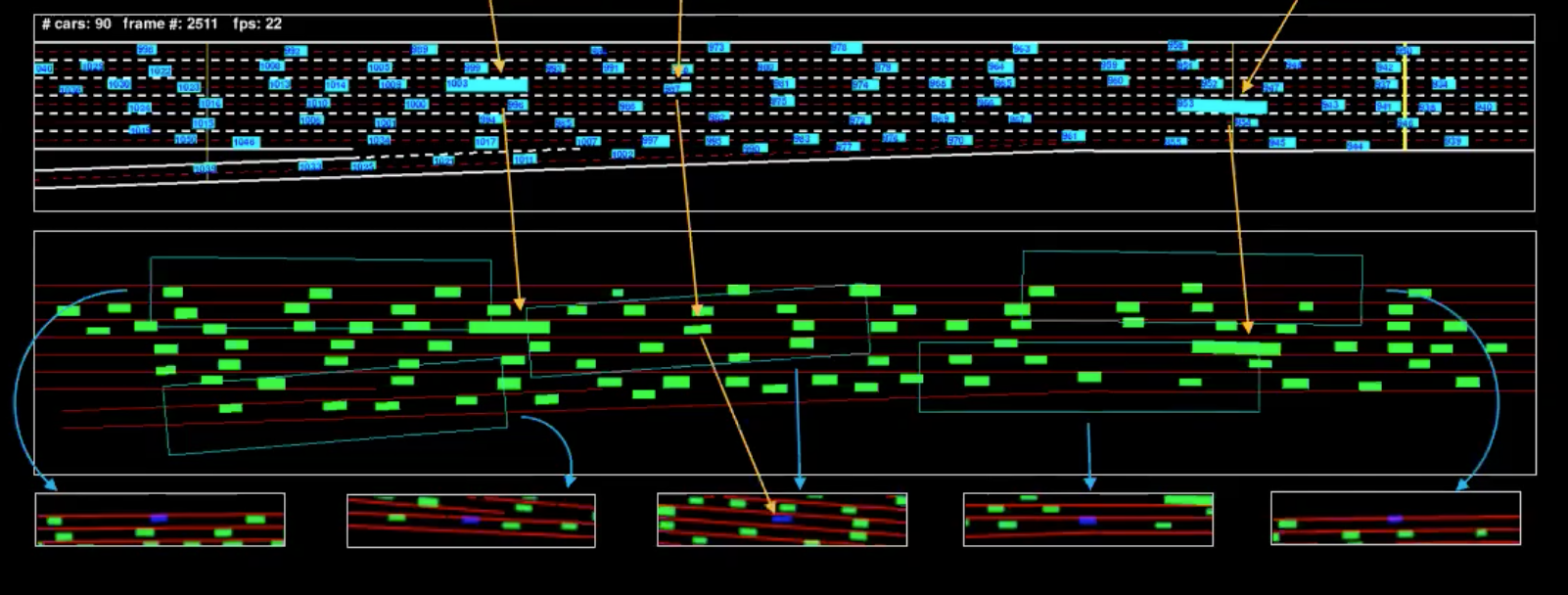
图 4: 「机器表示」表示出来的一个帧

图中蓝色的就是输入，而图中绿色的就是我们所称的「机器表示」。为了明白这点更深，我们已经从很多车辆中分出了一些车辆(图中小的长方边框们）。下方的视图们中的的边框，就是所有车辆分出来看到的部份。

代价

这里有两种不同的代价:车道代价和接近代价。车道代价说我们在一条车道中保持得有多好，然后接近代价代价说给我们有多接近别的车。

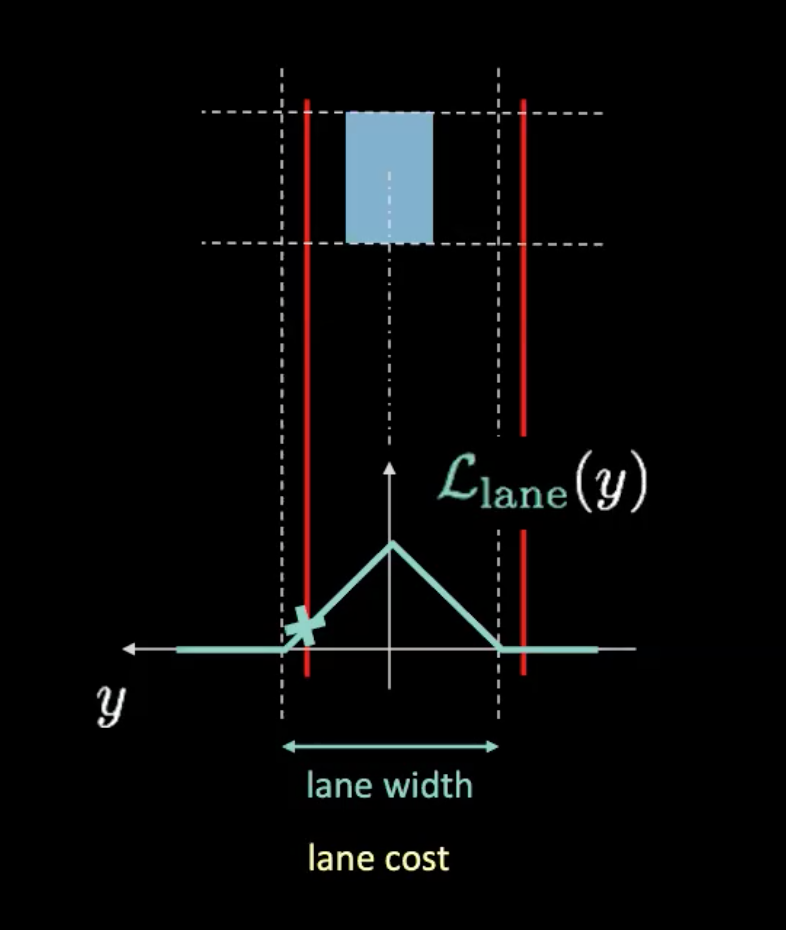
图 5: 车道代价

在上方的图，虚线代表实际的行车线，红线帮我们以现在车辆的位置来知道车道代价。红线随着我们的车的移动来移动。可能曲线（青色）和红线的交叉点的高给予我们代价值。如果车子在行车线们中间，两条红线与实际行车线们重叠的话，就会给我们零代价。相反地，当车由中间移开，红线也会移开，结果就是非零值的代价。

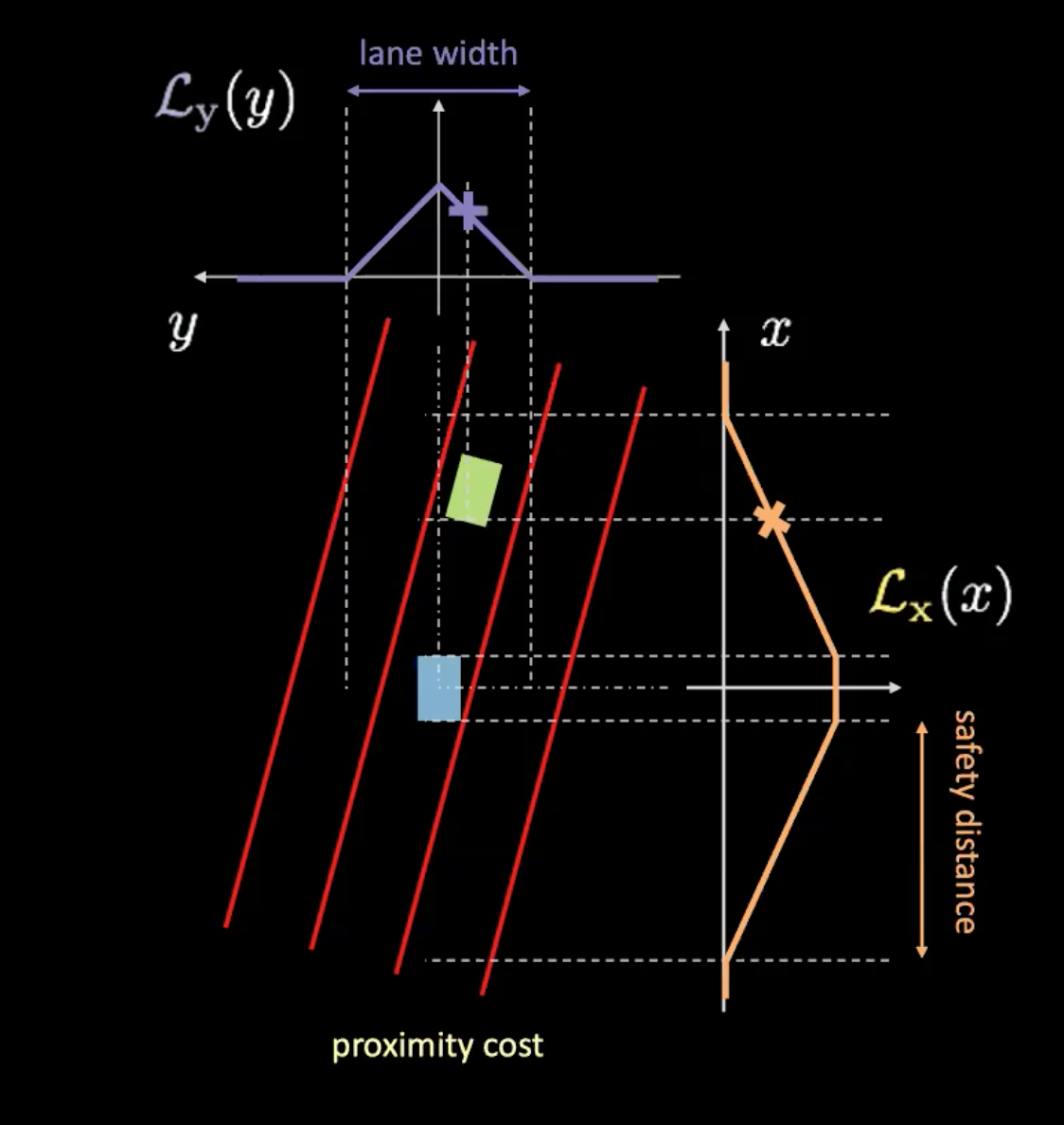
图 6: 接近代价

接近代价有两个分量($\mathcal{L}_x$和$\mathcal{L}_y$)。$\mathcal{L}_y$是和车道代价相似，而$\mathcal{L}_x$就根据于我们的车的速度。图6的橙色曲线告诉我们安全距离。当车速上升时，橙色曲线阔度扩大。所以当车行走得更快，你就要看更前方和更后方的距离。而车和橙色曲线的交叉点的高决定$\mathcal{L}_x$.。

而这两个分量的乘积给予我们接近代价。

学习世界模型

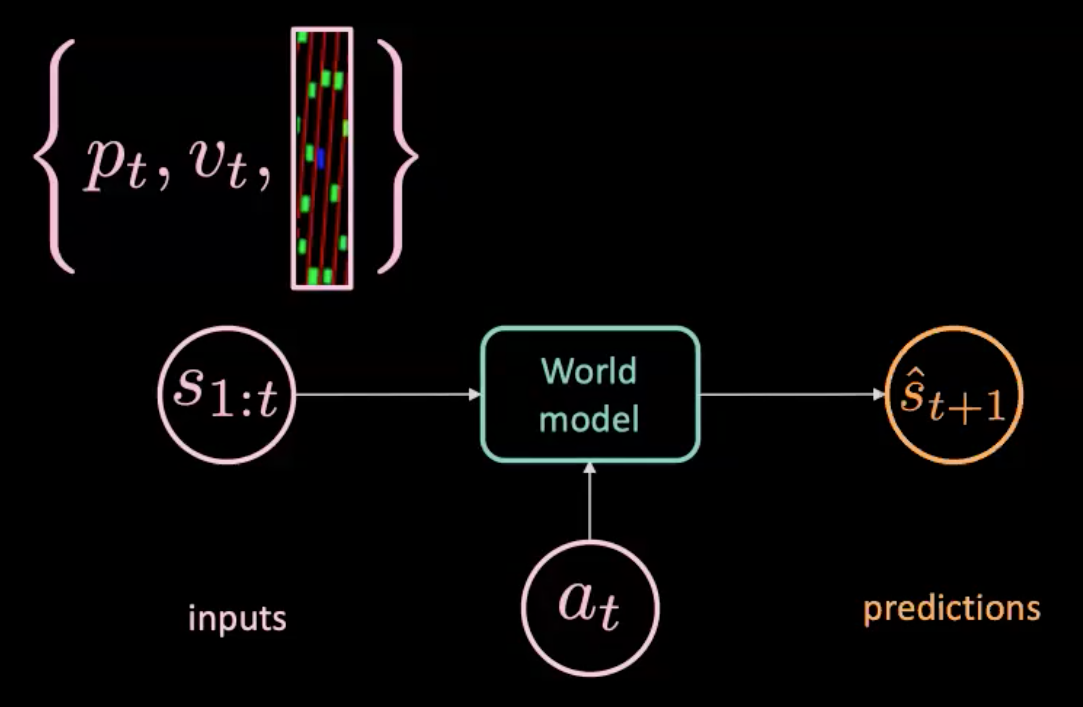
图 7: 世界模型的插图

世界模型是以行动$a_t$来作为输入(转向，刹车和加速)，而且s1:t，它是一个状态序列，每一个状态都是以位置和速度﹑状态当时的图片内容来表示，世界模型预测出下一个状态$\hat s_{t+1}$。另一方面，我们有真实世界告诉我们实际上发生了什么($s_{t+1}$)。我们用优化预测($\hat s_{t+1}$)和目标($s_{t+1}$)之间的MSE(均方误差)来训练我们的模型。

确定性预测器加解码器

其中一个训练我们的模型的方法就是用「预测器加解码器」，请看下方说明

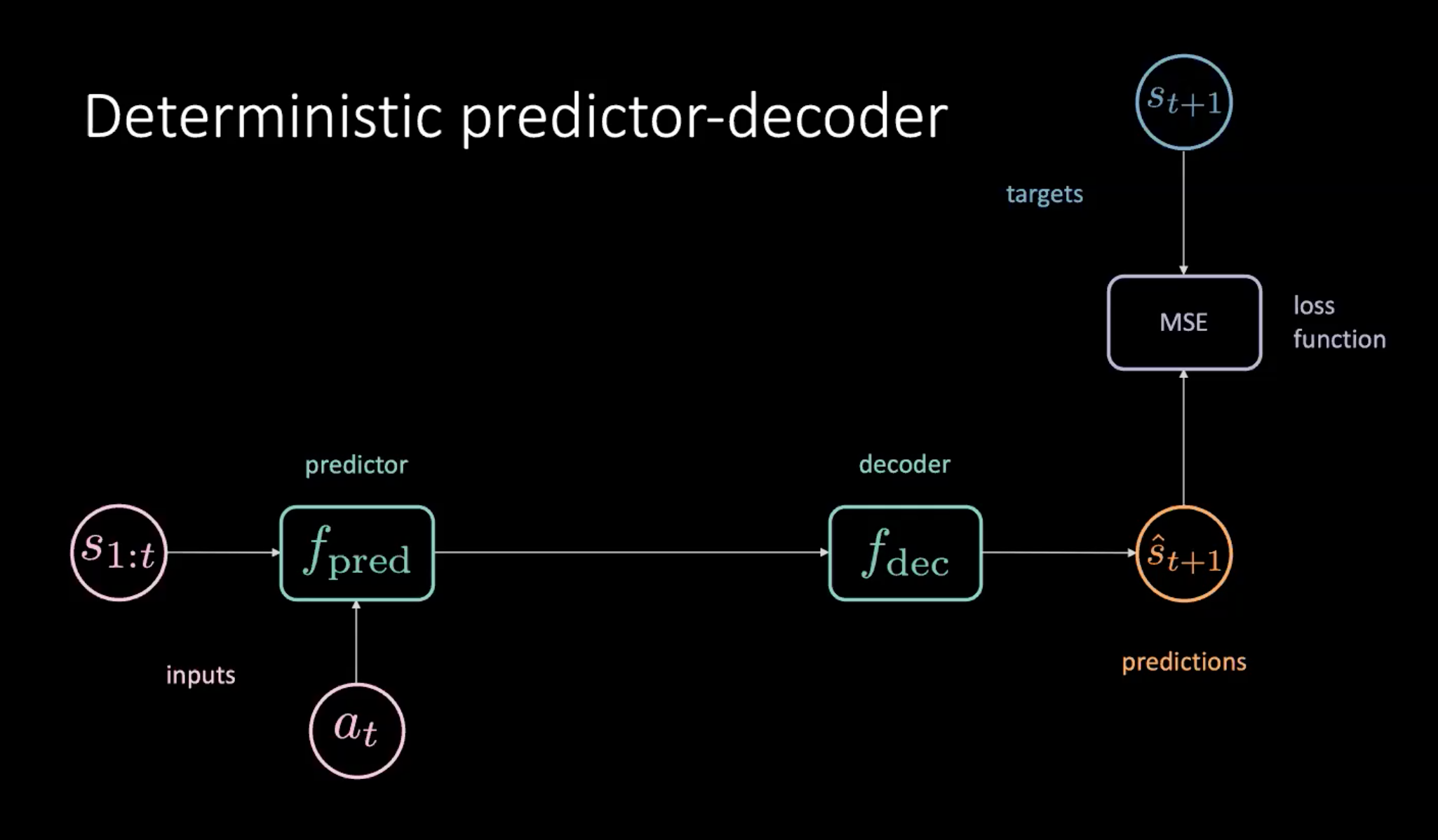
图 8: 图8：以确定性预测器加解码器来学习世界模型

就如图8所描绘的，我们有一个代表状态的序列($s_{1:t}$)和行动($a_t$)，行动就以输入来输入到预测模块。那个预测模块输出未来的隐藏表示，这个表示就传到解码器，而解码器就解码这个未来的隐藏表示和输出预测($\hat s_{t+1}$)。我们之后以最小化预测$\hat s_{t+1}$和目标 $s_{t+1}$来训练我们的模型。

图 9: 实际未来 vs. 确定性的未来

不幸地，这行不通！

我们看到确定性结果会变成很朦胧。这是因为我们的模型是平均所有可能发行在未来的可能性。这会可以几个课前讨论过的未来的多模式比较，当一枝在中心点直立的钢笔随机地向不同方向倒下。如果平均所有笔倒在地上指向的方向，那就会给我们一个认为，就是那枝笔从头到尾都没有移动过，当然就不正确了。

我们可以通过在模型中引入潜在变量来解决此问题。

变化式预测网络

为了去解决上个部份说出的问题，我们加一个低维潜在变量$z_t$到原来的网路中，然后去加多一个扩充模组$f_{exp}$来配一个合适的维度。

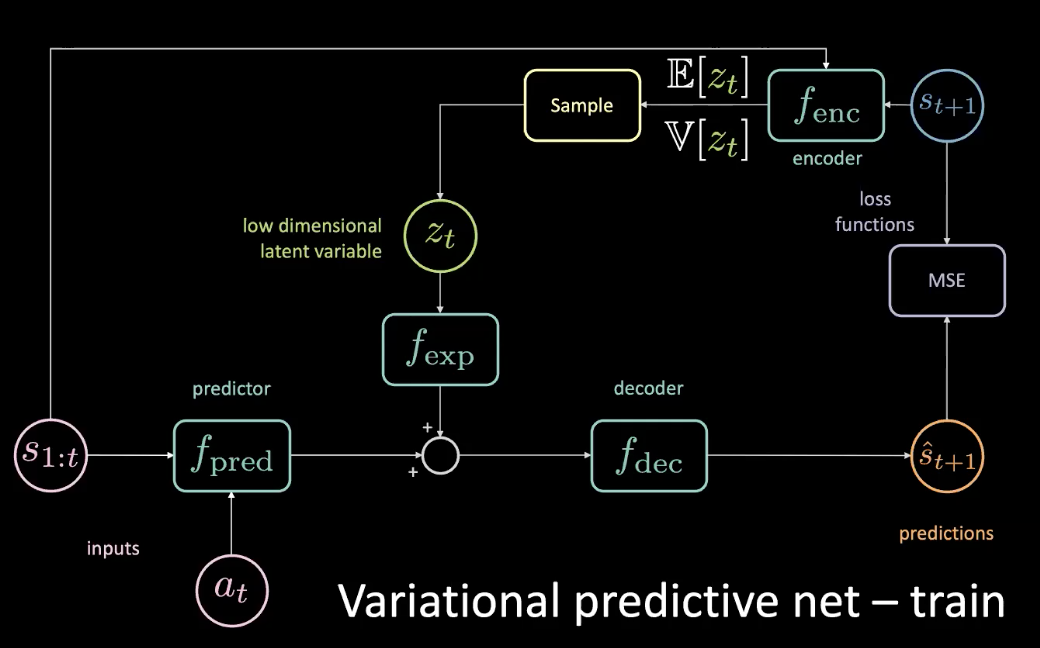
图 10: 变化式预测网络-训练

$z_t$被选来去最小化特定预测的MSE。然后去调节这个潜在变量，您仍然可以通过对潜在空间进行梯度下降来将MSE降至零。但这样做是很昂贵。所以我们可以实际预测到潜在变量使用一个解码器。解码器令用未来状态去给我们一个分布，这个分布有平均值和变异数，那我们就能用这个分布来来抽样化$z_t$。

在训练中，我们可以用这个连串方法来了解现在正在发生什么，就是去看未来会发生什么;由尽会发生什么来找取得信息;然后用这些信息来预测出潜在变量。不过的是，我们不能在测试时间中跑到未来。解决方法就是实行一个解码器去给我们一个后验分布(posterior distribution)，这个后验分布用优化KL散发(KL divergence)来尽可能地接近先验(prior )。

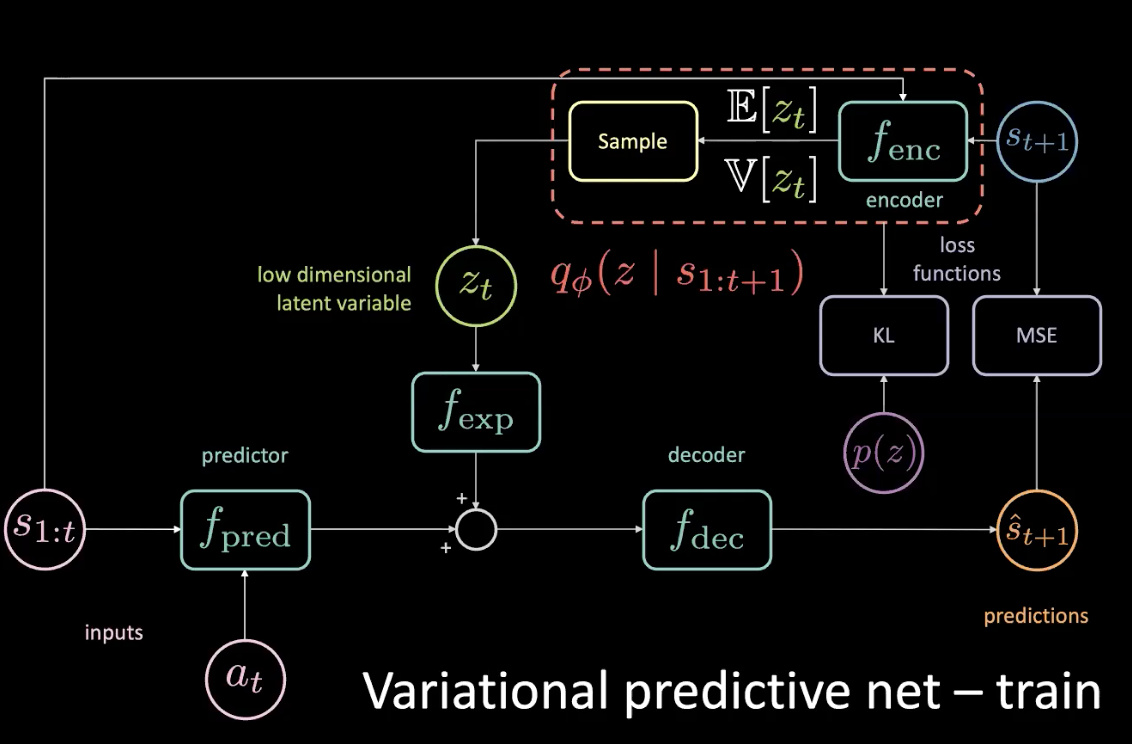
图 11: 变化式预测网路 - 训练(包括一个先验分布)

现在，让我们来看一下这个推论-我们如何驾驶?

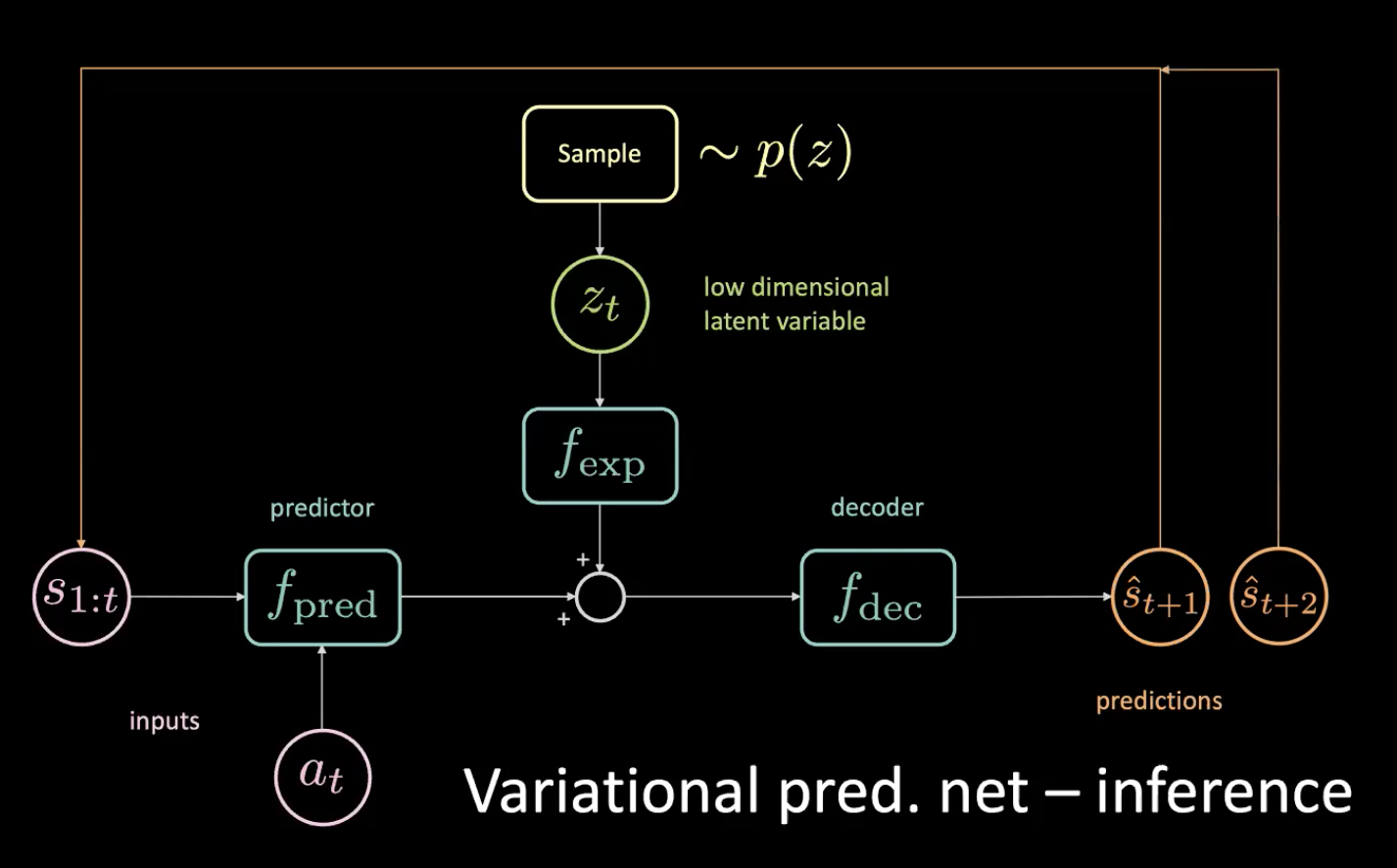
图 12: 变化式预测网络-推论

我们由先验那里抽样那个低维潜在变量$z_t$，方法是去强行令编码器去输入潜在变量z到这个分布。在得到预测$\hat s_{t+1}$后，我们就放它回去(在自动回归的步骤中)和去取得下一个预测$\hat s_{t+2}$，然后不停地这样去对网路输入。

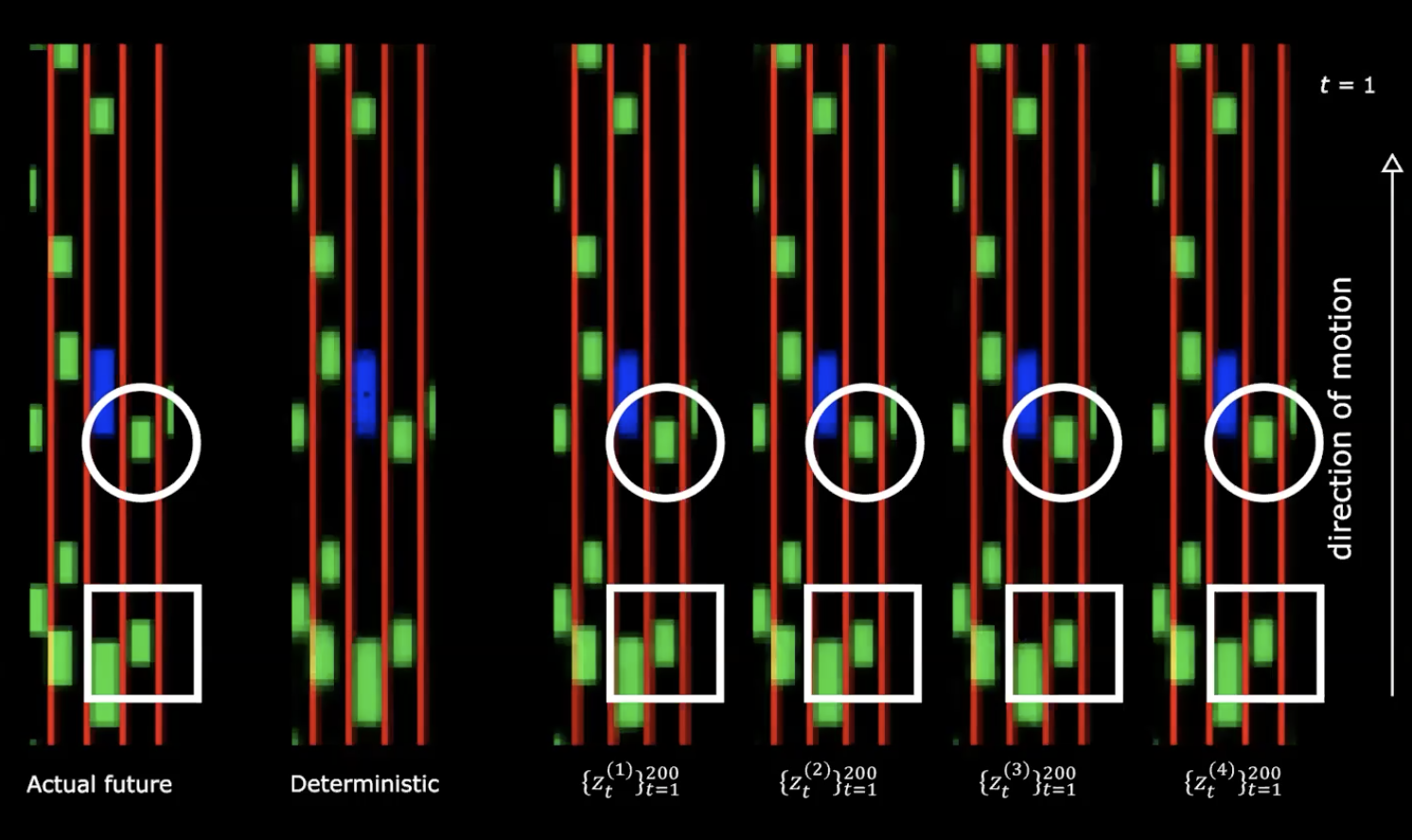
图 13: 实际未来 vs 确定性

上方的图的右边，我们可以看到来自正态分布的4个不同的绘图。我们以同样的初始状态开始，然后就提供200 个不同的值到潜在变量。

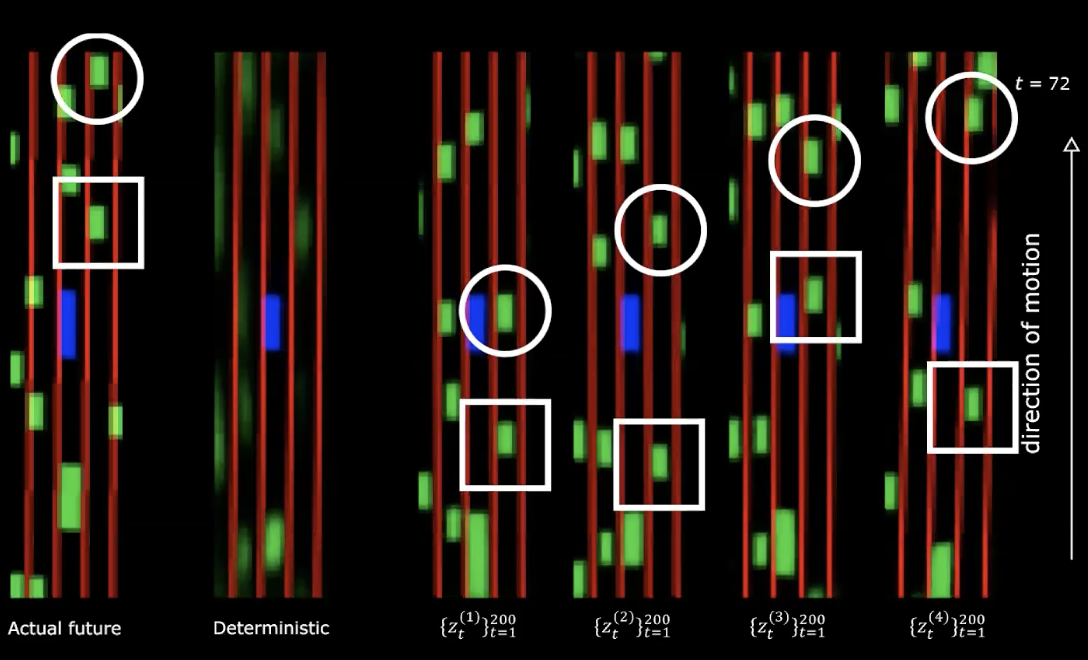
图 14: 实际未来与确定性-移动后

我们可以看到提供不同的潜在变量生成不同的状态序列，不同的状态序列有着各自不一样的行为。这意思是我们有一个生成未来会发生的事的网路。真迷死人了！

下一步是什么?

我们现在用所有的大量数据来以上方所说的优化车道代价和接近代价的方法来训练我们的网路。

这多个未来是来自你输入到网路的潜在变量序列。如果你在…在潜在的空间…执行梯度上升的话，那你就是尝试去增加接近代价，结果当然是你有一个潜在变量序列，它其他车驶向你。

动作不敏感和随机关闭潜在(latent dropout)

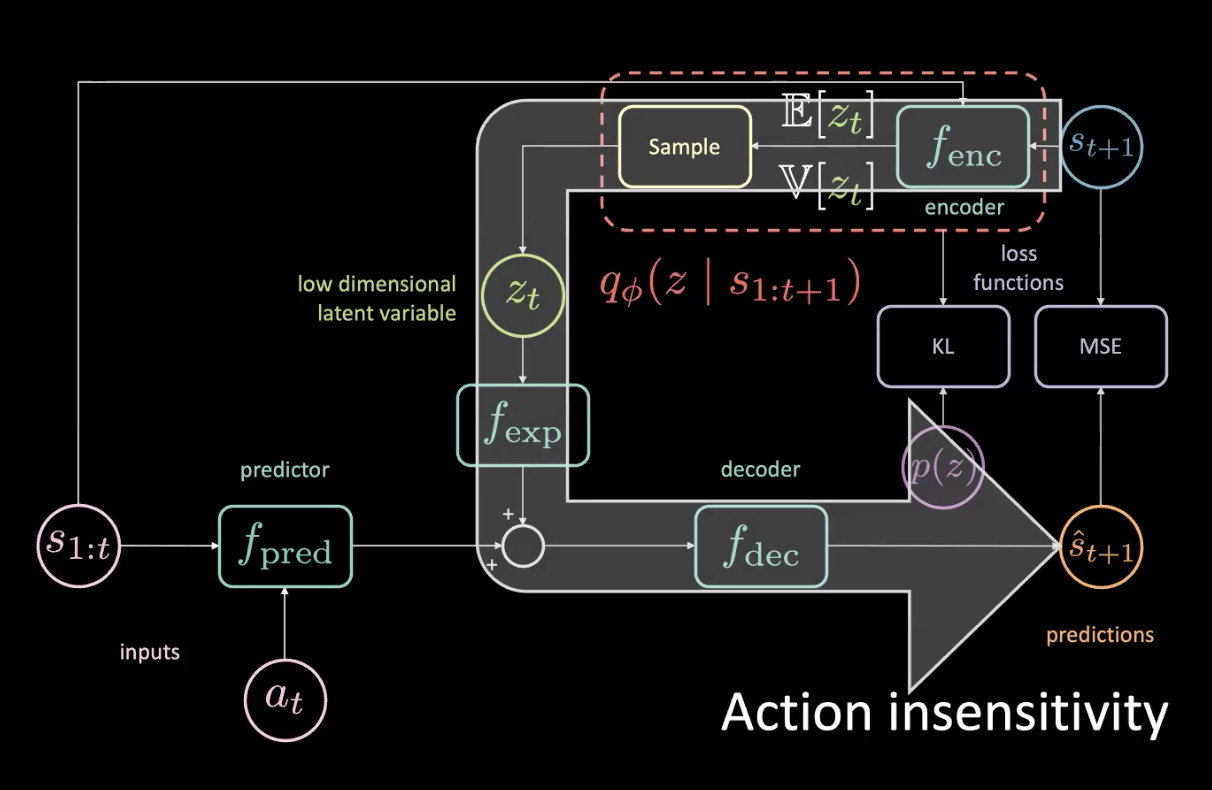
图 15: 问题-动作不敏感

比如你可以实际上可以访问未来，如果你稍微转左，所有东西就会转右，然后就令MSE大幅度下降。如果潜在变量能告诉网路下方所有东西都转右，那MSE损失就能被最小化，不过这不是我们想要的。我们能知道什么时候所有东西转向右方，那是因为这是一个确定性任务。

图15中的大箭头表示信息泄漏，因此它不对提供到预测器現在作出的现在动作有高敏感性了。

图 16: 问题-动作不敏感

在图16，最右那个图开始，它有真实潜在变量序列(能令我们取得最准确的未来潜在变量序列)和熟练者给我们的真实动作序列。而左旁边的那两个图就随机地采样一些潜在变量，但有真实动作序列，所以我们可以看到一些转向。最后一个是最左方那个，它有真实潜在变量序列，但随机地行动，所以我们看到那个转向就主要来自潜在而不是行动，也就是编码出回转和那个行动(从其他情节中采样) 。

如何才能解决这个问题?

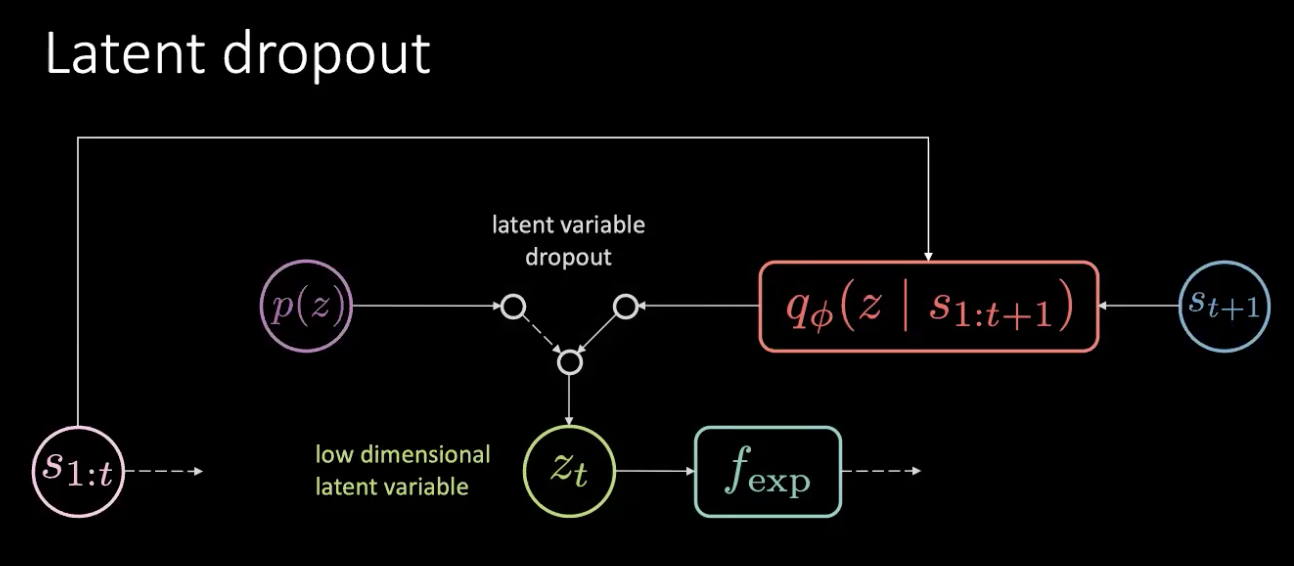
图 17: 修复 - 随机关闭潜在

这问题不是内存泄漏，而是信息泄漏。我们要对这个潜在来进行随机关闭和在先验分布随机地抽样潜在来修复这个问题。我们不会永远依赖编码器($f_{enc}$)的输出，但会由先验那里来选。这样，你就不会编码出那个在潜在变量的旋转。这样，信息就会在动作中被编码起来，而不是潜在变量。

图 18: 有着随机关闭潜在的性能

在最右边的那两个图片，我们可以看出两个不同的潜在变量们组成的集，它们有着一个真实的动作序列，和这些网路有被以随机关闭潜在的手法来训练。我们现在可以看到旋转是被行动来编码出来，而不是由潜在变量。

训练代理人

在前方的部份，我们看到如何去模拟现实世界的体验来得到一个世界模型。在这个部份，我们会用这个世界模型来训练我们的代理人。我们的目标是学习一个策略，来以之前多个状态来作出一个行动。给一个状态$s_t$ (速度和位置﹑图片内容)，代理人取一个行动$a_t$ (加速和刹车﹑转向)，那个世界模型就会输出下一个状态和代价，代价与$(s_t, a_t)$对是有关联的，也就是代价是接近代价和车道代价的组合。

就如上一个部分讨论过的,为了避免朦胧预测，我们要由未来状态$s_{t+1}$的编码器模块中或由先验分布$P(z)$中去抽样潜在变量$z_t$.世界模型得到之前的状态$s_{1:t}$和代理人作出的行动﹑潜在变量$z_t$来去预测下一个状态$\hat s_{t+1}$和代价。这个形成一个有很多重复部份模组，请看图19，它能给我们最后的预测和损失来优化。

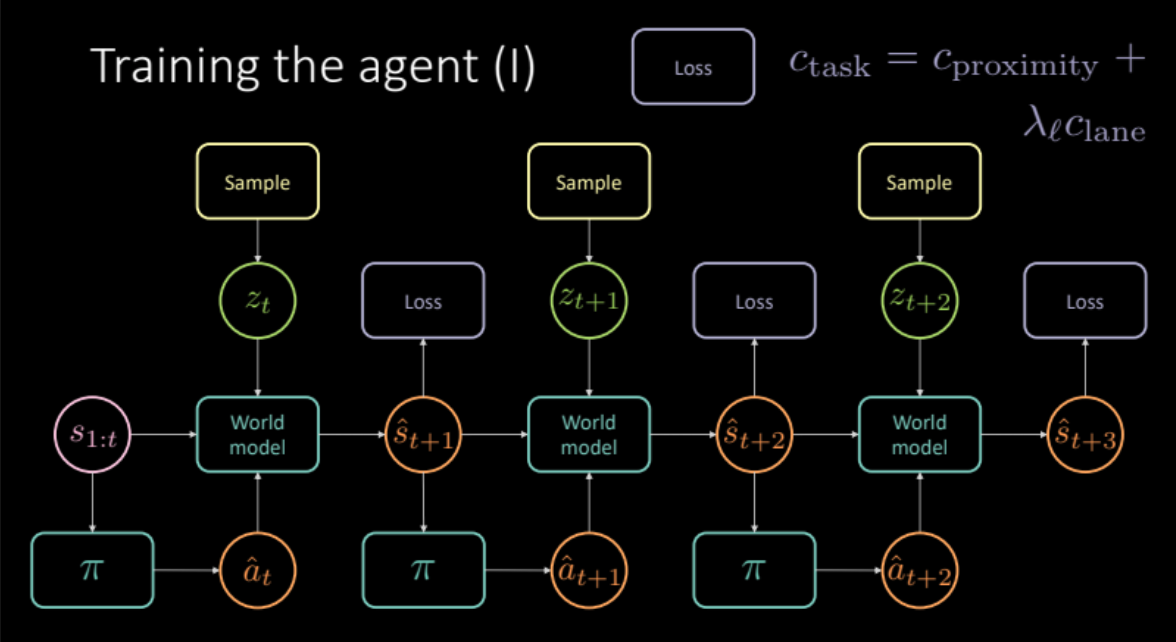
图 19: 特定任务的模型架构

所以，我们的模型预备好了。让我们看看它如何吧!!

图 20: 学习到的策略: 代理人要不就是撞了别的车，或就是移出了车道

不幸地，这不能行的。这样去训练策略是比学习去预测出全黑更没有用，因为预测出全黑带来的代价为零。

到底如何才能解决这个问题呢？我们可以模仿其他车辆来提高我们的预测吗？

对行家进行模仿

在这里，我们如何去对行家进行模仿呢?由一个尽可能接近实际未来的状态去实行一个特定的行动后，我们想要我们的模型的预测。这运作对我们的训练来说得就如一个行家式调整器expert regulariser一样。现在我们的损失函数就包括了特定任务代价(接近代价和车道代价)和这个行家式调整器。现在我们也要对应着实际未来来计算损失，那我们就必须移除模型中的潜在变量，那是因为潜在变量给我们一个特定的预测，但算了吧，如果我们只用那些平均预测的话，这个设定反而运行得更好。

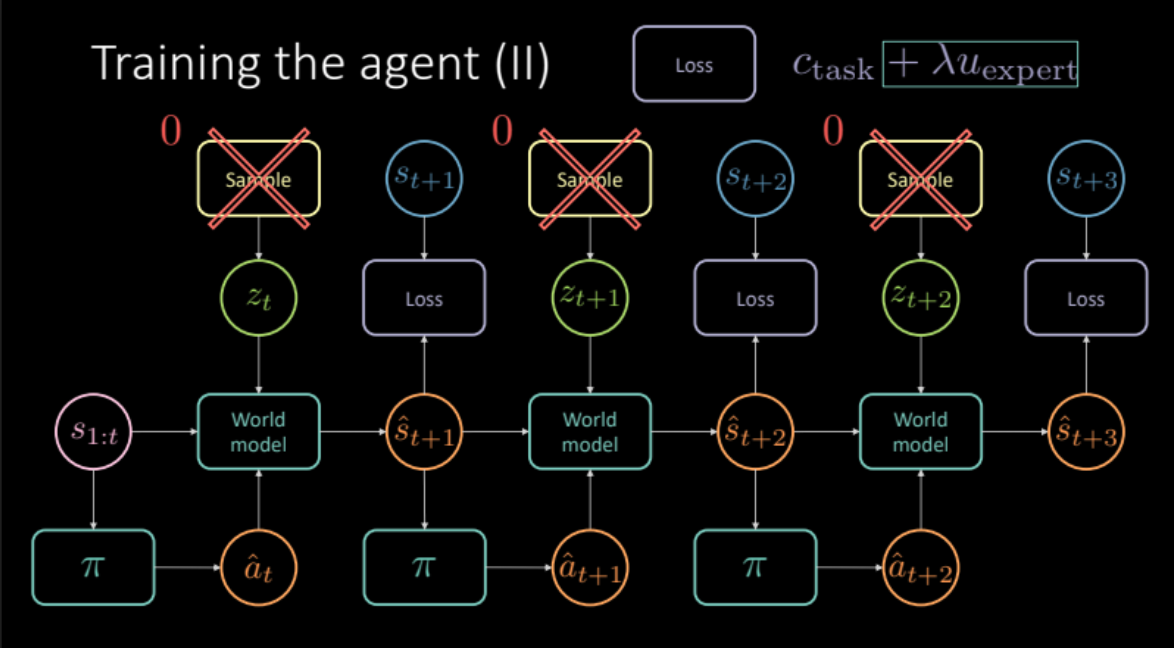
图 21: 基于模型架构的行家式调整器

所以这个模型表演得如何呢?

图 22: 由各种不同的出错到模仿行家

如我们上方能看到的图那样，这个模型表演得十分好，而且它还能学习到去做出一个好的预测。这个模型是基于模仿学习，我们尝试去模型出一个代理人去尝试模仿别人。

但我们可以做得更好吗? 我们是不是只训练出一个变化式自动编码器，但最后时却移除它?

结果就是我们当然可以做得更好，如果我们想最小化前向模型的预测所有的不确定性。

最小化前向模型的不确定性。

最小化前向模型的不确定性是什么意思和我们如何做到?在回答这个问题之前，让我们回顾一上我们在第三星期的动手做吧

如果我们用同样的数据去训练多个模型，所有的模型都会认同训练区(下方红色的那个)上的点都会带来变异数为零。但如果我们由训练区那里移开，那损失函数的轨迹就会发散和变异数的数值上升。图23就描绘出这样的事出来。但因为变异数是可微的，我们可以对变异数运行梯度下降来最小化它。

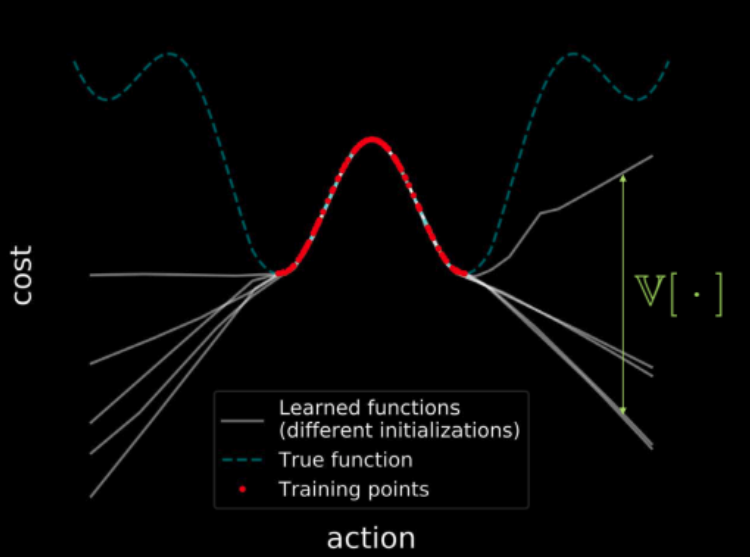
图 23: 在成个输入空间中可视化代价

回到我们的讨论，我们看到只去观察数据来学习一个策略是很难的，因为在运行时生成的状态的分布和训练时的或许不一样。世界模型或许在训练时的定义域以外的域做一些任意的预测，结果就是这任意的预测错误地带来低代价。这个策略网路或许之后就会在动力学模型中利用这些错误来生成动作，然后就引起错误的以为所有东西都行了的状态。

去解决这个，我们去外加一个代价，这个代价测量动力学模型自身的预测所有的不确定性。计算出这个的做法是这样的，把同样的输入和同样的行动输入到多个不同的随机关闭罩(dropout masks)，之后去计算不同输出的变异。这令策略网络去只生成模型认为有信心的行动。

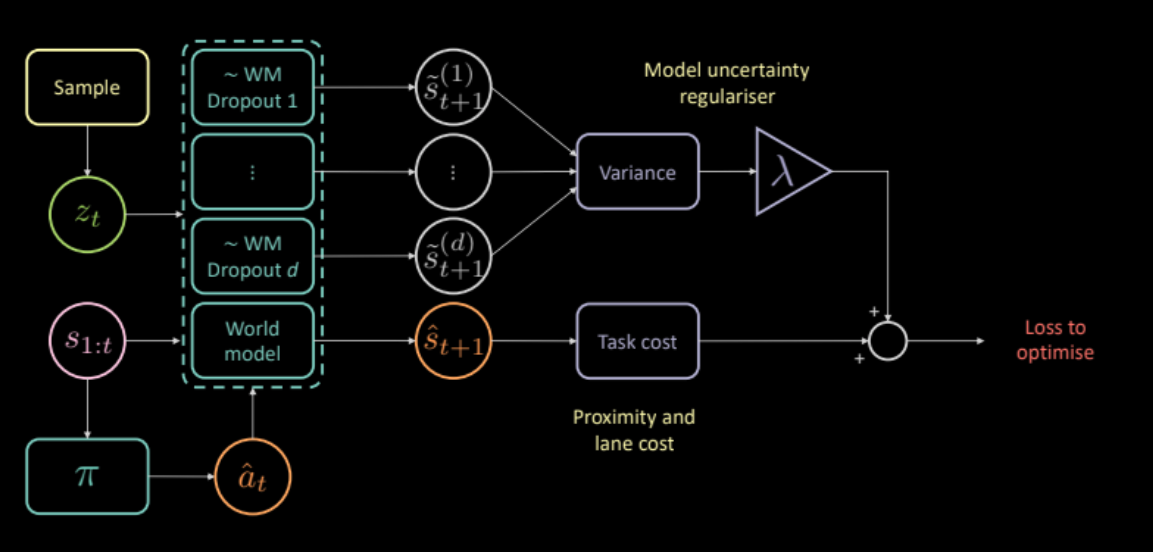
图 24: 基于模型架构的不确定度调整器

所以，这个不确定度调整器有没有去帮我们训练一个更好的策略?

对的，它有。这种学习方式的策略是比之前的模型学得更好。

图 25: 基于不确定度调整器学出来的策略

评估

图26显示出在一个交通繁忙的环境下，我们的代理人所学的驾驶的能力有多好。黄车就是原来的驾驶员，而蓝车就是我们学习了如何驾驶的代理人，而绿色车看不见我们(不能控制)。

图 26: 具有不确定度调节器的模型的性能