损失函数（连续的）以及用于基于能量的模型的损失函数

二元交叉熵(BCE)损失函数 - nn.BCELoss()

这种损失函数是交叉熵在只有两个类的情况下的简化版本。这用于测量重建误差，例如自编码器中的重建误差。此公式假定$x$和$y$是概率，因此它们严格在0和1之间。

KL散发(Kullback-Leibler Divergence)损失函数 - nn.KLDivLoss()

这是一个简单的损失函数，适用于当目标是one-hot（即$y$是一个类别）的情况。再次假设$x$和$y$是概率。它的缺点是没有与softmax或log-softmax合并，因此可能存在数值稳定性问题。

###使用Logits的BCE损失函数-nn.BCEWithLogitsLoss（）

此版本的二元交叉熵损失的输入没有通过softmax，因此不假定x在0到1之间。所以其使用sigmoid激活函数以确保结果在该范围内。这样损失函数更有可能在数值上稳定。

边际排位损失函数(Margin Ranking Loss) - nn.MarginRankingLoss()

边际排位损失是重要的损失类别。如果两个输入，此损失函数表示你想要一个输入比另一个输入至少大一定幅度。在这种情况下，$ y $是\ {-1，1 } $中的二元变量$ \。想象这两个输入是两个类别的分数。你希望正确类别的分数至少比不正确类别的分数大一定幅度。像合页损失函数一样，如果$ y *（x_1-x_2）$大于边际，则损失为0。如果小于边际，则损失线性增加。如果将其用于分类，则小批次中$ x_1 $是正确答案的分数，$ x_2 $是得分最高的错误答案的分数。如果在基于能量的模型中使用（稍后讨论），则此损失函数将降低正确答案的分数$ x_1 $并提高错误答案的分数$ x_2 $。

三重边际损失 (Triplet Margin Loss) - nn.TripletMarginLoss()

该损失函数用于测量样本之间的相对相似性。例如，让两个相同类别的图像通过CNN，获得两个向量。你希望这两个向量之间的距离尽可能小。如果让两个不同类别的图像通过CNN，则希望这些向量之间的距离尽可能大。此损失函数尝试将第一距离降为0，将第二距离提高至至少某个边际值。但是，唯一重要的是同类别图像之间的距离小于不同类图像之间的距离。

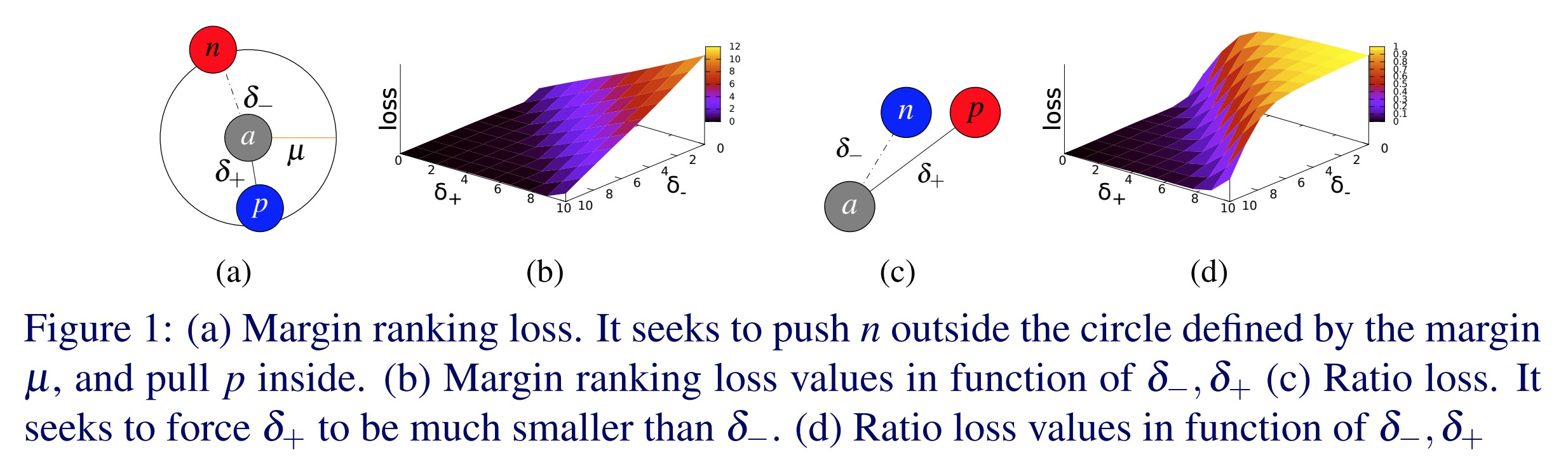
Fig. 1: Triplet Margin Loss

这一函数最初是用来训练Google的图片搜索系统的。用户在Google中键入查询请求，系统会将其编码为一个向量，然后把该向量与先前有索引的图像中对应的向量进行比较。然后，Google会检索返回距离该向量最近的图像。

软边际损失(Soft Margin Loss) - nn.SoftMarginLoss()

创建一个criterion来优化输入的张量$ x $和目标张量$ y $（包含1或-1）之间的两元分类逻辑损失。

*softmax版本的边缘损失。你有一些正负标签的数据去放入softmax。然后此损失函数尝试使正确的$ x [i] $的$ \ text {exp}（-y [i] * x [i]）$比其他任何一个都要小。 *此损失函数希望将$ y [i] * x [i] $的正值拉得更近一些，并将负值推得更远一些，但是与硬边际相反，对损失有一些连续的，指数性衰减的影响。

多类合页损失(Multi-Class Hinge Loss) - nn.MultiLabelMarginLoss()

这种基于边际的损失使不同的输入具有可变数量的目标。在这种情况下，你有几个要给出高分的类别，它会求出所有类别的合页损失的总数。对于EBM，此损失函数可将想要高分的类别的损失降低，将其他类别的损失提高。

合页嵌入损失 (Hinge Embedding Loss) - nn.HingeEmbeddingLoss()

合页嵌入损失用于半监督学习，通过测量两个输入相似或不相似，它将相似的聚集，将不相似的推开。$ y $变量指示这对分数是否需要朝某个方向发展。使用合页损失，如果$ y $为1，则分数为正；如果$ y $为-1，则分数为一个边际值$ \ Delta $。

余弦嵌入损失 (Cosine Embedding Loss) - nn.CosineEmbeddingLoss()

该损失使用余弦距离来测量两个输入是否相似或不相似，并且通常用于学习非线性嵌入或半监督学习。

• 换一种说法，1减去两个向量之间的夹角的余弦就是标准化的欧几里得距离。
• 这样做的好处是，当你有两个向量，并且想要使他们的距离尽可能大，很容易让网络使向量变长来实现。当然这不是最优解。你不希望系统将向量变大，而是将向量沿正确的方向旋转，因此你可以对向量进行归一化并计算归一化的欧几里得距离。
• 对于值为正数的情况，这种损失试图使向量尽可能对齐。对于负数对，此损失试图使余弦小于特定的边际量。这里的边际应该是一些小的正值。
• 在高维空间中，球面的赤道附近有很多区域。归一化之后，所有的点现在都在球面上被归一化了。你需要的是在语义上与你相似的样本。不相似的样本应互为正交。你不希望它们彼此相对，因为相对极只有一个点。相反，在赤道上有很大的空间，因此你希望将边际设为较小的正值，以便可以利用这一大空间的优势。

连接主义者的时序分类损失 Connectionist Temporal Classification (CTC) Loss - nn.CTCLoss()

计算连续（未分段）时间序列与目标序列之间的损失。

• CTC损失求出输入与目标可能对齐的概率的和，产生一个相对每一个输入节点可微分的损失值。
• 输入与目标的对齐方式假定为“多对一”，这限制了目标序列的长度，使其必须小于或等于输入长度。
• 当你的输出是一系列向量时非常有用，该向量对应于各个类别的分数。

Fig. 2: CTC Loss for speech recognition

应用示例：语音识别系统

• 目标：每10毫秒预测正在被发音的是哪个单词。
• 每个单词由一系列声音表示。
• 根据人的说话速度，不同的声音长度可能会映射到同一单词。
• 找出从输入序列到输出序列的最佳映射。一个好的方法是使用动态编程来找到最小成本路径。

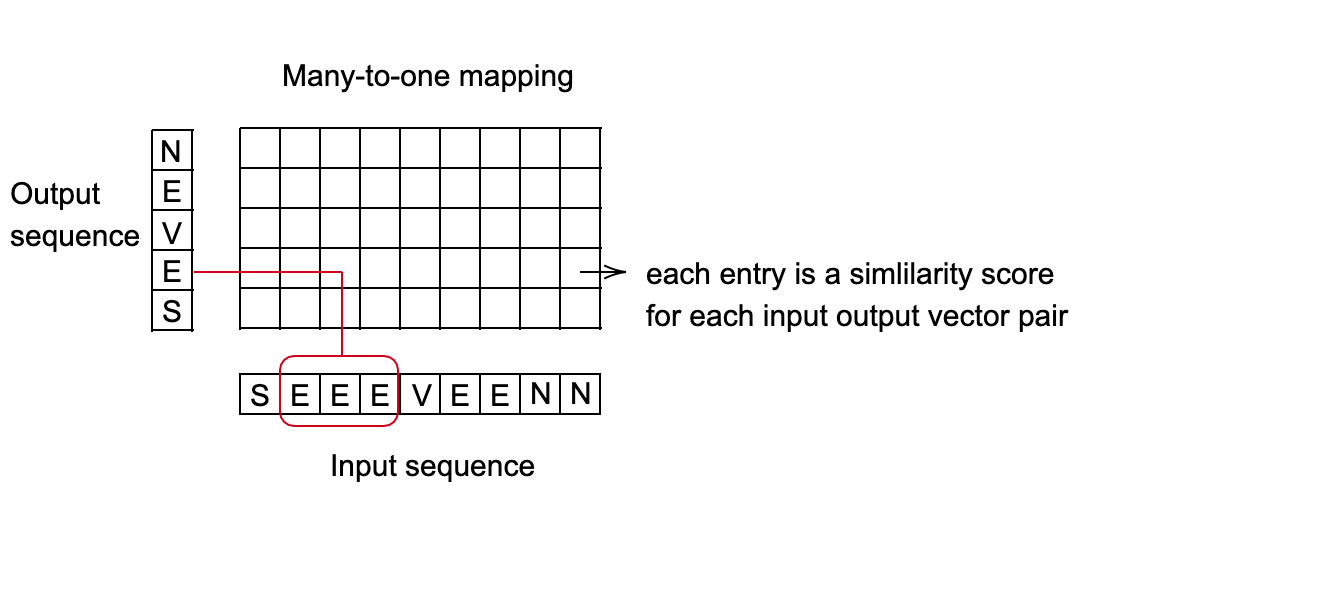
Fig. 3: 多对一映射设置

基于能量的模型（第四部分）-损失函数

架构和损失泛函数

能量函数家族： $\mathcal{E} = {E(W,Y, X) : W \in \mathcal{W}}$。

训练集： $S = {(X^i, Y^i): i = 1 \cdots P}$

损失函数：$\mathcal{L} (E, S)$ *泛函数是另一个函数的函数。在这里泛函数$\mathcal{L} (E, S)$是能量函数$E$的函数。 *因为$E$由$W$参数化，所以我们可以将泛函数变成$ W $的损失函数：$W$: $\mathcal{L} (W, S)$ *在训练集上测量能量函数的质量 *在样本的排列和重复下不变。

训练: $W^* = \min_{W\in \mathcal{W}} \mathcal{L}(W, S)$.

损失泛函数形式:

• $L(Y^i, E(W, \mathcal{Y}, X^i))$ is 是每个样本的损失
• $Y^i$ 是期望的答案，可以是类别或整个图像等。
• $E(W, \mathcal{Y}, X^i)$是给定$X_i$随着$Y$变化的能量面
• $R(W)$ 为正则化项

设计一个好的损失函数

降低正确答案的能量。

提高错误答案的能量，尤其是当它们比正确答案能量更高时。

损失函数示例

能量损失 (Energy Loss)

这个简单的损失函数会降低正确答案的能量。如果网络设计有误，你可能会得到一个大部分区域都是平坦的能量函数，因为你只在让正确答案的能量变小，而没有在任何其他地方提高能量。系统可能因此整个崩溃。

负对数似然损失 (Negative Log-Likelihood Loss)

这种损失函数会降低正确答案的能量，同时根据所有答案的概率按比例增加它们的能量。当$\beta \rightarrow \infty$时，这就是感知器损失。它已在许多社区中使用了很长时间，用于具有结构化输出的区分性训练。

一个概率模型是一种EBM，其中：

*能量可以在Y上积分（要预测的变量） *损失函数为负对数似然函数

感知器损失 (Perceptron Loss)

与60年前的感知器损失非常相似，并且始终为正，因为最小值也是从$Y^i$取的，因此：$E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$。同样的计算表明，只有在$Y^i$是正确答案的情况下，它才会完全为零。

这种损失使正确答案的能量变小，同时使所有其他答案的能量尽可能大。但是，这种损失并不能防止该函数为每个错误答案$Y^i$赋予相同的值，因此从这个意义上讲，它对于非线性系统而言并非良好的损失函数。为了改善这种损失函数，我们定义了錯誤答案中最接近正確答案的答案。

广义边际损失 (Generalized Margin Loss)

錯誤答案中最接近正確答案的答案: 离散的情况 令$Y$为离散变量。然后对于训练样本$(X^i,Y^i)$,錯誤答案中最接近正確答案的答案 $\bar Y^i$ 是所有错误答案中能量最低的答案：

錯誤答案中最接近正確答案的答案：连续的情况 令$ Y $为连续变量。然后对于训练样本$(X^i,Y^i)$，錯誤答案中最接近正確答案的答案 $ \ bar Y ^ i $是与正确答案至少$ \ epsilon $远的所有答案中能量最低的答案。

In the discrete case, the most offending incorrect answer is the one with smallest energy that isn’t the correct answer. In the continuous case, the energy for $Y$ extremely close to $Y^i$ should be close to $E(W,Y^i,X^i)$. Furthermore, the $\text{argmin}$ evaluated over $Y$ not equal to $Y^i$ would be 0. As a result, we pick a distance $\epsilon$ and decide that only $Y$’s at least $\epsilon$ from $Y_i$ should be considered the “incorrect answer”. This is why the optimization is only over $Y$’s of distance at least $\epsilon$ from $Y^i$.

If the energy function is able to ensure that the energy of the most offending incorrect answer is higher than the energy of the correct answer by some margin, then this energy function should work well.

在不连续的情况下，錯誤答案中最接近正確答案的答案是能量最小但不是正确答案的答案。在连续情况下，$Y$的能量非常接近$Y^i$，应当接近$E(W,Y^i,X^i)$。此外，在$ Y $上评估的$\text{argmin}$不等于$ Y ^ i $将为0。因此，我们选择一个距离$ \ epsilon $并决定只有距离$Y_i$至少$\epsilon$远的$Y$应该被认为是“错误答案”。这就是为什么优化仅在距离$Y_i$至少$\epsilon$远的$Y$上进行的原因。

如果能量函数能够确保“錯誤答案中最接近正確答案的答案”的能量比正确答案的能量高出一定程度，那么该能量函数应该可以良好运作。

广义边际损失示例

合页损失 (Hinge Loss)

Where $\bar Y^i$ is the most offending incorrect answer. This loss enforces that the difference between the correct answer and the most offending incorrect answer be at least $m$.

其中$\bar Y^i$是錯誤答案中最接近正確答案的答案。这种损失迫使正确答案与錯誤答案中最接近正確答案的答案之间的差异至少为$ m $。

Fig. 4: Hinge Loss

Q: 怎么选择$m$的值？

A: 可以任意选择，但它会影响网络最后一层的参数。

对数损失（Log Loss）

This can be thought of as a “soft” hinge loss. Instead of composing the difference of the correct answer and the most offending incorrect answer with a hinge, it’s now composed with a soft hinge. This loss tries to enforce an “infinite margin”, but because of the exponential decay of the slope it doesn’t happen.

这可以被认为是“软”合页损失。它用一个“软”合页而不是一般的合页来区分正确答案和錯誤答案中最接近正確答案的答案。这种损失试图施加“无限边际”，但是由于斜率的指数衰减，这种情况不会发生。

Fig. 5: Log Loss

平方-平方损失（Square-Square Loss）

该损失将能量的平方与合页的平方结合在一起。这种组合试图最大程度地减小能量，但要对錯誤答案中最接近正確答案的答案产生至少$m$的边际。这与孪生神经网络的损失非常相似。

其他的损失

还有许多其他的损失函数。这里有一个各种损失函数的总结。

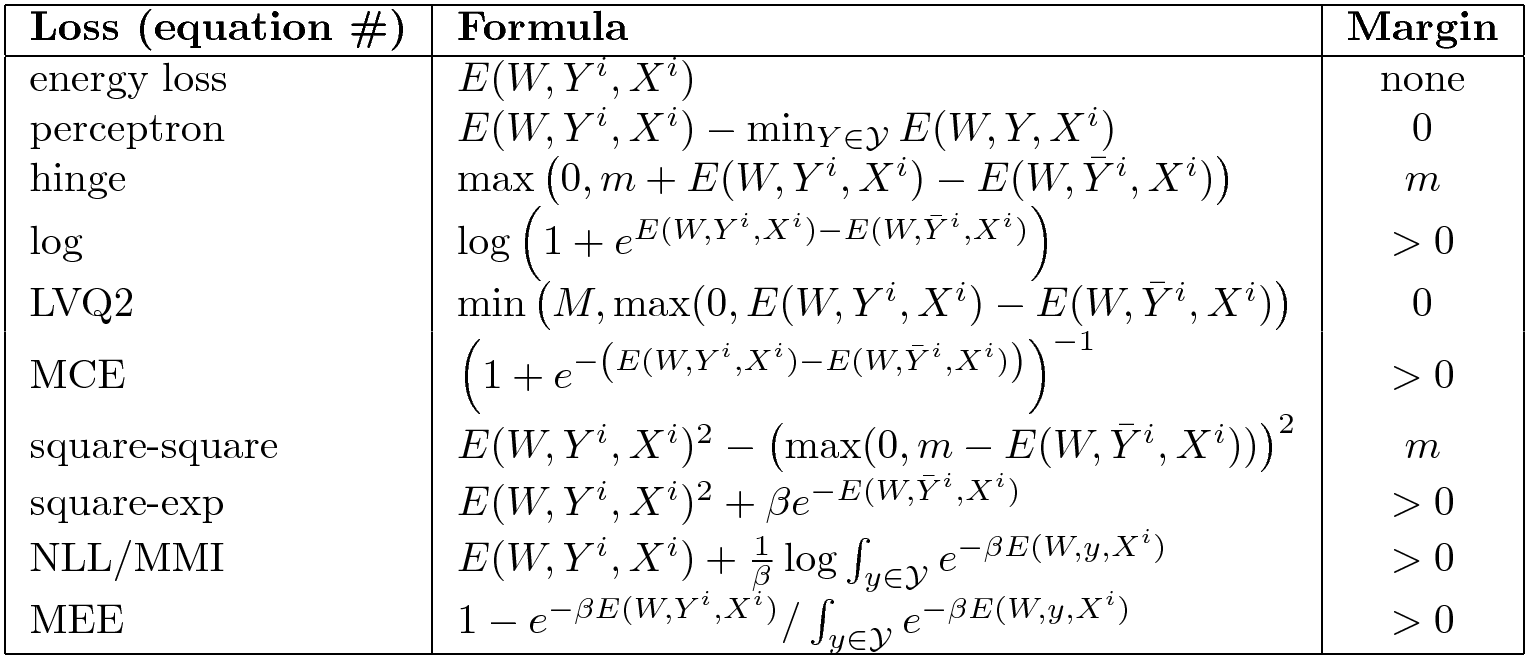
Fig. 6: EBM损失函数的选择

右边一栏显示能量函数是否要求一定的边际。最基本的能量损失不会在任何地方提高能量，因此没有边际。能量损失并并适用于所有问题。一般而言，感知器损失可以用于当你将能量线性参数化的时候，但是不是任何情况都适用。它们中有些有一个有限的边际，比如合页损失，有些有无限边际，比如软合页损失。

Q: 在连续的情况下，錯誤答案中最接近正確答案的答案 $\bar Y_i$ 是如何找到的？

A: 你想要在距离$Y^i$足够远的地方提高能量，因为如果它们太近了，参数可能不会改变太多，因为一个由神经网络定义的函数是“僵硬”的。但是一般来说，这是个困难的问题，那些选择对比样本的方法就是试图解决这个问题。并没有一个单一的正确的方法。

一个对比损失的更广泛的形式是：

我们假设$Y$是离散的，但是如果它是连续的，那么求和就会变成求积分。这里$E(W, Y^i,X^i)-E(W,y,X^i)$是$E$在正确答案和一些其他答案上面所得到的值的差值。$C(Y^i,y)$是边际，并且通常是一个$Y^i$和$y$之间的一个距离的量度。这样的理由是我们想在错误样本$y$上面提高的程度应该取决于$y$和正确样本$Y_i$之间的距离。这可能是一个更难优化的损失函数。