激活功函数和损失函数(第一部)
🎙️ Yann LeCun激活功函数
今天的讲课,我们想回顾一些重要的激活函数和它们如何在Pytorch中实现。们来自各种论文,声称这些函数可以更好地解决特定问题。
线性整流函数(ReLU) - nn.ReLU()
\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]
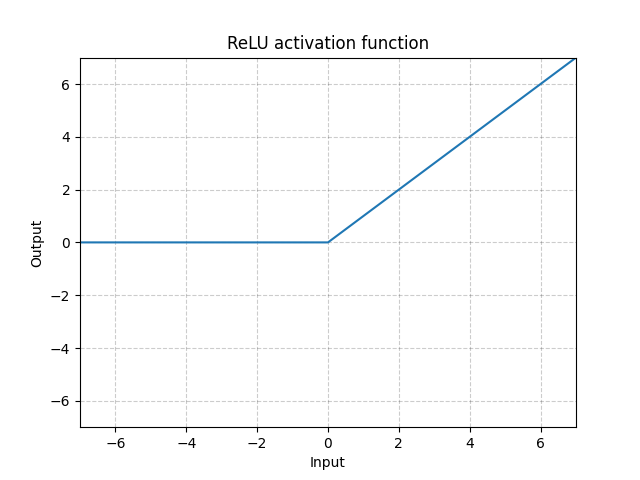
图 1: 线性整流函数(ReLU)
随机纠正线性单元(RReLU) - nn.RReLU()
很多ReLU的变化版。随机Relu(RReLU)定义如下。
\[\text{RReLU}(x) = \begin{cases} x, & \text{if} x \geq 0\\ ax, & \text{otherwise} \end{cases}\]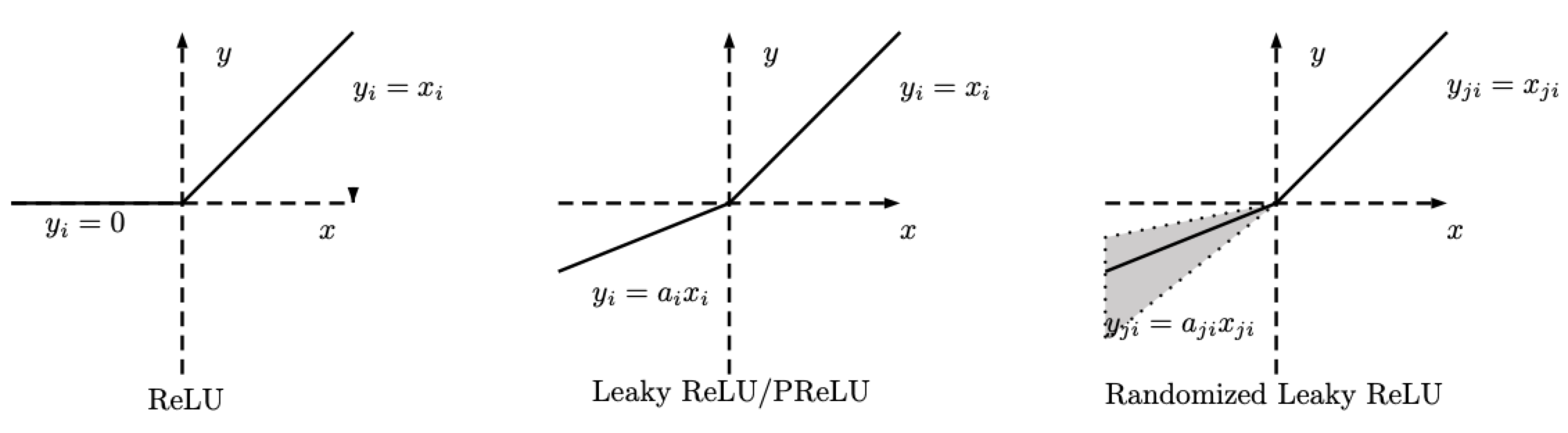
图 2: ReLU, 泄漏形ReLU /PReLU, RReLU
注意一下RReLU, $a$ 是一个随机变量,它令抽取样本的行为在一个训练时给予的全距中,而在测试时是保持不变。这个 PReLU , $a$ 是学习出来的。而泄漏形 ReLU, $a$ 是不变的。
泄漏形 ReLU(LeakyReLU) - nn.LeakyReLU()
\[\text{LeakyReLU}(x) = \begin{cases}
x, & \text{if} x \geq 0\\
a_\text{negative slope}x, & \text{otherwise}
\end{cases}\]
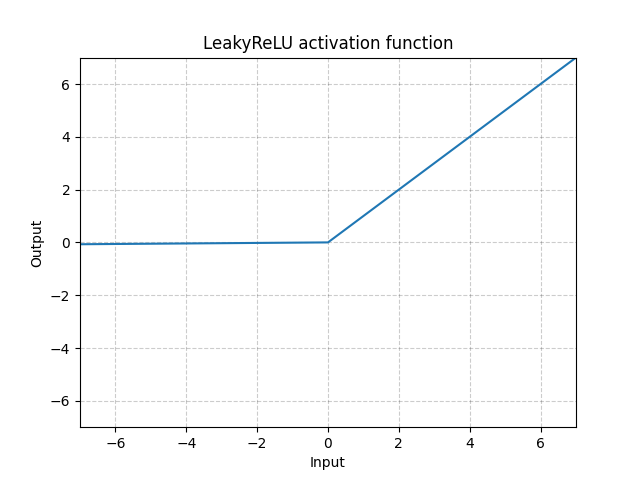
图 3: 泄漏形 ReLU
这个$a$是一个固定的参数。方程式的第二部份防止ReLU出现如同死了一样的问题,也就参考那个问题,也就是当ReLU神经元对任何输入出现不活性和只输出0 。所以,当它的梯度是零。就用负斜率,这容许网路回流一些梯道(propagate back)和学到一些有用的。
泄漏形ReLU (Leaky ReLU)对很少层的网路来说是有必要的,基本上是没可能令基本形的ReLU来回流一些梯道。以泄漏形ReLU ,网路可以有梯度,即使是在一个都是零的地方。
PReLU - nn.PReLU()
\[\text{PReLU}(x) = \begin{cases}
x, & \text{if} x \geq 0\\
ax, & \text{otherwise}
\end{cases}\]
这$a$是一个可学习的参数。
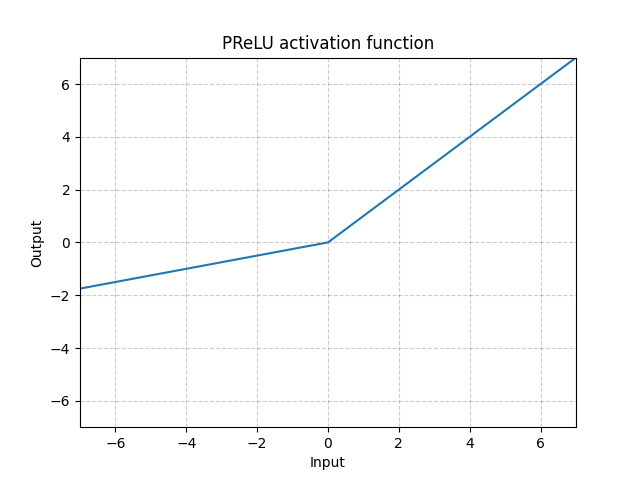
图 4: ReLU
上方的激活功能函数们(即ReLU,LeakyReLU,PReLU)都是缩放不变量。
软加(Softplus) - Softplus()
\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]
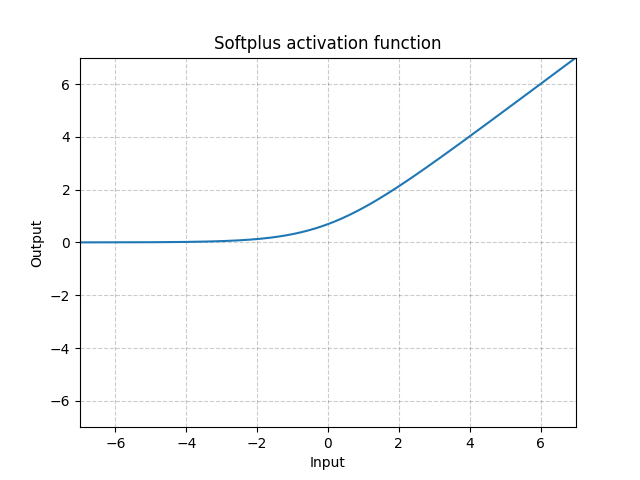
图 5: 软加(Softplus)
软加是ReLU函数中的一个平滑的近似法,它能够用来限制机器的输出为永远都是正。
如果$\beta$越来越大,该函数就变得更像ReLU。
ELU - nn.ELU()
\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1)\]
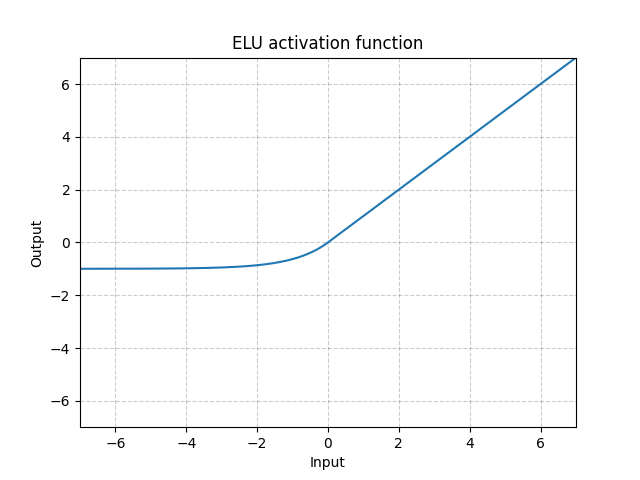
图 6: ELU
和ReLU不一样,它可以低于0,这使系统的平均输出为零。所以,这个模型或收敛得更快。而且它的变种(CELU,SELU)都只是用不同的参数化
CELU - nn.CELU()
\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1)\]
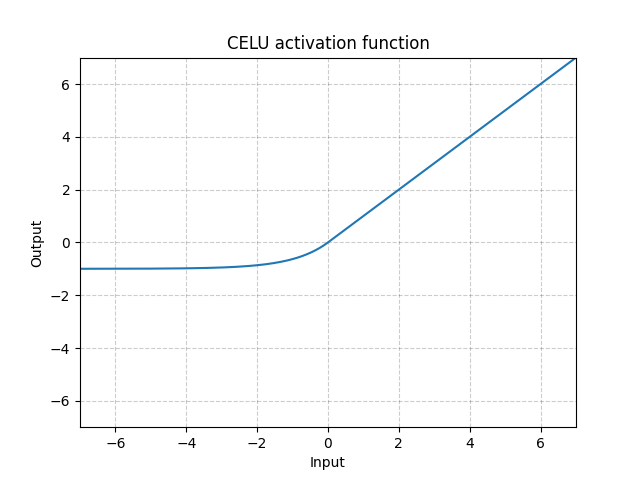
图 7: CELU
SELU - nn.SELU()
\(\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1))\) scale意思是标度
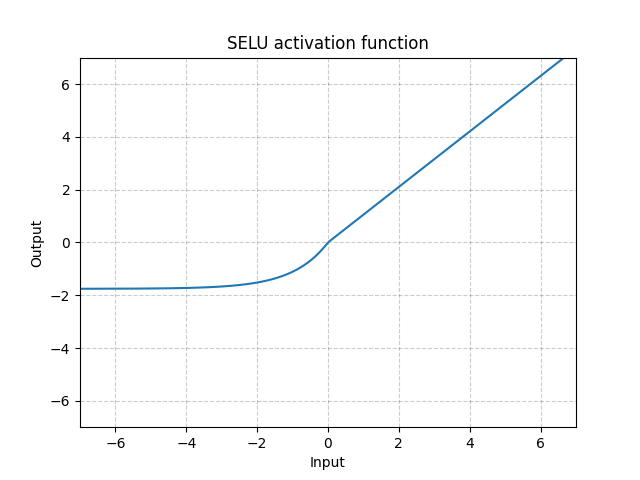
图 8: SELU
GELU - nn.GELU()
\[\text{GELU(x)} = x * \Phi(x)\]
其中 $\Phi(x)$ 是高斯分布的累积分布函数。
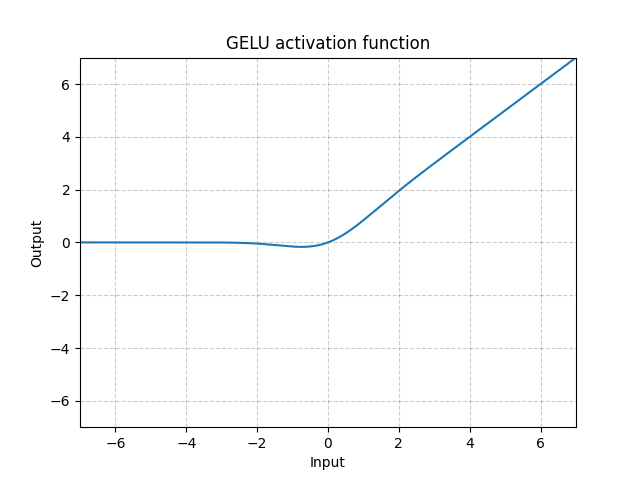
图 9: GELU
ReLU6 - nn.ReLU6()
\[\text{ReLU6}(x) = \min(\max(0,x),6)\]
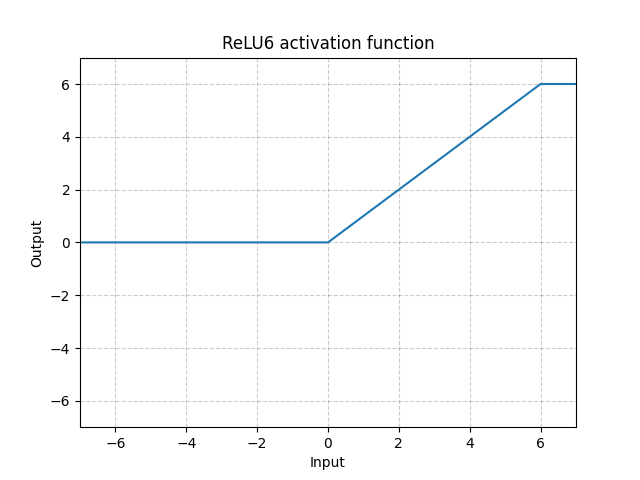
图 10: ReLU6
这个ReLU在6就已经饱和不动了。但是没有特别的原因来选6为饱和点,所以我们以用下方的S型函数 (Sigmoid function)来做得更好。
S型函数(Sigmoid) - nn.Sigmoid()
\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}\]
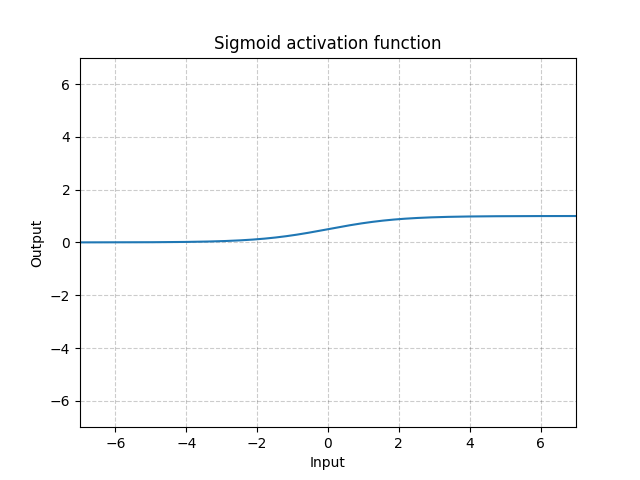
图 11: Sigmoid
如果我们在很多层中堆一些S型函数,系统学习效率可能会变低和要求好的初始化。这是因为输入是很大或很细,那S型函数的梯道就会接近零。在这个例子中,这里是没有梯道回流来更新参数,被称为饱和梯度问题。因此,对于深度神经网络,最好使用单扭结函数(例如ReLU)。
Tanh - nn.Tanh()
\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]
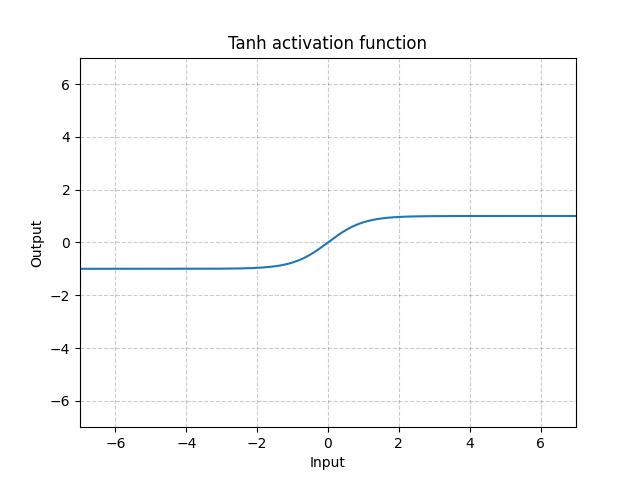
图 12: Tanh
tanh基本上就如S型函数一样,只是它是在中间的,值域为-1到1。而函数的输出的平均值基本上为0。所以,模型会收敛得更快。注意,请注意,如果每个输入变量的平均值接近零,那收敛通常会更快。一个例子就是批量标准化。
Softsign - nn.Softsign()
\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]
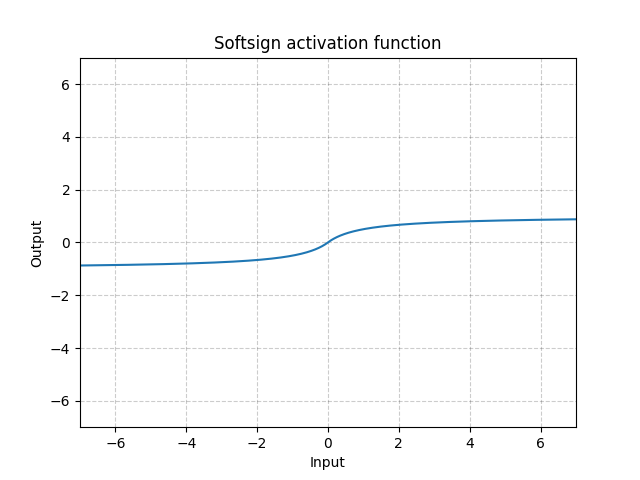
图 13: Softsign
它類似於S型函數,分別是它緩慢到達漸近線並(在某種程度)上減輕了梯度消失的問題。
Hardtanh - nn.Hardtanh()
\[\text{HardTanh}(x) = \begin{cases}
1, & \text{if} x > 1\\
-1, & \text{if} x < -1\\
x, & \text{otherwise}
\end{cases}\]
线性的值域 [-1, 1] 的范围可以使用min_val 和 max_val來调整
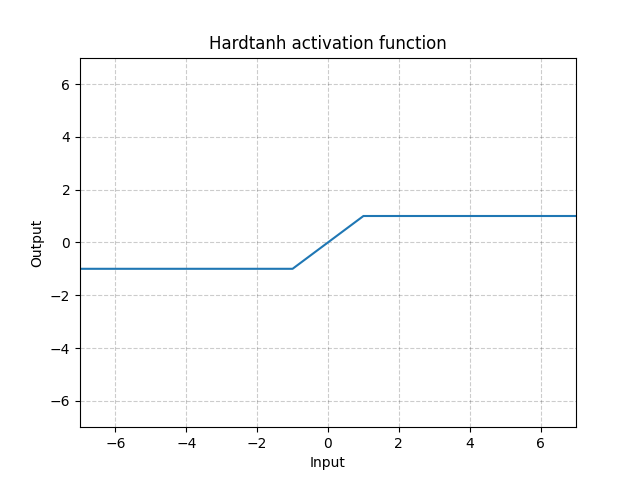
图 14: Hardtanh
它运行得很好,特别是当权重是保持在一个很小的值域。
下限值(Threshold) - nn.Threshold()
\[y = \begin{cases}
x, & \text{如果 $x > \text{threshold}$}\\
v, & \text{否则就}
\end{cases}\]
很少使用它,因为我们无法将梯度传播回来。这也是阻止人们在60年代和70年代对二进制神经元使用反向传播的原因。
Tanhshrink - nn.Tanhshrink()
\[\text{Tanh收缩形(Tanhshrink)}(x) = x - \tanh(x)\]
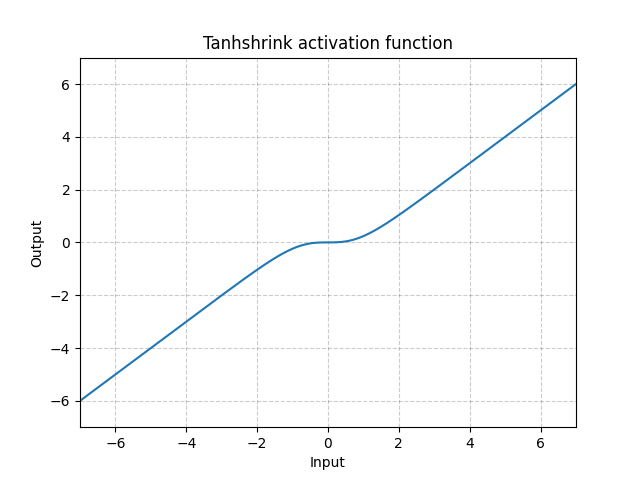
图 15: Tanhshrink
很少使用它,除了用在稀疏编码上来计算潜在变量的值。
Softshrink - nn.Softshrink()
\[\text{SoftShrinkage}(x) = \begin{cases}
x - \lambda, & \text{if} x > \lambda\\
x + \lambda, & \text{if} x < -\lambda\\
0, & \text{otherwise}
\end{cases}\]
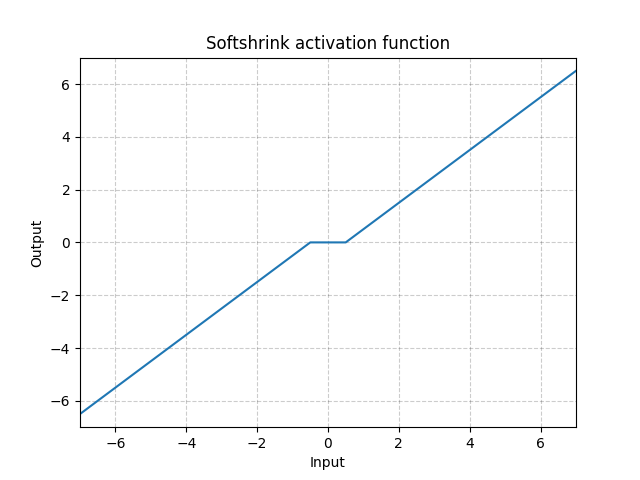
图 16: Softshrink
基本上就是把变量以一个恒量来收缩到达零,而强行它成为零,如果变量是接近零。你可以想它为 $\ell_1$ 标准的梯度的一个步。它也是Shrinkage-Thresholding Algorithm (ISTA)的迭代们中的一个迭代。但是它在标准神经网络中通常不用作为激活。
Hardshrink - nn.Hardshrink()
\[\text{HardShrinkage}(x) = \begin{cases}
x, & \text{if} x > \lambda\\
x, & \text{if} x < -\lambda\\
0, & \text{otherwise}
\end{cases}\]
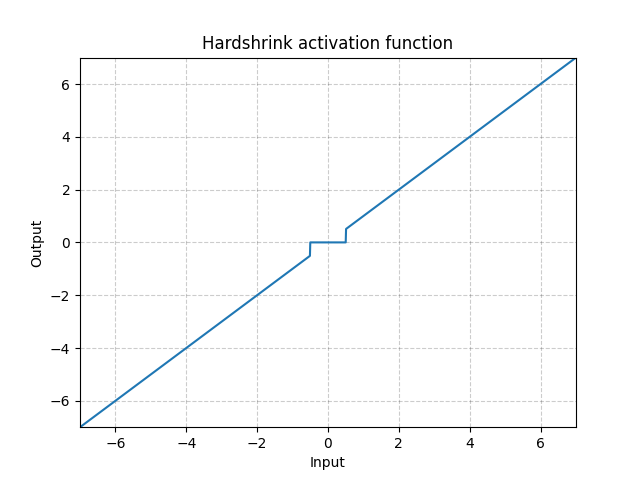
图 17: Hardshrink
除了稀疏编码,很少使用它。
LogSigmoid - nn.LogSigmoid()
\[\text{LogSigmoid}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right)\]
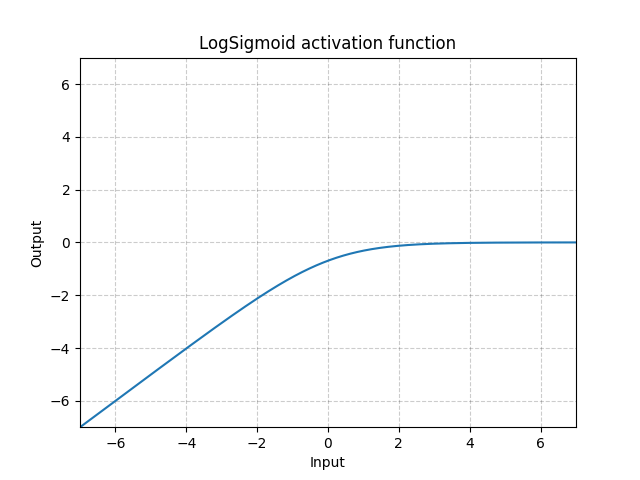
图 18: 对数式S型函数(LogSigmoid)
它主要用于损失函数,但用于激活的话就并不常见。
Softmin - nn.Softmin()
\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)}\]
它将数字转换为概率分布。
Soft(arg)max - nn.Softmax()
\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]
LogSoft(arg)max - nn.LogSoftmax()
\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right)\]
它主要用于损失函数,但对于激活来说就并不常见。
问答场节-激活函数
有关 nn.PReLU() 的问题
-
为什么我们想在所有频道中的$a$都有一样的值?
不同的频道会有不同的a。您可以将a用作每个单元的参数。它可以以特征图那样共享起来。
-
要可学习的$a$吗?是不是可学习的$a$是有利的?
你可以令$a$为可学习或令它锁定不变。 锁定不变做法的原因是确保它的非线性可以在负数区中给你一个非零梯度。 令$a$为可学习的可以令系统把非线性转为线性映射或整个截半(full retification)。对于某些应用,例如实现边缘检测器,无论边缘极性如何,它都可能很有用。
-
非线性度应该有多复杂才好?
理论上,我们想整个非线性函数以很复杂的方式来参数化,比如弹簧参数﹑切比雪夫多项式(chebyshev polynomial)﹑等等。参数化会是学习过程的一部份。
-
与系统中拥有更多單元相比,参数化有什么更好的优势?
这实际上取决于您想要做什么。例如,在低维空间中进行回归(regression )时,参数化就有帮助了。相反,如果你的任务是在高维度空间,如图像识辨,那就必须有非线性,而单调非线性会更好。 简而言之,您可以参数化所需的任何函数,但并不能带来很大的优势。
扭结相关问题
-
单扭结 VS 双扭结
双扭结是内置標度的。意思是如果输入层是能乘以2出来的(或信号幅度是能乘以2出来的),那输出就会完全不同。信息会在非线性中变得更大,所以你会得到完全不同的输出特性。如果你的函数是单扭结,那输出被乘以2,那输出也都会乘以2。
-
一个有扭结的非线性激活和一个平滑的非线性激活有什么分别。为什么/什么时候用那一个好?
这是规模等方差的问题,如果扭结得很过头,你就对输入乘以2,那输出就如被乘以2那样了。如果你有一个平滑的过程,比方这样说,如果你对输入乘以100,那输出看上去就如扭结得很过头,因为平滑的部份是收缩了100倍。如果将输入除以100,那扭结就会变成一个非常平滑的凸函数。所以,改变输入的标度,你就改变激活单元的行为。
有时这会是一个问题。比如,当训练多层神经网络时和您有个两层,如同一层在另一层后。你的非线性是受标量影响,那你的网路在输入中就没有选择权重矩阵的大小,因为这会完全改变整个行为。
解决此问题的一种方法是在每层的权重上设置一个强而有力的标度,以便您可以标准化所有层的权重,例如批量标准化。所以那个会走入单元的可变性就变成恒量。如果你固定好标度,那系统就不会有任何方法去选择非线性的那一部份会用双扭结函数系统。这会是一个问题如果这个固定部份变得更线性。比如,S型函数就会变得更线性和接近零,而且所以批量标准化的输出(接近0)就不会有活性的”非线性”。
还是不完全地明白为什么单扭结函数在深度网路中好用。它应该是因为标度等方差属性。
在soft(arg)max函数中的温度系数
-
什么时候使用温度系数,为什么使用温度系数?
在某种程度上,温度系数对于新输入的权重是多余的。如果你有加权总和输入到你的softmax,那以权重们的大小来说$\beta$参数就是多余了。
温度控制着输出的分布有多硬。当$\beta$是非常大,它就会变得接近1或零。当$\beta$是小,它就会很软。当$\beta$的极限是等于零时,它就如平均那样。当$\beta$去到无限制,它的行为就如argmax。所以如果你在softmax前,有正常化中一些软的,调一调这个参数能令你控制硬度。 有时,你可以从一个很细的$\beta$开始,那样你就有一个运作得很好的梯度下降,在运行后,如果你想要在你的注意机制中有一个很硬的决定,你提高$\beta$。所以,你就能把决定磨尖。这个技巧叫退火。在和一些高等技巧混合起来的话就会很有用,比如自我注意机制。
损失函数
Pytorch也写入了很多损失函数。这里我们会说一说它们。
nn.MSELoss()
这个函数在输入$x$和目标y中给予均方误差(mean squared error,或MSE,又叫L2平方规范)。也称为L2损失。
如果我们在用$n$个样本的小批量,那这里就有$n$个损失,一个损失就对应批量中一个样本。我们可以令损失函数中的损失以向量方式来保存或降低函数中的损失。
如果不降低,英文unreduced(即设置reduction='none'),而损失就是
那个$N$就是批量的大小,$x$和$y$是任意大小的张量,每个张量总共n个。
降低选项在下方(注意默认值为reduction='mean')。 mean意思是平,sum是总和。
这个总和计算还是对所有东西总和起来,然后除以$n$。
这个除以$n$计算可以避免,如果设定了reduction = 'sum'的话。
nn.L1Loss()
这测量输入$x$中每个元素和目标$y$(或实际输出和所需输出)之间的平均绝对误差(MAE)。
如果不降低 (i.e. 设 reduction='none'),不降低英文是unreduced, 而损失就是
, 那个 $N$ 就是批量的大小,$x$和$y$是任意大小的张量,每个张量总共n个。
它也有'sum'和'mean'的降低reduction选项,sum意思总和,而mean意思是平均,这些都和 nn.MSELoss() 相似。
用例: L1损失(L1Loss)比L2损失(L2Loss)更不受异常值和噪声影响。在L2中,异常值和噪声带来的错误会被平方,所以损失函数会对这些异常值更敏感。
问题: L1损失不是在底部零的位置不是可微的。我们要小心处理它的梯度(即softshrink)。这启发接下来的L1损失的平滑版,叫SmoothL1Loss。
nn.SmoothL1Loss()
这个函数用l2损失,如果是绝对元素误差(element-wise error)低于1和l1的话,否则(otherwise)。
\(\text{loss}(x, y) = \frac{1}{n} \sum_i z_i\) , 其中 $z_i$ 由
\[z_i = \begin{cases}0.5(x_i-y_i)^2, \quad &\text{if } |x_i - y_i| < 1\\ |x_i - y_i| - 0.5, \quad &\text{otherwise} \end{cases}\]这也有 降低 选项。
这是由 Ross Girshick (快速版R-CNN,Fast R-CNN)提倡。当把它以目标函数来使用,那个平滑版L1损失(Smooth L1 Loss)也被称为胡伯损失(Huber Loss)或弹性网路。
用例: 这是比均方误差损失(MSELoss)对异常值更不敏感,而且底部是很平滑。这个函数经常地被用在计算机视觉来防止受异常值影响。
问题: 这个函数是有标度(0.5就是了,上方的函数就用0.5了)。
计算机视觉L1 vs. L2
当我们有很多不同的$y$们时在做出预测:
- 如果我们用均方误差损失(英文MSE,或L2损失),结果就是平均所有$y$,意思就是在CV中,我们就有一个模糊图片。
- 如果我们用L1损失,那个能最小化L1距离的$y$值就是中等,也就是图像不模糊,但注意这个中等是很难在多重维度中被定义出来的。
用L1的话,结果就是在预测中有更锐利的图片。
nn.NLLLoss()
当去训练c个类的分类问题时,就用负对数似然损失(negative log likelihood loss )。
注意下这个,数学上,NLLLoss 应该是对数似然,但Pytorch不会强行这样。所以效果是令所需的组件尽可能大。
那个不降低(i.e. 把 :attr:reduction设定为 'none',reduction是降低,而none是无),损失就可以被形容为这样:
,其中 $N$ 是批量大小。 weight=权重, ignore_index= 要无视的号数
如果reduction不是 'none',英文'none' (如果默认值,那是’平均数,英文'mean'),之后
\(\ell(x, y) = \begin{cases} \sum_{n=1}^N \frac{1}{\sum_{n=1}^N w_{y_n}} l_n, & \text{if reduction} = \text{'mean';}\\ \sum_{n=1}^N l_n, & \text{if reduction} = \text{'sum'.} \end{cases}\) if reduction=’mean’; #中文是如果降低=’‘平均数”; if reduction=’mean’; #中文是如果降低=’‘总和”;
这个损失函数有一个可选的引数weight,中文是权重,这能够用一个一维的张量传入到这里来对每个类来分配权重。当面对一个不平衡的训练集时是十分有用的。
权重和不平衡的类:
当每个类别或类的频率是不一样时,权重向量是十分有用。例如,普通流感的发生频率要远高于肺癌。那我们就能简单地因应一些只有小样本的类别来提高权重。
相反,除了设定权重外,都是最好去均衡好训练频率,那梯度就更好地被利用。
去均衡训练时的类,我们放每一个类的样本在不同的缓冲。然后在每一个缓冲区中选择相同数量的样本来生成对应每一个缓冲区的小批量。当一个比较小的缓冲用完它的最后一个样本时,我们就重头开始用那个较小的缓冲,直到比较大的类的每一个样本都被用上。这方法令这些循环式缓冲区有一个一样的频率。我们不应该为了均衡频率,而走那条容易的路,就是那条为了均衡频率,而没有用大部份的类们的所有的样本。不要把数据扔在地上!
去均衡训练时的类,我们放每一个类的样本在不同的缓冲。然后在每一个缓冲区中选择相同数量的样本来生成对应每一个缓冲区的小批量。当一个比较小的缓冲用完它的最后一个样本时,我们就重头开始用那个较小的缓冲,直到比较大的类的每一个样本都被用上。这方法令这些循环式缓冲区有一个一样的频率。我们不应该为了均衡频率,而走那条容易的路,就是那条为了均衡频率,而没有用大部份的类们的所有的样本。不要把数据扔在地上!
为了了解这个方案,我们回到医学院的例子:学生在罕见疾病上花的时间与他们在常见疾病上花费的时间一样多(或许是更多的时间,因为罕见疾病通常是更复杂的疾病) 。他们学会适应所有病的特征,然后更正它以了解哪些是罕见的。
nn.CrossEntropyLoss()
这个函数包含nn.LogSoftmax 和nn.NLLLoss在单一个类。这个合二为一令正确分数的类变得有多大得有多大。
两个函数合起来的原因是为了梯度计算的数值稳定性。当softmax后的值是接近一或零,用个对数就一是给零或负$-\infty$。而对数的斜率接近0就是接近$\infty$,令到导致反向传播的中间步骤出现数值问题。当两个函数是合二为一时,梯度就会饱和,所以最后我们得到一个合理的数字。
每个类的输入均期望为非标准化分数。
损失可描述为:
\[\text{loss}(x, c) = -\log\left(\frac{\exp(x[c])}{\sum_j \exp(x[j])}\right) = -x[c] + \log\left(\sum_j \exp(x[j])\right)\]或在weight这个引数会被指定为:
或在weight这个引数会被指定为:
交叉熵损失的物理学上的解释,是有关于KL散发(KL divergence,全名Kullback–Leibler divergence),这是当我们用来测量两个分布的散发。这里,那个(准)分布们是为x向量(预测)来代表和目标分布(一热向量one-hot vector以一个0代表错误的类,而1 代表正确的类)。
数学上,
\[H(p,q) = H(p) + \mathcal{D}_{KL} (p \mid\mid q)\]数学上, \(H(p,q) = - \sum_i p(x_i) \log (q(x_i))\) 就是交叉熵(两个分布之间), \(H(p) = - \sum_i p(x_i) \log (p(x_i))\) 是熵,而\(\mathcal{D}_{KL} (p \mid\mid q) = \sum_i p(x_i) \log \frac{p(x_i)}{q(x_i)}\) 是KL散发。
nn.AdaptiveLogSoftmaxWithLoss()
这是一个有效的对应大量的类的softmax的 softmax 近似法(比如:数百万类)。它实现了一些技巧来提高计算速度。
该方法的详细信息在Efficient softmax approximation for GPUs 作者: Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, Hervé Jégou.
📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Jonathan Sum(😊🍩📙)
13 April 2020