The Truck Backer-Upper

设定

任务的目标是建造一个自主学习控制器（self-learning controller）用以操控驾驶货车，并从任意起点倒库至装载码头。

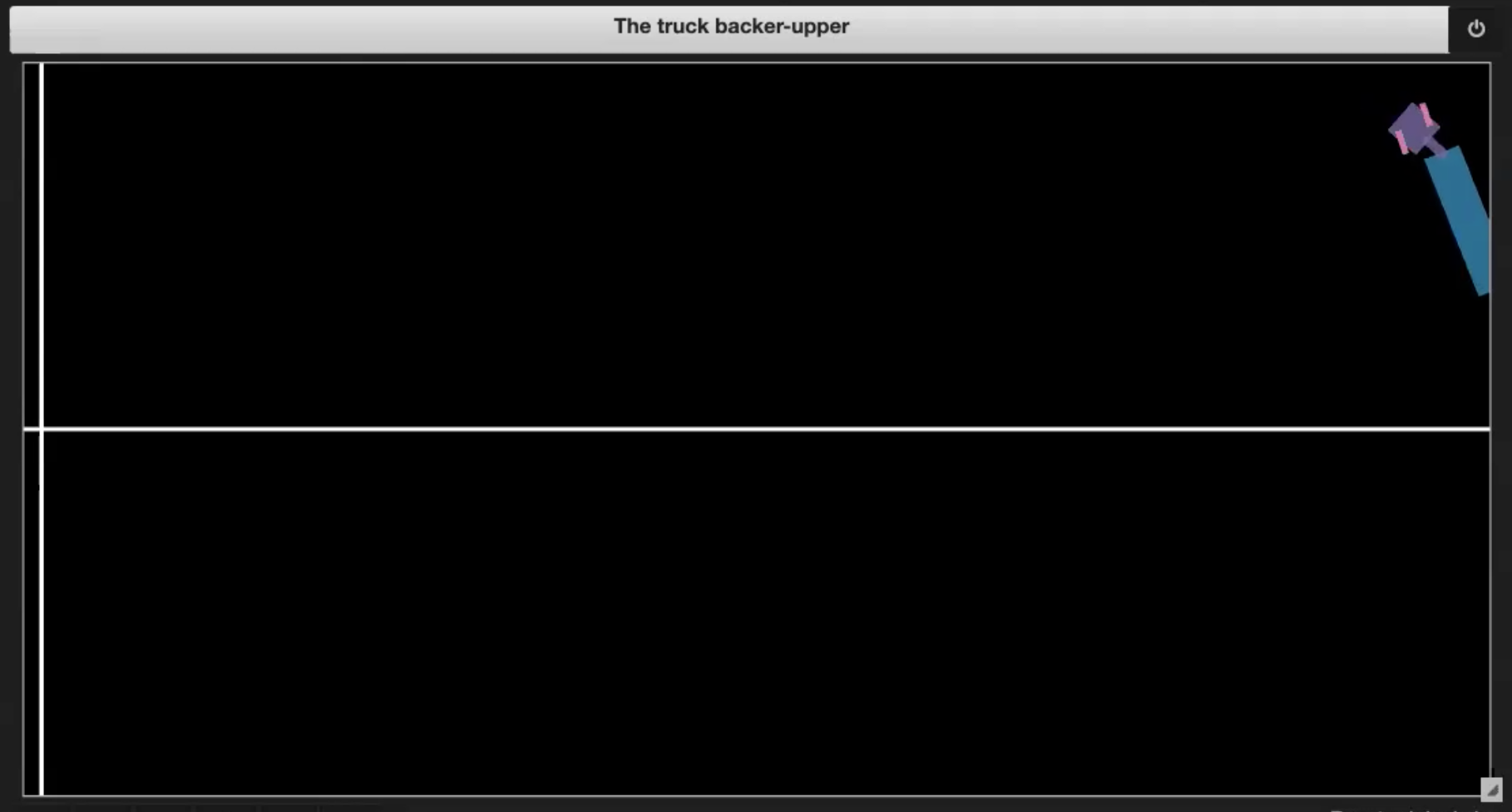
注意如图一所示，任务只允许倒车。

图1: 货车、拖车，和装载码头

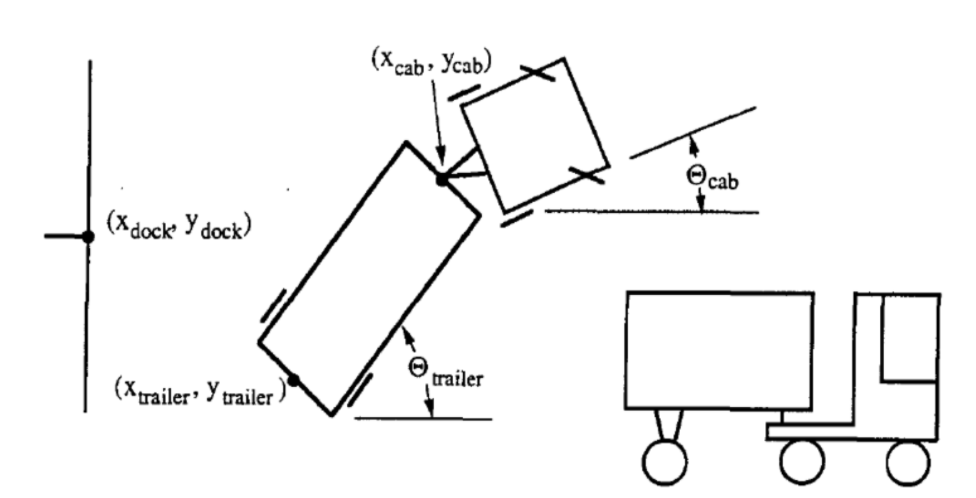货车的六个参数的状态：

• $\tcab$: 货车的角度
• $\xcab, \ycab$: 轭的直角坐标（拖车前部）
• $\ttrailer$: 拖车角度
• $\xtrailer, \ytrailer$: 拖车（背部）的直角坐标

控制器的目标是在货车倒行一小段固定距离后，在时刻$k$选择合适的角度$\phi$。目标实现依靠两点：

1. 拖车背部与装载码头的墙面平行，如$\ttrailer = 0$。

2. 拖车背部($\xtrailer, \ytrailer$)尽可能接近点($x_{dock}, y_{dock}$)，如上图所示。

更多参数与图示

图 2: 参数的图示

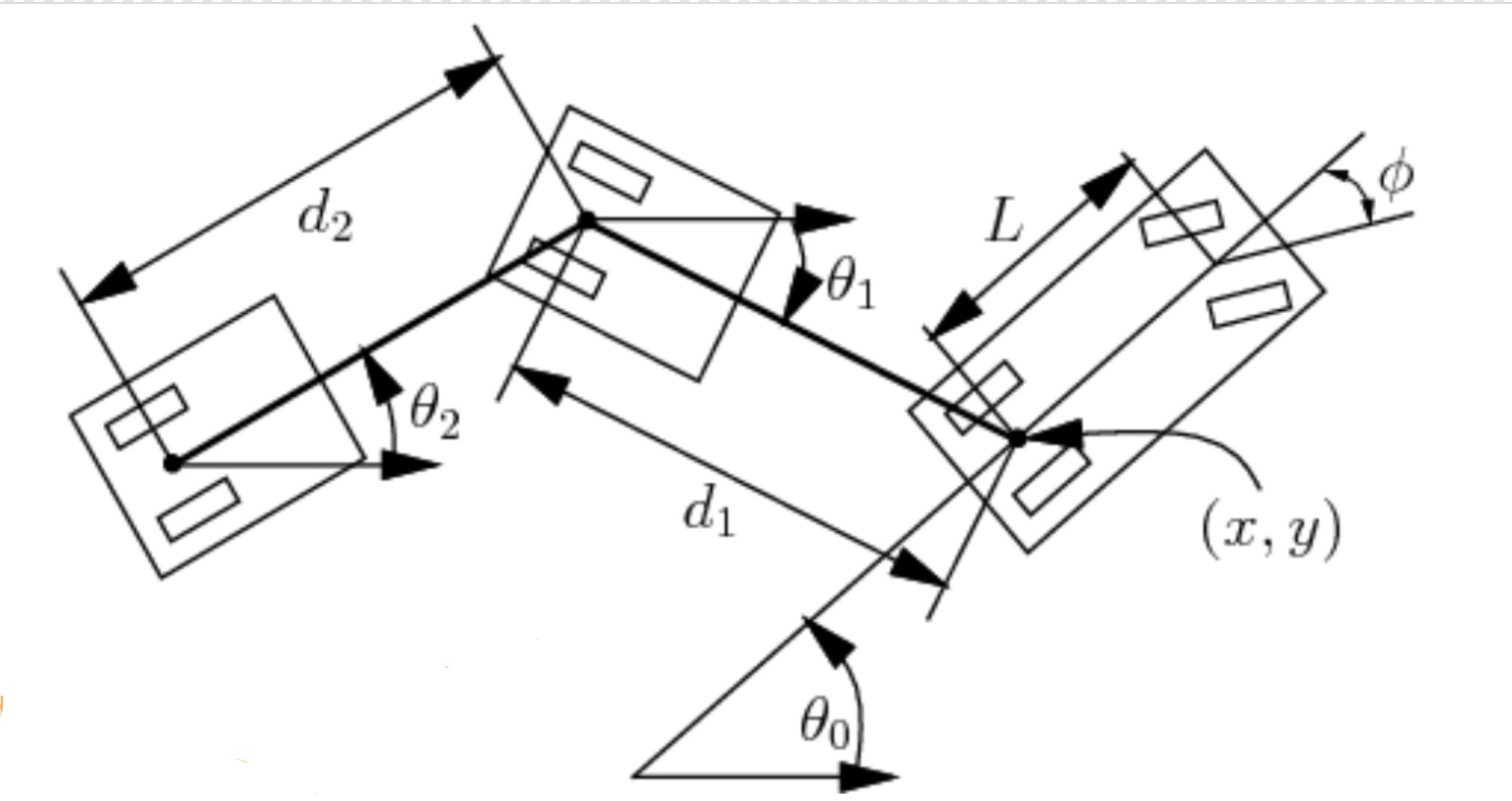在这一部分，我们还考虑到一些图二中的参数。

假设货车车长是 $L$、货车与拖车的间距是$d_1$，拖车车长为$d_2$，等等。我们可以计算角度与位置的变化： \(\begin{aligned} \dot{\theta_0} &= \frac{s}{L}\tan(\phi)\\ \dot{\theta_1} &= \frac{s}{d_1}\sin(\theta_1 - \theta_0)\\ \dot{x} &= s\cos(\theta_0)\\ \dot{y} &= s\sin(\theta_0) \end{aligned}\)

此处$s$表示正负速度，$\phi$表示负的驾驶角度。

现在我们可以只用四个参数表示状态：$\xcab$、$\ycab$、$\theta_0$，和$\theta_1$。

这是因为长度参数已知，并且$\xtrailer, \ytrailer$由$\xcab, \ycab, d_1, \theta_1$决定。

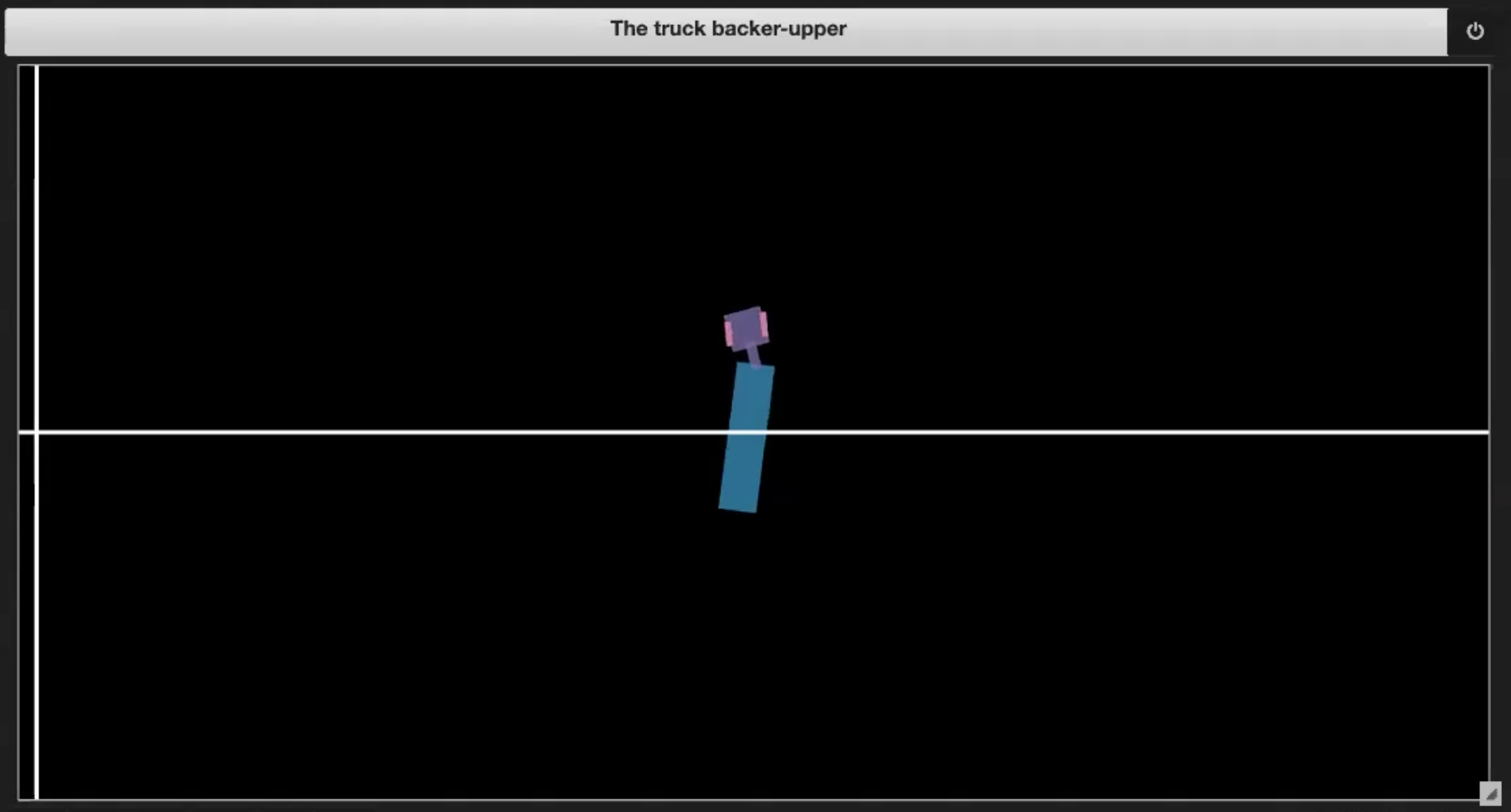
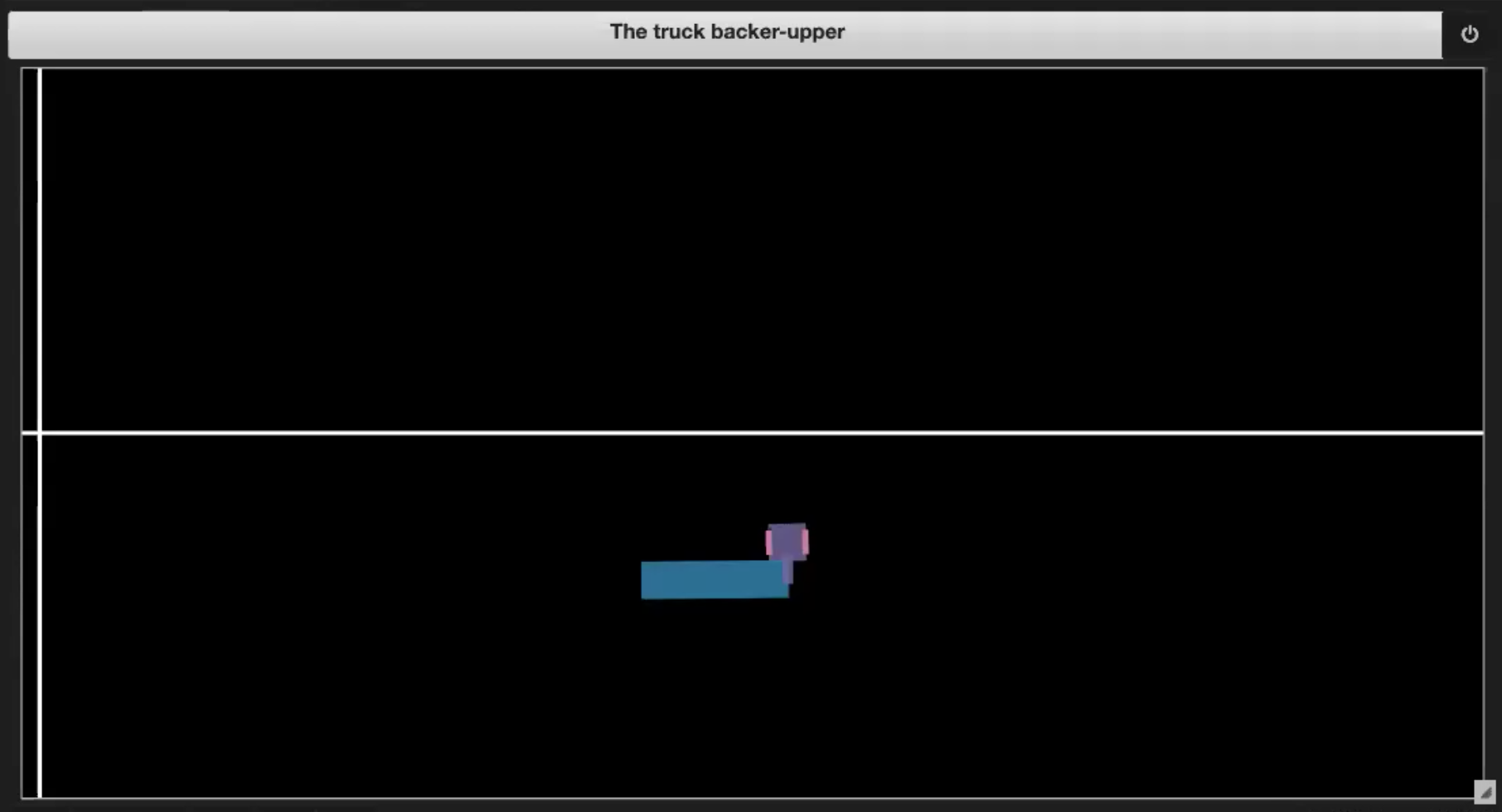
在深度学习文件库里的Jupyter Notebook中，我们有一些样本环境，如图3.(1-4)所示：

图 3.1: Sample plot of the environment	图 3.2: Driving into itself (jackknifing)
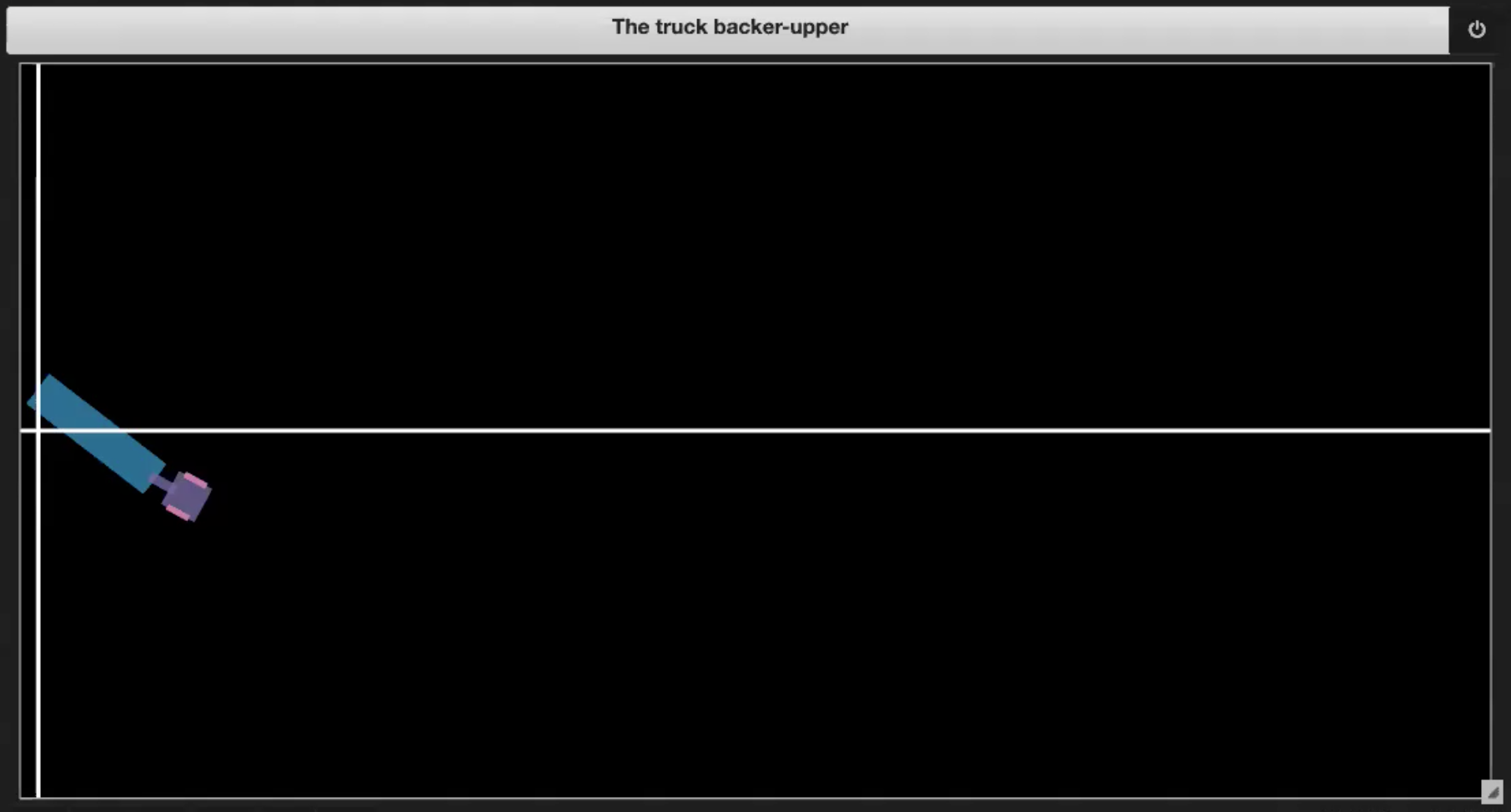图 3.3: Going out of boundary	图 3.4: Reaching the dock

在每时刻$k$，驾驶信号的值域是从$-\frac{\pi}{4}$到$\frac{\pi}{4}$，货车接收到信号后以相应的角度倒退。

以下几种工作程序可以结束的情况：

• 如果货车车头折叠，如图3.2所示

• 如果货车驶过边界，如图3.3所示

• 如果货车到达码头，如图3.4所示

训练

训练过程由两个阶段组成：（1）训练神经网络成为一个货车和拖车动力的模拟器；（2）训练神经网络控制器用以控制货车。

图 4: 概览图

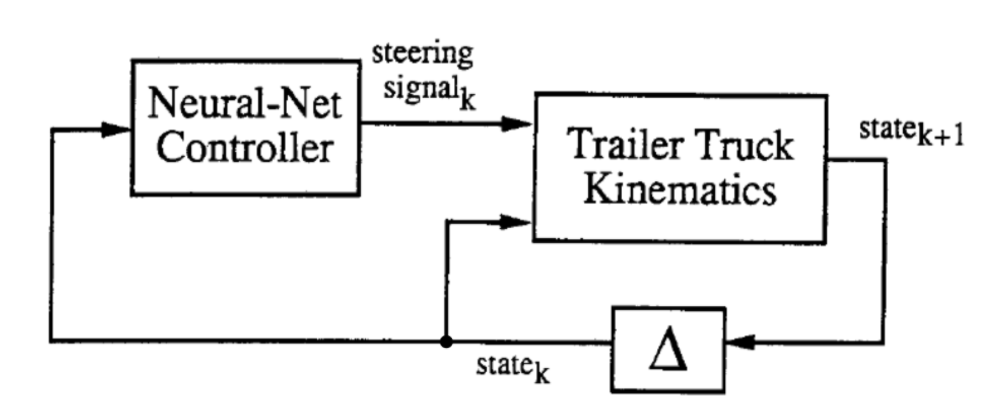如上图所示，在抽象图中，两个方块为两个即将被训练的网络。在每一时刻$k$，”拖车货车动力”或称作模拟器，用六维状态向量和控制器生成的驾驶信号，并在时刻$k + 1$生成一个新的六维状态。

模拟器

模拟器用当前时刻的位置($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$)和驾驶方向$\phi^t$作为输入，并输出下一时刻的状态($\tcab^{t+1}$,$\xcab^{t+1}, \ycab^{t+1}$, $\ttrailer^{t+1}$, $\xtrailer^{t+1}$, $\ytrailer^{t+1}$)。它由一个带ReLu激活函数的线性隐藏层和一个线性输出层组成。我们用MSE作为损失函数并通过SGD训练模拟器。

图 5:训练神经网络控制器

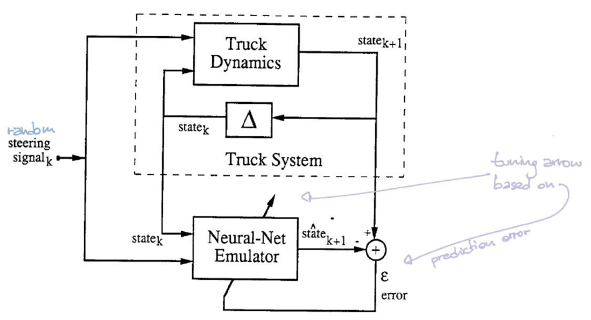在这个设定里，模拟程序可以用已知的当前时刻的位置和驾驶角度告诉我们下一步的位置。所以，我们不需要一个神经网络来效仿模拟程序。然而，在更复杂的系统中，我们可能无法接触到系统的底层公式，也就是说我们没有一个漂亮形式可以计算宇宙法则。我们可能无法观测记录驾驶信号和对应路径的序列的数据。这种情况下，我们想要训练一个神经网络来模仿这个复杂系统的动态。

为了训练模拟器，我们需要仔细研究Class truck中的两个重要的方程。

第一个是step方程，在计算后它会给出货车的输出状态。

def step(self, ϕ=0, dt=1):

    # Check for illegal conditions
    if self.is_jackknifed():
        print('The truck is jackknifed!')
        return

    if self.is_offscreen():
        print('The car or trailer is off screen')
        return

    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()

    # Perform state update
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

第二个是state方程，它给出货车的当前状态。

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

我们首先生成两个list。我们通过加入随机生成的驾驶角度ϕ和运行truck.state()得到的货车的初始状态生成输入list。然后我们通过加入由truck.step(ϕ)计算得到的火车输出状态生成输出list。

现在我们可以训练模拟器：

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)

    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)

    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()

    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

注意torch.randperm(len(train_inputs))给我们一个随机的索引排列，其值域从$0$到训练输入的长度减$1$。索引排列后，每次在索引i从输入list选出ϕ_state 。我们通过模仿方程，其包含一个线性输出层，输入ϕ_state，然后得到next_state_prediction。注意模拟器是一个神经网络，其定义如下所示：

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

此处我们用MSE计算下一状态的真实值和下一状态的预测值之间的损失函数，下一状态的真实值来自索引i的输出list，对应来自输入list的ϕ_state的索引。

控制器

根据图5，方块$\matr{C}$代表控制器。它输入进当前状态并输出驾驶角度。方块$\matr{T}$（模拟器）输送进状态和角度，产生下一状态。

Fig. 5: 状态转换流图示

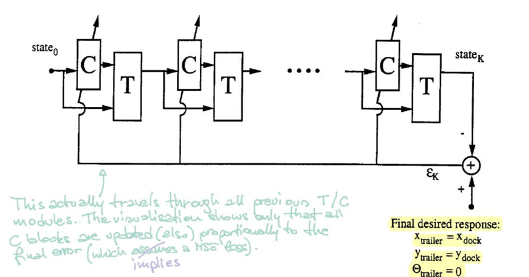*注：状态穿过所有之前的$\matr{T}/\matr{C}$模块。本图只显示所有方块$\matr{C}$按比例更新到最终误差（意指MSE损失函数）。

为了训练控制器，我们从任意初始状态开始并重复过程($\matr{C}$和$\matr{T}$)直到拖车与码头平行。误差由对比拖车位置与码头位置计算得出。然后我们用向后传播得到梯度并且用SGD更新控制器的参数。

详解模型结构

下图为($\matr{C}$, $\matr{T}$)过程的详细图解。我们用一个状态（六维向量）乘以可调节的权重矩阵，得到25个隐藏单元。然后将它传送到另一颗可调节的权重矩阵以获得输出（驾驶信号）。相似的，我们通过两层输入状态和角度$\phi$（七维向量）来产生下一步的状态。

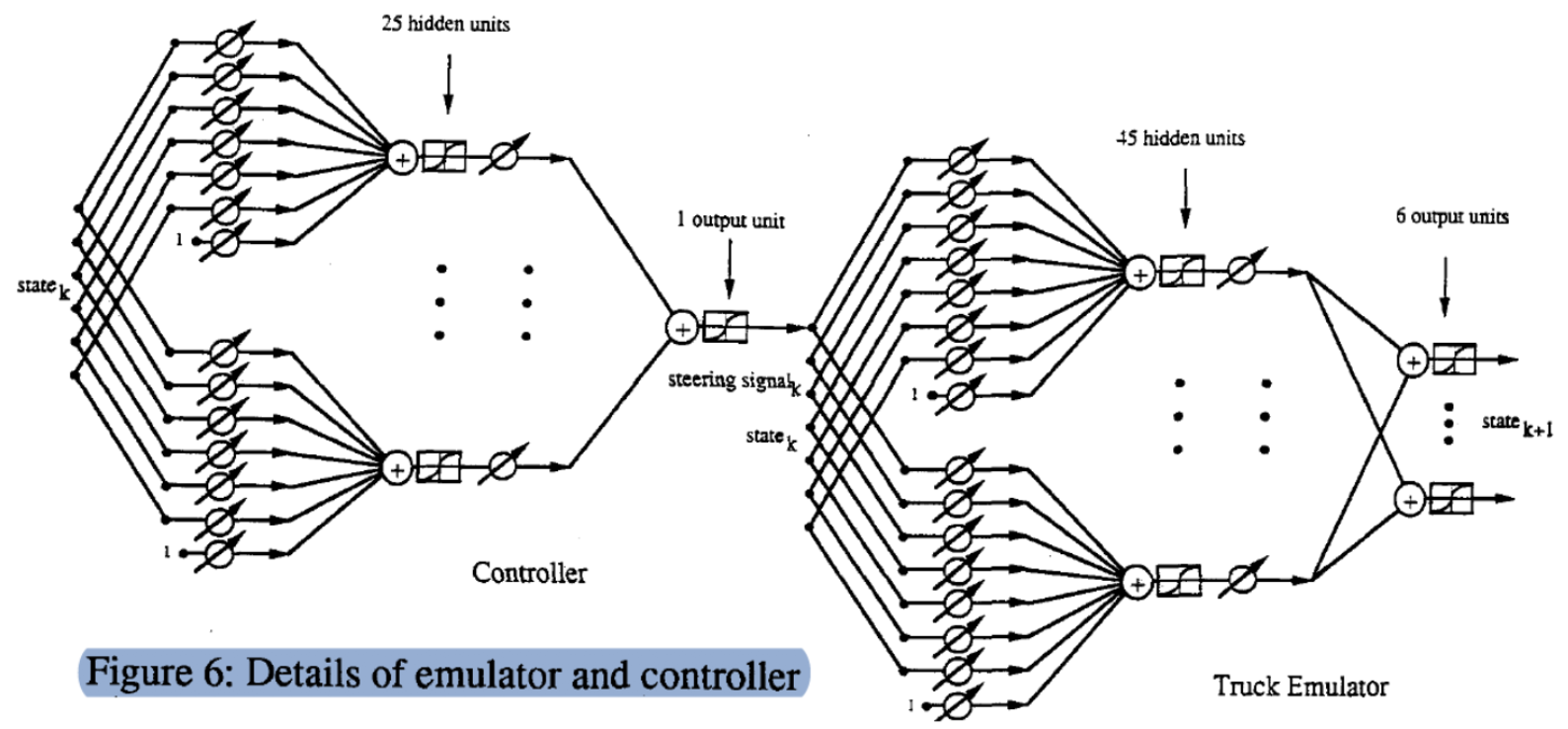
为了更好地理解，我们展示了准确的模拟器的执行过程：

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

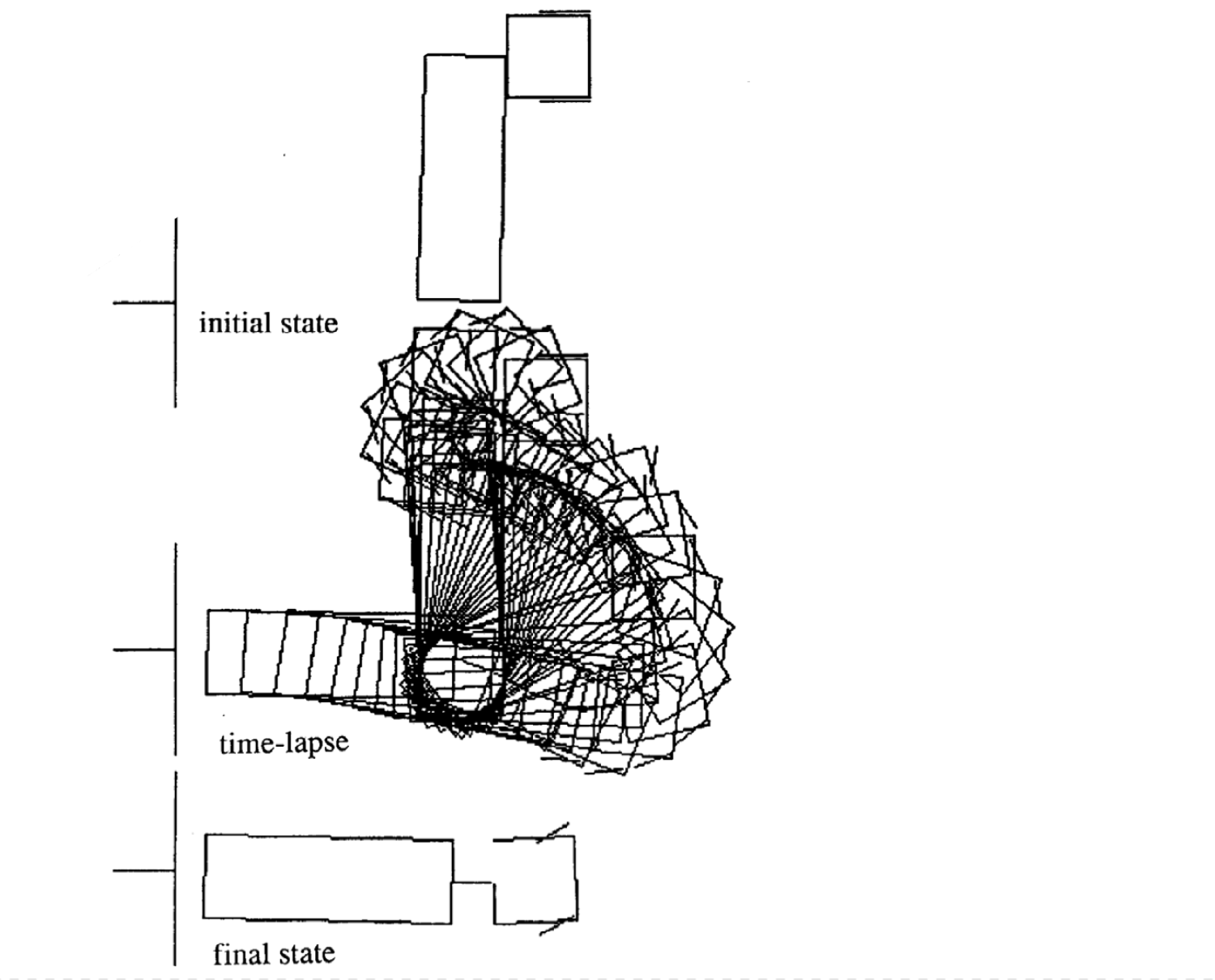
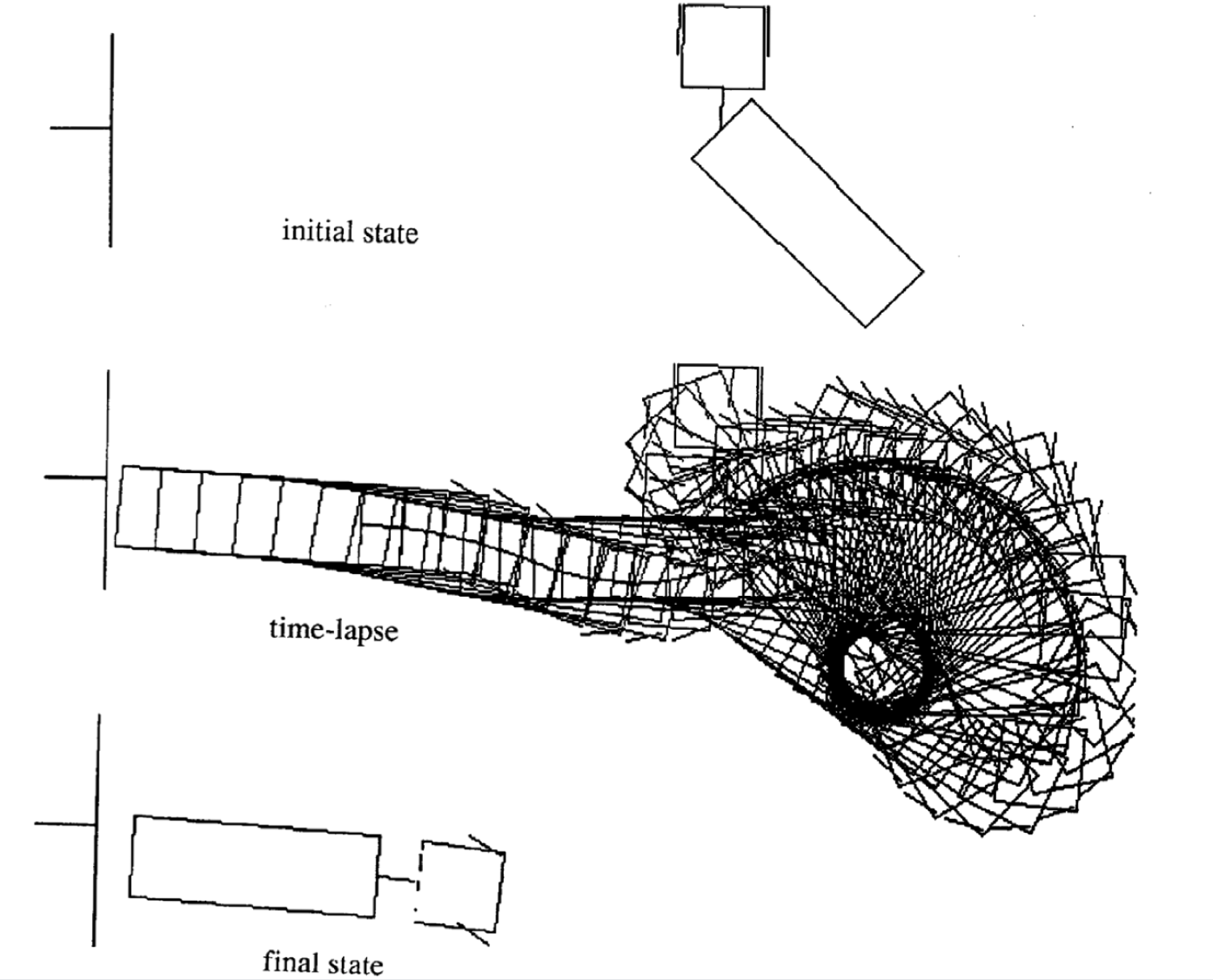
运动的例子

以下是四种不同初始状态的运动的例子。注意每种例子的时间步数是不一致的。

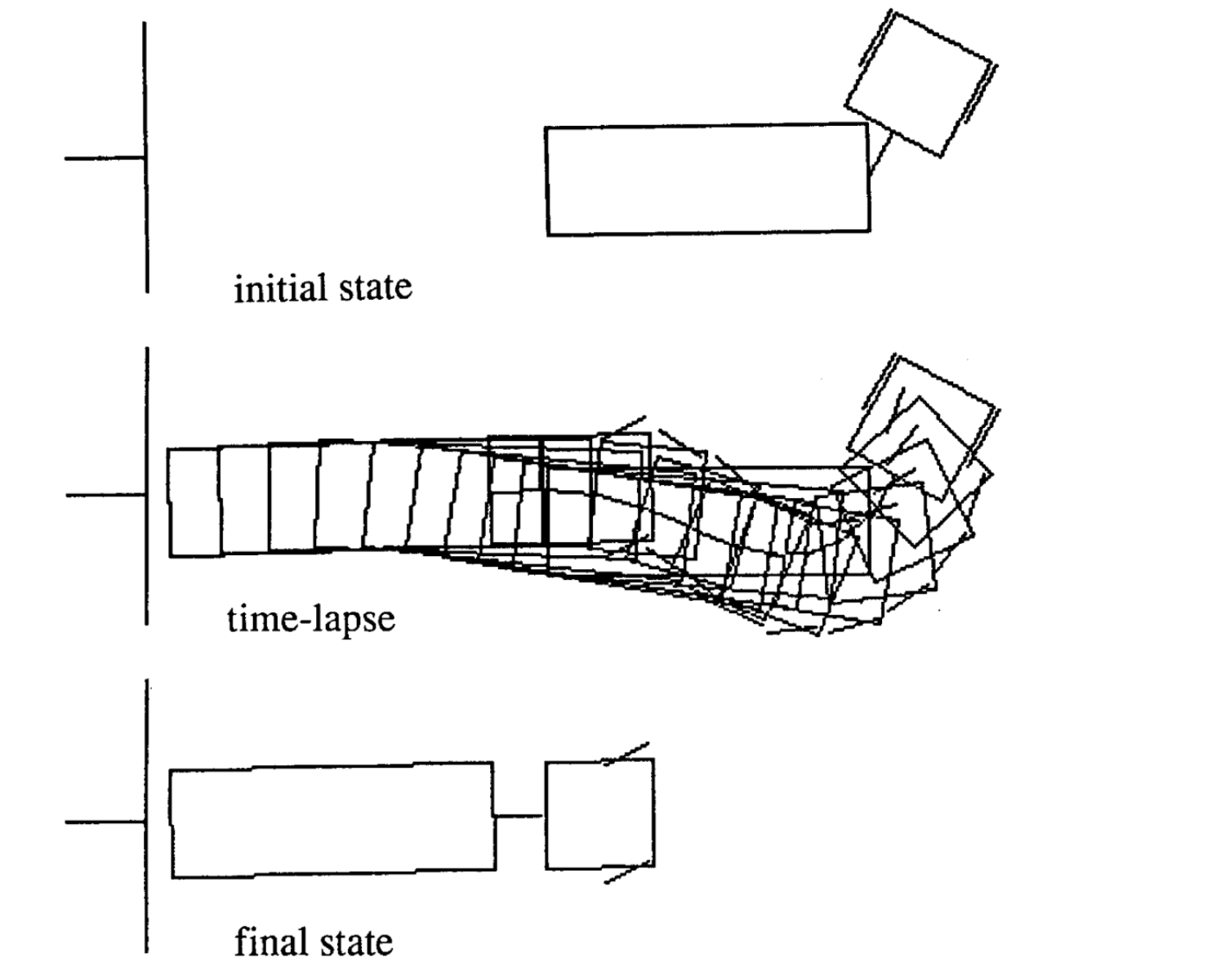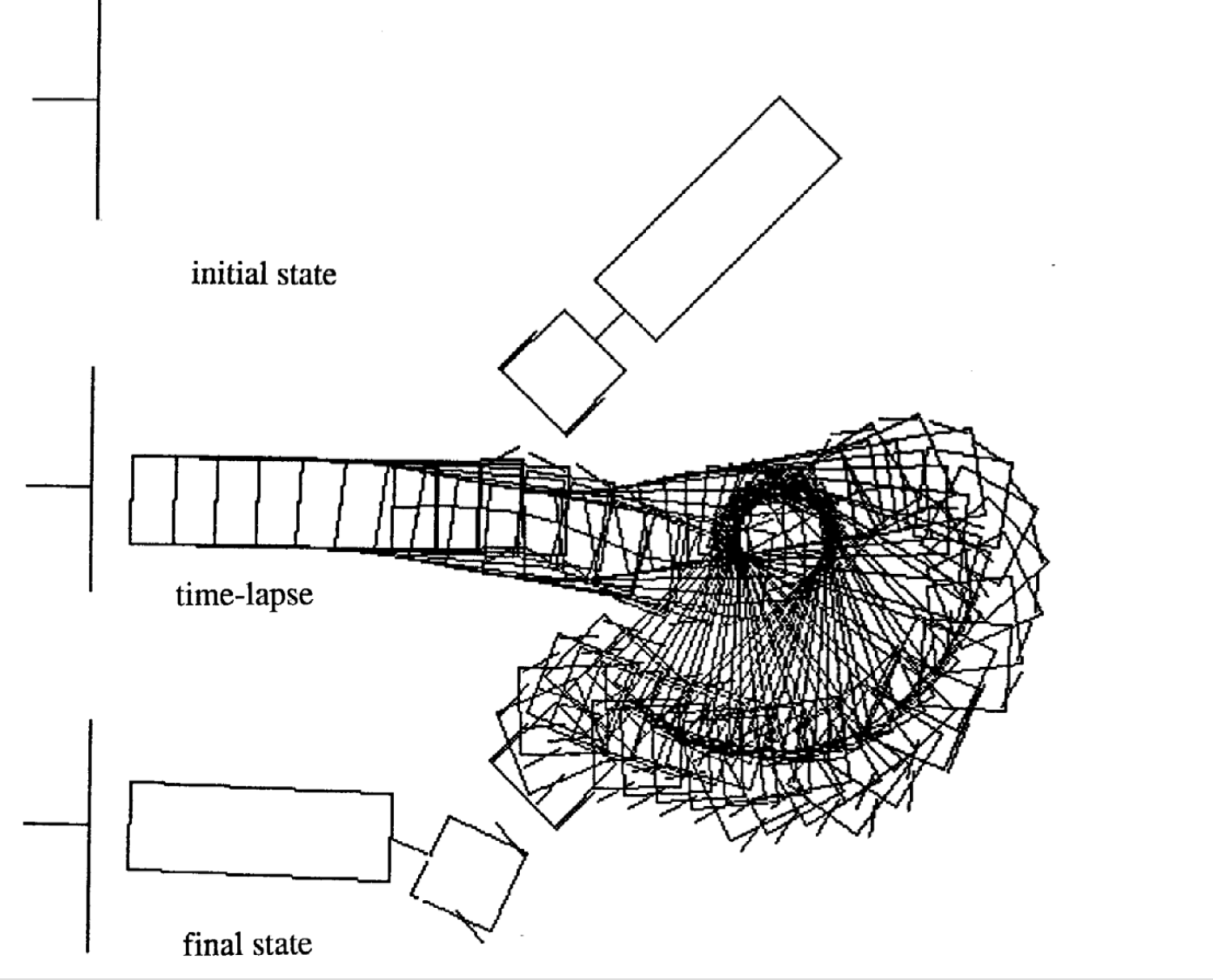补充资料：

完整的工作demo可以查看：https://tifu.github.io/truck_backer_upper/。

也请查看完整代码：https://github.com/Tifu/truck_backer_upper。