自我监督学习-前置任务

监督方法的成功故事: 前置训练

在上十年，一个用在许多不同的计算机视觉问题上的主要成功秘诀就是对ImageNet分类进行监督学习来学习视觉的「表示」。而且在没有大量标记了的数据时，使用这些学习到的表示，或模型中学习了东西的权重都作为其他计算机视觉任务的初始化部分，这都是成功秘诀之一。

相對地，取得ImageNet这样大小的数据集的注解是超花时间和昂贵。比如:ImageNet标记一千4百万张图就花了22年人类年。

因为这样，社区就找下别的标记方法，比如社交媒体图片的主题标签(hashtags)，GPS位置，自我监督的方法，也就标签是数据样本本身的属性。

但更重要的问题就在别的标记法中出现了:

到底我们真正需要标记多少图片才够呢?

• 如果我们以物件类别分类和边界框式分类，那就有1百万张图片。
• 现在，如果边界框式分类的框被松开的话，那图片数量就跳跃到1400万(大约)。
• 相反，如果我们考虑用上互联网所有图像，就后方加多五个零吧。
• 而且，之后就要处理图片背后包含的数据，那就更要求其他感觉到这些的数据的输入来捕获或理解这些的数据。

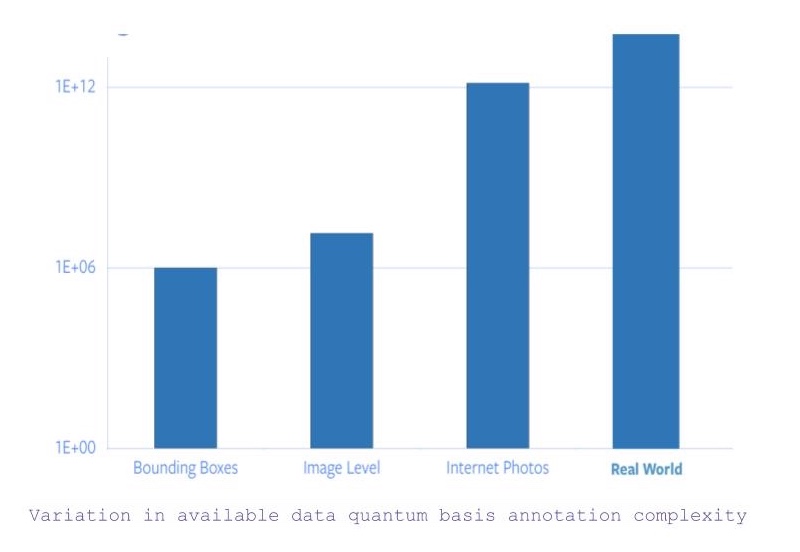
图 1:注释可用数据的总额基础复杂度的变化

所以，以事实上ImageNet对图片的注释就花了22个人类年，那标签网上所有的图片就是不可行的。

稀有概念的问题 (长尾巴问题)

就是了，大部份的图片对应很少标签，同时那里存在很大量的标签对应很少量的图片。所以，对这大量数据，如长尾巴一样很大很长，去标签就是最标签如天文数字一样多的数据一样。[忘记这个多余的短语吧]:<>(因为种类的分布就是这样的)。

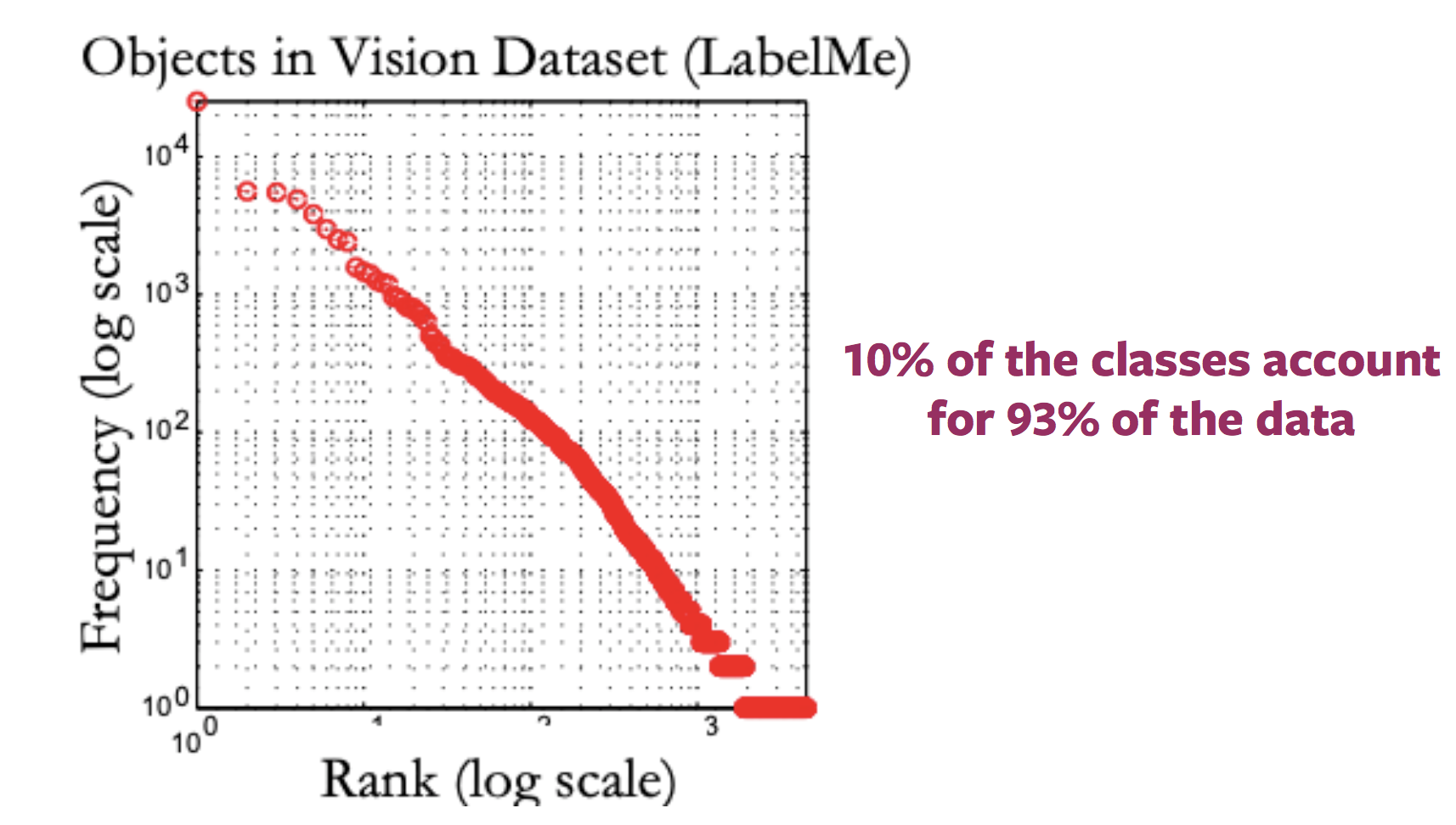
图 2: 标签了所有可用图片的分布的变化

不同领域的问题

当后期工作中用上的图片是属于和前期工作完全不同的领域时，这个ImageNet前置训练和微调的方法在后期工作就会变得更模糊不稳定的，例如医学图片。加上，用ImageNet中大量的数据集在，完全不同领域的工作的前置训练，那就不太可行。

到底什么是自我监督学习？

两种方法去定义自我监督学习

• 基础监督学习的定义，即是这样，如果网路是以监督学习方式来运行，标签是以半自动方式来取得，而不是人类输入说出是什么标签的话。预测问题，也就是数据一部份是隐藏，而数据另一部份是可见。所以，目标就是去预测隐藏了或隐藏部份的属性。

到底自我监督学习对于监督学习和无监督学习来说有什么不一样呢?

• 监督学习的工作包括预先标签工作(而且一般都是人类提供的)，
• 无监督学习就只有数据样本，而没有任何监督或标签﹑正确输出。
• 自我监督学习就由给予数据样本时就同时输出标签或给予数据样本的一部份时就同时输出标签。

自然语言处理中的自我监督学习

Word2Vec(文字转成向量)

• 给予用来输入的句子，那工作就包括预测句子中遗漏的单词，也就是故意地去掉一些字来实现前置任务。
• 所以，标签们的集合就会变成字典中所有可能有的文字，加上，正确的标签是句子中被删掉的字。
• 所以，可以用正常的梯度方式来训练网路来学习文字式的表示。

为什么用自我监督学习呢?

• 自我监督学习只要观察不同数据部份如何相互作用就能学出数据中的表示。
• 从而就可以不用去标签如天文数字那样多的数据。
• 加上，可以看出不同东西却只是一个单独数据的不同形式。

加上，可以看出不同东西却只是一个单独数据的不同形式。

一般来说，用上自我监督的计算机视觉做法就是包括以下两种工作，前置任务和真实工作(后期)。

• 真实的(后期)工作(后期)可以是任何分类工作或检测物体工作，有足够的标签过的数据样本。
• 前置任务包括自我监督学习工作以解决学习视觉看到的表示，这自我监督学习目标是使用学习了的表示或由过程中取得的模型权重，然后用这些表示来用在后期工作。

建立前置任务

• 用在计算机视觉问题的前置任务，这工作可以由图片和视频﹑图片或视频建立。
• 在每个前置任务中，就是一部份是可见的数据和一部份数据是隐藏不可见的，同时工作是预测隐藏不可见的数据或隐藏不可见的数据的属性。

前置任务示例：预测图像中的九宫格中一格的相对位置

• 输入:2个图片，也就是九宫格中的两个格，一个格是固定的，另一格是想知道相对位置的那格。
• 给予2个格(图片)，网路要根据其中一个固定的格的位置来预测另一个格的位置，这个格就是我们想要查询其相对位置的格。
• 给予2个格(图片)，网路要根据其中一个固定的格的位置来预测另一个格的位置，这个格就是我们想要查询其相对位置的格。
• 而且，这种工作标签可以根据固定的格来用一个决定出另一个格的位置。

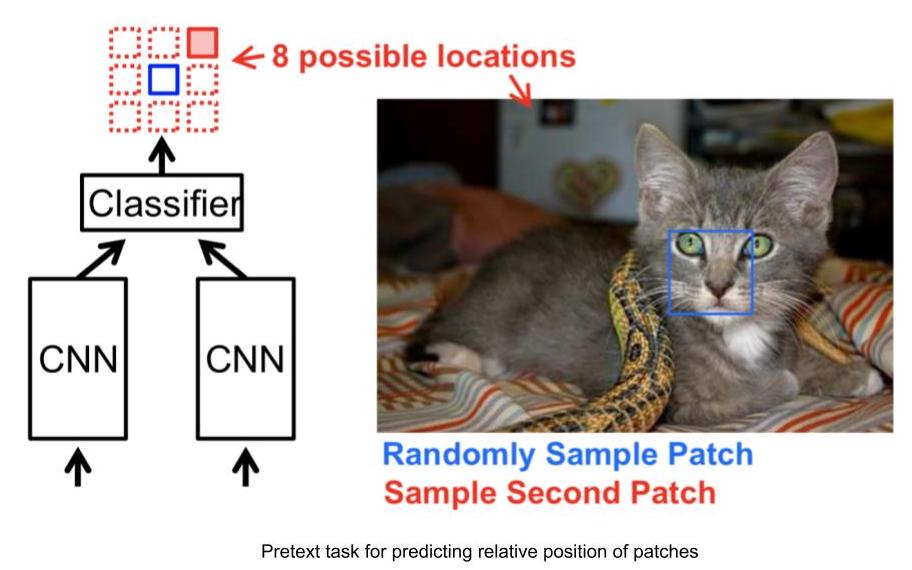
图 3: 相对位置任务

通过相对位置预测任务来学习的视觉性「表示」

我们可以用近邻法，用网路对图像中一个格生成的基础特征「表示」中的来评估学习视觉性「表示」的有效度。

• 比较下数据集中所有图片的CNN特征，那将会用来检索的样本池。
• 对图片中一个格计算所有CNN特征
• 在可用图像的特征向量池中，辨认所需图像的特征向量的近邻，

相对位置任务找出与输入图像非常相似的格(图片中一个格型部份)，找出同时保持一些因素，比如物体颜色。所以，其相对位置任务是能够学到视觉性表示，那个图片格中的一些表示和别的表示视觉上相似的话，那它们就是空间性上相近。

图 4: 相对位置: 近邻版

预测旋转的图片

• 预测旋转了是最受欢迎的前置任务之一，也就有一个简单和直接的架构和只要求简单的样本。
• 我们旋转图片0或90﹑180﹑270度，然后输入这些图片到网路中来预测图片旋转了多少，然后网路进行4种不同的预测来预测旋转了多少。
• 预测旋转不会生成任何语义分割的感觉，我们会使用这个前置任务如代理一样来学一些特征和表示，然后用这些特征和表示在后期工作。

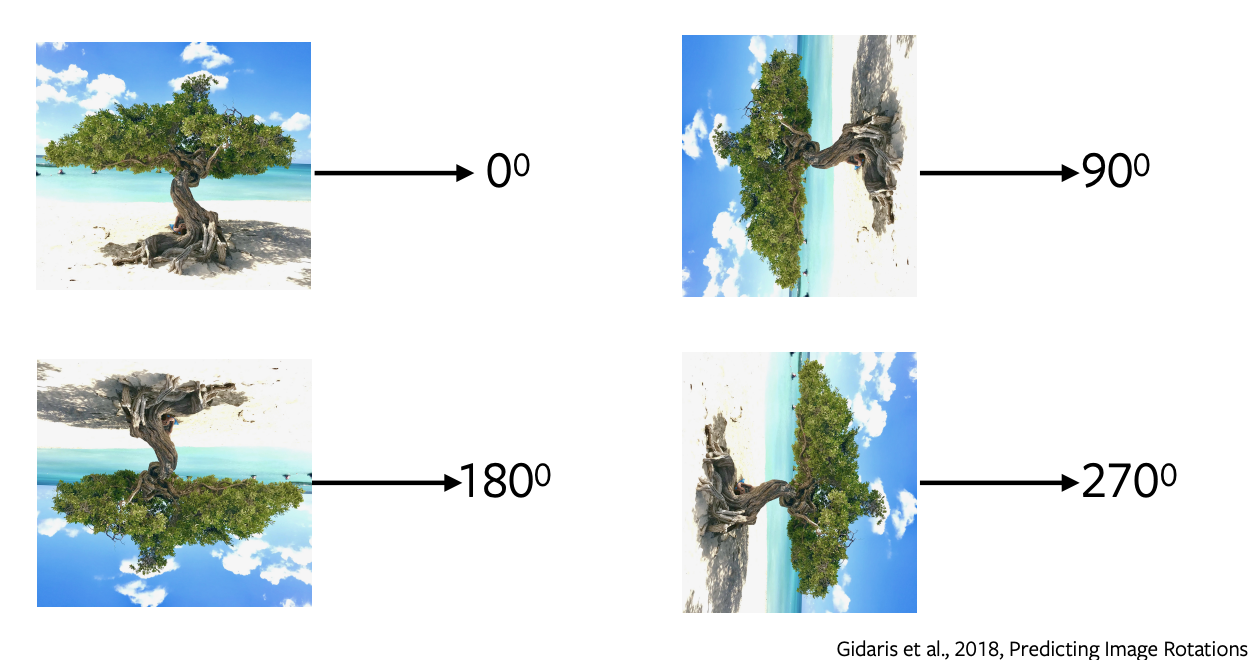
图 5: 旋转了的图像

为什么旋转了的图像能行或有帮助?

它一直以来都凭经验地证明出能行的。它背后的能行的解释就是为了预测旋转了多少，模型就要明白界限和图片的表示，比如，它将会把天空分离开水或沙，或它将会明白树木会向上生长。

彩色化

图 6: 彩色化

在这个前置任务，我们对灰图进行预测其本身的颜色。它可以是其他图片制订了一些东西后的版本，我们移除颜色，然后输入这个灰图到网路中去预测其颜色。这个工作就如把一些灰色电影进行彩色化 [//]: <>(我们可以用这个前置任务)。背后的能行的解释就是网路要明白一些有用的信息，比如树木是绿色的，天空是蓝色的，然后就这样，那样的。

非常重要的是要明白彩图化不是确定性的，数个可能正确的解决方法同时存在。所以如果物体是有数个可能的颜色，那网路就会把它灰色化，也就是多个可能的解决方法的平均值。最近有些做法就是用可变自动编码器和用潜在变量来实行多种不一样的彩图化。

填空任务

我们隐藏图片中一些部分，然后用可见的部份来预测隐藏的部分。这能行是因为网路会学到数据含隐的结构，就如表示路上的行走的车，建筑物是由窗和门和别的东西组合起来的。

用在视频的前置任务

视频是由很多帧组合起来，然后这个概念就是自我监督背后的想法，也就是这可以用来在一些前置任务，比如很视频中的帧的顺序﹑填空任务﹑追踪目标。

「順序打亂後學習式」

图 7: 插补

给一些帧，然后我们抽当中三个帧，如果它们是顺序的，那就是正，相反如果不是顺序的，那就是负。现在这个就变成二元分类问题去预测那些帧是顺序或不是的。然后，就给一个起点和终点，我们检查中间那一帧是不是前一帧和后一帧在一起的话是不是顺序的。

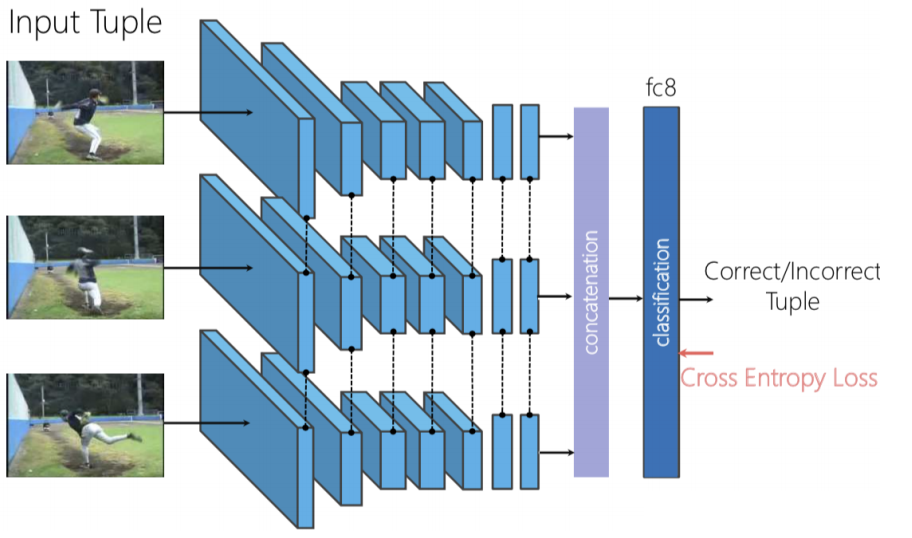
图 8: 「順序打亂後學習式」的架构

我们可以用三合式连体网络，也就是三个帧是独立地输入到向前式网路和我们把生成的特征连接起来，然后就来个二进制分类，以预测这些帧是否被顺序的。

图 9: 近邻式表示

再说多次，我们可以用近邻演算法来看出我们的网路是学到了什么。在上方的图9，我们先有一个查询帧来输入到前馈网路中取得特征表示和之后去看表示的空间中的近邻(各像数附近的像素)。当以，我们以ImageNet和「順序打亂後學習式」﹑随机性来进行比较时，各像数附近的像素中就看到明显的差异。

ImageNet优良于把整个图片中的所有内容合并起来，就如它在第一个输入询问中能想出这个是体育馆环境。相似的，它能以环境中有草来想出这是户外。在第二个输入询问中，我们可以看到随机性。我们可以看到它对背景颜色所有的重视性。

观察一下「顺序打乱后学习式」，也不能立即清楚它是否注意在颜色上或内容上。经过进一步检查并观察了各种示例后，就看出它注意在人物的姿势上。比如，无视场景或背景色的话，在第一张图中人物是上下翻转的，而第二张的脚的位置就特别地相似其输入查询的帧。原因是背后所有东西，前置任务是预测那些帧们是不是顺序，而做出这些东西的话，网路要注意什么物体是移动的，在这里的话，比如是人。

已证明了数量性的微调「表示」到人类关键点估測任务，就如给人类一张图，然后去估出那些关键点，如鼻子或左肩﹑右肩﹑左肘﹑右肘等。这些方法就在追踪姿势估测中十分有用。

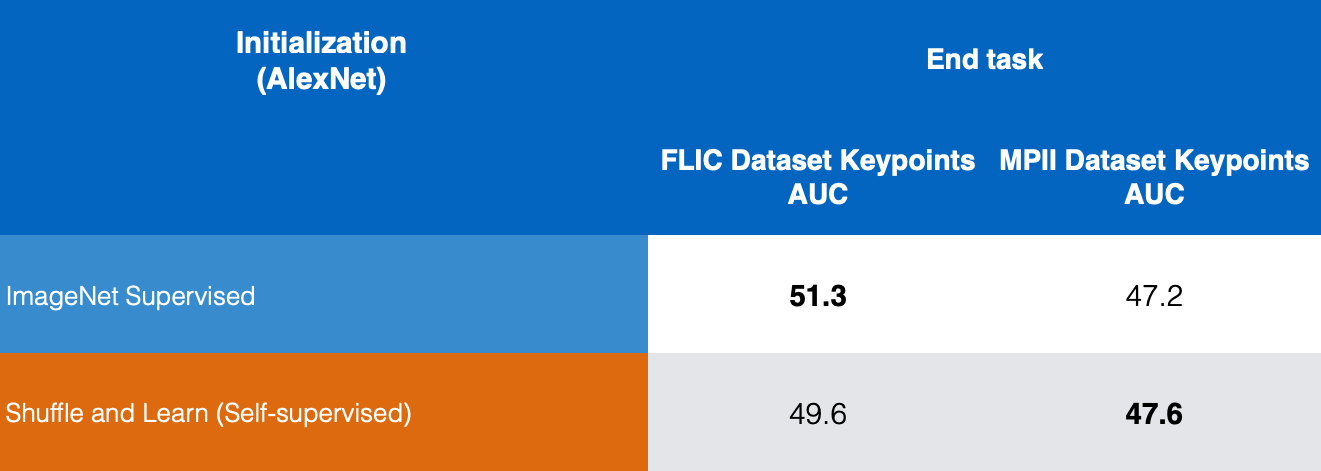
图 10: 关键点估测

在图10中，我们在FLIC和MPII数据集中比较监督版的ImageNet和自我监督版的「顺序打乱后学习式」，和我们看到「顺序打乱后学习式」在关键点估测中给出好成绩。

视频和声音的前置任务

视频和声音是多种式模型，也就是我们有两种形式和两种感知输入，一个是给视频，而另一个是给声音。而我们尝试去预测给予的一部份音轨和另一部份视频是否对应。

图 11: 视频和声音采样 给予有鼓声的视频，取一些视频帧和其对应的音轨，那就叫这个为正集合。下一步，取一些鼓声视频的音轨和吉他视频的帧，然后叫这个为负集合。现在我们训练这个网路去解决这个二进制分类问题。
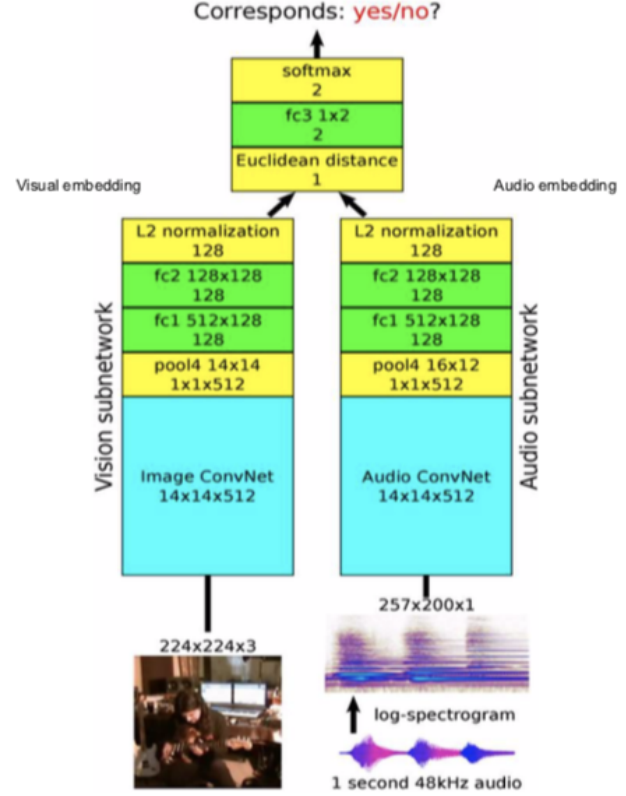
图 12: 架构 **架构:** 输入一些视频帧到视觉网路中，然后就输入一些音讯到音讯网路中，那就给128维特征和嵌入(embeddings)，然后我们将它们融合在一起去解开这个二进制分类问题，也就是这些视频帧和音讯是不是对应的。 它也可以被用来预测在一个视频帧中的发声物。背后的原理是如果它是吉他声，网路就大致要明白吉他的外观，然后对于鼓来说也应该如此。 ## [明白"前置”任务的学习了的内容](https://www.youtube.com/watch?v=0KeR6i1_56g&t=2426s) * 前置任务应该是**附加的** * 用「相对位置」和「色彩化」的前置任务来说。我们可以用训练一个模型去学两个前置任务来提高性能，如以下所示:
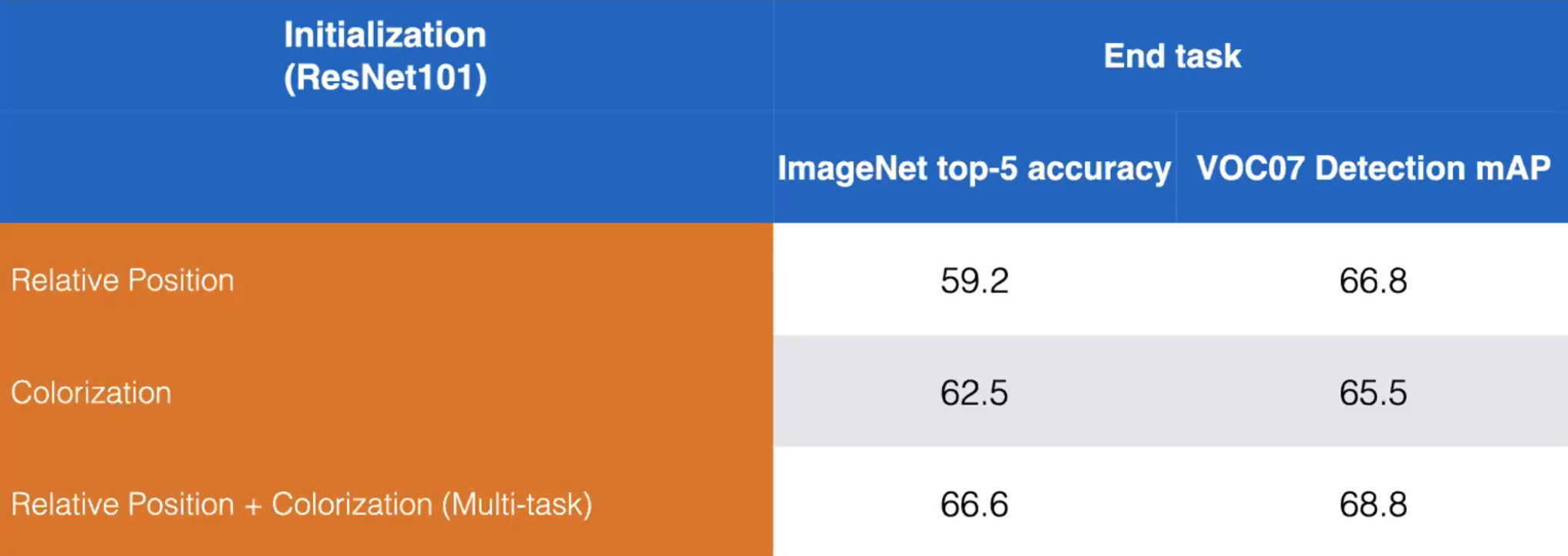
图 13: 相对位置和彩色化的前置任务的同时使用和不同时使用在训练上的比较。 ResNet101 (Misra) * 一个单一的前置任务或许对学习SS中的「表示 」来说不是正确答案 * 对于不同的(很困难的)预测任务来说，它们的前置任务可以是差别很大。 * 前置任务之一的相对位置是很简单的，因为它只是一个简单的分类。 * 覆盖然后填补就十分之难了--> **更好的表示** * **对比法**就比前置任务能生成更多的资料 * **问题:** 如何才能训练多个前置任务呢? * 前置任务的输出是根据于其输出。网络最后一个全连接层可以根据它的批次类型(batch type)来**换掉**。 * 比如例子是一个黑和白的图片是被输入到一个能生成彩色图片的网路中。之后，最后的那一层就被换掉了，之后就给一些批次(batch)去预测相对的位置。 * **问题:** 我们要训练多少前置任务呢? * 经验法则:有一个十分难的前置任务，它能提升后期任务。 * 在实践中，前置任务是被训练过的，同时是不能重新训练。在开发期间，它是整个流程的一部份。 ## 在自我监督学习上做大起来 ### 拼图(Jigsaw Puzzles) * 把图片切成多个部份，如拼图一样，然后打乱这些拼图。而模型的任务就是去把这些拼图拼回原本的图片。 (Noorozi & Favaro, 2016) * 预测那些交换拼图的移动是对输入图片用过的 * 这是以生成拼图批次(batches of tiles)，**也就是独立评估每一个图片中的拼图。** 所有的卷积输出之后就一起被连起来，然后就用这个连起来的来预测拼图有那一种交换移动，请看如下图了解
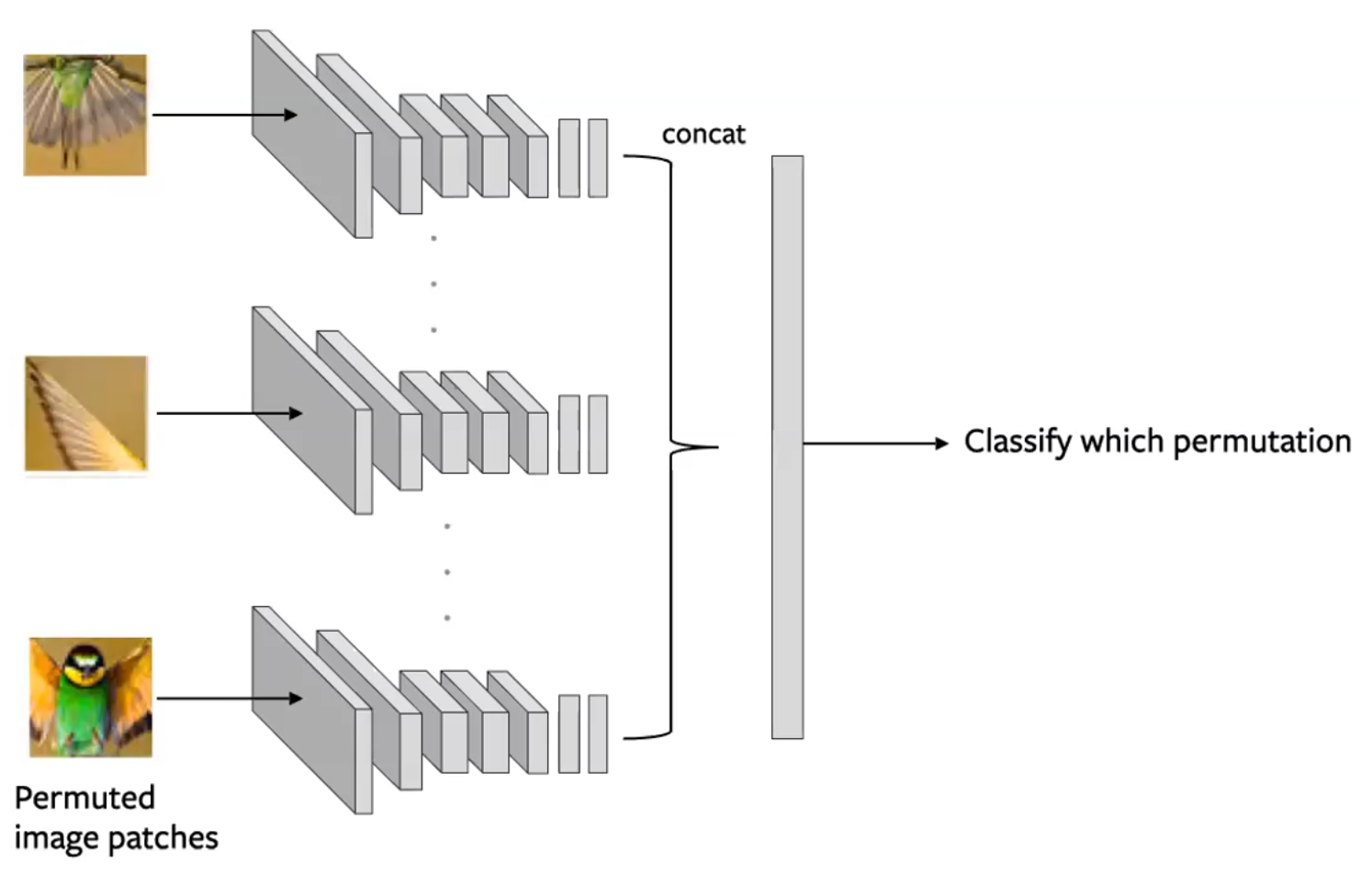
图 14: 用在拼图式前置任务的连体网络架构。每一个拼图都是独立地输入的，之后就以编码方式连起来来预测拼动有那一种交换移动。 (Misra) * 注意事项: 1. 用一个交换移动的集合(也就是从9!开始，使用100) 2. N方式卷积网就用共享参数 3. 问题的复杂度是集合的大小。就是*你要预测的资料的大小。* * 有时，这个方法能执行在后期工作，而且比监督方法好，因为网路能学到一些有关输入本身的几何形状概念。 * 小样本学习: 訓用的例子数量有限 * **自我监督表示不是真的那么提高样品效率** ### 评估：*比较一下* 微调和线性分类器 这种评估形式是一种**转移学习**。 * **微调**:当用在后期工作中用上了，我们使用整个网络就如**初始化**那样，也就用它来训练一个新的，更新所有权重。 * **线性分类器**: 在前置任务旁，我们训练一个细的线性分类器去执行后期任务，让整个网路保持完整。 > 好的「表示」应该只用了**小小的训练**来转移。 * 在**众多不同的任务**上评估前置任务是有帮助性的，也就是我们可以这样做，用网路中每一层来生成和提取出各个「表示」，然后当作**固定的特征**来用，然后评估这些表示它们的可用性。 * 测量:平均精度均值(Mean Average Precision ，简称mAP)精确度是在所有不同我们考虑到的工作中被平均起来。 * 有些这些任务的例子中包括:物体识别(使用微调)，表面法线估计(Surface Normal Estimation)(请看NYU-v2数据集) * 到底每一层学到什么呢? * 一般来说，每层会变得更深，使用每层的「表示」的话，平均精度均值会在后期工作中上升。 * 相反，**最后的那一层**就会在平均精度均值mAP中有一个急剧下降，那是因为那一层就会变得**很专修**一些东西。 * 这与受监督的网络的意义相反，因为mAP通常总是随层深度的增加而上升。 * 这显示出初期任务不是和后期工作**不是一致**