对抗性生成网络GANs

对抗性生成网络(GANs)

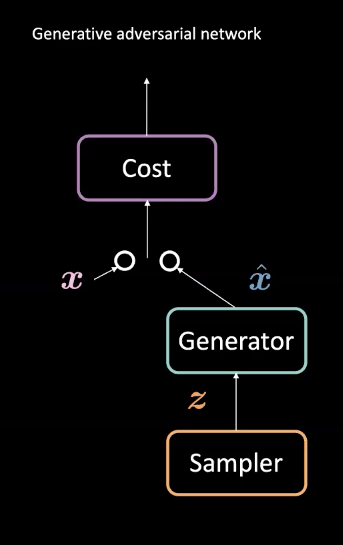
图1:GAN结构

GANs 是一种用在无监督机器学习的神经网路。它们包含两个对抗模块:生成器_和_代价网络。它们都互相竞争，_代价网络_去掉冒牌货，而同时_生成器_就尝试生成接近真实的冒牌货来骗这个辨别器$\vect{\hat{x}}$。在这种互相竞争后，模型就学习到一个能生成十分真实的冒牌货的生成器。它们能用在一些任务，比如预测未来或在训练特定数据集后生成图片。

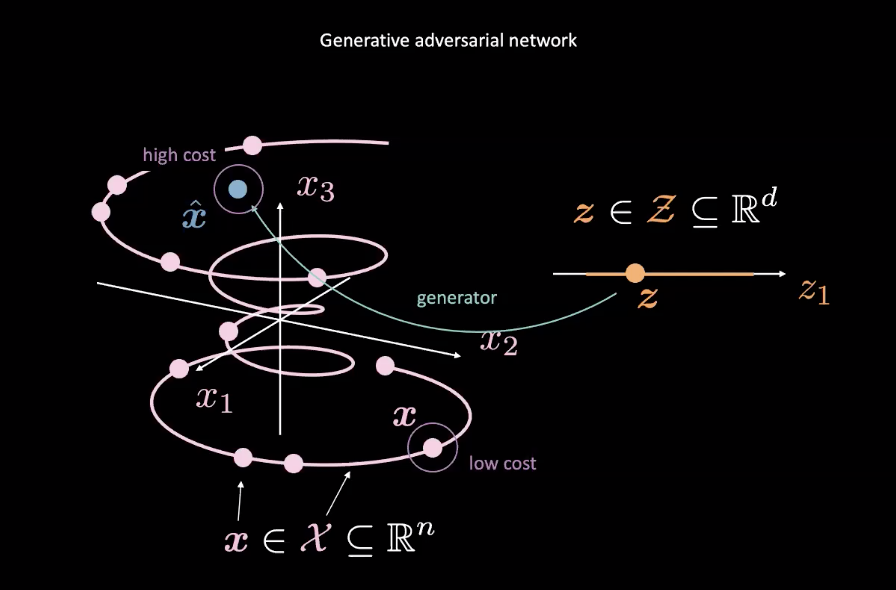
图2: 由随机变量绘制出GANs

众多GANs多是是能量基础模型 (EBMs)的例子。比如这样，代价网络是被训练对接近真实的数据分布的输入只输出低代价，真实的数据就是上方图2的粉$\vect{x}$。数据来自其他分布，比如图2中的蓝$\vect{\hat{x}}$，这些分布应该有高代价。一个均方误差损失(mean squared error loss 或MSE loss)是一般都被用来计算代价网络的性能。值得注意的是代价函数输出一个正标量数,而这个正标量数是在指定范围之内(比如: $\text{代价} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$)。这是十分不像传统判别器那样，它用离散的分类器来分类它的输入。

同时，生成器网路($\text{生成器} : \mathcal{Z} \rightarrow \mathbb{R}^n$)是被训练成会改善它的摆布随机变量$\vect{z}$的能力，就是為了生成更真实的数据x-head來骗代价网路。而生成器就是根据代价网的输出来训练，而且生成器也會最小化$\vect{\hat{x}}$的能量。我们表示这是「能量」如以下写法$C(G(\vect{z}))$，那个$C(\cdot)$是代价网路同时$G(\cdot)$是生成器网路。

训练代价网路是根基于降低均方误差损失(mean squared error loss 或MSE loss)，同时训练生成器网路是由降低代价网路，使用$C(\vect{\hat{x}})$梯度($\vect{\hat{x}}$)相对$\vect{\hat{x}}$。

为了确保流形数据之外的点有高代价和流形数据之内的点有低代价，代价网络的损失函数$\mathcal{L}_{C}$是 $C(x)+[m-C(G(\vect{z}))]^+$，而$m$是有一个代表边界的边界正数。 降低$\mathcal{L}_{C}$要求$C(\vect{x}) \rightarrow 0$而且$C(G(\vect{z})) \rightarrow m$。而生成器的损失部份$\mathcal{L}_{G}$简单的只是$C(G(\vect{z}))$，这是为了令生成器确保$C(G(\vect{z})) \rightarrow 0$。相反地，这样是会制造出不稳定，就是这样的話这样$0 \leftarrow C(G(\vect{z})) \rightarrow m$

可变自动编码器(VAE)與对抗性生成网络(GANs)的差別

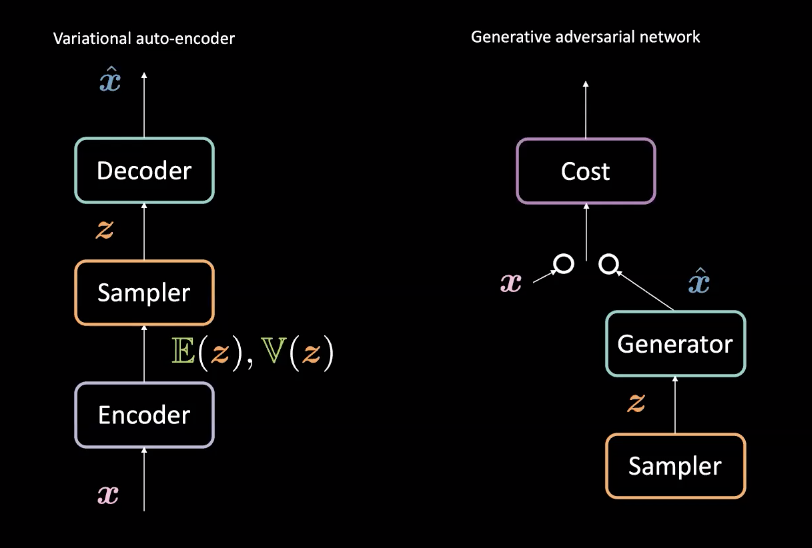
图3: 可变自动编码器 (左) vs. 对抗性生成网络 (右) - 他们的结构

拿第8周的可变自动编码器（VAEs）比较下，对抗性生成网络GANs所有的生成器是跟可变自动编码器有点不一样。回想下，VAEs用_编码器_来映射「输入$\vect{x}$」到潜在空间$\mathcal{Z}$，而之后又用_解码器_由潜在空间$\mathcal{Z}$到数据空间来得到$\vect{\hat{x}}$。之后它用「重建损失」来推$\vect{x}$的位置来令$\vect{x}$和$\vect{\hat{x}}$变得更像。 对抗性生成网络(GANs)，就不一样地，在一个互相对抗的环境下训练，就如上方说的有着一个生成器和代价网路互相对抗着。这些网路是依次序性地由反向传播和由基于梯度的方法来训练。

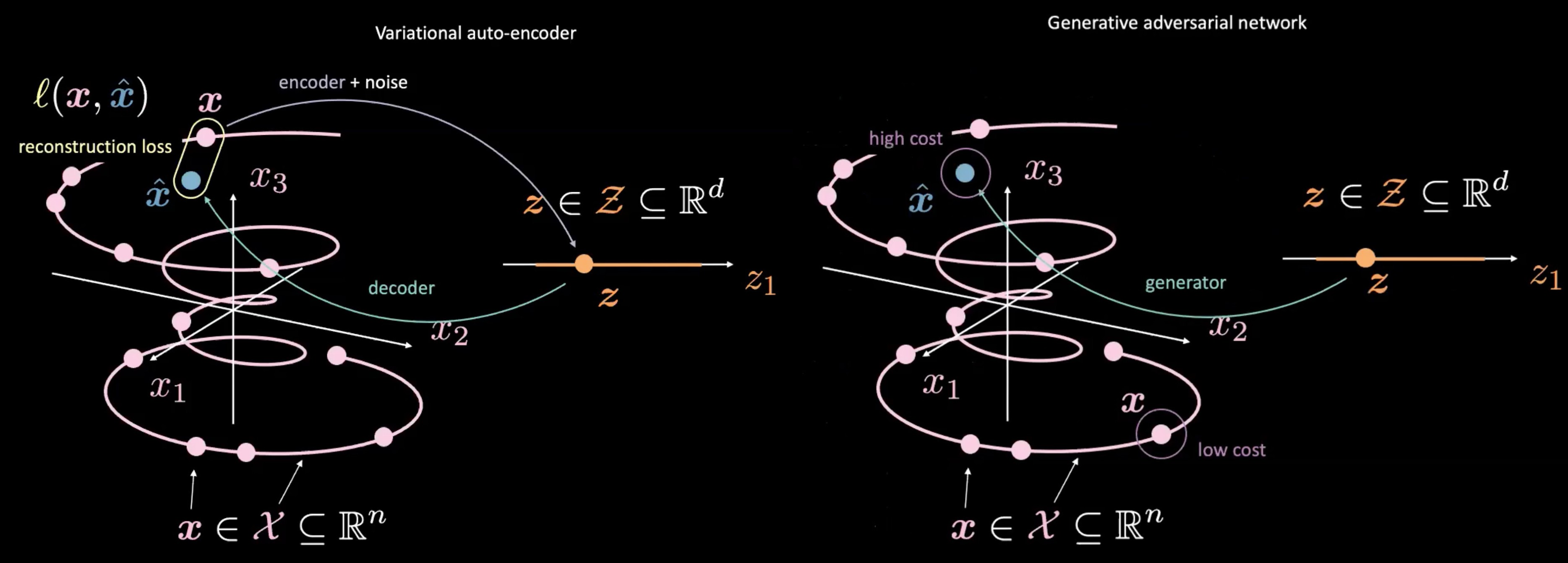
图4: 可变自动编码器 (左) vs. 对抗性生成网络 (右) - 由随机样品$\vect{z}$映射过去。

对抗性生成网络(GANs)是和可变自动编码器(VAEs)有点不一样,就是在于它们如果生产和使用$\vect{z}$。 对抗性生成网络(GANs)开始是用样品$\vect{z}$，有如可变自动编码器(VAE)的潜在空间。它们之后用生成网路去映射$\vect{z}$到$\vect{\hat{x}}$。这个$\vect{\hat{x}}$是之后送到判别器或代价网路来评估它的”真实度”。其中可变自动编码器(VAE)和 对抗性生成网络(GAN)的一个主要分别是…就是我们不用去测量生成器的输出$\vect{\hat{x}}$和真实数据$\vect{x}$的直接关系(比如重建损失)。反而，我们去训练生成器去生成$\vect{\hat{x}}$就是追求$\vect{\hat{x}}$d和$\vect{x}$要变得相似，就是这样，那辨别器/代价网络才生成一个分数是十分接近真实的数据X，或更”真实” 。

用对抗性生成网络(GANs)时，最有可能令人做错的地方

的确抗性生成网络(GANs)在制作生成器数据时是十分强大的，但都有很多容易令人做错的地方。

1. 制作

就如生成器会随着训练而改进，判别器性能就会变差，因为判别器不能去容易地说出真数据和假数据的分别。如果生成器是完美的话，那「真数据的流形」和「假数据的流形」就会完全地在一起，同时判别器就会出现很多错误分类。

这就提出了GAN「收敛」时出现的问题:辨别器的反馈就随时间变得无意义。如果GAN一直地去训练，更训练到变成给随机反馈，那生成器就会开始用这些垃圾没用的反馈来训练，最后连生成器的的质量都完全下降。 请参阅GAN中的训练「收敛」]

所以结果是这种生成器和辨别器之间的对抗性质的话，那就是一个不稳定的平衡点，而不是稳定点。

2. 消失的梯度

比如我们在GAN中用的是二元交叉熵损失:

当辨别器的辨别能力变得更好时，那$D(\vect{x})$就会接近$1$，而$D(\vect{\hat{x}})$就会接近$0$。这个变得更好时就会令输出走到代价网路的平坦地区，那里的梯度是更饱和的。这些平坦地区提供细小和消失的梯度，同时会阻碍生成器的训练。所以当训练GAN时，你会肯定清楚当辨别能力变得更好时，代价也同时会逐渐上升。

3. 崩溃模式

当生成器把所有$\vect{z}$由样品映射到一个$\vect{\hat{x}}$去骗辨别器时，那生成器就只会生成那一个 $\vect{\hat{x}}$。最终地，那个辨别器就会去学来特别地检测这那一个假输入。结果是，生成器会简单的找出下一个最合理的$\vect{\hat{x}}$，然后这个循环不停的循环下去。结果的是，辨别器在多个假$\vect{\hat{x}}$的循环中困在局部最小值(local-minima)。最有可能的解决方法是對生成器实行一些惩罚，那就是当有不同的输入给生成器时，而它却生成同一样的输出的话，那就给予相应惩罚。

深度卷积对抗性生成网络(简称DCGAN)源代码

以下例子的源代码可以在 [这里找到]。(https://github.com/pytorch/examples/blob/master/dcgan/main.py).

生成器

以下例子的源代码可以在这里找到。 生成器

1. 生成器使用数个模组来对输入进行「升采样」，每个模组是多个nn.ConvTranspose2d，然后是nn.BatchNorm2d和 nn.ReLU。
2. 在顺序函数(nn.Sequential)的最后部份，网路使用nn.Tanh()去压缩后方的输出到(-1,1)。
3. 而用来输入的随机向量的大小为$nz$。而输出的大小为$nc \times 64 \times 64$，那个$nc$是频道数量。

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            #输入Z被输入到卷积层
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # 现在大小为: (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # 现在大小为: (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # 现在大小为: (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # 现在大小为: (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # 现在大小为: (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

辨别器

1. 使用nn.LeakyReLU来作为激活函数是十分重要的，因为防止当在负区域时出现梯度消失。没有了这些梯度的话，生成器是不会得到任何更新。
2. 在顺序函数(nn.Sequential)的最后部份，辨别器使用nn.Sigmoid()来辨别输入。

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            #nc是频道数量
            # 输入大小是 (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # 现在大小为: (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # 现在大小为: (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # 现在大小为:(ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # 现在大小为:(ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

上方兩個类初始化为netG 和 netD。

对抗性生成网络(GAN)的损失函数

我们用二进制交叉熵（BCE）来对应输出和目标。

criterion = nn.BCELoss()

设定

我们设定fixed_noise的大小为opt.batchSize的和随机向量的长度nz。我们也给真实的数据和生成了的数据(假的)各自创造标签为真标签(real_label) 和 假标签(fake_label)。

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

然后我们给判别器网路和生成器网路设定各自的优化器。

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

训练

训练中的每一个阶段(epoch)都分为两个步骤。

第一步是更新辨别器网路。这是分开两部份来完成。第一部，我们给予辨别器一些来自dataloaders的真数据来计算输出和real_label之间的损失，之后就反向传播来累积梯度。第二步，那就是我们给辨别器一些生成器网路用fixed_noise生成的数据来计算输出和fake_label之间的损失，之后就反向传播来累积梯度。最后，我们使用累积得来的梯度来给辨别器网路更新参数。

注意到的一点是我们要分离(detach)假数据来防止当训练辨别器时梯度会传播到生成器。

而且我们也看到只要在开头的地方使用一次zero_grad()去清理梯度，就能令来自真数据和假数据的梯度来更新我们想更新的东西。那里使用了两个.backward()是来积累这些梯度。最后我们只需要使用一次optimizerD.step()来更新参数。

# train with real
# 用真实的数据来训练
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# train with fake
# 用假的数据来训练
noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

第二步就是更新生成器网路。这次，我们给辨别器假数据，但是用真标签来计算损失!目的是为了训练生成器生成更真实的$\vect{\hat{x}}$。

netG.zero_grad()
label.fill_(real_label)  # fake labels are real for generator cost
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()