世界模型（World Model）和生成对抗网络（Generative Adversarial Networks）

自主控制世界模型

自监督学习的一个重要用处是用来学习世界模型。当人们做事情时，我们有着一个内在模型来模拟世界是怎麽运作的，譬如当我们9个月大的时候，我们能够通过观察外界来培养物理概念的直觉思维，在某种意义上来说这和自监督学习非常相似。正如自监督模型学习隐变量的过程一样，我们通过学习如何预测将会发生的事情来学习抽象概念。进一步来说，我们的内在模型让我们能对外界有所反应。比如说，当我们学到了物理直觉和怎样控制手后，我们可以用这些学会的东西来预测和进行“抓住一支正在往下掉的笔”这一行为。

什麽是“世界模型”？

自动化智能系统是由四个主要模组组成的（图1）。第一个模组是用来观察和计算世界表征的感知模组。这通过观察而计算出来的世界表征其实并不完整，这是因为1）主体并不能观察到整个宇宙；2）观察到的也并不一定准确。有一点要注意的是，在前馈模型中感知模组只存在于第一个时间步中。第二个模组是基于观察到的表征来计算有可能的下一步的演员模组（也叫策略模组）。第三个模组是模型模组。当给定世界表征（有时候还有隐变量）后，这模组可以用来预测下一步行动后世界表征将会变成怎么样。这预测会被传到下一个时间步来当作下一个世界表征。正因如此，在最开始的时间步后，模型模组就代替了感知模组来计算世界表征。图2详细地描述了这前馈过程。第四个模组是计算行动所会带来的代价的评判家模组。譬如说，当给定了笔往下掉的速度后，如果一个人以某种方式来移动他的手，那他有多大可能性会抓不住这往下掉的笔。

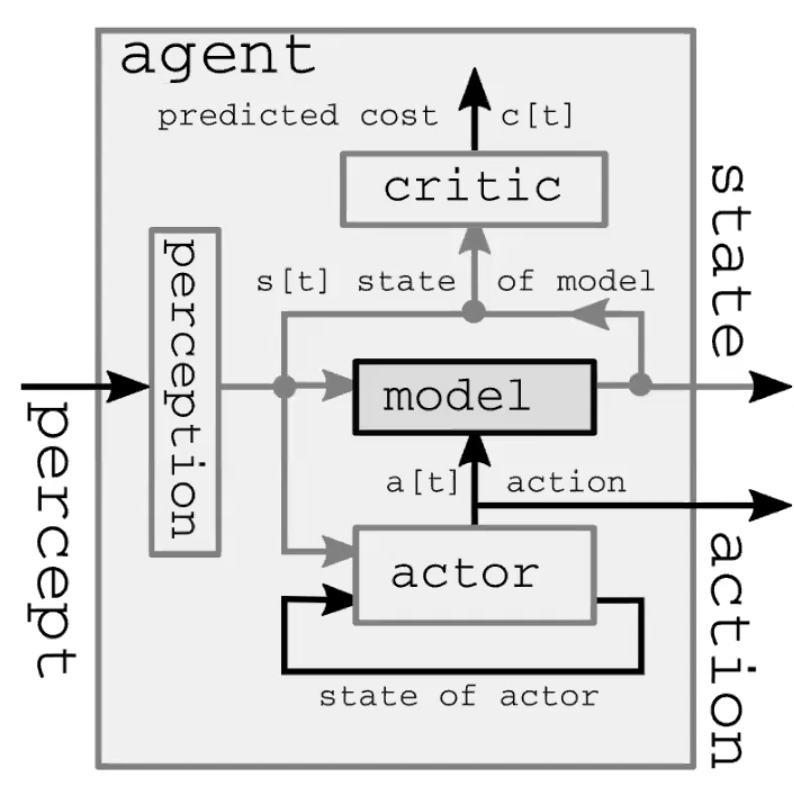
图1: 自动化智能系统的世界模型结构详解。

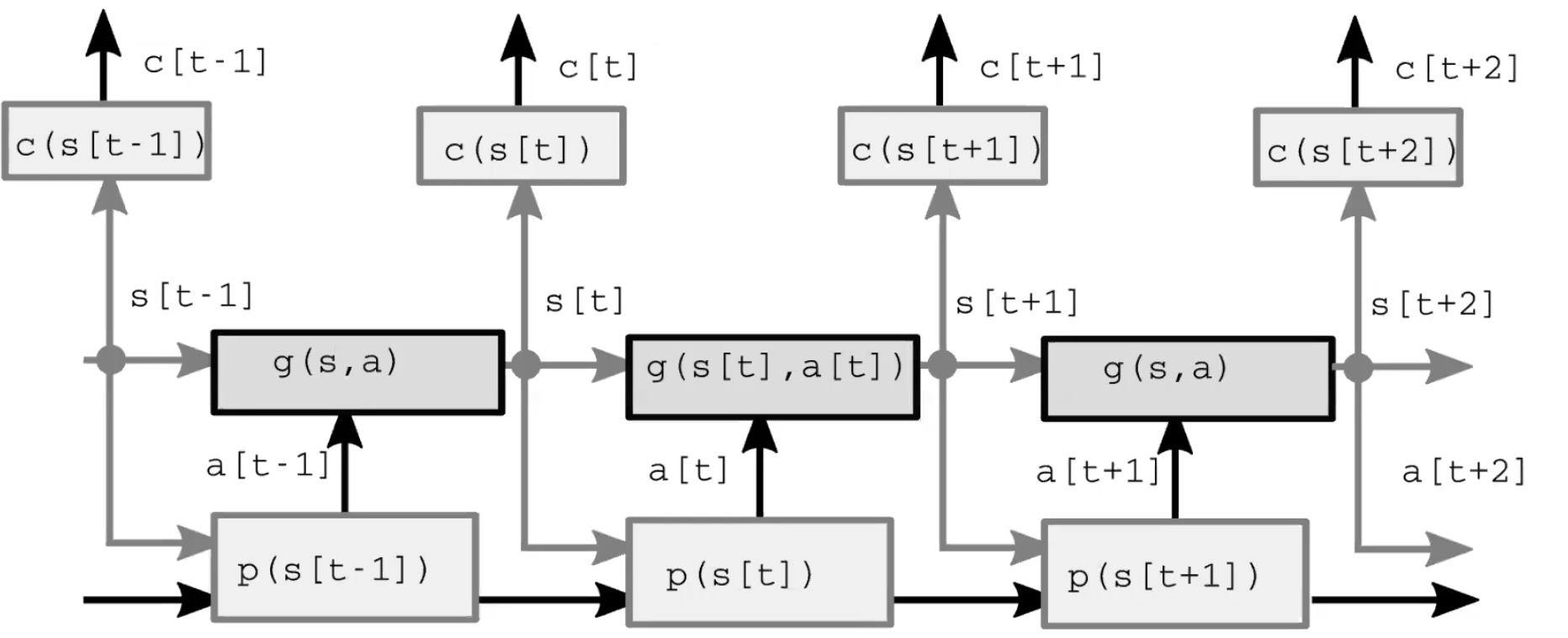
图2: 模型结构。

经典设定

在经典的最优控制中，演员模组（策略模组）并不存在，取而代之的是一个行动变量。用来优化最优控制的方法叫作模型预测控制，在1960年代当NASA从人手计算（主要是黑人女数学家）切换到计算机后，就曾用模型预测控制来计算火箭轨迹。我们可以把这种系统看作是没展开的RNN，把行动变量看作是隐变量，并用反向传播算法和梯度下降算法（也可以用其他的方法例如离散行动集动态规划）来推断哪一序列行动能将每一时间步的代价的总和降到最低。

虽然优化隐变量和优化参数的过程类似，但我们用“推断”来形容隐变量优化而用“学习”来形容参数优化。一个很重要的区别是隐变量因选样而异，但参数是被所有选样共享的。

改善

因为我们不想每次规划时都要计算很复杂的反向传播，所以我们用和变分自编码器一样的方法来改善稀疏编码：训练一个编码器来从世界表征直接预测最优行动序列。在这情况下，这编码器一般被叫作策略网络。

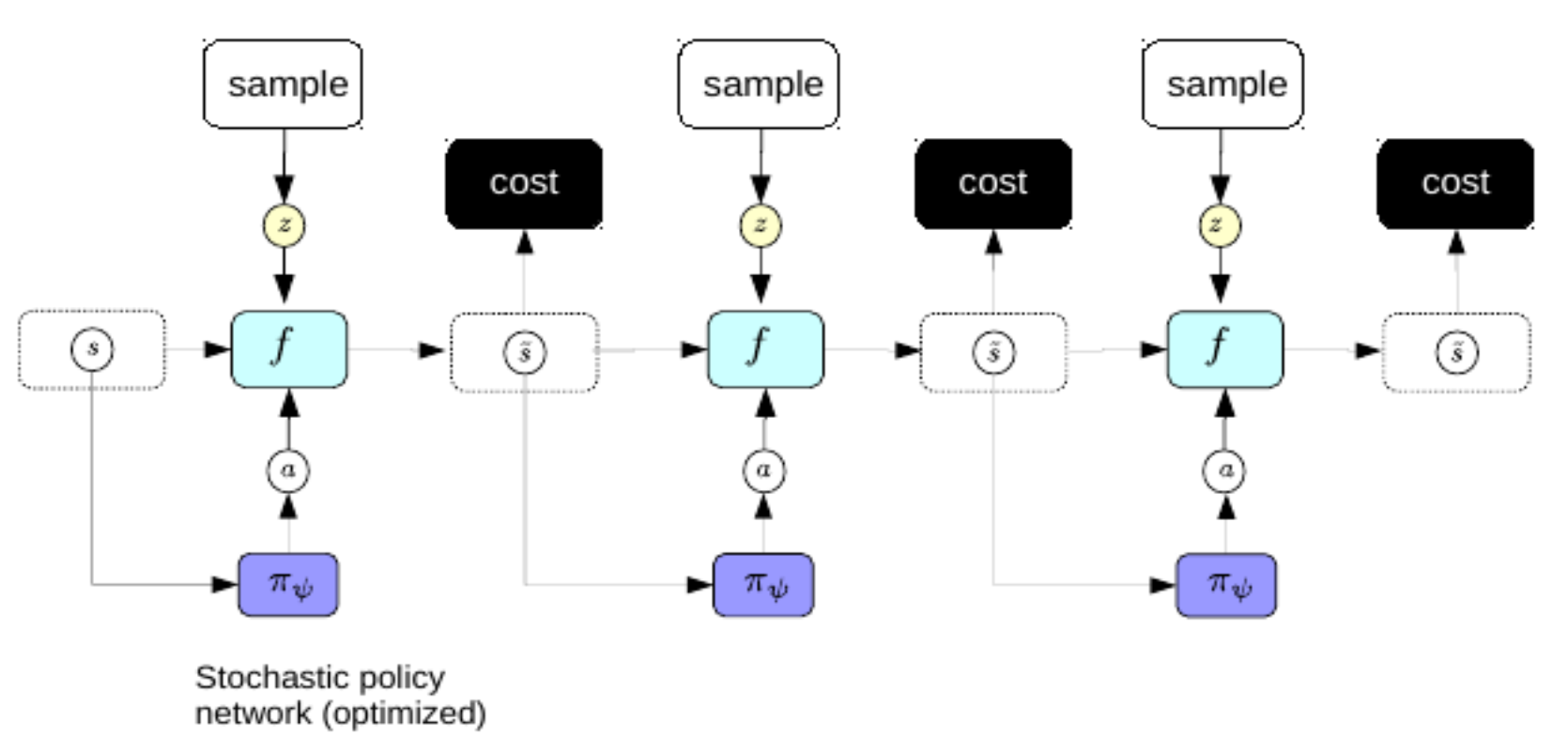
图3: 策略网络。

当我们成功训练好一个策略网络后，一旦有了世界表征，我们可以用它和这策略网络来马上预测最优行动序列。

强化学习

强化学习和我们目前学到内容的最大的区别有两点：

1. 在强化学习环境中，代价函数其实是个黑盒子。换句话说，强化学习的主体根本不懂什么是奖励的本质。
2. 在强化学习中，我们不用前向模型来推进环境。相反，我们和真实环境互动来观察到底发生了什么。虽然在真实环境中，因为我们对环境的测量并不完美，所以并不是每次都能够预测到将会发生什么。

强化学习最主要的问题在于代价函数并不是可微的，这意味着我们只能通过反复试验来学习。然而这样的话问题就变成了怎么样才能更有效率地探索整个环境。就算解决了这问题后，我们还会面临另一个根本问题：到底要探索还是开发。我们是要采取探索整个环境的行动呢，还是利用已经学到的东西来尽可能获取高奖励？

强化学习中一个很受欢迎的算法家族叫作演员-评判家算法，此算法要求同时训练一个演员和一个评判家。很多其他的强化学习算法在训练模型的代价函数（评判家）这一点上也跟这算法类似。在演员-评判家算法中，评判家的作用是学习价值函数的期望值。因为评判家仅仅是一个普通的神经网络，我们可以用反向传播来优化它。总的来说，演员负责提出当前应该执行的行动，而评判家则负责预测代价函数。相比只有演员没有评判家的强化学习算法，演员和评判家共同合作能够让学习更加有效率。要注意的是，如果没有一个好的世界模型，学习会变得更加困难，譬如说，停在悬崖上的车并不知道掉下悬崖是个坏主意。正因为人类和动物在脑中都有着好的世界模型，人类和动物才能够比强化学习主体更加有效率地学习。

因为内在随机性（偶然性和认知不确定性）的存在，我们并不是能每次都准确地预测未来会发生什么。偶然性是由我们不能控制或者观察到的事情所导致的。而认知不确定性则是由因不够训练数据而无法预测未来所导致的。

我们希望前向模型能够预测

在这$z$是个我们不知道具体值的隐变量。$z$代表那些世界中我们不知道但仍能影响预测的东西（偶然性）。我们可以用稀疏性，噪声或编码器来正規化$z$。我们也可以用前向模型来学习怎样规划。这系统中的解码器是用来解码状态表征和不确定性$z$的合并。在最好情况下，$z$可以最小化$\hat s_{t+1}$和实际观察到的$s_{t+1}$之间的差别。

生成对抗网络 (GAN)

GAN有很多变种，而在这里我们把GAN看作是一种用对比学习方法的能量模型。GAN将对比选样的能量往上升的同时把训练选样的能量往下降。一个基本的GAN是由两个神经网略部分组成的：一个能智能地生成对比选样的生成器和一个判别器（有时候也叫评判家）。基本上来说这判别器就是一个当作能量模型的代价函数。

GAN的输入有两种：训练选样和对比选样。训练选样会被输入到判别器，然后这些训练选样的能量会下降，而对比选样则是通过隐变量成生的。GAN会先从特定的分布中抽样获得隐变量，然后把隐变量输入到生成器中，让生成器生成和训练选样类似的对比选样，最后把这些对比选样输入到判别器中让它们的能量往上升。判别器的损失函数是这样子的：

在这里$L_d$可以是$F(y) + [m - F(\bar{y})]^+$ or $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$这样的间隔损失函数，只要这损失函数能让$F(y)$下降的同时让$F(\bar{y})$上升就行。在这种情况下，$y$是标签，而$bar{y}$则是除了$y$以外最低能量的反应变量。 生成器的损失函数和判别器的不一样：

在这里$z$是隐变量而$G$是生成器神经网络。我们想要让生成器调整其权重进而生成可以骗到判别器的低能量$\bar{y}$。

这种模型之所以叫生成对抗网络的原因是因为我们有两个互相对抗的目标函数，而且我们还要同时优化这两个目标函数。我们的目标是找到这两个函数的纳什均衡。因此，其实这并不是一个梯度下降问题，因为梯度下降并不能做到这一点。

如果选样太接近于真实的流形的话，我们就会面临一些问题了。假设我们有一个无限薄的流形，判别器需要在这流形外获得$0$的可能性的同时在流形上获得无限大的可能性。因为这很难实现，GAN用Sigmoid函数来在流形外获得$0$的可能性并在流形上获得$1$的可能性。如果我们的模型训练好之后能够完全做到这点的话，那这模型就根本没用了。能量函数会变得非常不光滑，所有数据流形外的能量会变成无限大，而所有数据流形上的能量会变$0$。我们不想让能量在很短距离内马上从$0$变成无限大。不少学者提出了各种正则化能量函数的方法来解决这问题，譬如基于GAN的Wasserstein GAN就是一个很好的例子，它通过限制判别器权重大小的方法来尝试解决这一问题。