判别类循环稀疏自编码器 (Discriminative Recurrent Sparse Auto-Encoder) and 组稀疏 (Group Sparsity)

判别类循环稀疏自编码器 (DrSAE)

DrSAE的设计结合了稀疏编码（稀疏自编码器）和判别类训练。

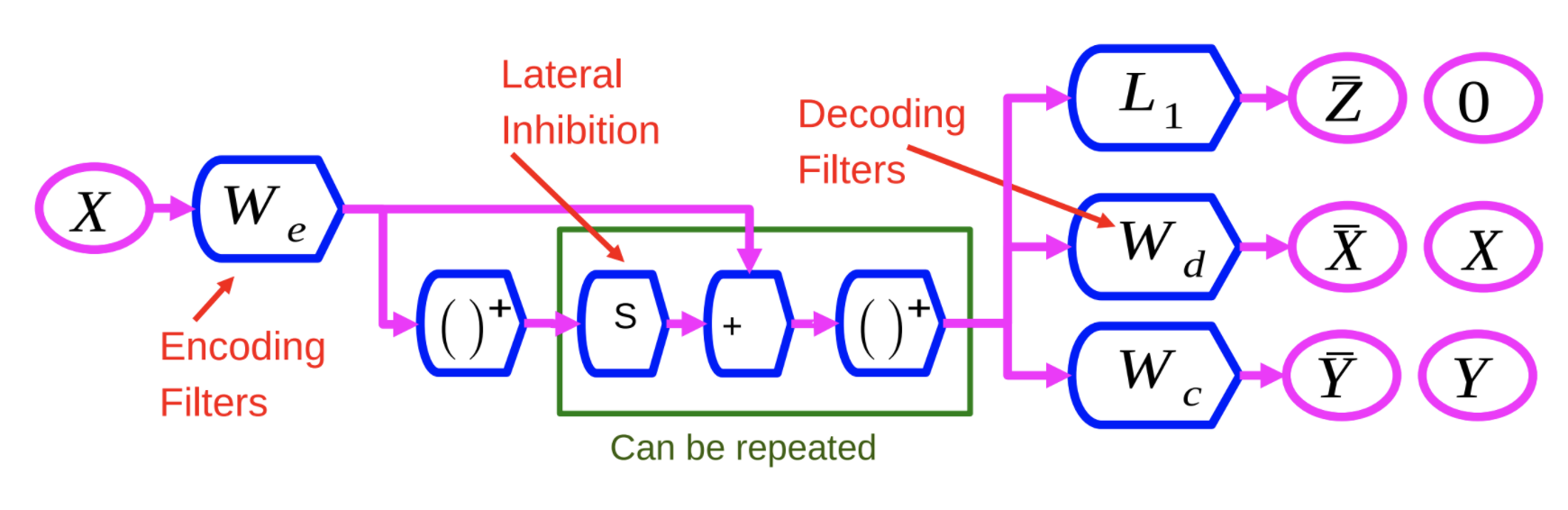
图1：判别类循环稀疏自编码器模型结构

DrSAE的编码器$W_e$ 与LISTA算法里面的编码器相似。输入变量$X$ 先经过了编码器$W_e$ 和一层非线性方程，其结果与与一个可调节的变量矩阵$S$ 相乘，再和$W_e$相加，然后再经过一层非线性方程。这个流程可以被多次重复，每一次相当于网络里面的一层结构。

我们用三个准则来训练这个神经网络：

1. $L_1$: 通过$L_1$范数正则化来产生稀疏隐变量 $Z$。
2. 重建$X$: 通过解码器$W_d$产生与输入变量相似的输出变量。我们用$L_2$损失函数来训练解码器$W_d$
3. 引入第三变量$W_c$：通过训练一个简单线性分类模型$W_c$来预测类别

我们通过同时最小化以上三个准则来训练DrSAE。这样的好处是可以找到能重建输入变量的稀疏隐变量，让神经网络学习到信息含量丰富的隐变量。

组稀疏

组稀疏的核心理念是学习到池化后的稀疏特征，而不是单纯通过卷积后的稀疏特征

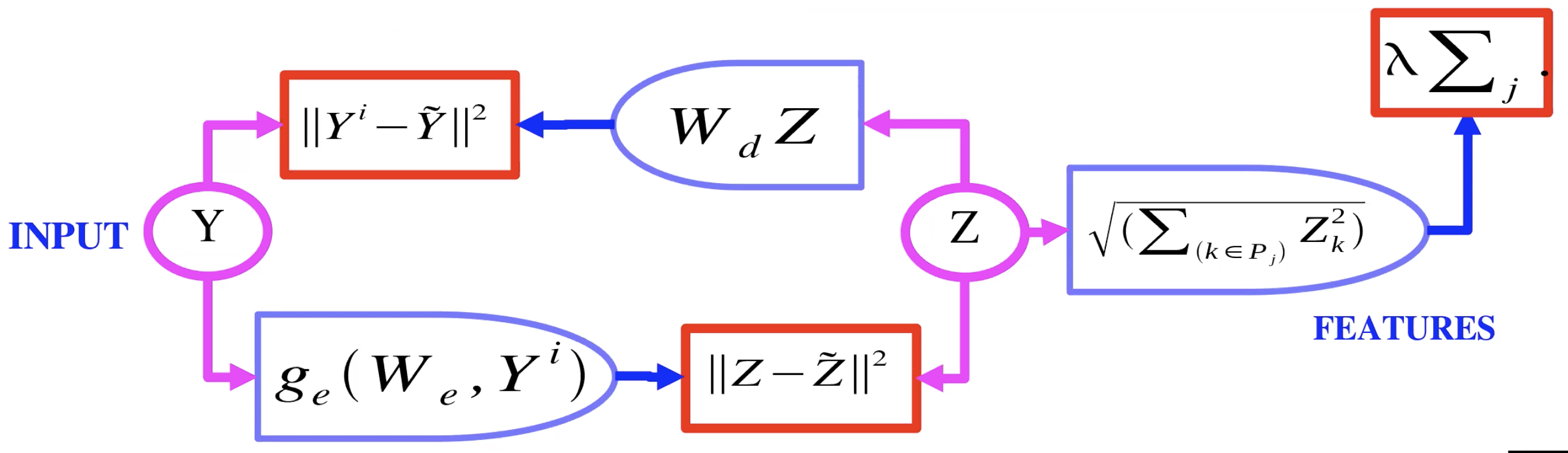
图2：组稀疏自编码器模型结构

图2详细描述了组稀疏自编码器的模型结构。与图1DrSAE的主要分别是对隐变量$Z$ 的正则化：DrSAE使用了$L_1$正则化，而组稀疏对隐变量$Z$每组使用了$L_2$正则化，再将各个组正则化的惩罚因子相加。这样一来，我们可以学习到稀疏的组别（某些组特征的权重变为0），而每组里面通常包含相似的特征。

组稀疏自编码器的问与答

问：图1的策略可不可以用于VAE模型呢？

答：VAE是通过加noise和控制noise的变动来限制隐含量，以防止模型学习到一个无意义的恒等函数。

问：在幻灯片”AE with Group Sparsity”页面（图2），$P_j$ 代表什么？

答：$P_j$是第$j$组，每组含有一群特征。如果$Z$是一维度的向量，我们会把某些元素分类组合起来。一个元素可以同时被分到不同组（组间有元素重叠）。如果$Z$是二维度的图像($\R^{n \times n}$)，那组可以是其中一个二维子集（$\R^{d \times d}, d<n$). 如果$Z$是三维度的立方体，我们可以把它展开变成一个树形图（每个节点/每条边是原来立方体的顶点/边），每个子树是一个组。

问：解释特征池化(feature pooling)

答：编码器产生了隐变量$Z$，然后通过$L_2$正则化组特征，最后经过解码器来重建输入变量（比如图像）。

问：组稀疏可以帮助归类相似的特征吗？

答：不一定。组稀疏的研究是在算力和大数据时代到来之前，目前尚未有大数据实验来得出确切结论。

图像级别训练，无权重分享(weight sharing)的局域过滤器 (local filters)

用无权重分享的局域过滤器来进行图像级别训练未必有效果。这个设计通常是用于图像复原或是无监督学习，并且适用于非常小的数据。网络结构包含卷积编码器和卷积解码器，然后用组稀疏的准则来进行预训练 (pretrain)。当预训练完成后，我们只保留网络的编码器，把它放到目标网络中（通常为第一层）当作一个特征提取器，然后再在它之上添加新的网络层。

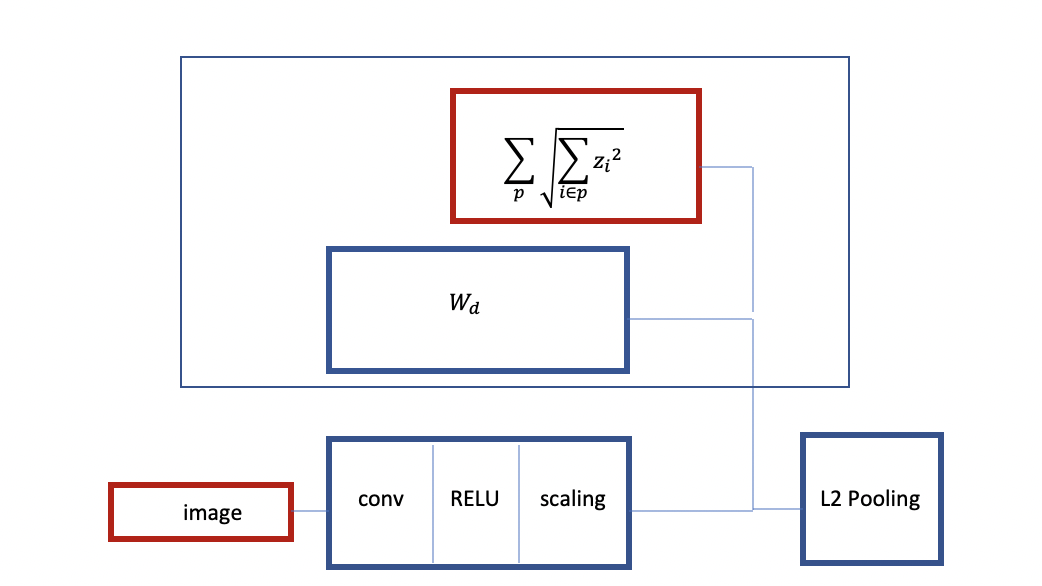
图像3：组稀疏的卷积RELU结构

图3描述组稀疏的卷积RELU结构。图像输入网络后会经过编码器（卷积RELU，缩放层），再经过解码器（线性）。整个网络用重建输入变量以及组稀疏正则化的准则来训练。

这个基础结构可以延伸至更多隐藏层：当训练完图3的一层卷积RELU自编码器后，我们可以把训练好的解码器 $W_d$ 和 $L_2$ 正则化隐变量$Z$ 结合起来当作一层$L_2$ 池化层 (Pooling Layer)。这样一来，网络可以通过编码器和$L_2$ 池化层来提取输入图像的特征。我们可以用提取的特征当作输入变量进而训练一个新的组稀疏卷积自编码器实例(instance)。然后我们把新的组稀疏卷积自编码器叠加到原来的自编码器之上。这样可以预训练一个两层（多层）卷积网络，也被称作堆叠自编码器 (Stacked Autoencoder)。其好处是能够通过组稀疏学习到不变特征。

问：您之前提到可以将隐变量理解成一个树形图，并用其子树来当作组。请问是用所有子树吗？

答：这由你来决定。你可以试验不同大小的子树。我们可以先训练大的子树然后减免掉很少用到的分支。

图4: 图像级别训练，无权重分享(weight sharing)的局域过滤器 (local filters)

图4展示的是用图像级别训练得到的风车模式 (pin-wheel pattern)。注意此处并没有权重分享，网络学习到的是局域性的过滤器。有趣之处在于，在图中红点位置，特征的方向会连续的变换。神经学家观察到了人类大脑有相似的图像模式。

问：请问组稀疏的因子是不是会被训练而得到一个小的数值？

答：组稀疏是一个正则化准则，这个因子不是训练得到的而是固定的。归根结底，这只是组的$L2$ 范数（组是提前决定的）。组稀疏准则会帮助训练编码器和解码器，来控制自编码器学习到的特征。

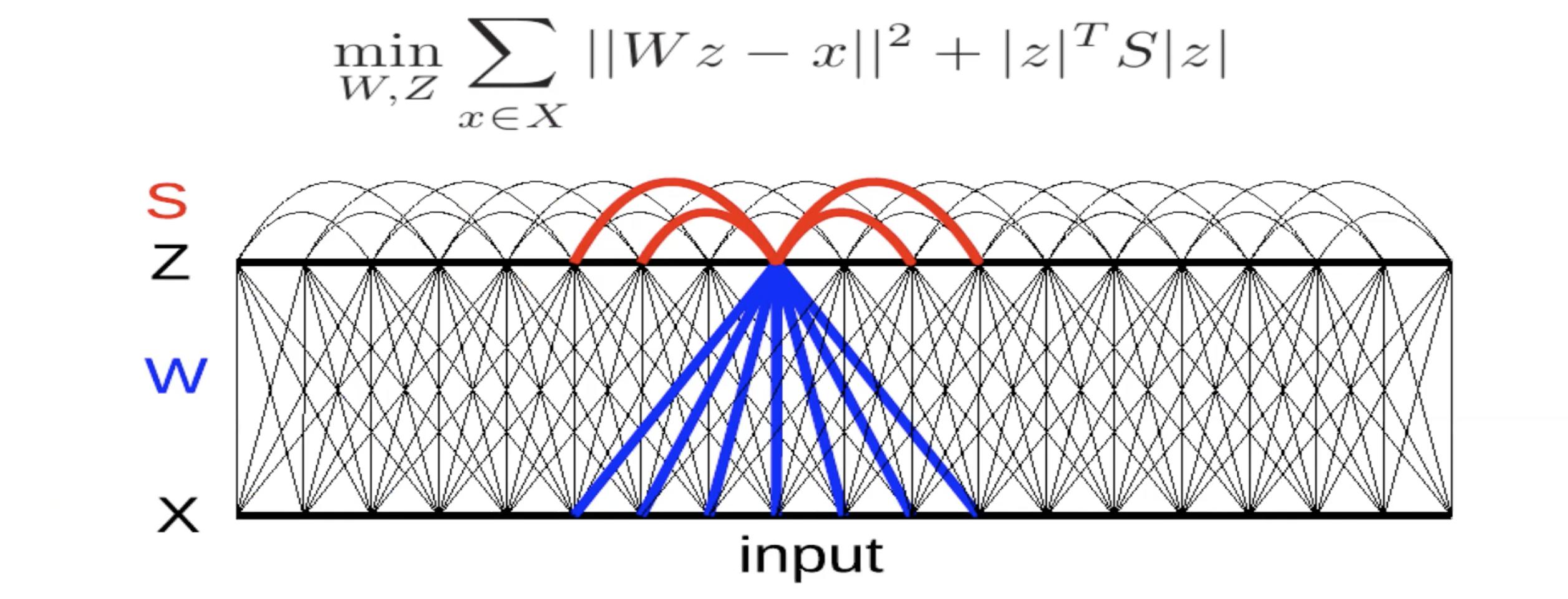
图5: 通过侧向抑制作用提取不变特征

图5展示的是用$L2$损失函数(重构误差)来训练一个线性解码器的自编码器。注意到在目标函数中我们增加了一个准则 $\left\lvert z \right\rvert^T S \left\lvert z \right\rvert$ 。这里的$S$ 可以是提前决定或是训练得到的，并用于最大化这个准则。如果$S$ 的元素是正数并且数值很大，那这个网络会学习到不能让$z_i, z_j$ 同时不为零。这样代表了一种相互抑制作用，在神经学里被称做自然抑制。

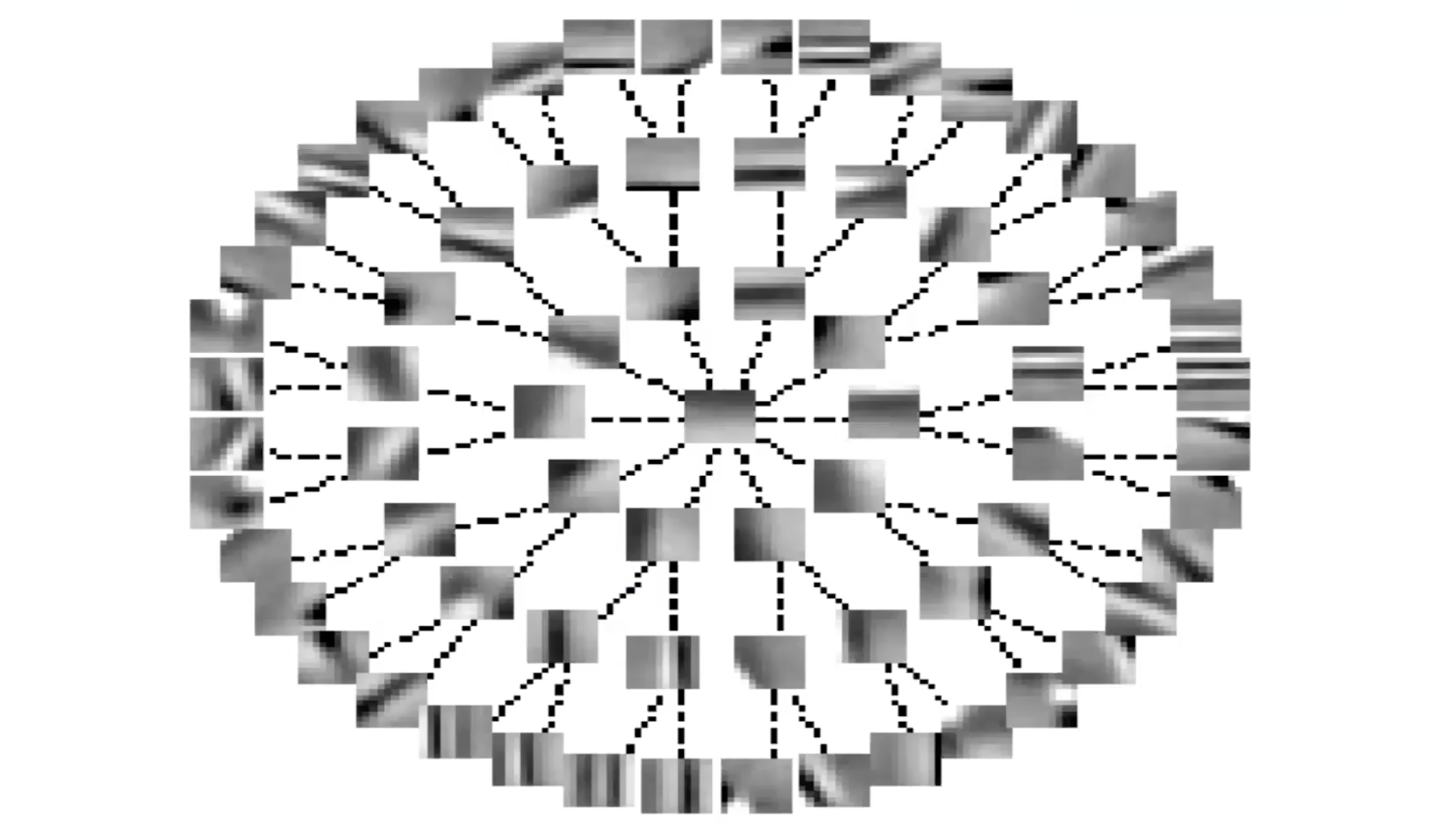
图6: 通过侧向抑制作用提取不变特征（树形图）

如果你把$S$ 矩阵重构成一个树形图，每个边代表着$S$ 数值为0的元素（图6）。如果树中的两个节点之间没有连接，这代表相应的$S$ 元素不为零。由此可见，每个特征会抑制除了其子树上的特征以外的其他所有特征。这个构造可以被看作组稀疏的反例。

你还可以观察到通过这样网络学习到的特征会被排列成一个近似连续不断的结构。在同一个树枝上的特征代表了某种特征的不同方面。特征与其附近特征非常相似，因为它们之间没有抑制作用。

那么我们如何训练这个网络呢？在每一个迭代，通过输入变量$x$，网络尝试找到$z$来最小化这个图5的训练目标方程。然后通过梯度下降来更新$W$，以及梯度上升来更新$S$ （如果我们想训练$S$并让其数值变大 ）。