Generative Models - Variational Autoencoders

回顾: 自编码器（Auto-encoder，AE）

总结一下AE的最简形式：

• 首先，AE通过一个仿射变换（affine transformation）将输入映射到隐藏状态：$\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$，其中$f$是一个一一对应的激活函数。这是编码（encoder）阶段。$\boldsymbol{h}$也称作代码（code）。

• 其次，$\hat{\boldsymbol{x}} = g(\boldsymbol{W}_x \boldsymbol{h} + \boldsymbol{b}_x)$，其中$g$是激活函数。这是解码（decoder）阶段。

• 详细解释请参考笔记：第七周.*

VAE的直观理解与经典AE的比较

接下来，我们介绍了变分自编码器（Variational Autoencoders，VAE），它是一种生成模型（generative model）。为什么我们要关心生成模型呢？首先我们要了解，判别模型（discriminative model）是学习从给出的观察中做出预测，而生成模型要模拟数据生成的过程。所以生成模型可以更好地理解因果关系，从而有更好的泛化（generalization）。

注意，虽然VAE名字里包含了AE（因为架构相似），但是VAE和AE的构想有很多不同，如图1所示。

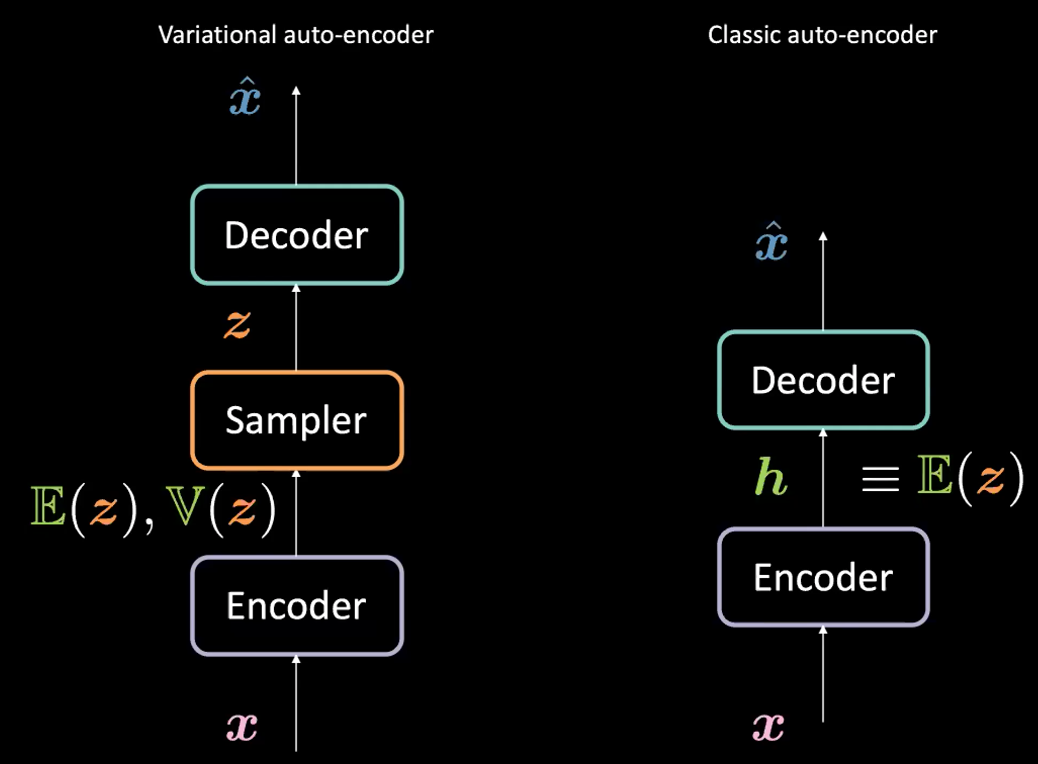
图1: VAE vs. 经典AE

VAE与经典AE之间的区别

VAE：

• 第一步，编码阶段：将输入$\boldsymbol{x}$传送到编码器。VAE的代码由两种东西构成：一种是$\mathbb{E}(\boldsymbol{z})$，另一种是 $\mathbb{V}(\boldsymbol{z})$。$\boldsymbol{z}$是一个隐随机变量，它遵循高斯分布，其平均数为$\mathbb{E}(\boldsymbol{z})$、方差为$\mathbb{V}(\boldsymbol{z})$。注意，在实际应用中，人们用高斯分布作为编码分布，但是也可以用其他的分布。

  • 编码器是一个从$\mathcal{X}$映射到$\mathbb{R}^{2d}$的函数：$\boldsymbol{x} \mapsto \boldsymbol{h}$（此处我们用$\boldsymbol{h}$表示$\mathbb{E}(\boldsymbol{z})$ 和$\mathbb{V}(\boldsymbol{z})$之间的联系）。

• 其次，我们通过上述被编码器参数化的分布对$\boldsymbol{z}$采样。具体讲就是$\mathbb{E}(\boldsymbol{z})$和$\mathbb{V}(\boldsymbol{z})$被传送进一个采样器（sampler）生成隐函数$\boldsymbol{z}$。

• 然后，$\boldsymbol{z}$被传送进解码器生成$\hat{\boldsymbol{x}}$。

  • 解码器是一个从$\mathcal{Z}$映射到$\mathbb{R}^{n}$的函数：$\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$。

其实，对于经典AE，我们可以将$\boldsymbol{h}$看作VAE形成里的向量$\E(\boldsymbol{z})$。简单来讲，VAE和AE之间的主要区别是VAE有一个潜在空间可以启用生成过程。

VAE的目标（损失）函数

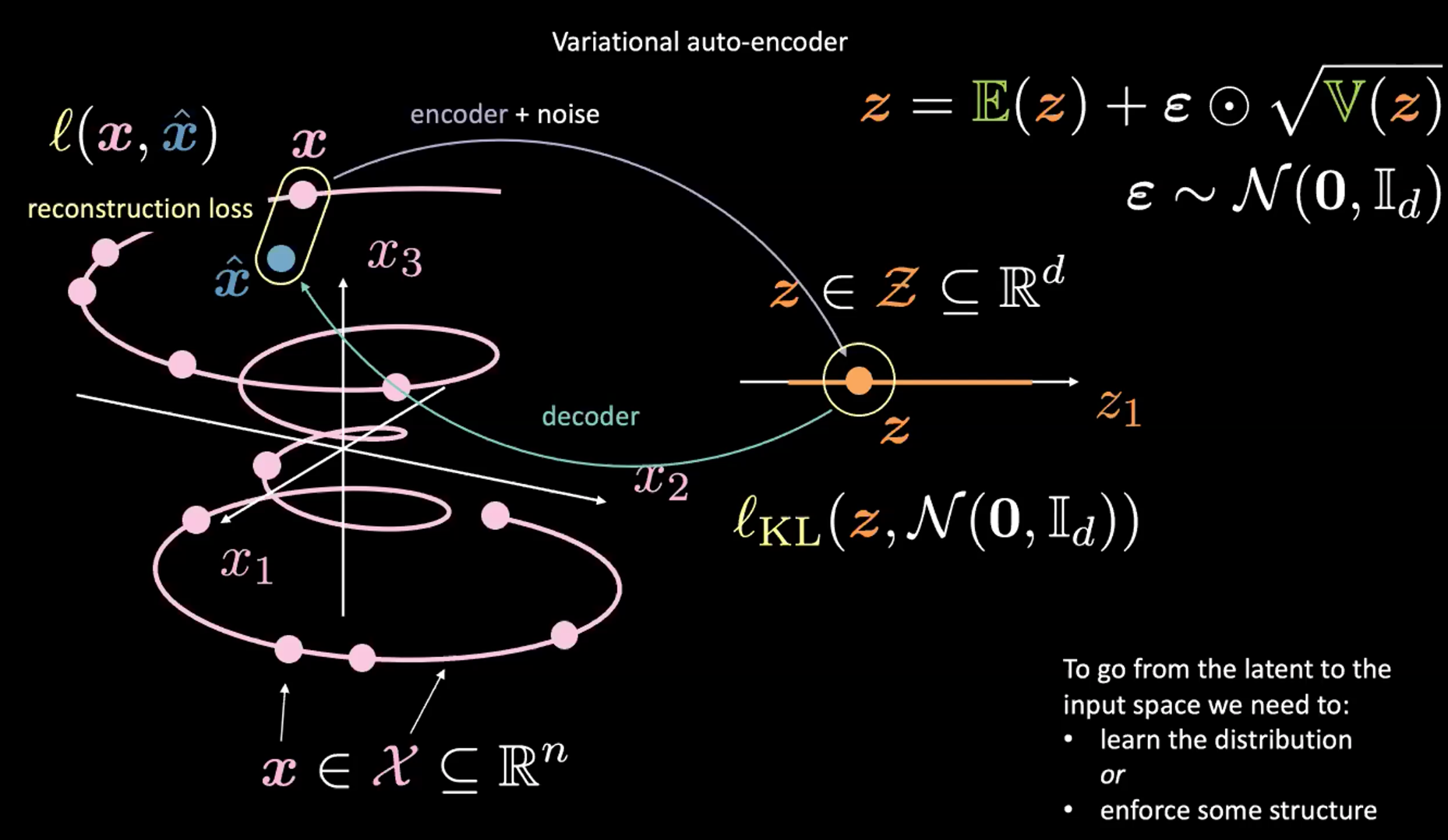
图2: 输入空间到潜在空间到映射

见图2。暂时忽略右上角（重参数技巧，详见下一节）

首先，我们通过编码器和噪声将输入空间（图左）编译至潜在空间（图右）。然后，我们从潜在空间（图右）解码到输出空间（图左）。从潜在空间到输入空间（生成过程）需要学习数据（或潜在代码的）分布，或者强迫形成某种结构。这里，VAE迫使潜在空间形成某种结构。

和通常一样，我们最小化损失函数来训练VAE。损失函数由一个重构因子（Reconstruction Term）和一个正则化因子（Regularization Term）组成。

• 最后一层的重建因子（图左），对应的是图中的$l(\boldsymbol{x}, \hat{\boldsymbol{x}})$ 。

• 正则化因子在隐藏层中，它是为了迫使隐藏空间（图右）形成某种高斯分布结构。我们用一个惩罚因子 $l_{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d))$来完成。没有了这一项，VAE就像一个经典AE一样，会造成过拟合，而且会失去我们想要的生成性质。

$\boldsymbol{z}$采样的讨论（重参数技巧（Reparameterization Trick））

我们如何对VAE中被编码的分布进行采样？如上所述，为了取得$\boldsymbol{z}$，我们从高斯分布中采样。然而，这么做的问题是，当我们用梯度下降训练VAE模型时，我们不知道该如何通过采样部分做向后传播。

我们用重参数技巧来“采样”$\boldsymbol{z}$。我们用$\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$，其中$\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$。这种情况下就可以在训练中使用向后传播。具体来讲，梯度会经过上述式子里的一一对应相乘和相加。

详解VAE损失函数

可视化预测隐变量（Latent Variable）与重构损失函数

如上所述，VAE的损失函数有两个部分：一个重构因子和一个正则化因子。我们可以将其写作： \(l(\boldsymbol{x}, \hat{\boldsymbol{x}}) = l_{reconstruction} + \beta l_{\text{KL}}(\boldsymbol{z},\mathcal{N}(\textbf{0}, \boldsymbol{I}_d))\)

要想象损失函数里的每一项的用意，我们可以将每一个估计的$\boldsymbol{z}$想成一个二维空间里的圆圈，圆心是$\mathbb{E}(\boldsymbol{z})$。圆内周围的区域是$\boldsymbol{z}$的可能的值，它取决于$\mathbb{V}(\boldsymbol{z})。

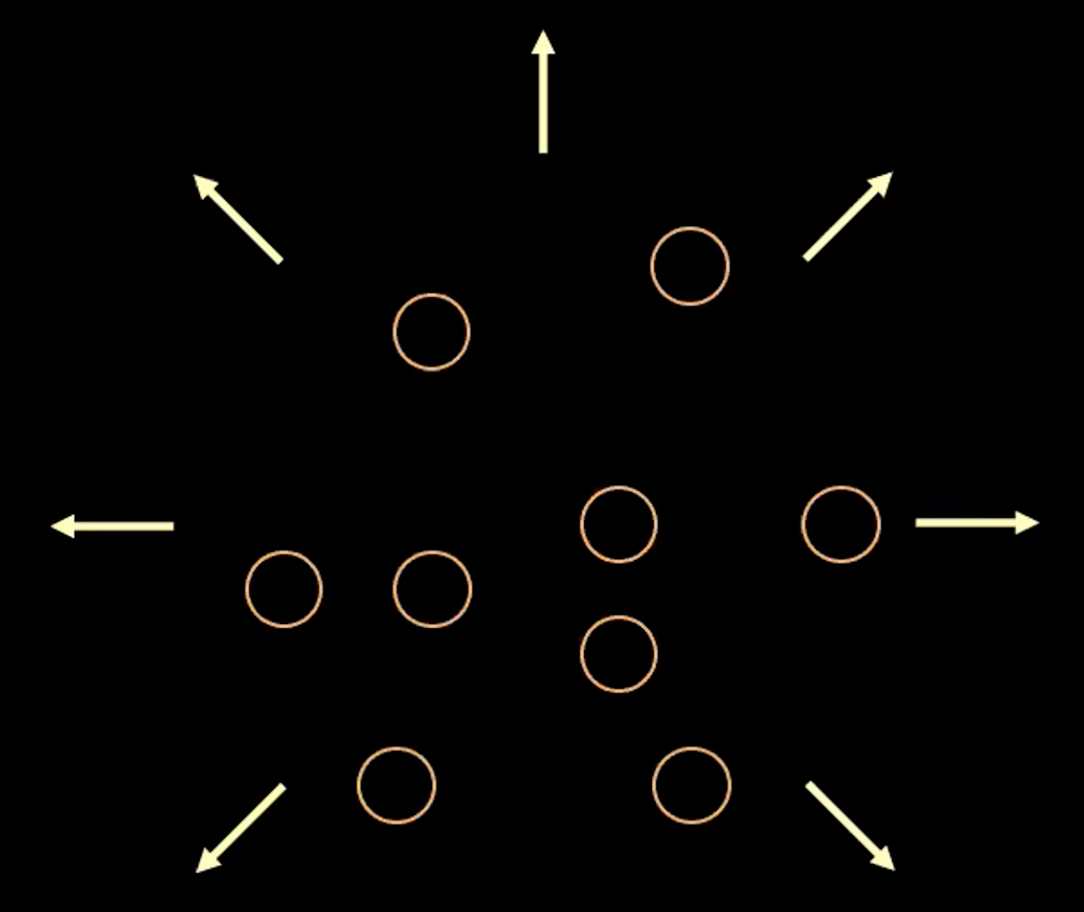
图3: 隐藏层里的向量z可视化成的泡泡

如图三所示，每个泡泡代表一个$\boldsymbol{z}$的估计区域。箭头代表了重构因子将每个估计值从彼此之间推开，下面是详细解释。

如果任意两个的$z$估值之间有重叠（两个泡泡相互重叠），这会对重构造成干扰，因为重叠的点回映射到同一个原始输入。所以重构损失函数会将点和点推开。

然而，如果我们只用重构损失函数，估测值会持续将彼此推远，系统就会爆炸。这时就需要用到惩罚因子。

注：二元输入（Binary Input）的重构损失函数为： \(l(\boldsymbol{x}, \hat{\boldsymbol{x}}) = - \sum\limits_{i=1}^n [x_i \log{(\hat{x_i})} + (1 - x_i)\log{(1-\hat{x_i})}]\)

实输入（Real-valued Input）的重构损失函数为： \(l(\boldsymbol{x}, \hat{\boldsymbol{x}}) = \frac{1}{2} \Vert\boldsymbol{x} - \hat{\boldsymbol{x}} \Vert^2\)

惩罚因子（Penalty Term）

第二项是$\boldsymbol{z}$之间的相对熵（Relative Entropy，是两个分布之间的距离的测量），其来源于高斯分布，平均值是$\mathbb{E}(\boldsymbol{z})$，方差是 $\mathbb{V}(\boldsymbol{z})$。我们将VAE损失函数的第二项展开可得： \(\beta l_{\text{KL}}(\boldsymbol{z},\mathcal{N}(\textbf{0}, \boldsymbol{I}_d)) = \frac{\beta}{2} \sum\limits_{i=1}^d(\mathbb{V}(z_i) - \log{[\mathbb{V}(z_i)]} - 1 + \mathbb{E}(z_i)^2)\)

其中，和的每一步有四项。我们在下方写出第一项，并在图4画出后面三项。 \(v_i = \mathbb{V}(z_i) - \log{[\mathbb{V}(z_i)]} - 1\)

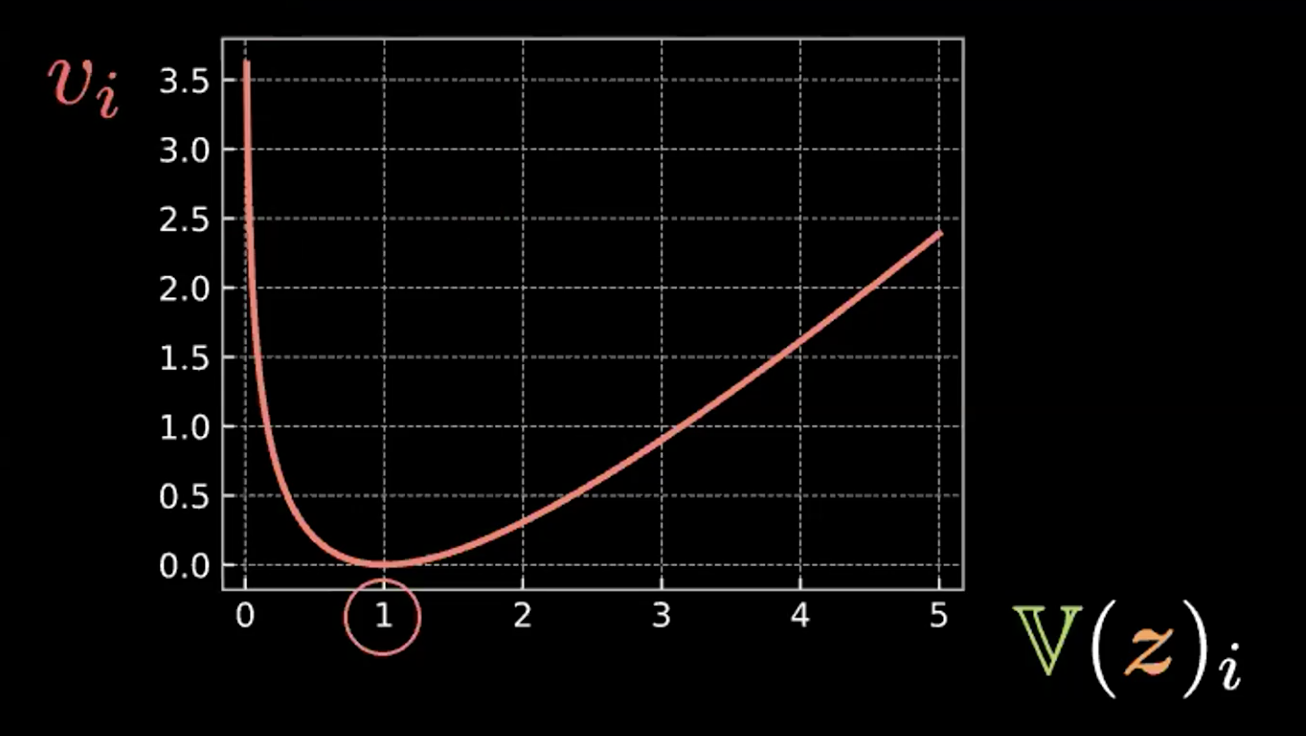
图4: 图示相对熵如何迫使“泡泡”的方差为1

可以看到，当方差为1时，表达式到达最小值。所以我们的惩罚损失函数会将估测的隐藏变量的方差保留到约1。想象一下的话，这就意味着上图的“泡泡”的半径约等于1.

最后一项，$\mathbb{E}(z_i)^2$会最小化$z_i$之间的距离，因此预防了重构因子引发的“爆炸”。

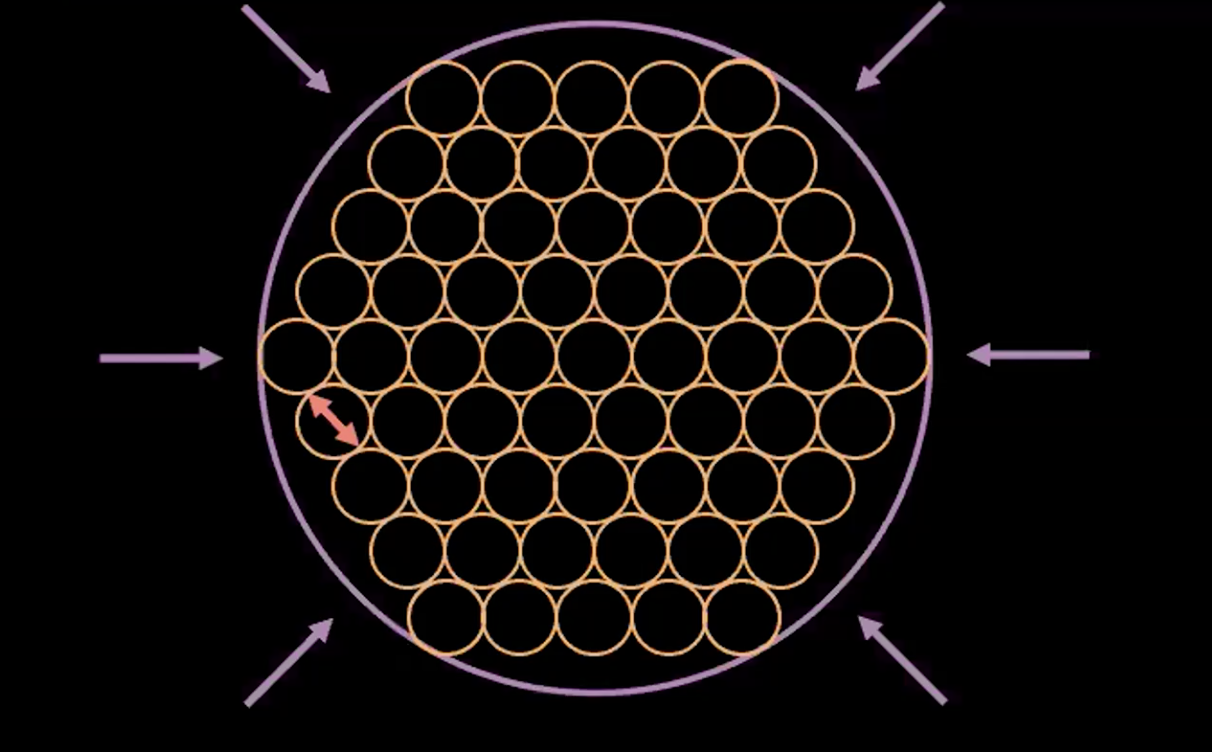
图5: 解释VAE：“泡泡”中的“泡泡”

图5显示了VAE损失函数把估测的隐藏变量之间挤压而不造成重叠，且同时使每个点的估测方差维持在1。

注：VAE损失函数中的$\beta$是一个超参数（Hyperparameter），它用来决定重构因子和惩罚因子之间的权重。

VAE的实现

Jupyter Notebook在这里。

在这个笔记里，我们执行了VAE并在MNIST数据集对它进行训练。然后我们从一个正态分布里对$\boldsymbol{z}$进行采样，并且将它输送到解码器里比较结果。最后，我们观察$\boldsymbol{z}$在二维投影里如何变化。

注： 在我们用到的MNIST数据集中，像素值已经被归一化到$[0, 1]$的区间。

编码与解码

1. 我们在VAE模块中定义编码器和解码器。

2. 在编码器的最后一个线性层，我们定义输的大小为$2d$，前一半的值为平均值，剩下一半的值为方差。我们用这些平均值和方差对$\boldsymbol{z} \in R^d$采样，用以解释之前的重参数技巧。

3. 对于编码器的最后一个线性层，我们用Sigmoid激活函数，便于使输出集中在$[0, 1]$之间，和输入数据类似。

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

重参数与forward函数

对于reparameterise函数，如果模型在训练模式下，我们从log方差（logvar）中计算标准偏差（std）。我们用log方差而不是普通的方差，因为我们想要使方差为非负的，对其求log可以保证我们有方差的全部值域，这样可以试训练更加稳定。

在训练过程中，reparameterise方程做出重参数技巧以便于我们可以在训练中做向后传播。如讲座中所解释，为了与黄色泡泡的概念连接起来，每次这个方程式被召唤后，我们会画一个点eps = std.data.new(std.size()).normal_()。如果我们重复100次，我们可以得到100个点，这样会大致形成一个球，因为这是一个正态分布。而且eps.mul(std).add_(mu)使这个球以mu为圆心、以std为半径。

对forward方程，我们先从编码器中计算mu（前一半）和logvar（后一半），然后我们通过reparamterise方程计算$\boldsymbol{z}$。最后，我们return解码器的输出。

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        eps = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

VAE的损失函数

这里我们定义重构损失函数（二元交叉熵，binary cross entropy）和相对熵（KL散度熵，KL Divergence Penalty）。

def loss_function(x_hat, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + KLD

生成新的样本

在我们训练完模型之后，我们可以从正态分布里抽取一个随机的$z$并把它输送到解码器。我们可以观察图6，其中一些结果不太理想，因为我们的解码器没有“覆盖”整个隐藏空间。我们可以通过增加训练周期来提升结果。

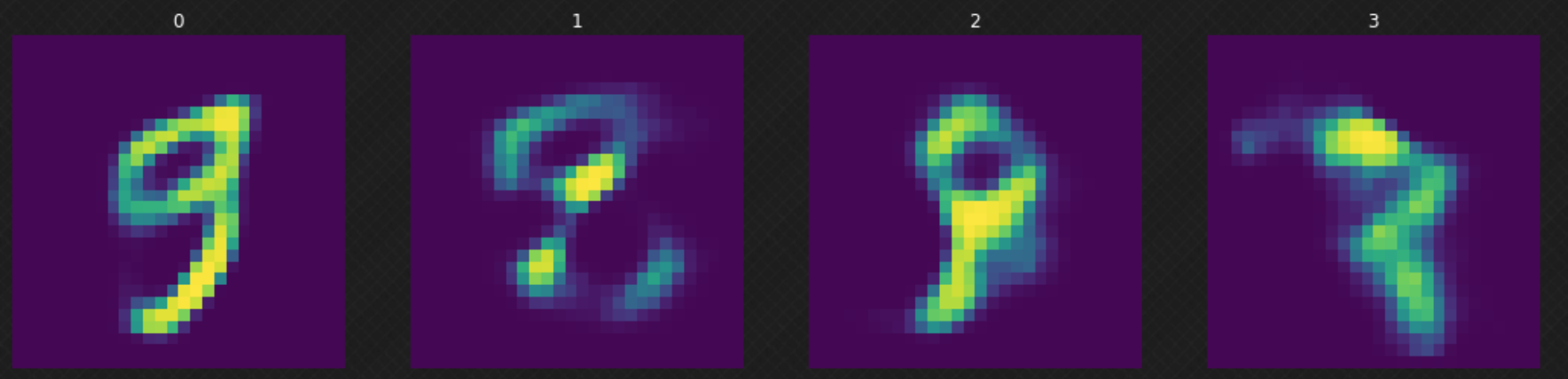
图6: 在隐藏层里随机移动

我们可以观察一个数字如何变形成另一个，而这用AE是不能可完成的。可以看到当我们在隐藏空间里漫步时，解码器的输出看起来任然完好。图7展示了我们如何是数字$3$变形至数字$8$。

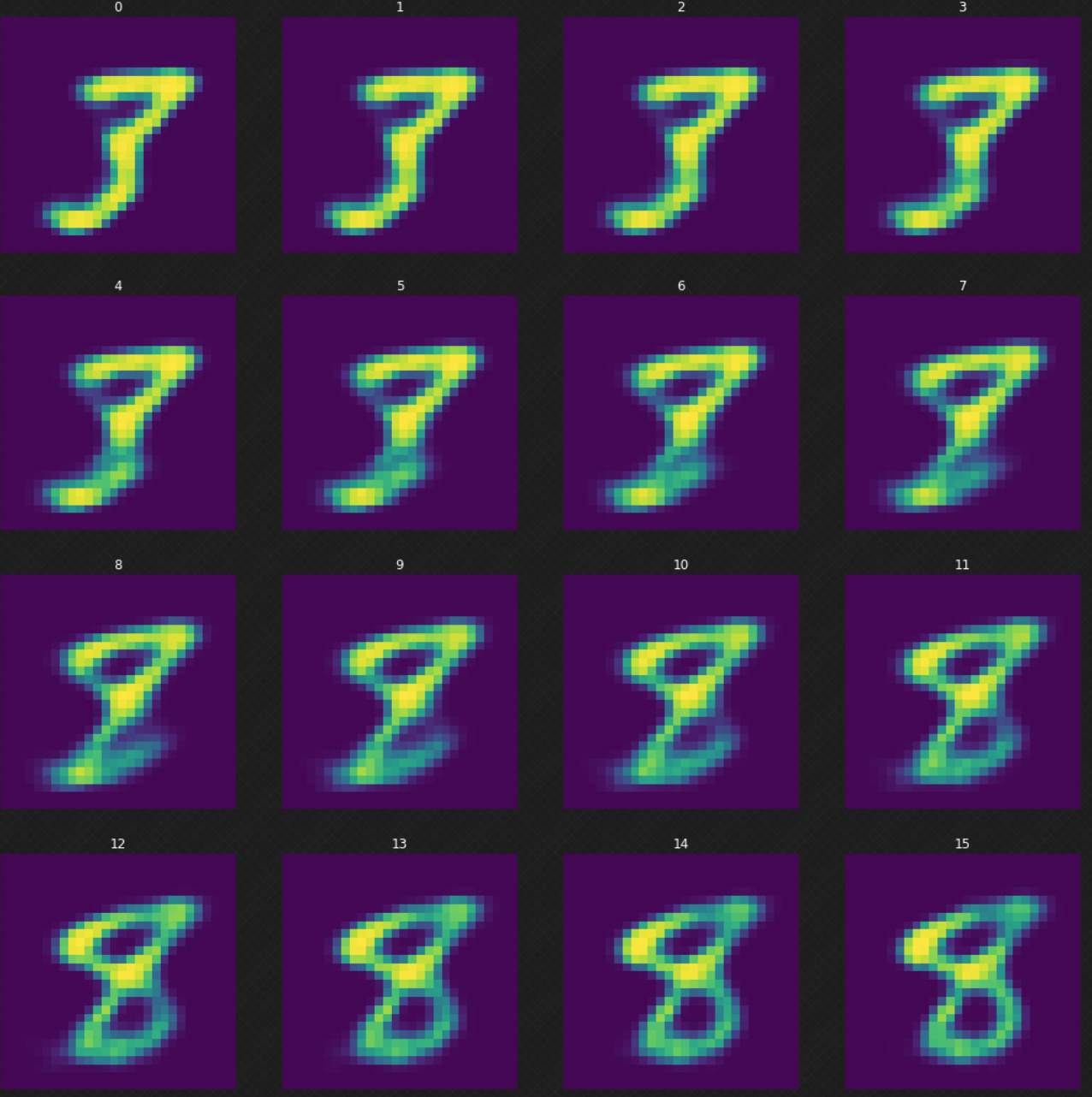
图7: 数字3到数字8的变形

平均数的投影

最后，我们来观察隐藏层在训练中/训练后是如何变化的。图8中的图表是从编码器输出的平均值，投射在一个二维空间上，每个颜色代表一个数字。可以看到从周期0开始，数字的类别分布得很散，几乎没有各自的聚集。当模型开始被训练后，隐藏空间逐渐变得定义明确（well-defined），并且数字开始形成聚类。

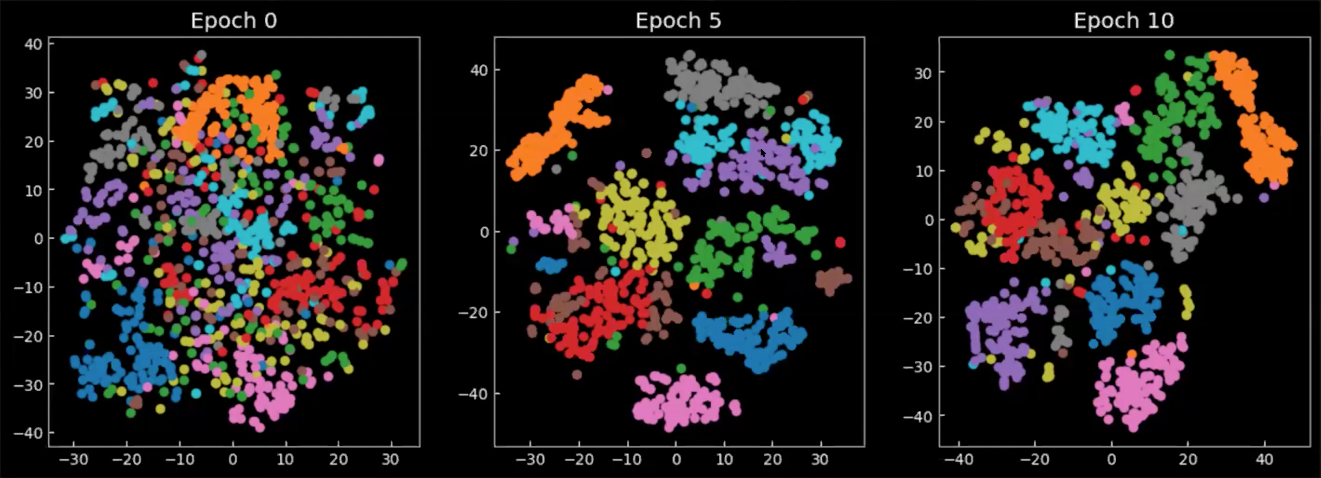
Fig. 8: 在隐藏空间中的平均值$\E(\vect{z})$的二维投影