正则化潜变量能量基礎模型

正则化潜变量能量基礎模型

具有潜在变量的模型能够生成预测分布 $\overline{y}$，這分佈是基于观察输入$x$和附加上的潜在变量$z$所生成的。 基于能量基礎模型还可以包含潜在变量:

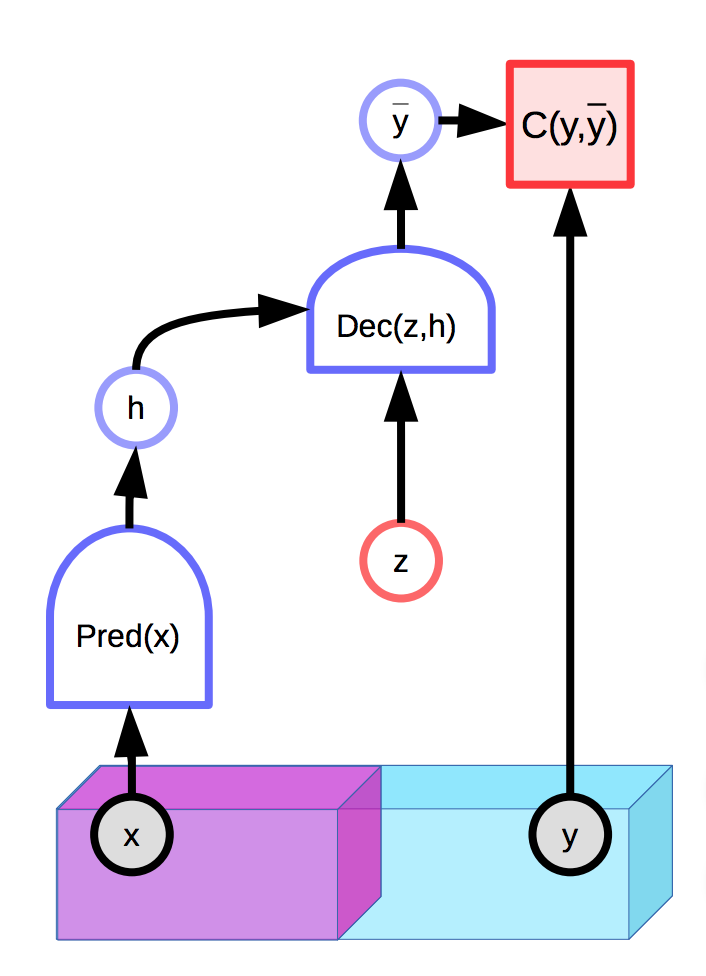
图1: 具有潜在变量的能量基础模型的示例

请看之前的讲座笔记来了解更多的细节。

不幸地，如果潜在变量$z$在生成最后的预测输出$\overline{y}$中有太多表达力或影响力，那在适当的选择$z$后，输入$x$会完美地重建回应有的形态，也就是每一个正是的输出$\overline{y}$。这是说出当能量函数在所有地方都是0，因为能量会在推理中在$y$和$z$上被优化。

一个自然的解决方法是限制潜在变量$z$的信息容量。其中一个做法是正则化潜在变量：

这个方法会限制空间$z$的容量，也就会选一个细小的值和这些个会反过来控制$y$空间中只有小能量的地方，而这个Lambda的值会控制这个限制行为。一个有用的$R$的例子是$L_1$规范，也就是在一个有效的维度下，所有地方都是可以可微和近似的。在限制它的$L_2$规范时对$z$加上噪声的话，那就能限制它的信息内容(VAE)。

稀疏编码

稀疏编码是一个无条件正规化潜在变量式能量基础模型，也就是本质上是尝试去用一个分段线性函数对数据进行近似。

$n$维度向量$z$会有一个非零分量的最大的数字$m « n$。而每一个$W$z会是$W$的列中$m$的扩张中的部份。

在每个优化步骤之后，在$W$的列以$L_2$规范式来加起来后，矩阵$W$和潜在变量$z$就会被归一化。这确保$W$和$z$没有发散到无限和0。

FISTA

图2:FISTA计算图

FISTA(快速ISTA)是一个算法，它用交替地优化两个项$\Vert y - Wz\Vert^2$ 和 $\lambda \Vert z\Vert_{L^1}$来优化相对于$z$的优化稀疏编码能量函数$E(y,z)$。我们初始化$Z(0)$和根据以下规则来反复地更新$Z$:

当中的部份 $Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$ 是用在 $\Vert y - Wz\Vert^2$ 项的一个梯度步。 这个$\text{缩小}$ 函数之后移动数值到0，也就优化 $\lambda \Vert z\Vert_{L_1}$ 项. Shrinkage:缩小

LISTA

FISTA 用在高维度数据而又大量的集时(比如图片)计算上是很昂贵。一个更有效率的做法是改為训练一个网路去预测最佳的潜在变量$z$:

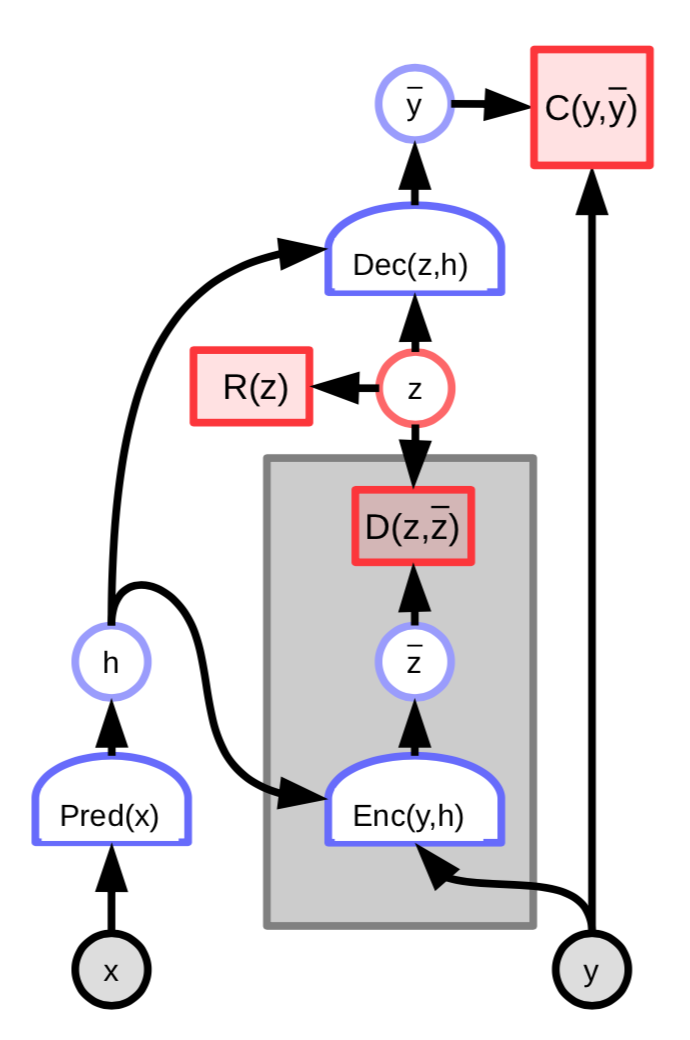
图3: 带有潜在变量编码器的能量基础模型

这个架构的能量就包含了附加项，这附加项会测量预测出来的潜在变量$\overline z$和最佳潜在变量$z$的不同:

我们可以更进一步定义

然后就写

\(z(t+1) = \text{Shrinkage}_{\frac{\lambda}{L}}[W_e^\top y - Sz(t)]\) Shrinkage:缩细

这个更新规则可以被解释为循环网络，也就建议我们改为学习一个参数$W_e$，而它反复地判断潜在变量$z$。网路是以一个固定的时间长度，长度为$K$，这个时间长度和$W_e$的梯度都是用标准的时间上反向传播( standard backpropagation-through-time)。这个训练后的网路会比FISTA算法花费更少的迭代(iteration)生成一个好的$z$。

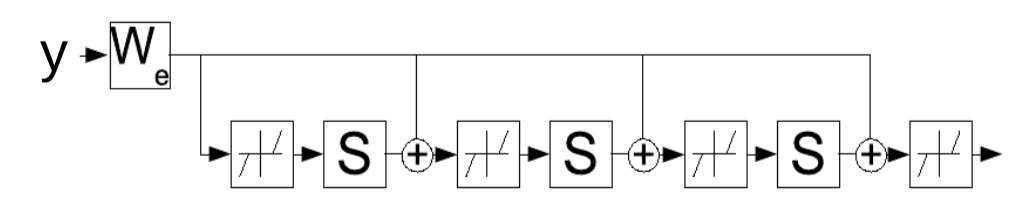
图4: LISTA以一个展开循环网络中的时间点。

稀疏编码示例

当一个有256维度潜在变量向量的稀疏编码系统是用在MNIST手写数字中时，系统就会学到一个256划的集合，它能是线性组合来仿造出训练集(差不多整个训练集)。稀疏正则化器确保它们由很细的数字开始被仿造。

图5: MNIST上的稀疏编码。每一张图都是在W列中学出了东西的。

当稀疏编码被在一些自然图像中用上时，学到的特征就是gabor过滤器，也就是朝向边缘的。这些特征类似于在动物视觉系统早期学习到的特征。

卷积稀疏编码

假设，我们有一个图片和图片的特征图（feature map）($z_1, z_2, \cdots, z_n$)。然后我们能用核心$K_i$来卷积($*$) 每一个特征图。之后就重建造法就能简单的如以下计算出来:

这是跟原本的卷积稀疏编码有点不一样，那个重建造法是以这样来完成的: $Y=\sum_{i}W_iZ_i$。在正常的卷积稀疏编码，我们有一个列的加权和，它的权是$Z_i$的系数。在卷积稀疏编码中，它还是一个线性运算，但字典矩阵现在是一些特征图（feature map）和我们以每一个核心和加起来的结果来卷积每一个特征图。

自然图像上的卷积稀疏编码

图6 获得过滤器和基础函。数线性卷积解码器。

编码器和解码器各自的过滤器都十分相似。解码器人简单地是一个卷积跟着一些非线性，而且一个对角层来改变它的大小。而代码约束上有着稀疏性。解码器只是一个卷积线性解码器和这里的重建是一个平方误差。

所以，如果我们假设只有一个过滤器(filter)，那么它只是一个环绕中央的过滤器。有着四个过滤器，就有一些奇形怪状的过滤器。 4个过滤器，我们得到有方向性的边(水平和垂直);每个过滤器给出2个极性。而8个过滤器，我们就得到八个不同方向性的边。 16个，我们就有更多沿中心出发的方向性物。随着我们继续增加过滤器，我们就有更多类形的过滤器，我们也得到不同方向性的格栅探测器，包括中心周围和其他。

这个现象看上去很有趣，因为它和我们在视觉皮层中观察到的有点像。所以这指示出我们以完全不受监督的方式下能学到很好的特征。

作为附带使用，如果我们用这些特征，然后将它们输入到卷积网中，之后在一些任务上训练它们，那我们不一定有比从头开始训练图像网路的成绩有更好的成绩。相反的，是有些实例表示，它可以帮助提高性能。比如，一旦样本数量不足或太少类别，那样去以纯监督方式进行训练，我们就只有退化了的特征。

图7 在彩色图像上的卷积稀疏编

上方的图是另一个在彩图上的例子。解码核心(右边那个)是9乘9的大小。这核心是被以卷积性地用在整个图片。左图是来自编码器的稀疏代码。而$z$向量空间是十分稀疏的，它只有数个只是白和黑的分量。

可变自动编码器

可变自动编码器的架构是十分相似于正则化潜在变量能量基础模型，但没有其稀疏性。反而，代码的信息内容受噪声的限制

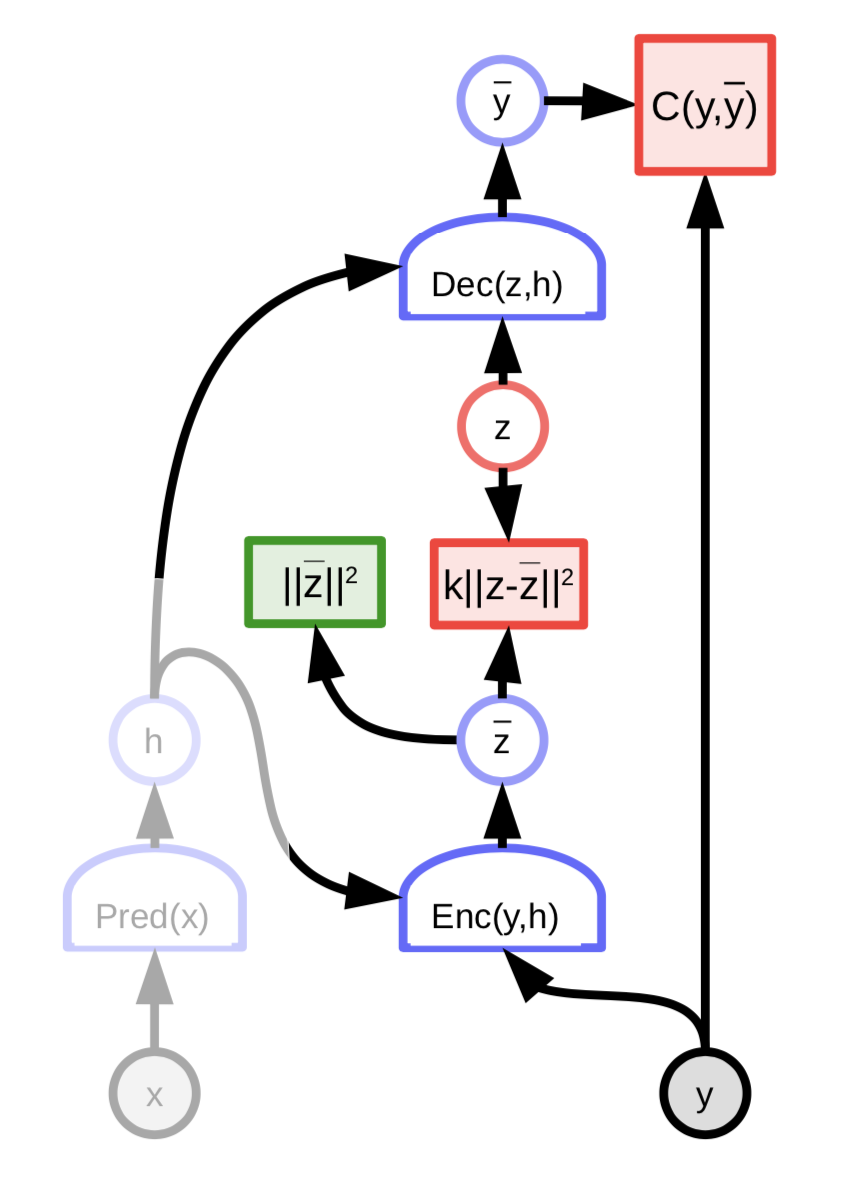
图8: 可变自动编码器的架构

潜在变量z是没有以相对$z$来降低能量函数来被计算出来。反而能量函数被视为是根据一个分布，这个分布的对数就是和${\overline z}$有关系的代价值，然后就是根据这个分布来随机地采样$z$的。这个分布是一个有用上${\overline z}$的平均值的高斯分布，这样就造成出将高斯噪声添加到${\overline z}$上。

这个加上了高斯噪声的代码向量能被看成一些很模糊的球，就如图9(a)。

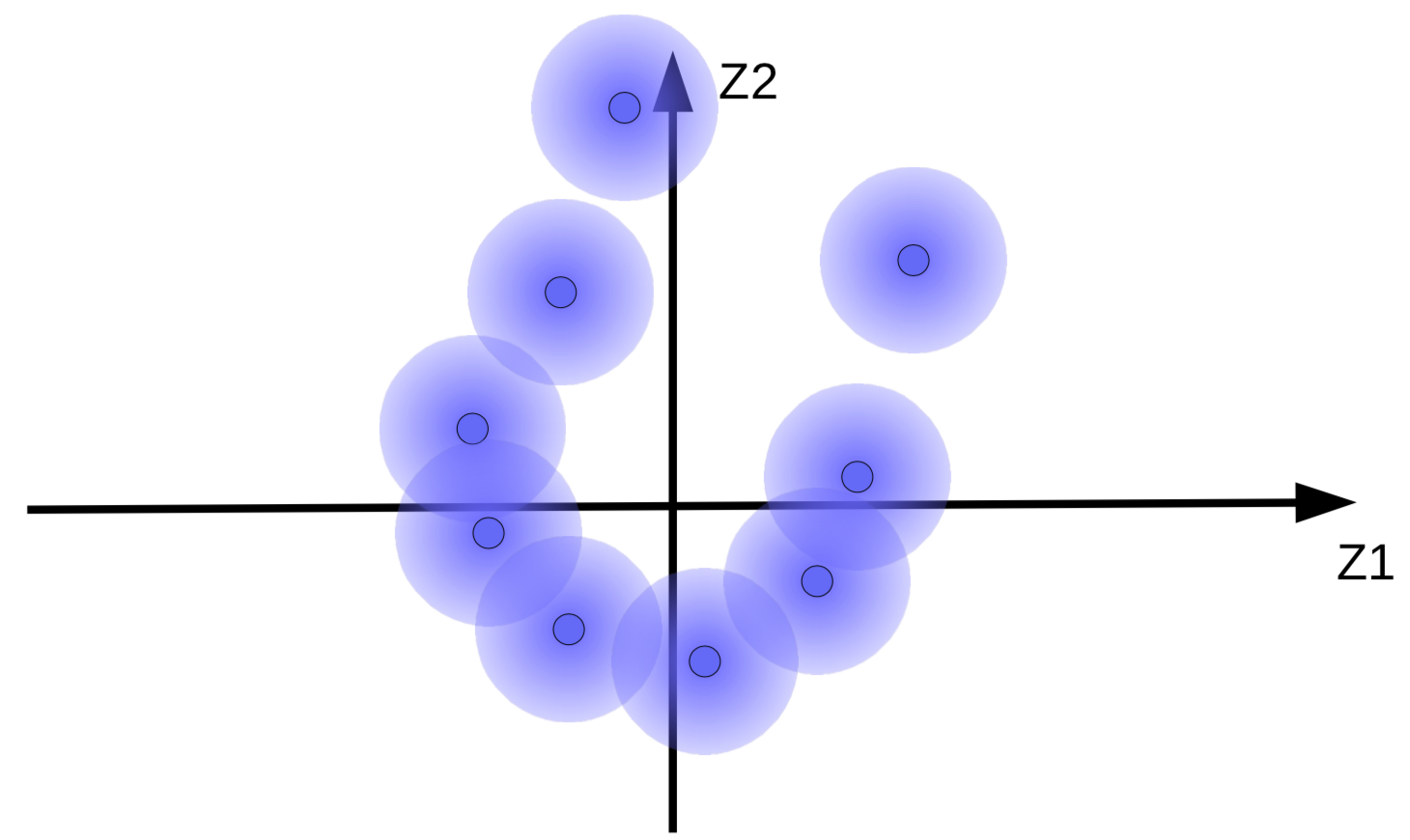(a) 原始的模糊球

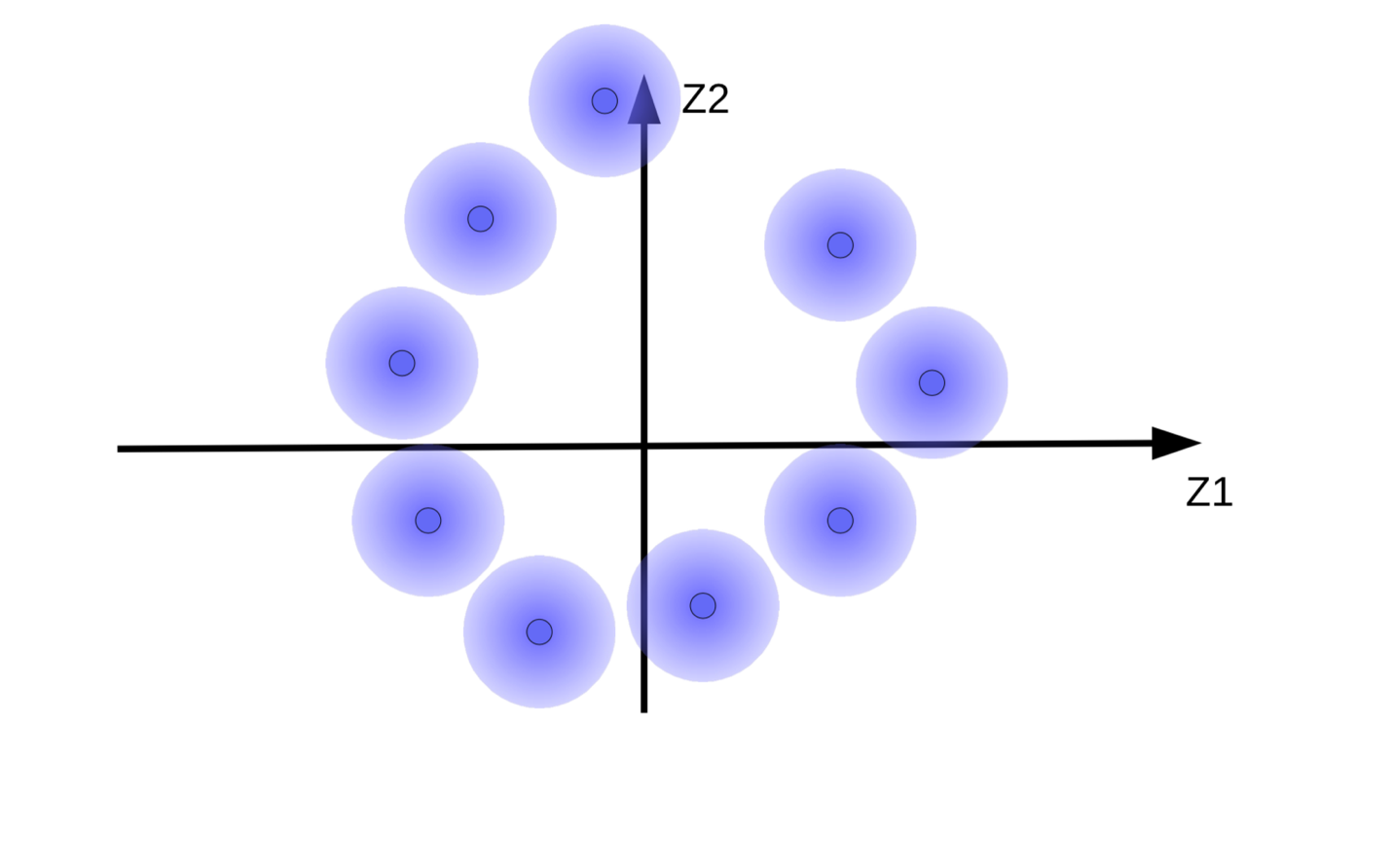(b) 由于没有正则化的能量最小化而导致的球运动

这个系统尝试去令代码向量${\overline z}$有多大得多大，那样$Z$(噪声)就有多细得多细。这结果就是模糊球由起点飘开，就如图9(b)那样。另一个原因为什么系统尝试去令代码向量多大得多大，就是为了防止模糊球重叠起来，也就令解码器对不同的样本进行重建时感到混乱。

但如果我们去令模糊球聚集在数据流形，如果有数据流形的话。所以，代码向量们就会被正规化到只有平均值和方差都接近零。做成这个的话，我们就要用弹簧来把它们连接到起源点，就如图10所示。

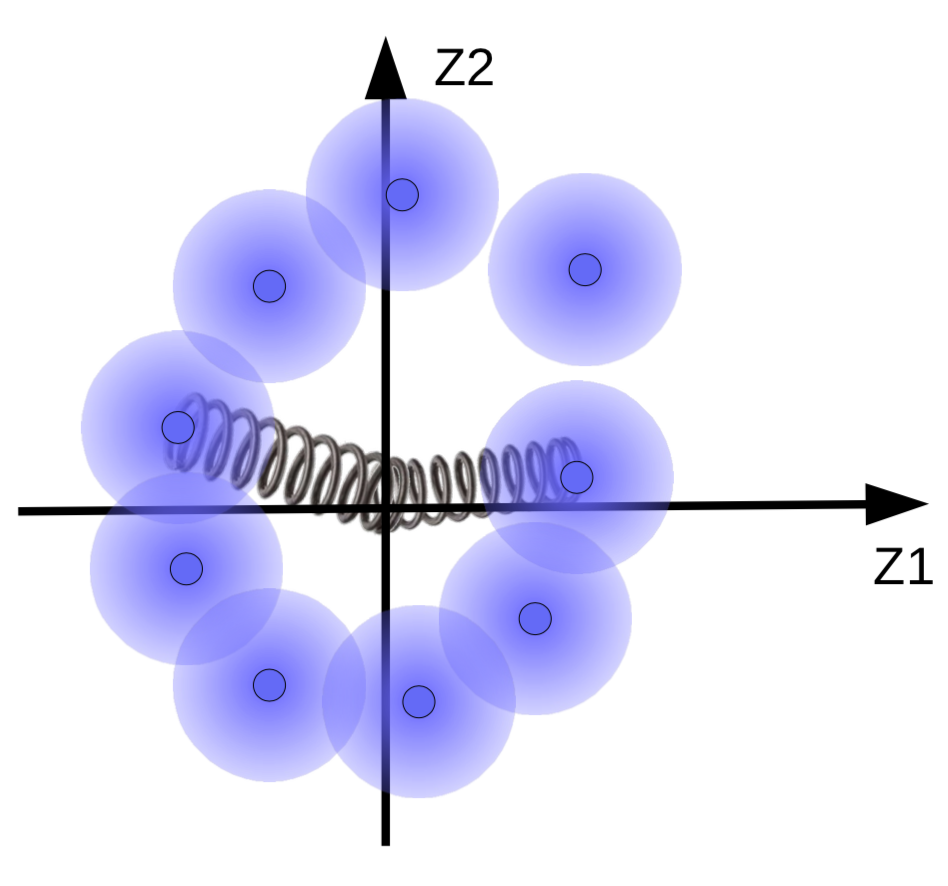
图10: 图像版有弹簧的正则化产生的影响

弹簧的力道决定模糊球有多近起源点。如果弹簧很弱，那模糊球就会由起源点飞开。而如果太强，那它们就在起原点合并起来，导致很高的能量值。为了防止这个的话，系统就只会当相应的样本是相似时，会让球重叠起来。

可能的做法是改写模糊球的大小。惩罚函数会限制这做法，惩罚函数会试图令方差接近1，所以当球合拼起来时，大小既不会太大也不会太小。